狙击步枪弹准静态弹头挤进力研究

刘国庆,徐诚

（南京理工大学机械工程学院,江苏南京 210094）

狙击步枪弹准静态弹头挤进力研究

刘国庆,徐诚

（南京理工大学机械工程学院,江苏南京 210094）

狙击步枪弹挤进过程对狙击步枪射击精度的影响很大,而坡膛的结构参数又是影响挤进过程的一个重要因素。为了揭示坡膛对挤进过程的影响,通过一套设计的试验装置,进行了两种不同坡膛工况下狙击步枪弹的准静态挤进试验,得到坡膛锥角对挤进力的影响情况；采用非线性有限元方法模拟挤进过程,建立弹头挤进过程有限元计算模型,分析仿真结果得到了多组坡膛锥角与挤进力间的关系及其挤进力的组成与各部分所占比重,发现狙击步枪弹不同于其他弹头的挤进特性,同时揭示了狙击步枪弹挤进力的形成机理；依照坡膛、狙击步枪弹的结构特点将挤进过程分为5个阶段,推导出各阶段上挤进力函数表达式；从试验、仿真与理论3个方面研究狙击步枪弹准静态挤进特性,对了解狙击步枪弹挤进过程与弹/枪参数匹配机理具有重要意义。

兵器科学与技术；弹头挤进；坡膛锥角；挤进试验；有限元；弹/枪相互作用

0 引言

狙击步枪的弹头挤进过程对整个膛内时期的火药燃烧有着较大影响,挤进条件的改变又影响着最大膛压及其弹头初速,进而影响射击精度。挤进过程受多个因素影响,如坡膛锥角、阴阳线宽度比、弹头过盈量等,深入研究各个因素对挤进过程的影响,有利于寻求弹/枪间的参数最佳匹配关系,对揭示弹/枪间的相互作用具有重要意义,

挤进过程是一个非常复杂的非线性力学过程,也是一个大变形、带过盈配合的接触问题[1],弹头在火药力的作用下逐步嵌入线膛,随之发生弹性变形、塑性变形。文献[2]以某型火炮为研究对象,将数值仿真分析结果与内弹道方程耦合,给出了两种坡膛工况对火炮内弹道及其挤进力的影响情况。文献[3]认为火炮弹丸在整个挤进过程中,身管内膛是直接作用于弹丸的外部约束,弹丸刻痕与内膛参数密切相关。文献[4]考虑了高速挤进过程中应变率对弹丸材料的影响,建立了一种使用2阶系统模拟弹丸挤进力的计算方法,得出动态挤进过程挤进力随膛压的变化关系。文献[5]研究了埋头炮弹带挤进过程中流变应力、摩擦系数,提出流变应力可通过两种方法估算,即动态系数修正法与图解法。文献[6]比较了3种不同坡膛锥角对启动压力的影响,指出当锥角一定时,弹丸的启动比冲量消耗基本不变。

上述研究主要是针对火炮弹丸进行的,迄今为止关于狙击步枪弹挤进过程的研究较少。狙击步枪弹是前收口二件套结构,弹头壳与铅芯共同参加挤进过程,挤进机理不同于炮弹的挤进,无法将上述研究成果应用于狙击步枪弹的挤进过程。本文以某高精度狙击步枪为研究对象,从试验、理论和仿真3个方面研究狙击步枪弹挤进过程,探寻弹头挤进机理,了解坡膛结构参数对挤进过程的影响,为狙击步枪系统设计提供理论依据。

1 准静态挤进试验

1.1 试验条件

取某高精度狙击步枪身管两根并将其截短如图1所示,截短后弹头在身管内行程为60 mm左右,记录该挤进行程上的挤进力足够反映出坡膛对挤进的影响情况,两根身管的坡膛锥角分别为1°15′和1°45′.设计了一套用于挤进的试验装置,其装配图如图2所示,其中推杆、定心轴套与身管的同轴度需要重点保证。CMT5105材料试验机提供挤进动力,并由其内置的力传感器检测挤进力,最后由专用PC机处理后记录挤进力。压头推进速度为15 mm/min.试验装置实物图如图3所示。

图1 截短后的身管Fig.1 Shortened barrel

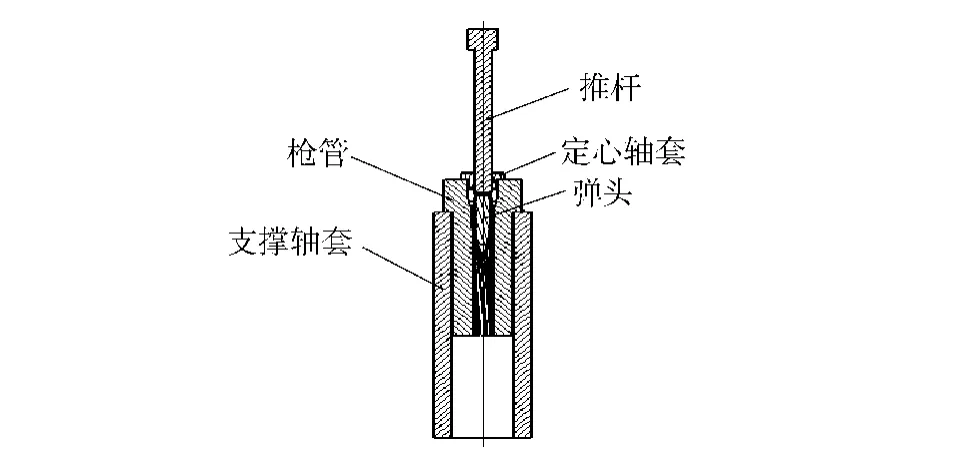
图2 挤进装置装配图Fig.2 Assembly drawing of engraving device

图3 挤进试验装置实物图Fig.3 Engraving experimental setup

1.2 试验结果及讨论

1.2.1 狙击步枪弹弹头变形

准静态挤进试验前后弹头的变化如图4所示。挤进时材料试验机压头下压推杆,推杆推动弹头沿身管内膛轴线运动,弹头受到坡膛与膛线的挤压而发生变形,随着挤进的深入,弹头材料逐渐由弹性变形过渡为塑性变形,塑性变形形状受膛线影响,当挤进完成时弹头外圆部形成图4（b）所示刻痕。

图4 弹头挤进前后对比Fig.4 The change of bullet before and after engraving

挤进时,具有过盈量的外圆部在膛线的挤压下产生形变并形成刻痕,形变量与刻痕尺寸由内膛结构决定。挤进完成后弹头外圆部最大直径等于阴线直径7.81 mm,弹头刻痕深度为狙击步枪阴阳线半径差值0.095 mm,刻痕的宽度等于阳线的宽度值1.036 mm,同时由于膛线缠角的影响,刻痕与弹头轴向成4.49°夹角。

1.2.2 挤进力变化趋势分析

截短后的身管除坡膛锥角外,其他结构尺寸及状态均相同,两种坡膛工况实测挤进力数值如图5所示。由图5可知挤进力数值变化较为平缓,整个过程没有出现突变数值点或异常变化趋势。坡膛锥角为1°45′的身管挤进试验所测最大挤进力为2 237.5 N,挤进完成后挤进力保持平稳,约为2 000 N左右,锥角为1°15′的身管试验所测最大挤进力为2 925.9 N,挤进完成后挤进力保持在2 600 N左右,最大挤进力与平稳阶段的挤进力比1°45′的身管所测增大了约30%.

图5 试验实测挤进力数值Fig.5 Experimental data of engraving force

从试验实测挤进力变化趋势可知,弹头从开始挤进到最终挤出身管过程可分为3个阶段：第1阶段为挤进力线性增长阶段,推杆推动弹头匀速沿身管轴线运动,弹头外圆部在坡膛、膛线挤压下产生弹塑性变形,挤进力随挤进深度加深而增加,直至达到最大值。此阶段挤进力迅速增加并基本呈线性规律变化,小的坡膛锥角其线性增长速度快。第2阶段为挤进力平稳保持阶段,挤进力在达到最大值之后进入下降阶段,最终下降至沿轴向运动的摩擦阻力值,此后基本保持不变。轴向摩擦力主要由阴阳线圆周面上的摩擦力与导转面上的摩擦力组成。此阶段弹头完成最终塑性变形,外圆部形成与膛线相吻合的刻痕。第3阶段为挤出阶段,是准静态挤进试验的最后结果,但对试验内容无实际意义。

2 有限元计算分析

2.1 有限元模型与材料参数

依据身管内膛尺寸与弹头外形参数建立三维模型,使用有限元前处理软件划分网格,以6面体缩减积分单元（C3D8R）为主对身管和弹头进行有限元网格划分。身管坡膛对挤进过程影响较大,故对其进行网格加密处理,在轴向长度上共划分10个单元,其轴向密度为整体轴向密度的3倍。膛线深度尺寸远远小于身管外圆径向尺寸,为保证计算精度同时降低计算成本,将阳线与身管外圆分离单独划分网格,有助于精确获得挤进过程中二者间的相互作用关系。

狙击步枪弹弹头壳包裹铅芯,弹头壳为主要承受挤压部分,故在厚度方向上划分4层网格,受挤压的外圆部在轴向上进行网格加密,加密后的单元网格尺寸为0.1 mm×0.1 mm×0.15 mm,共划分205 769个网格。铅芯在挤进过程中同样产生变形,但其材质较软且流动性强,因此对挤进过程的影响较小,故其网格划分较为稀疏,共划分110 868个网格。网格划分完毕后弹头与身管的有限元半剖装配图如图6所示。

图6 有限元装配半剖图Fig.6 The finite element half sectional assembly drawing

身管材料为高强度钢,弹头壳材料为黄铜,弹头芯部为铅,弹头材料采用双线性材料模型。相关材料基本力学性能参数如表1.

表1 力学性能参数表Tab.1 Parameters of mechanical properties

2.2 接触与边界条件的设置

采用面-面接触类型定义弹头壳外表面与身管内膛之间、弹头壳内表面与铅芯表面之间的接触,接触从初始步即开始作用。接触控制算法采用惩罚函数法,其主要原理为当从面节点穿透主面时,求解器在节点上施加一个反作用力来将其拉回到主面之上,阻力的大小与穿透量呈正比关系,从而能够有效避免从面节点对主面的穿透。

边界条件施加的目的是保证计算模型的约束状态与实际一致。准静态挤进试验中身管被支撑轴套约束轴向位移,弹头被推杆沿轴向推动,在有限元模型中以约束身管凸台下表面节点轴向自由度与在弹头后表面节点施加位移约束来模拟推杆和支撑轴套的作用。

2.3 求解器的选择

准静态挤进过程中,弹头外圆柱部被膛线挤压形成刻痕同时伴随着材料的塑性流动,本质上是一个具有大变形的复杂接触问题。ABAQUS/Standar求解器适于模拟静态、准静态的各种非线性问题,但在处理复杂的接触问题时难以收敛,从而导致大量的迭代甚至计算失败,故使用ABAQUS/Explicit求解器来模拟整个挤进过程,该求解器应用显式积分求解技术分析复杂的接触问题,具有效率高、速度快、占用磁盘和内存小等特点。

2.4 结果与分析

2.4.1 模型的试验验证

对有限元模型进行求解,获得两种坡膛锥角工况下挤进力数值仿真结果与试验实测值对比情况如图7所示。

从图7中可以看出,数值仿真所得挤进力结果在线性增长阶段、下降-平稳阶段和挤出阶段较好地符合了试验实测情况,如坡膛锥度1°15′模型,数值仿真值各个阶段与试验值最大误差依次为7.8%、10.7%、8.1%,且两种方法所得挤进力的变化趋势也基本一致,证明了本文建立的挤进过程有限元计算模型的正确性和有效性。

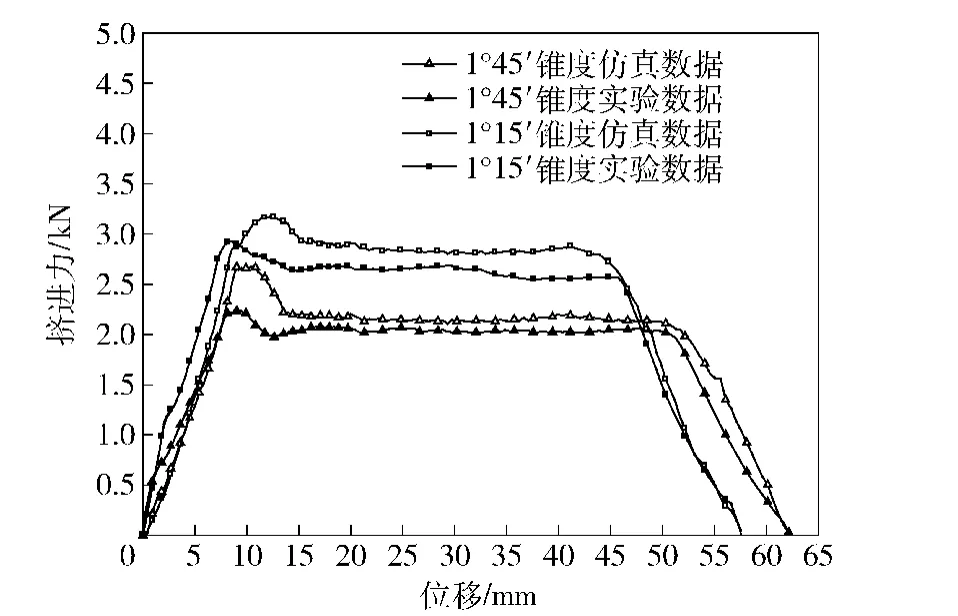
图7 挤进力数值仿真结果Fig.7 The numerical simulation results of engraving force

2.4.2 挤进力组成分析

挤进力包括轴向摩擦力和克服弹带材料变形而产生的力,试验实测挤进力数据无法反映出这两个部分力的大小及其变化趋势,但数值计算却能较容易得到上述结果,挤进力分解结果如图8所示。

图8 轴向摩擦力、克服材料变形阻力与位移关系Fig.8 The relation among displacement,axial friction and deformation resistance

由图8可以看出,轴向摩擦力是挤进力的主导部分,轴向摩擦力的大小与接触面积、接触面上的正压力有关,较小的坡膛锥角使得坡膛轴向长度增加,故在挤进时弹头与坡膛接触面积增大,这也是1°15′锥角坡膛挤进力比1°45′锥角坡膛大的原因之一。克服材料变形阻力在完成挤进后基本消失,且两种坡膛工况下克服材料变形阻力在变化趋势以及数值上基本相同。完成挤进后挤进力约等于轴向摩擦力。

值得说明的是,弹头挤进过程中克服材料变形阻力、挤进力与轴向摩擦力并不是同一时刻达到最大值,对应时刻弹头轴向位移数据如表2所示。

表2 材料变形阻力、挤进力、轴向摩擦力最大时弹头位移Tab.2 The displacement of bullet when the deformation resistance,engraving force and axial friction are maximal

分析计算模型发现,当弹头最大外圆圆周线与坡膛接触时克服材料变形阻力达到最大值,当挤进完成时轴向摩擦力达到最大值,挤进力在这两个位置之间的某个时刻达到最大值,这是不同于具有弹带结构的弹头挤进时的特性。发生这种现象的主要原因为狙击步枪弹头是通过外圆部的过盈替代弹带导转弹头在膛内的运动,狭长的锥形结构使得轴向长度大于坡膛的长度,当弹头前部外径较小的部分已完成塑性变形时,后部尚未接触坡膛或未完成挤进所需塑性变形,故而出现3种力依次达到最大值的现象。

2.4.3 坡膛锥角变化对挤进力的影响

准静态挤进试验获得了两种坡膛锥角工况下挤进力的变化,为进一步研究坡膛锥角与挤进力间的关系。本文增加了2°和2°30′锥角坡膛工况下的计算实例,4种不同坡膛锥角下的计算结果如图9所示。

图9 各锥角坡膛挤进力对比Fig.9 The comparison of engraving forces with different angles

由图9可知,锥角增加导致了挤进力的减小。通过分析挤进力的组成可知克服材料变形力各锥角坡膛均相差无几,在摩擦系数一定的情况下,挤进力正比于弹头接触内膛所受正压力。考查身管与弹头的接触应力能较直观反映坡膛锥角对挤进力的影响原因,取弹头刻痕处上某一单元与身管阳线起始处某一单元,绘制不同坡膛锥角工况下的应力历程曲线,如图10所示。

图10 弹丸、阳线某处应力历程曲线Fig.10 The Mises course curves of points on score and riffling lands

由图10（a）可知,较大的坡膛锥角使得其轴向长度减小,导致刻痕处的应力上升较快,但是由于挤进时弹头变形急促且充分,故挤进后刻痕处的应力较小,进而影响挤进力的大小。图10（b）给出了身管阳线起始处应力变化情况,图中最大应力值随锥角的增大而增大,其原因主要是短的坡膛挤压弹头形成刻痕时较为迅速,使得阳线起始处所受力也会相应提升,这在坡膛结构设计时应当被重视。

3 挤进力理论计算公式

本节重点建立弹头挤进力理论计算公式。公式计算方便、易于通过程序编制计算语言,能够直接应用于狙击步枪设计中。

3.1 假设条件

狙击步枪弹弹头导引外圆部轴向长度大于身管坡膛轴向长度,故弹头挤进过程中弹头壳表面会依次或同时与坡膛、阴阳线及导转侧相接触,随着挤进的深入,接触面积逐渐增大并形成刻痕,接触过程中弹头材料必然处于屈服或流动状态[7]。从理论上计算弹头挤进力与位移间的关系,作以下假设：

1）弹头材料与坡膛之间应力保持不变,发生接触变形时材料即达到其屈服极限值σ.

2）挤进力的变化是由接触面积引起的,即Fn= σA,其中A为接触面积。

3）接触只发生在坡膛、阴阳线圆周线、导转侧面上,弹头材料受挤压变形,无材料流动及切屑现象。

4）不考虑弹头材料的形变硬化。

3.2 计算公式及算例

参照文献[7]中计算火炮挤进力的方法,推导弹头准静态挤进力计算公式,主要考虑结构特点对挤进力的影响。弹头弧形部尺寸复杂,故对其结构做适当简化,不考虑身管及其弹头结构尺寸的加工误差,二者初始接触时的结构示意图如图11所示,其中dl为阳线直径,dg为阴线直径,dc为弹头与坡膛初始接触处的外圆直径,dmax为弹头最大外圆直径,S、L1、L2、L3、L4、L5分别为结构尺寸,φ为坡膛锥角,θ膛线缠角,α为弹头弧形部前倾角,μ为静摩擦系数,n为膛线数目,a为阳线宽度,b阴线宽度,σ为弹头材料的屈服极限。

图11 挤进结构示意图Fig.11 Schematic diagram of engraving structure

根据以上假设及结构特点,将挤进位移分为5段,每段的具体含义如下：

第1段：A点到O点。

第2段：在第1段基础上,由B点到P点。

第3段：在第2段基础上,由C点到Q点。

第4段：在第3段基础上,由D点到P点。

第5段：在第4段基础上,由E点到O点。

分段是以接触面积的变化形式为依据的,同一段内的接触面积与弹头位移量x的函数关系式相同,不同段位移上的接触形式不同,如弹带与坡膛在不同阶段的接触面积可处于不断增大或不断缩小的状态,故挤进力-位移曲线的函数形式亦不同。挤进力计算公式基于塑性变形与力学原理。根据以上假设,当发生接触变形时即认为弹头与身管间产生了正压力,同时由于锥角和摩擦的存在导致弹头受到轴向的挤进力,阻力的变化与弹头位移有关。以x代表弹头位移量,每段上的挤进力计算公式如下：

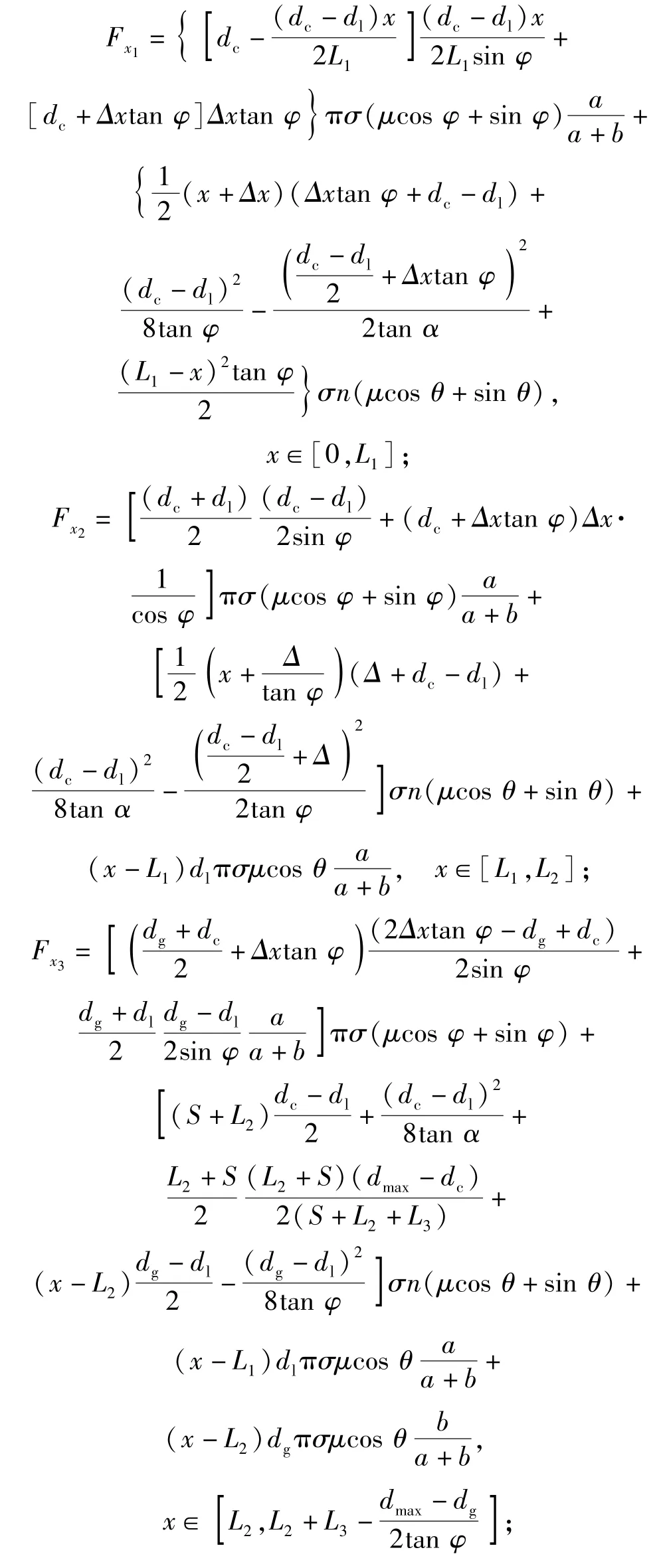
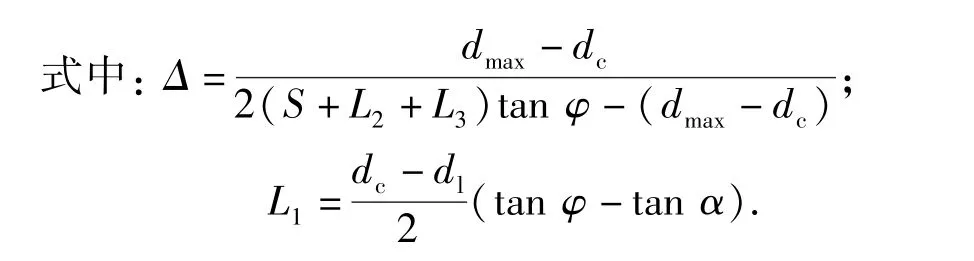
在挤进力分段函数中,坡膛锥角、弹头前倾角、静摩擦系数μ与材料屈服极限σ影响挤进力的函数表达形式。使用上述分段函数计算坡膛锥角为1°45′所得曲线与试验实测曲线对比如图12所示。

图12 计算曲线与试验曲线对比Fig.12 The comparison of calculated and test curves

图12所示计算曲线是分段连续的,描述了从开始挤进到最终完成挤进过程中挤进力与弹头位移间的关系,挤进完成时曲线变为一条水平线即挤进力保持不变。计算所得曲线与试验实测曲线变化趋势基本一致,证明准静态挤进力计算公式的有效性,可作为预估准静态挤进力的一种方法,但计算曲线仍与试验实测曲线有一定差距,如挤进第一阶段完成时挤进力试验值约为700 N,而计算值仅为450 N左右,误差主要来自于计算忽略了弹头弧形部,材料屈服极限、摩擦系数的偏差也是导致误差的因素,从而导致计算值偏小。计算公式受结构尺寸、材料力学性能、摩擦系数等因素影响,故上述公式仅适用于7.62 mm狙击步枪弹挤进力的计算。

4 结论

本文以高精度狙击步枪为研究对象,进行了狙击步枪弹弹头准静态挤进试验,建立了挤进数值仿真模型,同时推导了挤进力的理论计算公式,分析所得结果形成主要结论如下：

1）坡膛锥角大则挤进力小,主要原因是坡膛锥角大则坡膛轴向距离短,挤进时弹与膛的接触面积较小,另一方面大的坡膛锥角使完成挤进后刻痕上的过盈应力值较小,从而使得挤进力减少。

2）挤进力可分为克服材料变形阻力与轴向摩擦力两部分。克服材料变形阻力基本不受坡膛锥角影响,是挤进力较小的组成部分。轴向摩擦力与接触面积、接触面上的应力值呈正比,是挤进力主要组成部分。

3）弹头克服材料变形阻力、挤进力与轴向摩擦力并不是同一时刻达到最大值,而是在时序上依次达到最大值。挤进力达到最大值的时刻不是弹头完成挤进时刻,这是与具有弹带结构弹丸挤进过程的区别。不同锥角的坡膛达到最大挤进力的位置亦不同。

4）本文建立的弹头挤进过程数值仿真模型经试验验证是正确、有效的,能够作为一种计算狙击步枪弹弹头挤进力的方法,有助于进一步开展对弹/枪参数最佳匹配关系的研究。

5）根据坡膛与弹头的结构特点,推导了挤进力的理论计算公式；计算公式基于塑性变形与力学原理,构造挤进力与接触面积间的关系式,而接触面积是弹头位移量的分段函数。通过算例与试验曲线的对比验证了公式的正确性。

（References）

[1] 何勇.弹丸挤进阻力的一维模型及计算[J].弹道学报,1994, 6（4）：24-28.

HE Yong.The one-dimensional model and calculation of projectile's engraving resistance[J].Journal of Ballistics,1994,6（4）： 24-28.（in Chinese）

[2] 孙河洋,马吉胜,李伟,等.坡膛结构变化对火炮内弹道性能影响的研究[J].兵工学报,2012,33（6）：669-675.

SUN He-yang,MA Ji-sheng,LI Wei,et al.Study on influence of bore structure on gun's interior ballistic performances[J].Acta Armamentarii,2012,33（6）：669-675.（in Chinese）

[3] 樊黎霞,何湘玥.弹丸挤进过程的有限元模拟与分析[J].兵工学报,2011,32（8）：963-969.

FAN Li-xia,HE Xiang-yue.Finite element simulation and process analysis of projectile entering into barrel[J].Acta Armamentarii, 2011,32（8）：963-969.（in Chinese）

[4] 金志明,曾思敏.弹丸挤进过程的计算与研究[J].兵工学报, 1991,12（1）：7-13.

JIN Zhi-ming,ZENG Si-min.A study on the calculation of the engraving process on projectiles[J].Acta Armamentarii,1991, 12（1）：7-13.（in Chinese）

[5] 张浩,周彦煌.埋头弹火炮挤进过程研究[J].弹道学报,2006, 18（1）：76-79.

ZHANG Hao,ZHOU Yan-huang.Research on the engraving process of CTA[J].Journal of Ballistics,2006,18（1）：76-79. （in Chinese）

[6] 米粮川,高树滋,赖长缨.内弹道弹带挤进过程仿真研究[J].弹箭与制导学报,2012,32（1）：133-135.

MI Liang-chuan,GAO Shu-zi,LAI Chang-ying.The simulation study on band edging properties in interior ballistics[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32（1）：133-135.（in Chinese）

[7] 周彦煌,王升晨.两相流内弹道学[M].北京：兵器工业出版社,1990.

ZHOU Yan-huang,WANG Sheng-chen.The study of two-phase flow property of interior ballistics[M].Beijing：Publishing House of Ordnance Industry,1990.（in Chinese）

Research on Quasi-static Engraving Force of Sniper Rifle Bullet

LIU Guo-qing,XU Cheng
（School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China）

The engraving process of sniper rifle bullet has a great influence on the firing accuracy of sniper rifle,which is closely related to the bullet ramp.In order to reveal the effect of bullet ramp on engraving process,a test device is designed for the quasi-static engraving experiments under two different conditions of bullet ramp,and the influence of forcing cone angle on engraving force is obtained.A finite element model is established to simulate the engraving process based on the theory of nonlinear finite element.The simulation results reveal the relationship of forcing cone angle and engraving force,the composition of engraving force,the proportion of each part and the formation mechanism of engraving force,and show that the engraving characteristics of sniper rifle bullet are different from those of other bullets.Furthermore,the engraving process is divided into five parts according to the structures of bullet and bullet ramp,and the formula of each part is derived.The quasi-static engraving process of sniper rifle bullet is studied in three aspects：experiment,simulation and theory,which is helpful in understanding the engraving process of sniper rifle bullet,and the matching mechanism of bullet and bullet ramp.

ordnance science and technology；bullet engraving；forcing cone angle；engraving experiment；finite element；interaction of bullet and sniper rifle

E932.1

A

1000-1093（2014）10-1528-08

10.3969/j.issn.1000-1093.2014.10.002

2013-12-27

国防基础科研项目（A2620061288）

刘国庆（1988—）,男,博士研究生。E-mail：guoqingcool@126.com；徐诚（1962—）,男,教授,博士生导师。E-mail：xucheng62@mail.njust.edu.cn