基于AHP与广义最短距离的GIS选址方法

易鸿杰 ，李平

(宜昌市测绘大队，湖北 宜昌 443001)

1 引 言

GIS 强大的数据管理功能、查询分析功能和数据显示功能，使得其应用于空间选址时避免了纯数学方法繁琐的数学计算，较易考虑多种因素的综合影响，选址结果也更直观。现阶段利用GIS 进行空间选址多基于层次分析法的多准则决策分析模型，所得到结果为适宜性最高的一片区域。而出于经济效益和社会成本考虑，很多设施，特别是公共服务设施在选址时要求到周围服务点距离之和尽量的小。本文提出基于层次分析法(AHP)和广义最小距离的GIS 选址方法，所得结果为层次分析法求得选址结果中到附近服务点距离之和为最小的点，并以某一区域内公共停车场选址为例，验证其科学性。

2 基于AHP 与广义最短距离的GIS 选址方法

2.1 层次分析法

层次分析是由美国运筹学家提出的一种将定性与定量结合起来，通过多种影响因素的两两对比来为决策分析提供定量依据的方法。该方法的主要思想是根据需解决问题的总目标，将该问题的影响因素列举出来，然后按照这些影响因素之间的相互影响和隶属关系关系将这些因素聚集组合成不同的层次，从而得到多层次的分析结构模型。根据这个结构模型，问题可以归结为确定最底层相对于最高层的相对重要权值。

其应用于空间选址的一般步骤为:

(1)选择评价指标，即确定影响因素;

(2)建立层次结构模型。层次结构模型分三层，最上层为目标层，为问题的总目标;中间为准则层或指标层，为实现目标所涉及的中间环节各因素，最下层通常为方案或对象层P，在影响因素超过9 个时可将准则层分为若干子层;

(3)构造判断矩阵，矩阵中元素aij为因素Bi相对于因素Bj对目标的影响程度，其值大小根据成对比较法和1－9 比较尺度确定，假设aij=1，则表示i 元素相对于j 同等重要，aij=9，表示i 元素相对于j 极端重要，

(4)计算各影响因素的相对权重，并进行一致性检验;

(5)利用缓冲分析和叠加分析等方法在GIS 中得到每种影响因素的适宜性分级图;

(6)对这些适宜性分级图进行加权叠加分析，并重分类进行渲染得到结果。

2.2 基于广义最短距离的GIS 选址方法

距离模型是选址方法中最简单和最能直观反映其可达性的模型，传统距离最小模型和基于GIS 的广义最短距离模型分别为:

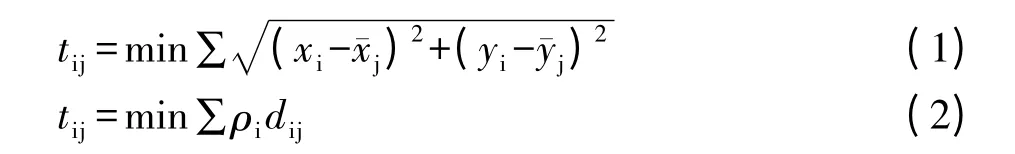
式(1)中:tij为选址结果到所有吸引源的直线距离之和;(xi，yi)为吸引源的坐标;为规划选址的坐标;

式(2)中:tij为选址结果到所有吸引源的广义最短距离;ρi为吸引源的权重;dij为考虑到路网的候选地址点到吸引源之间的距离。

由以上两式可看出，传统距离最小模型将两点间路径视为直线，且未考虑服务点的相对重要性，偏离实际。

基于AHP 和广义最小路径的GIS 选址方法的思想是:在利用层次分析法求得适宜性高的区域中，求取一个点，使其通过路网结构到达吸引源的最短距离之和为最小。

相关算法:

(1)圆与多边形求交算法:用区域分割法可求得多边形与多边形的焦点，圆与多边形求交点是多边形与多边形求交点的特殊情况。区域分割法求任意多边形A 与任意多边形B 交点的算法思想是从多边形所在的平面几何区域考虑，通过区域分割将几何平面分割为若干个小区域，然后在每个小区域内求两个多边形所在小区域部分的交点。算法的基本思路是:

①求得两多边形的包围盒矩形的公共部分;

②对步骤1 中求得的公共部分进行矩形格网划分，得到若干个面积相等，形状相同的单位矩形网格;

③求得两个多边形在几何位置上在各个网格内对应的边的集合;

④针对每一个网格求两个多边形对应的边的交点。给定一个网格，用EA表示多边形A 在该网格内对应的边的集合记，用EB表示多边形B 在该网格内对应的边的集合，求得EA与EB中各个元素的交点;

求得每一个网格中的所有交点后，这些交点的集合即为所得结果。

(2)Dijkstra 算法

迪杰斯特拉(Dijkstra)算法是一种较为典型的单源最短路径算法。该算法在GIS 中能轻松实现。它具有以起始点为中心向外层层扩散一直到终点的特点，通过该算法可以计算出从一个确定节点(源点)出发，通往其他所有节点的最短路径。

该算法的基本思想是:对于一个确定的带权有向图G={V，E}，式中V 为节点集合，V 为有向弧的集合，将V 分为S 和U 两组，S 表示已经求出最短路径的节点的集合，U 为剩余的节点集合，S 初始情况下只有源点这一个元素。在每求得一条最短路径之后，就将所对应的到达的节点由U 中移到S 中。在将U 中的元素移到S 直到U 为空的过程中，必须确保源点到S 中各元素的最短路径值不大于源点到U 中任意一节点的最短路径值。

该算法的执行步骤是:

(1)初始化S，使其含有元素只有源点α，S={α};

(2)从U 中搜索到源点α 距离为最小的顶点k，把k 由U 移至S 中，此时这个值为最小的距离即为源点α 到k 的最短路径长度;

(3)考虑是否经过k 点，修改源点α 到U 中各元素的距离;若从源点α 经过k 点到U 中一节点u 的距离小于原来的距离(不经过顶点k)，则修改源点k 节点u 的距离值，修改后的距离值为α 到节点k 的距离与节点k 到u 边上的距离乘以权值之后的和;

(4)重复第(2)步和第(3)步，直到U 为空。

2.3 基于AHP 和广义最短距离的GIS 选址方法的实现

首先利用基于层次分析法的GIS 选址模型求得备选地址集，为若干个多边形，为了减少运算量，将这些多边形进行格网划分并提取格网中心坐标，然后在这些格网中心点中寻找到附近服务点距离之和D 为最小的点。

求取任意格网中心点D 值的方法为:

将所有服务点的位置V 和道路交叉点的位置K视为网络的节点V=(υ1，υ2，…υn，kn+1，kn+2，…km)，并重要性给赋予服务点权值P=(ρ1，ρ2，…ρn)，连接这些它们的道路视为网络的弧E=(e1，e2，…em)，此时即有一个有向连续网络G={V，E}。以任意格网中心点α为圆心，以γ 为半径作圆，γ 从0 开始等间距递增，根据该设施的服务半径对γ 设上限，在圆与路网有交点时记该交点为li，并将点α 和li视为有向权图G 中新的顶点，连接这两点的直线视为新的弧，则可利用Dijkstra 算法求得li到所有vi点的最短距离d(li，vi)，进而可求得由点α 出发，经由li到vi点的最短距离d(li，vi)+γ，即可求得经过li到所有服务点的最短距离之和，所有交点li中的最小值即为D。

3 实例分析

本文通过ArcGIS 软件，以某一城区公共停车场选址为例，验证本方法科学性和可行性。

3.1 层次分析法选址

首先确定选址影响因素，并搜集相关的数据。将所有空间数据转化为同一坐标系导入ArcGIS 中，并将非空间数据与空间数据对应起来录入属性表中。停车场必须与医院和学校保持一定的距离，其与主干道的距离反映了可达性，同时结合这一区域的实际情况，考虑与客运站和城市出入口的距离以缓解城市对外交通所带来的压力，人口密度可反映出区域的泊车量，以土地利用性质反映拆迁费用。本文选取了以下5 种影响因素:与医院和学校的距离S1、与客运站和城市出入口的距离S2、与主干道的距离S3、人口密度S4、土地利用性质S5。

根据专家打分，构造的判断矩阵为表1:

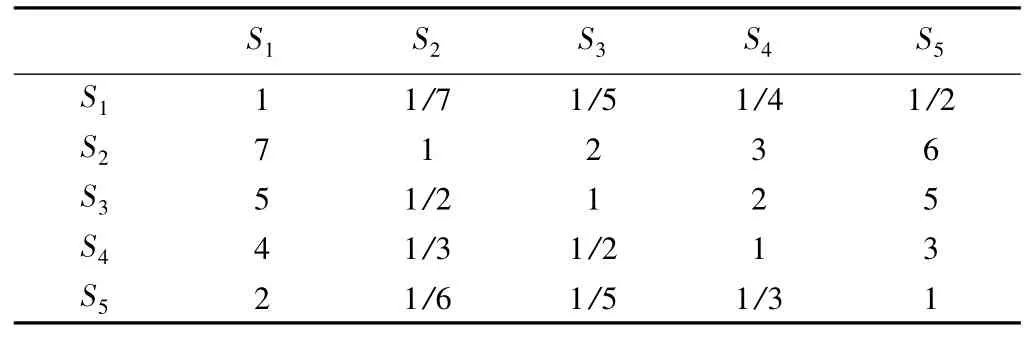
表1 判断矩阵的构建

用和集法计算出判断矩阵最大特征值为λmax=5.085，特征向量为(0.085582106，0.796618894，0.502046106，0.301044077，0.124081469)，

对其进行一致性检验:

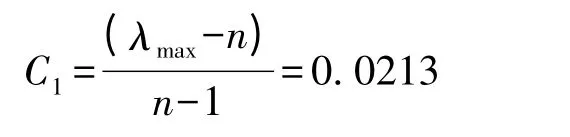
C1小于0.1，该矩阵具有满意一致性。此时将特征向量归一化为 (0.04729932，0.44027353，0.27746971，0.166380362，0.068577067)。

在GIS 中对各影响因素进行重分类。分类的分级值、评分值及对应的权重如表2所示:

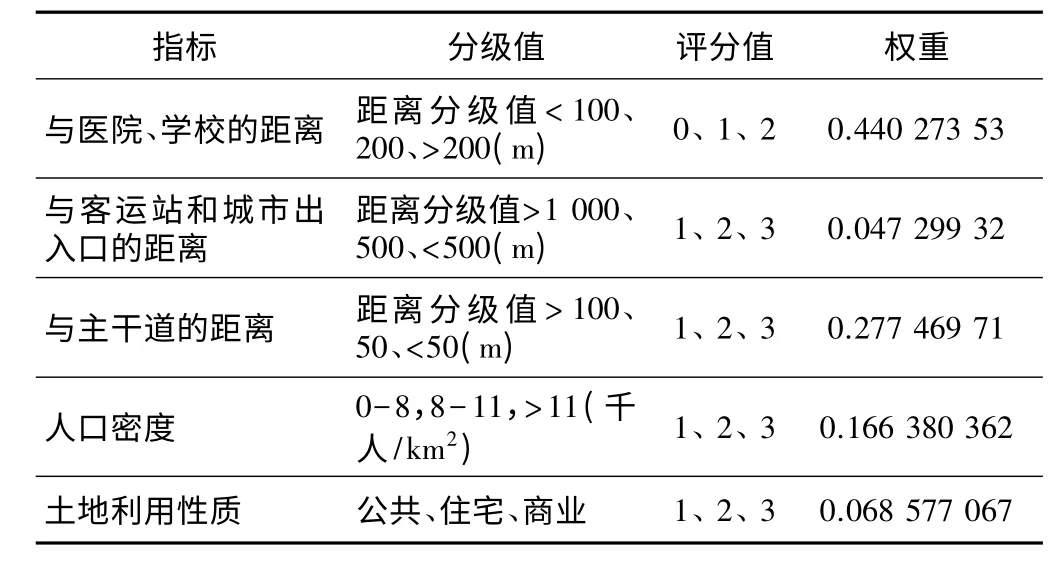
表2 影响因素的分级值、评分值及权重

在GIS 软件中利用缓冲分析、叠加分析等空间分析方法分别得出以上5 种因素的适宜性分级图。图1、图2分别为考虑S1 和S2 两因素的适宜性分级图:

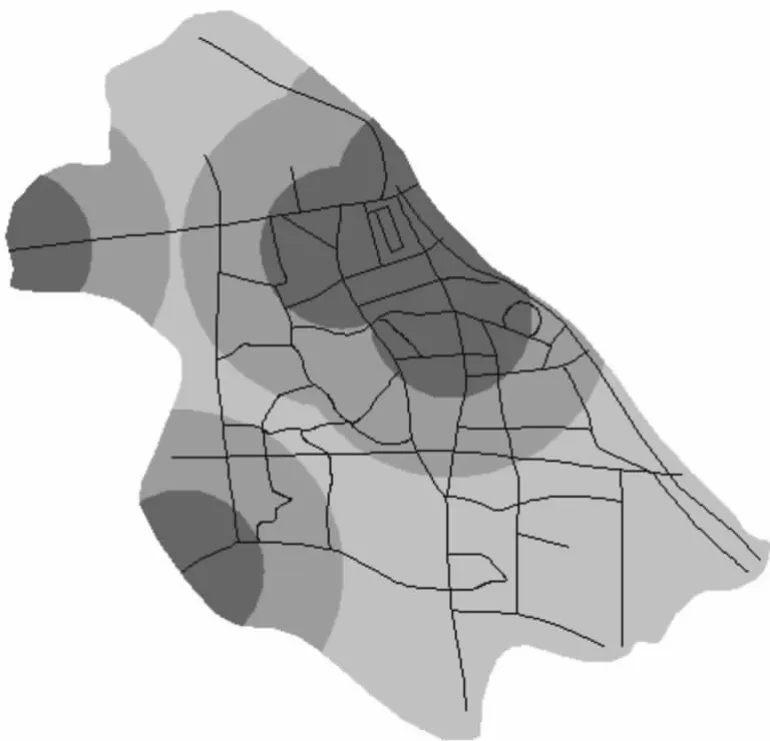
图1 城市出入口与客运中心的影响

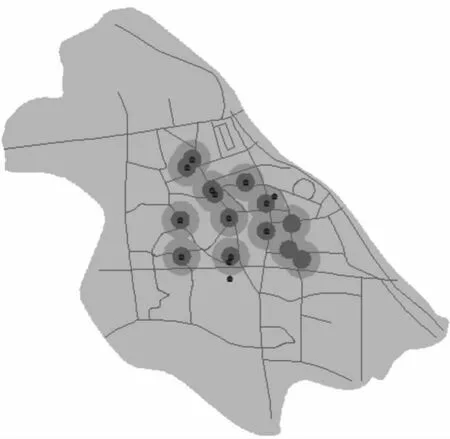
图2 医院学校的影响

根据表2中各因素的相对权值，对5 种影响因素的适宜性分级图进行栅格叠加运算，并进行渲染后，得到考虑以上5 种因素的选址最适宜区域，栅格叠加过程和求得选址结果如图3、图4所示:

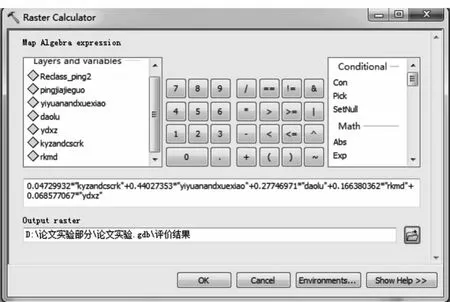
图3 ArcGIS 栅格叠加器

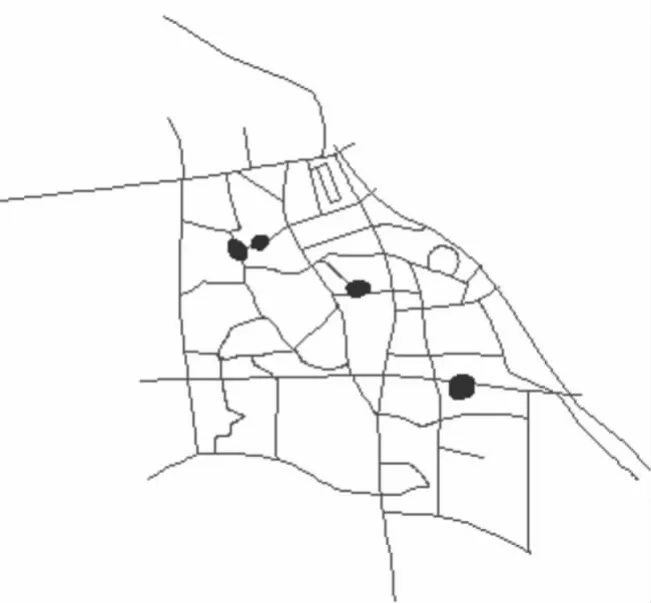
图4 层次分析法求得选址区域

3.2 基于广义最短距离的GIS 选址

层次分析法所得为整个城区的适宜性高的区域，考虑到公共停车场的服务半径，可根据一定的规则将城区划分为若干小区域，对每一小区域进行单目标选址。

现以图4中居中的多边形所在小区为例，寻求该多边形中基于广义最短路径的最佳选址点。以该区域内商场、购物中心、游乐场等停车吸引源吸引的日均停车量作为的权值。该多边形经过再次栅格化后由17个实际边长为15 m的格网单元组成，求得这17 个栅格中心点到小区内所有停车吸引源的广义最短距离，给栅格单元添加新的属性值P=1/D，并根据P 值的大小对图形进行渲染。由此距离的影响即可通过栅格单元颜色的深浅反映出来。

4 结 论

相较于传统的数学选址方法，利用GIS 进行空间选址由于其强大的空间分析功能和友好的人机界面具有无可比拟的优势。基于层次分析模型的GIS 空间选址方法能灵活、快速对数据进行分析处理，综合考虑多重影响因素，基于广义最短路径的GIS 选址模型比传统的距离模型更符合实际，能得到从距离角度考虑的最佳位置。两者结合起来的方法综合了两者的优势，使结果更精确。

［1］刘小林，温程杰，张江水．运用GIS 进行空间选址分析［J］．测绘与空间地理信息，2010，(33)4:19～21．

［2］刘李霞，毕华兴，孙宪娟等．基于改进层次分析法的GIS公共服务设施选址［J］．地理与地理信息科学，2011，27(5):46～50．

［3］陈建飞．地理信息系统导论［M］．科学出版社，2003．

［4］姚辉学，卢章平．一种任意复杂程度二维多边形的求交算法［J］．工程图学学报，2006，2:127～131．

［5］韩世莲，李旭宏，刘新旺等．多人多准则模糊层次分析法的物流中心综合评价优选模型［J］．系统工程理论与实践，2004(7):128～132．

［6］唐少军．基于GIS 的公共服务设施空间布局选址研究［D］．长沙:中南大学，2008．