SSSC对提高多机电力系统频率稳定性的控制研究

/三峡大学电气与新能源学院 李飞 中国电力建设集团中南勘测设计研究院有限公司 俞凯/

0 引言

随着洁净的可再生能源的并网越来越受到重视。导致系统的运行控制方式向多样化转变，这些因素对现代互联电力系统的稳定运行提出了更高的要求[1]。传统的控制频率稳定的措施通过在发电机侧安装电力系统稳定器（PSS）可以很好地抑制本区域内的波动，而无法满足互联系统区域间对于频率稳定性的要求[2]。

近来年通过充分挖掘FACTS的利用价值，找到了其对系统提供的附加阻尼的一个潜在益处。

SSSC作为新一代串联型 FACTS控制器，其原理是通过向线路中注入一个可控电压源，无需装设任何电容或电抗器就可以达到有效的控制电网潮流和稳定[3]的目的，从而避免采用其他单方向减少线路阻抗能力的装置（如TCSC）引起的谐振问题。

本文分析了SSSC为系统提供的阻尼作用的机理，为了有效地抑制系统频率大幅波动，文中讨论了SSSC的控制规律，并利用相位补偿法[4]整定控制器参数。仿真算例采用水轮机-汽轮机联合发电系统模拟多机电力系统的运行情况，在有功功率扰动下（如机组出力与负荷的波动等），分析在安装SSSC前后，各机组的频率变化及联络线功率的变化特征。算例的结果表明装设SSSC能有效抑制系统的频率大幅波动，提高系统的稳定性。

1 SSSC对系统的阻尼作用分析

在分析SSSC对系统的阻尼作用是，首先需要建立电力系统的动态模型，在此需引入电力系统 Phillips-Heffron 模型[5]，得到在某一稳定运行点（即平衡点）处的线性化模型，也即全系统传递函数框图，利用控制理论方法分析安装SSSC装置后对系统转矩的贡献，用来分析SSSC的投入对于提高系统稳定性的机理。

以单机无穷大系统为例（如图1所示），通过分析装有 SSSC系统 Phillips -Heffron 模型，可以得到 SSSC 提供的附加阻尼转矩。

图1 装有 SSSC 的单机无穷大系统结构图

图1 中，US为无穷大系统母线电压，Ut为发电机机端电压，SSSC安装在输电线路中间，它对系统的贡献等效成一个幅值和相位可以变化的电压源Usc与耦合变压器的漏抗xsc串联而成。根据发电机非线性方程[6]、SSSC的动态模型以及SSSC 对整个系统提供的附加转矩计算[7]，可以得到安装有SSSC的单机无穷大系统的Phillips-Heffron模型见图2。回路，第三部分为虚框部分，其输出体现了SSSC对系统提供的附加转矩。图中，δ为电角度；ω为电角速度；Mt为原动机机械转矩，Me2为发电机及其励磁系统提供的电磁转矩，m、 δ sc分别是逆变器幅值调制系数和SSSC 注入电压相角。其他参数及系数K1～K6的意义见文献[5]。

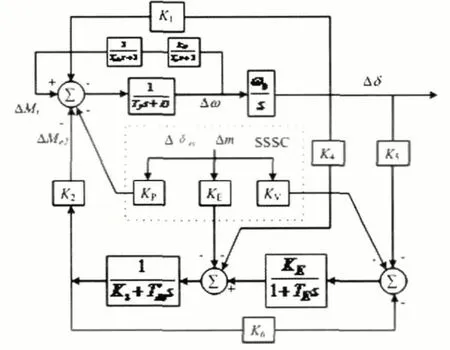
图2 含SSSC的扩展Phillips-Heffron模型

SSSC控制器提供的附加转矩分别来源于幅值调制系数Δm和 SSSC 注入电压相角Δδsc对系统的影响。附加转矩可以分成两部分。第一部分称为直接阻尼转矩，它通过KP加入到发电机惯性环节，参数[KPmKPδ]用来表征其影响程度；第二部分称为间接电磁转矩，其大小受到KE([KEmKEδ])、KV([KVmKVδ])的影响，相对于直接转矩，间接转矩受到了发电机及其励磁系统回路的影响，由于间接转矩被励磁绕组及同步发电机惯性环节削弱，这部分转矩的大小比直接转矩小很多，因此，SSSC产生的附加电磁转矩主要受到直接阻尼转矩的影响，即：

在SSSC调节控制潮流的过程中，输出电压相角的变化δsc作用主要是稳定直流侧电容电压在参考值。Δδsc的变化很小，对系统的影响可以忽略不计。所以SSSC对系统阻尼转矩的影响主要来自于逆变器幅值调制比的变化Δm 对系统的贡献。故Δm的控制规律决定了SSSC对系统阻尼水平的影响。为了有效的抑制系统的频率大幅波动，需要分析SSSC的控制规律并设定合理的控制器参数。

2 SSSC 的控制规律的讨论及参数整定

2.1 SSSC控制规律（阻尼控制器）的讨论

用于稳定控制研究的常用的SSSC阻尼控制器模型如图3所示。由图可见，控制器的输出信号mSSSC由两部分组成：SSSC的电压幅值调制比参考值mSSSC0与偏差信号mSSSC。所设计控制器的相位补偿环节由滤波器和超前滞后环节所构成。

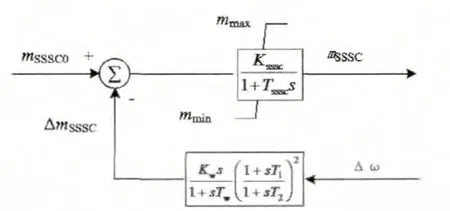
图3 SSSC阻尼控制器模型

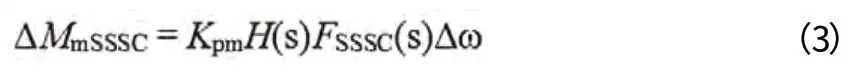
其中：H(s)代表SSSC相位补偿环节传递函数，Fsssc(s)代表自身响应延迟环节。

2.2 相位补偿原理设计SSSC阻尼环节参数

相位补偿法[4]是在频域下用于整定阻尼控制器参数的方法。理想的SSSC装置将为系统提供纯正向阻尼转矩，即完全相位补偿。SSSC控制器参数按照如下方法整定。

其中：ωn为转子无阻尼自然振荡角频率[6]，由式（4）算出两级超前滞后环节的角度φ，每级补偿φ/2，则由超前-滞后环节基本公式[8]可获得参数：

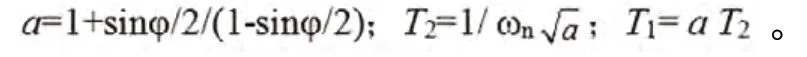
设希望加入SSSC阻尼控制器后，转子振荡的阻尼比为ξ x（0.1～0.3）：

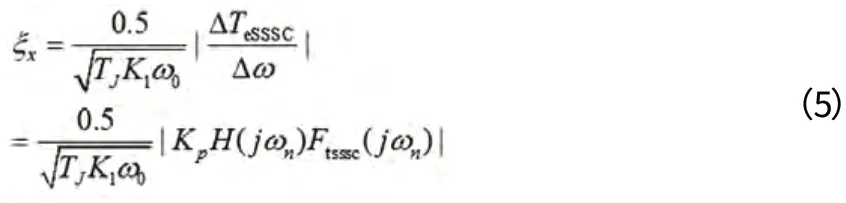
式（4）～（5）就是利用相位补偿原理整定SSSC装置参数的公式。

3 SSSC控制器参数整定的具体步骤

1）由潮流计算获得系统初始运行工况，并计算其他状态量初值。

3）计算全部特征根及其特征向量υi、μi。

4）提取特征根中的机电振荡模式λi，并计算振荡模式的灵敏度

4 仿真算例分析

两机系统网络结构图如图4所示。图中G1为汽轮发电机，G2为水轮发电机，SSSC安装在联络线上，这样可以向联络线两端的机组分别提供一定的阻尼。水轮发电机采用3阶模型，汽轮发电机采用4阶模型，励磁系统、调速器都采用典型参数[6]。

图4 两机系统网络结构图

将潮流计算的结果作为暂态计算的初值。根据第2节控制器设计方法，SSSC的容量S=100Mvar，直流电容电压Vdc=40kV，Cdc=375μF。根据特征根灵敏度计算，转子无阻尼自然振荡角频率ωn=7.7799；按照SSSC控制器环节相位整定公式（4）可以得到，超前-滞后环节需要补偿的角度为φ=0.3646，从而得到超前滞后环节中的时间常数T1，T2，计算公式如下：

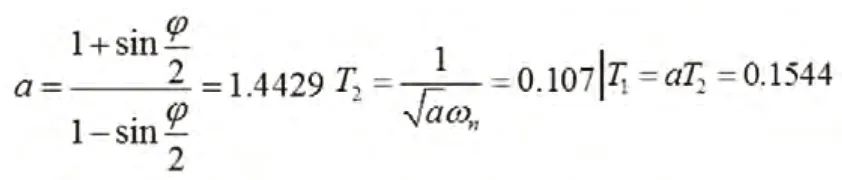
设加入SSSC阻尼控制器后，稳定器提供的阻尼比达到ξ=0.3，再根据式(5)得到阻尼控制器增益Kw=51.6474，控制器的其他参数均取典型参数（Tw=20，KSSSC=4；TSSSC=0.02），至此，SSSC阻尼控制器的参数整定完毕。

算例1：分析机组参考开度的变化对机组频率及联络线功率稳定性的影响。在5s时，将3号机组的给定开度减少0.24，4号机组给定开度增加0.24。仿真结果如图5～6所示。

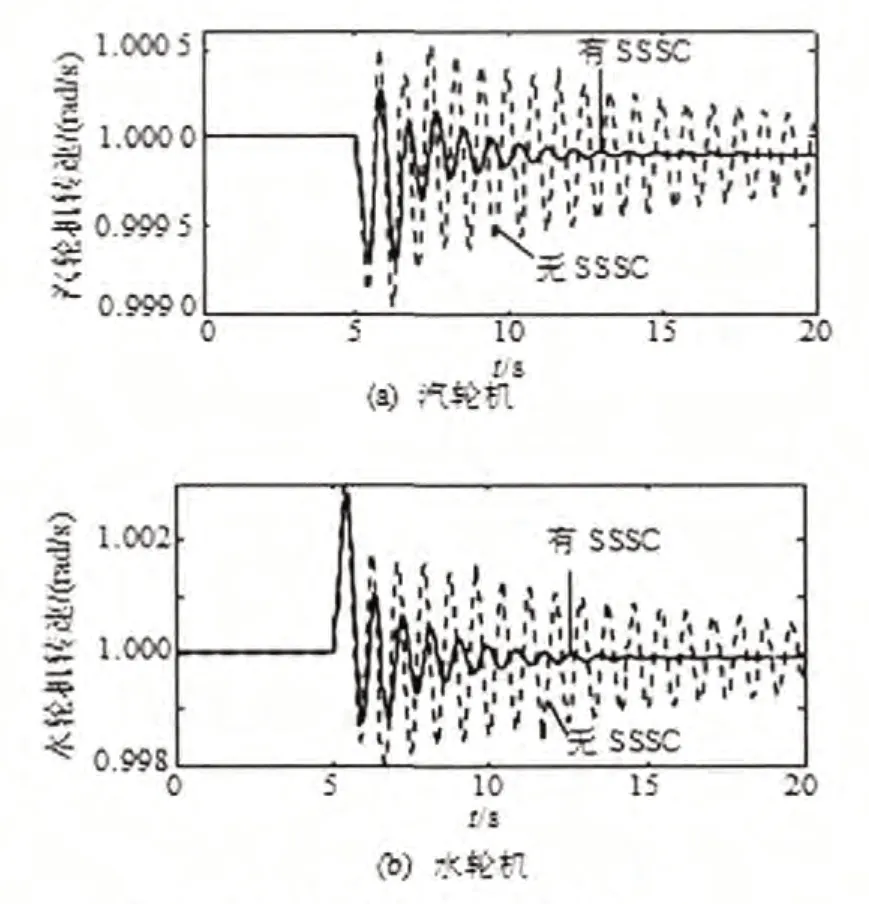
图5 算例1下各机组频率仿真结果

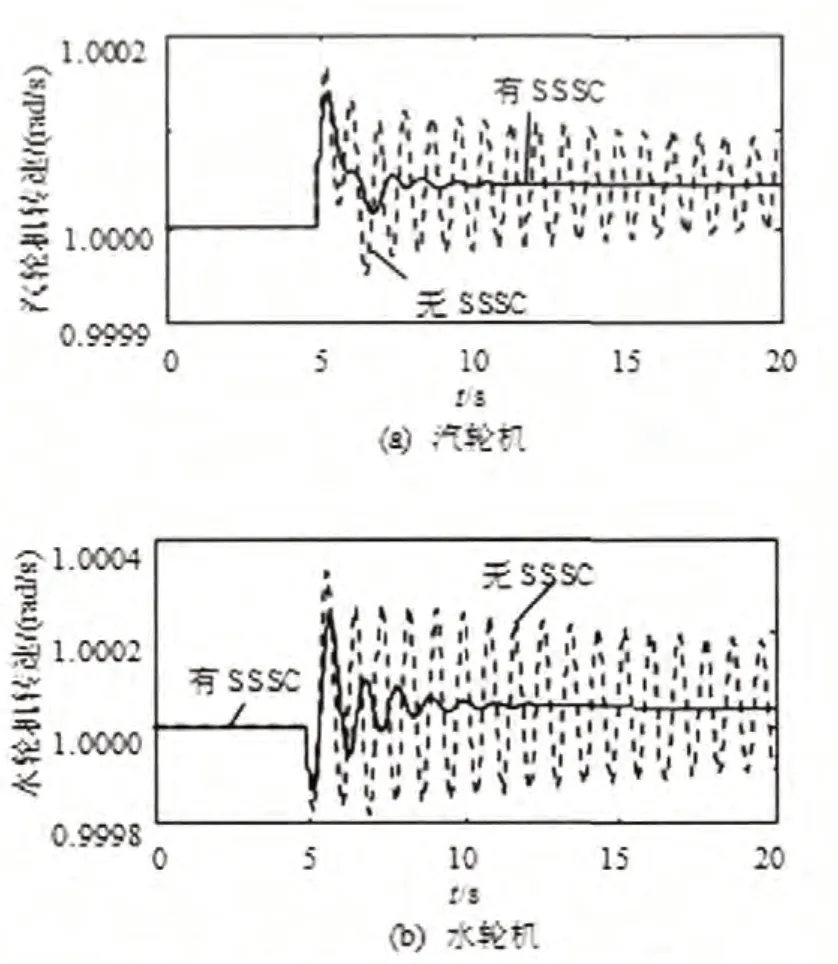
图7 算例2下各机组频率仿真结果

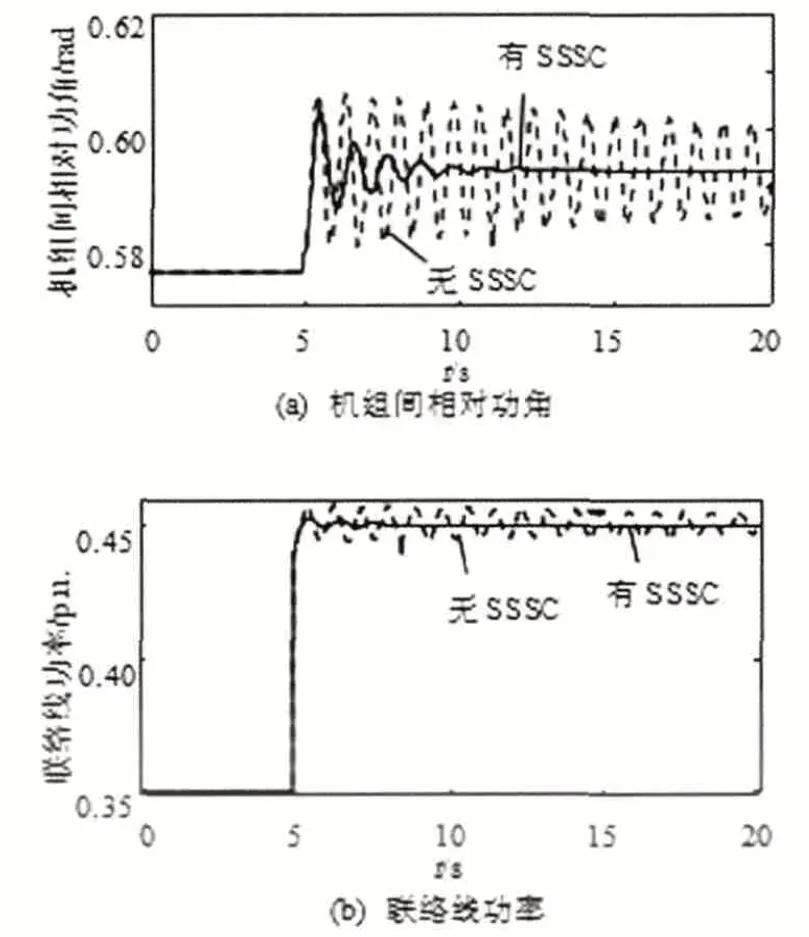
图8 算例2下机组间相对功角及联络线功率仿真结果

算例2：分析负荷波动对机组频率及联络线功率稳定性的影响，在5 s时将母线1、2的有功负荷分别变化0.12，仿真曲线如图7～8所示。

由此可见，当系统发生机组出力波动及负荷扰动时，机组频率、机组间相对功角及联络线功率在安装SSSC前后都发生了很大的变化，安装后，由于受到SSSC的阻尼作用使机组频率和相对功角波动得到了有效的抑制。

5 结束语

针对有功功率扰动所引发的频率及联络线功率大幅波动现象，本文介绍了静止同步串联补偿器（SSSC）的阻尼作用，并通过引入Phillips-Heffron 模型及其SSSC对系统阻尼转矩的贡献，讨论了SSSC的控制规律并引入了阻尼传递函数模型，为给系统提供有效的阻尼，根据特征根分析法及相位补偿法完成了控制器的参数整定。仿真结果验证了整定参数后的SSSC能够有效抑制有功功率扰动引起的频率大幅波动现象。

[1]吴俊玲.大型风电场并网运行的若干技术问题研究[D].北京:清华大学，2004．

[2]方思立,朱方.电力系统稳定器(PSS)在世界各地的使用情况[J].电网技术,1994,18(2):15-19．

[3]Issarachai Ngamroo.Application of static synchronous series compensator (SSSC) to stabilization of frequency oscillations in an interconnected power system.[J].Circuits and Systems,2001,2 (2):113-116．

[4]Wang H F，Swift F J．A unified model for analysis of FACTS devices in damping power system oscillations Part I：Single-machine infinite-bus power system[J].IEEE Trans on Power Systems,1997,12(2):941-946．

[5]刘取.电力系统稳定性及发电机励磁控制[M].北京:中国电力出版社,2007．

[6]倪以信,陈寿孙,张宝霖,等.动态电力系统的理论和分析[M].北京:清华大学出版社,2002．

[7]郭成,李群湛.基于改进PSO算法的SSSC广域阻尼控制器设计.电工技术学报,2010,25(1):151-158．

[8]夏德钤,翁贻方.自动控制理论[M].北京:机械工业出版社,2007．