复杂局部地形中的实时路径规划算法设计

周自维，李长乐，赵 杰，徐望宝

复杂局部地形中的实时路径规划算法设计

周自维1，2，李长乐1，赵 杰1，徐望宝2

（1.哈尔滨工业大学机器人研究所，150001哈尔滨；2.辽宁科技大学电子信息工程学院，114000辽宁鞍山）

针对复杂局部环境中机器人实时自主导航问题，设计了“双向搜索多边形构造算法”和“基于势场函数的机器人运动控制器”.“双向搜索多边形构造算法”能够在机器人被障碍物包围的环境下搜索出障碍物的包围多边形，从而获取基于障碍的最优行进路径；“基于势场函数的机器人运动控制器”是一个多变量控制器，输入矢量由吸引势场函数和排斥势场函数组成，输出矢量由速度和转角组成，该控制器控制机器人实际运动，使机器人能够有效躲避障碍物并逐步趋向目标点；控制器还设定了机器人运动的基本速度，解决势场为零时引起的局部极小化问题.与“沿墙走算法”、“人工势场法”等方法的实验比较表明，本文算法能够获得更好的优化性和实时性，具有更加广泛的实际应用范围.

路径规划；局部最优；运动控制器；自主导航；沿墙走算法

复杂二维环境中的机器人实时自主导航的研究划分为两大类，一类是基于静态环境的全局优化研究，另一类是基于传感器数据的局部优化研究［1-2］.静态全局优化方法不但需要很大的存储空间，而且需要耗费较长的计算时间，因此该类问题能够求解的数据空间范围和精度以及求解的实时性会有较大限制［3-4］，同时静态全局问题对于机器人面临的不断变化的环境信息、随时可能出现的移动障碍，甚至机器人自身不断变化的参数都不具有良好适应性.虽然文献［5］提出了重新规划的方法，但是不断重新规划的策略无疑也增加了机器人额外的处理时间.另一类针对机器人传感器信息的局部规划算法中，人工势场法（artificial potential field）［6-8］在解决局部规划中发挥了重要作用.但是人工势场法有其特定的缺陷即局部最小点问题，或者称为局部陷阱问题.为解决该问题，科研人员提出一些新的势场函数，例如超二次方程势场法［9］，协调函数法［10］，人工力矩算法［11-12］等，还有些方法试图改善障碍物的表达方式，比如虚拟障碍的方法［13-14］子目标法［15-16］等，但是上述方法仍然没有从根本上消除人工势场法固有缺陷.沿墙走算法（wall⁃following or Bug method）［17-19］以及改进算法［20-21］在逃离局部陷阱的方面做了新的尝试，新算法试图控制机器人始终沿着障碍物边缘的一个方向运动，从而脱离局部陷阱，但是这些方法对可通行路径的优化考虑较少，因而有进一步改善空间.

本文提出一种新的基于传感器数据的实时路径优化算法.算法的设计分为两个步骤，1）采用“双向搜索多边形构造算法”，搜索出复杂障碍物的包围多边形，然后以包围多边形顶点构造基于障碍物和机器人关系的可视图，并以可视图为基础进行路径优化.与传统的凸包算法［22-23］相比，本文构造算法的复杂度为O（K lg N），N为障碍物点数，K为包围多边形顶点数，小于传统凸包算法复杂度.2）设计了“基于势场函数的机器人运动控制器”.当机器人的最终目标不被障碍物阻挡，直接将该最终目标定义为控制器目标点，否则机器人从障碍物可视图中计算最优行进路径，以最优行进路径上的第一个节点为趋近目标，将其命名为“当前目标”.控制器设计中，目标点（最终目标或者当前目标）对机器人产生吸引势，障碍物对机器人产生排斥势，机器人以吸引势和排斥势构成矢量和为输入条件，根据机器人自身状态计算出机器人行进的速度和转角，在该输出控制下调整自身姿态，从而躲避障碍物走向目标点.同时控制器设置了“基本速度”，具备非常好的逃离局部陷阱的能力.

1 基本概念、定义与假设条件

为了将本文算法描述清楚，首先做如下定义：定义从点p1到p2的有向线段为l（p1，p2），有向线段的角度定义为βl，同时βl应该满足条件-π＜βl≤π，有向线段的长度定义为Dis（l（p1，p2））.一个二值函数ξ（x）定义为

其中sgn（x）是变量X的符号函数.

函数d gl（x）定义为d g l（x）函数将x的角度范围定义在（-π，π］.

如果βi和βj分别是有向线段li和lj的方向角，那么有向线段li到有向线段lj之间的夹角就定义为βij，使用上述定义的函数，夹角表示为βij＝d g l（βi-βj）.

定义1 障碍物模型

定义点集合G［k］＝P（g1…gk），其中g1…gk是机器人获取的障碍物点.任意两个相邻的边缘点gi、gi＋1之间的距离需要满足如下条件：

其中min GP和max GP是预先定义的相邻障碍点的最小和最大距离.假设机器人扫描到障碍点g1…gk后，机器人就能够存这些障碍点，并且将这些信息作为机器人对障碍物的已知信息.

本文算法所适应环境是具有移动障碍物的复杂二维环境，由于一个控制周期以毫秒为计量单位，因此假设在一个控制周期内，扫描到的障碍物位置没有发生变化，另外还假设无论当前的二维工作环境多复杂，总存在一条从机器人到达目标点的可行路线，否则该路径规划算法无法发挥作用.最后假设机器人能够定位自身位置和要到达的最终目标的位置，上述假设，无论是面对理论要求还是真实实验环境，都是能够实现且比较合理的.

2 基于局部复杂障碍的路径优化算法

2.1双向搜索多边形构造算法描述

该构造算法总是试图寻找障碍物的突起点，因为突起点是障碍物中一部分区域的代表点，包围障碍物的多边形就是由障碍物的多个凸起点组成［24］.

对于障碍点，首先利用凸包算法［25-26］构造障碍区域轮廓，获得障碍边缘GL［n］.根据机器人R和目标T生成线段l（R，T），判断l（R，T）和障碍物GL［n］是否相交，如果不相交，则说明障碍物G没有处在机器人R和目标点T之间，最短路径就是机器人R和目标T之间的连线；如果相交，则说明障碍物阻挡了机器人R走向目标T，显然这时机器人不能直接走向目标点.在该条件下用l（R，T）将障碍物分为两部分，分别命名为“顺时针部分“和”逆时针部分”，以“顺时针部分”为例描述算法的构造顺序.

将线段l（R，T）和障碍GL［n］的交点命名为PC，并且以顺时针方向沿着“顺时针部分”的边缘移动PC，把这条搜索路线定义为“正向搜索线”如图1所示.沿此路线，每当PC点移动一步，就判断l（PC，T）和障碍线GL［n］是否相交，如果相交，则继续沿着“正向搜索线”移动PC点，直到PC点移动到一个能够和目标T直接相联的位置，如图1中位置T1，这时记录下T1的位置.定义该点为“目标最近点”.

图1 双向搜索多边形生成算法示意图

总之，在所有的能够直接到达目标点T而不被障碍物G所阻碍的位置点中，“目标最近点”是距目标点T的距离最小的一个点（这里只考虑“顺时针部分”障碍）.

算法的下一步骤是继续搜索包围障碍物多边形的其他顶点.在下一步的搜索过程中，反过来以T1为起始点，以机器人R为搜索的目标点.计算线段l（T1，R）和障碍GL［n］的“顺时针部分”是否相交，如果相交，记录交点为PC，并让PC沿着“反向搜索线”移动，每移动一步判断l（PC，R）和障碍GL［n］的“顺时针部分”是否相交，如果相交就将交点PC继续沿“反向搜索线”移动，直到PC点能够直接和机器人R联通，这时PC点处于R1所在位置，如图1所示.命名该点为“起始最近点”.可以看出，“起始最近点”是所有从T1开始，越过障碍G寻找机器人R位置的所有点中，距离机器人R最小的一个点.（同样这里也只考虑“顺时针部分”的障碍）.通过上述描述可以做如下假设，如果存在一条从机器人R到达目标T，并且绕过障碍物G的多边形，尽管还不能找出这条多边形的全部节点，但是“目标最近点”和“起始最近点”一定在这条多边形上，而且这两个点分别是该多边形的头点和尾点.由于这条预期多边形的头和尾已经找到，再以头尾开始，继续向中间收敛，那么这个逆时针部分的多边形就能够全部搜索出来.因此，重新以R1开始，以T1为目标，重复上述搜索过程，会继续得到包围障碍物多边形的另一组节点，继续命名为R2、T2.重复上述正向、反向搜索过程，直到起始点和终止点位置重合，就找到了包围障碍物边缘的多边形的所有点位置（顺时针部分），如图1所示的线路2.由于每次搜索都是以正向搜索／反向搜索为基本步骤，因此该算法命名为“双向搜索多边形构造算法”.在搜索过程中，每次搜索出来的节点都被用作下一次搜索的初始点，每个搜索出来的节点的信息都得到充分的利用，因此冗余计算少，算法简洁，收敛速度快，实时性好.

“逆时针部分”的搜索过程，和“顺时针部分”的搜索过程类似，最终得到的包围多边形如图1所示的线路1.

2.2多边形构造算法伪代码

双向搜索多边形构造算法：

Step 1 根据机器人R、障碍物T生成线段l（R，T），计算线段l（R，T）和障碍物GL［N］的交点，如果l（R，T）和障碍GL［n］不相交，则算法结束，说明障碍物没有阻碍机器人走向目标点.否则记录交点为PC，并按照障碍物正向部分生成“正向搜索线”和“反向搜索路线”，同时生成两条路线F ront-R oute［n］和A pposite-Route［n］，并清空这两条路线.

Step 2 沿“正向搜索线”移动交点PC，每次移动PC后，判断l（PC，T）和障碍线GL［n］是否相交.如果相交，返回Step 2.否则将PC插入路径F ront-Route［n］头部，设置机器人R为目标点，生成线段l（PC，R）

Step 3 沿“反向搜索线”移动点PC，每次移动PC后，判断l（PC，R）是否和GL［n］相交.如果相交，返回Step3，否则，将PC点插入路径A pposite-R ou te［n］的尾部.

Step 4 如果点F ront-R ou te［n］和点A pposite-R ou te［n］位置相等，跳转到下一步.否则设置F ront-R oute［n］为目标点T，A pposite-R ou te［n］为起始点R，并返回至Step 2.

Step 5 设置Fron t-R ou te［n］为“目标最近点”，A pposite-R oute［n］为“起始最近点”，连接路径A pposite-Route［n］和Front-R ou te［n］为一条路径，并命名为ClockMinRoute，算法结束.

通过算法上述步骤得到包围障碍物的多边形，同时该多边形将机器人隔离在障碍物之外.

2.3基于可视图的最短路径搜索算法

Dijkstra算法［23］是对网络可视图进行最短路径寻优的基础算法，该算法能够搜索出一个可视图中各个顶点距离指定顶点的最短距离，同时该算法收敛速度快，具有良好的实时效果.在前一节中，本文所述的“双向搜索多边形构造算法”搜索出了包围复杂障碍物的凸多边形，利用该凸多边形可构造描述障碍物的“可视图”.有了可视图之后，采用Dijkstra最优搜索算法，就可以得到通过障碍物的理论最短路径.算法的基本过程和证明参考文献［23］，Dijkstra算法的时间复杂度为O（N2），N为顶点数.

3 基于势函数的机器人运动控制器设计

前节算法虽然搜索出了从机器人到障碍物的最短路径，但是最短路径的获取是通过用障碍物包围多边形构造的可视图，并在可视图基础上采用Dijkstra算法求得，其最优的概念是针对障碍物的最优.而实际的机器人运动是机器人自身的运动，因此机器人实际的行走路线需要以最优路径为目标进行自我调整.在最优路径的构造中机器人自身参数并未考虑在优化之内，否则优化算法复杂性将大大增加.局部最优路径是基于瞬时局部障碍信息，而实际机器人的运动是连贯不断的过程，在机器人运动期间，“可视图”信息将不断变化，因此最优路径是机器人运动的预期和近似，实际的机器人具备自身物理尺寸和安全距离（如定义1所描述），其行进路线不可能和最优路线一致，而是尽量贴近最优路线.

针对上述描述设计机器人运动控制器，该控制器以目标点和障碍物对机器人的吸引势和排斥势做为输入矢量，以机器人运动的速度和方向为输出矢量，进而控制机器人的整体运动.在控制器设计中，为保证机器人能够运动到最终位置，定义机器人的目标T为机器人的“最终目标”，如果机器人无法直接到达“最终目标”T，则将首先能够到达的最优路径上的第一个顶点定义为趋近目标，并将其命名为机器人的“当前目标”，每个控制周期内，最短路径搜索算法都会提供机器人一个“当前目标”，不断指引机器人向最终目标前进.

控制器的设计还保证即便发生吸引势与排斥势的和为零的情况发生，机器人仍会以一个基本速度运动，这样即使机器人处于零势场空间，仍然能够在“当前目标”的指引作用下脱离局部陷阱.同文献［12，24，27］中的定义相比，该运动控制器所采用的参数具有明确简洁的物理意义，因而在最后的实验中能够更好地体现控制器算法的效果.

控制器设计基本步骤介绍如下：

机器人半径为Dr，机器人安全距离为Ds，机器人方向角为βR，机器人要达到的目标位置定义为T，βRT为机器人和目标点之间的夹角，而βTR是目标点和机器人之间的夹角.

归一化函数amt（x）的定义如下：

其中sgn（x）表示变量x的标号函数，δθ表示一个远远小于π／2的角度，表达为δθ≪π／2，该函数是一个归一化函数，体现了变量x在零点附近集中的程度.

吸引势函数：

1）当“当前目标”T不是机器人的最终位目标时，吸引势函数定义为

吸引势函数表达了机器人目标点对机器人的吸引作用.函数值的大小由βR（k）-βRT（k）决定，其中βRT（k）是有向线段l（T，R）的方向，βR（k）-βRT（k）是有向线段l（T，R）和机器人方向的夹角.该函数表达了当目标T在机器人后方时，其吸引势函数对机器人角度取值最大，机器人会尽可能转向目标T.而当目标在机器人前进方向时则机器人角度不变，直接走向目标T，因而目标对机器人角度的吸引势较弱.其中λa为一个常量，通过设计的实验的结果分析，当λa＝0.55时，函数较好的体现了目标对机器人的吸引作用.

2）当“当前目标”T是机器人最终目标时，吸引势函数定义为

该吸引势函数仍旧由βR（k）-βRT（k）决定，但是由于最终目标具有方向βT，因而函数在运动方向上有所变化，其目的是期望当机器人到达最终目标点时位置不但要和最终目标的位置一致，方向也尽可能接近最终目标点方向，如果“当前目标”T不是最终目标，则不需要考虑目标T的方向问题.同时该函数也使得机器人到达最终目标后，不会震荡，而是稳定的靠近目标位置.

排斥势函数：

排斥势函数体现了机器人安全半径内的障碍物对机器人的排斥作用，通过障碍物的排斥作用迫使机器人远离障碍物.排斥势函数的定义为其中λp＝（Ds-DGR）／Ds.

可以看到，排斥势函数是多个障碍物点Gi对机器人排斥作用的代数和.排斥势函数的大小由（βR（k）-βGi，R（k））决定，βGi，R（k）是有向线段l（Gi，R）的夹角.当（βR（k）-βGi，R（k））最小时，说明障碍物处在背对机器人的位置，因此障碍物对机器人排斥势能较低，当（βR（k）-βGi，R（k））最大时，说明障碍物处在机器人运动方向的前方，因而障碍物会用较大的势能推动机器人转向，使得机器人及时躲开障碍物.

根据以上吸引势函数和排斥势函数，机器人运动控制器的递推方式定义如下：

梯度函数定义为

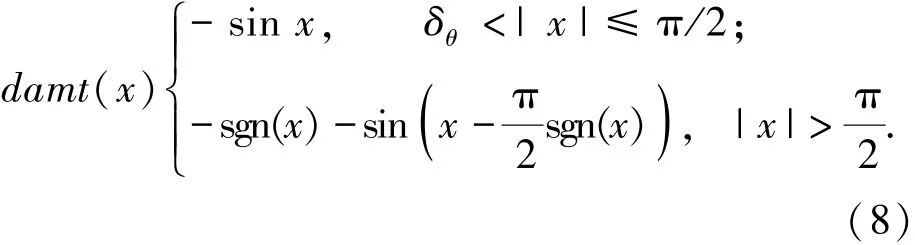
结合式（1）～（8），可得

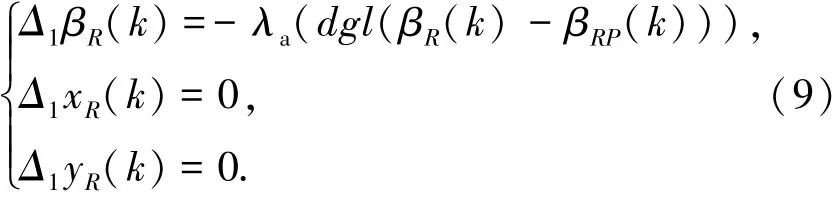
式（9）是吸引势函数的调整结果.

如果机器人的“当前目标”和机器人的最终目标一致，那么结合式（1）～（9），有

结合式（10）排斥势能产生的控制步长，

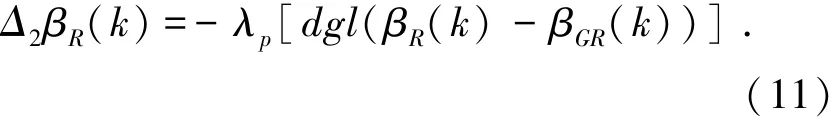
式（11）中，Δ2βR（k）表示由各个障碍物对机器人产生的排斥势能的代数和.

机器人实际步长函数Sx（k）和Sy（k）定义为

其中SR是机器人行走的最大步长.

从上述分析可知，控制器的每个参数都有明确的物理意义，因此该控制器算法清楚，并且适合实际的机器控制.

4 实验与分析

为了验证本文提出算法的有效性，设计了两个实验，机器和环境参数设置见表1.

表1 机器人和障碍参数设置像素

在实验1中，采用两类人工障碍物（即手动设定的障碍点）：第一类人工障碍简单但是障碍物的数目较多；第二类人工障碍物为复杂的螺旋形障碍，并且机器人的初始和目标位置都处于螺旋障碍物环抱中间.实验的程序采用Visual Studio 6.0平台的C＋＋程序设计，能体现算法的实时性和实际应用价值.图2给出了第一类人工障碍环境中，本文算法同“人工力矩法”和“沿墙走算法”行走路径的对比示意图，其具体结果见表2.

图2 第一类人工障碍中不同算法的规划结果

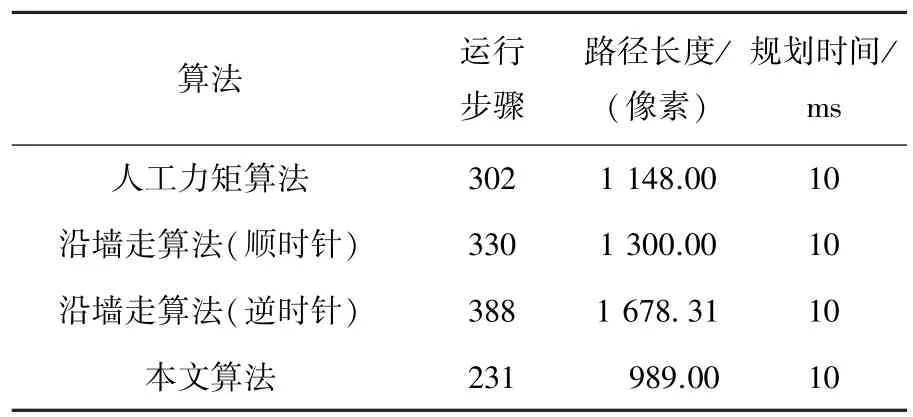
表2 人工障碍1中的实验对比结果

从表2和图2中可以看到，本文得到路径结果最短，步数最少，体现了本文最优路径规划的有效性，机器人行走的轨迹平滑，体现了运动控制器良好的控制效果，控制时间也保证了算法的实时性.

实验2中采用AS-R轮式机器人，该机器人由3部分组成，分别是“传感器模块”、“中央控制模块”和“运动执行模块”.“传感器模块”由红外和声纳传感器组成，沿机器人圆周排布着8个声纳传感器和8个红外传感器.声纳传感器和红外传感器分别以π／4角度互相排列，红外传感器的最佳探测距离为0.3～0.9 m，声纳传感器的最佳探测距离为0.6～4.0 m，这两类传感器覆盖了从远到近的探测范围.“中央控制模块”由计算机和PCI总线的传感器接口卡、运动控制卡组成.计算机基于Windows系统运行，整个开发和测试平台采用Visual Studio6.0开发.“运动执行模块”由电机驱动器、两个驱动轮、一个辅助轮和电池组成.驱动轮采用闭环控制，位置反馈采用2 000线码盘，精度足够满足实验需求，电池充满电后能够满足2 h的工作时间.采用VC6.0开发的测试平台能够完成位置传感器控制、电机控制、摄像机和无线网络控制功能，保证机器人处于良好的工作状态，同时提供了用户开发程序接口.实验2中，针对机器人的运动，设计了两种运动模式，分别是直行模式和转弯模式.直行模式中，双轮同速同向运动，机器人行走的距离就是双轮转过的周长；转弯模式中，双轮反向同速运动.机器人转动的弧度δ＝（α∗R）／r，其中R是机器人轮半径，r是机器人半径，α是轮转过的弧度.设机器人位置（Xr，Yr），机器人角度为βR，传感器与机器人正向夹角为α，障碍点返回距离为ddis，则障碍物位置（Xo，Yo）的计算公式为

实验2中每个控制周期为20 ms，根据机器人实际的运动速度要求，本文算法能够比较好的满足实时性的要求，图3（a）中是实验所用机器人，图3（b）中机器人向目标运动，当有障碍进入机器人安全半径，机器人及时转弯以避免碰撞（见图3（c）），并选择除了可通行路径如图3（d）、图3（e）所示，最后达到设定位置如图3（f）所示.为验证实际应用中机器人躲避移动障碍物的能力，在实验2中添加了一个障碍机器人如图4所示.试验中两个机器人互为障碍，该实验不但能够体现机器人躲避移动障碍物的能力，而且很好地体现机器人检测移动障碍能力.实验2的结果见表3.其中控制周期的时间包括：机器人对障碍检测时间、路径优化时间和势函数控制器迭代运算时间.

图3 单机器人在实际障碍中避碰与规划

图4 两个移动机器人相互避让实验

表3 实验2中实际机器人运动数据对比结果

由表3可知，本文算法在实际机器人应用中体现了良好的优化和控制效果.

5 结 论

1）提出了“双向搜索多边形构造算法”，根据机器人扫描到的障碍点生成障碍物包围多边形.该多边形构造算法使得机器人在处于被障碍物包围的情况搜索出绕过障碍物的可行路径，并在基于多边形基础的可视图中求取最优路径.

2）设计了基于吸引势和排斥势的机器人运动控制器，控制器在已获得最优路径的前提下，不断用优化目标引导机器人脱离障碍，走向最终目标，同时控制器的“基本速度”保证机器人不会停在零势场范围内.

3）本文算法无论在人工地图中还是在实际机器人应用中都能对复杂障碍物有很好的通过能力，能够有效脱离复杂螺旋形障碍物的包围，并对行走的路径有优化能力，保证机器人行进路线稳定、平滑.和其他算法如人工势场法、沿墙走算法比较，本文算法规划能力强，实时性好，具备广泛的应用前景.

［1］UNDEGER C，POLAT F.Real⁃time edge follow：a real⁃time path search approach［J］.IEEE Transactions on Systems，Man and Cybernetics⁃Part C：Application and Reviews，2007，37（1）：860-872.

［2］JANABI⁃SHARIFI F，WILSON W J.A fast approach for robot motion planning［J］.Journal of Intelligent and Robotic Systems，1999，12（25）：187-212.

［3］MINGUEZ J，MONTANO L.Nearness diagram（ND）navigation：collision avoidance in troublesome scenarios［J］.IEEE Trans Robot Automat，2004，20（1）：45-59.

［4］MINGUEZ J，MONTANO L.Sensor⁃based robotmotion generation in unknown，dynamic and troublesomescenarios［J］.Robot Autonomous Syst，2005，52（1）：290-311.

［5］STENTZ A，HEBERT M.A complete navigation，system for goal acquisition in unknown environments［J］.Autonomous Robots，1995，2（2）：127-145.

［6］RIMON E，KODITSCHEK D E.Exact robot navigation using artificial potential functions［J］.IEEE Transactions on Robotics and Automation，1992，8（5）：501-518.

［7］GE S S，CUI Y J.Now potential functions for mobile robot path planning［J］.IEEE Trans on Robotics and Automation，2000，16（5）：615-620.

［8］KIM D H.Escaping route method for a trap situation in local path planning［J］.International Journal of Control Automation and Systems，2009，7（3）：495-500.

［9］VOLPE R，KHOSLA P.Manipulator control with super quadric artificial potential functions：theory and experiments［J］.IEEE Transactions on Systems，Man，and Cybernetics，2000，20（6）：1423-1436.

［10］VASCAK J.Navigation of mobile robots using potential fields and computational intelligence means［J］.Acta Polytechnica Hungarica，2007，4（1）：63-74.

［11］XU Wangbao，CHEN Xuebo.Artificial moment method for swarm-robot formation control［J］.Science in China⁃Series F：Information Science，2008，51（10）：1521-1531.

［12］XU Wangbao，CHEN Xuebo.A dynamical formation control approach based on artificial moments［J］.Control Theory＆Applications（in Chinese），2009，26（11）：1232-1238.

［13］PARK M G，LEE M C.A new technique to escape local minimum in artificial potential field based path planning［J］.KSME International Journal，2003，17（12）：1876-1885.

［14］PARK M G，LEE M C，SON K.Real⁃time path planning in unknown environments using a virtual hill［C］／／Proceeding of the 16th IFAC Word Congress.Laxenburg，Astralia：IFAC Secretariat，2005：61-65.

［15］BELL G，WEIR M.Forward chaining for robot and agent navigation using potential fields［C］／／Proceedings of the 27th Australasian Computer Science Conference.New Zealand：Australian Computer Society，2004：265-274.

［16］WEIR M，BUCK A，LEWIS J.A mind’s eye approach to providing BUG⁃like guarantees for adaptive obstacle navigation using dynamic potential fields［J］.Lecture Notes in Computer Science，2006，4095：239-250.

［17］YUN X P，TAN K C.Wall⁃following method for escaping local minima in potential field based motion planning［C］／／Proceedings of the International Conference on Advanced Robotics’97.Piscataway，NJ，United States：IEEE，1997：421-426.

［18］JAMES N，THOMAS B.Performance comparison of bug navigation algorithms［J］.Journal of Intelligent and Robotic Systems，2007，50（1）：73-84.

［19］MABROUK M H，MCLNNES C R.An emergent wall following behaviour to escape local minima for swarms of agents［J］.International Journal of Computer，2008，35（4）：463-76.

［20］JAVIER A，ALBERTO O，JAVIER M.A bug⁃inspired algorithm for efficient anytime path planning［C］／／2009 IEEE／RSJ International Conference on Intelligent Robots and Systems.St.Louis：IEEE Robotics and Automation Society，2009：5407-5413.

［21］ZHU Yi，ZHANG Tao，SONG Jingyan.A new bug⁃type navigation algorithm for mobile robots in unknown environments containing moving obstacles［J］.Industrial Robot：An International Journal，2012，39（1）：27-39.

［22］GRAHAM R L.An efficient algorithm for determining the convex hull of a finite planar set［J］.Information Processing Letter，1986，31（1）：132-134.

［23］THOMAS H，CORMEN，CHARLES E，et al.Introduction to Algorithms［M］.Second Edition.New York：MIT Press and McGraw⁃Hill，2011：955-956.

［24］ZHAO Jie，ZHOU Ziwei，LI Ge，et al.The apposite way path planning algorithm based on local message［C］／／2012 IEEE International Conference on Mechatronics and Automation.Washington D C，United States：IEEE，2012：1563-1568.

［25］TOUSSAINT G T.Solving geometric problems with the rotating calipers［C］／／Proceedings of IEEE MELECON.New York：IEEE，1983.

［26］戴光明，杜安红.壁障问题最短路径的两级动态规划算法［J］.华中科技大学学报：自然科学版，2006，34（3）：122-124.

［27］CHANG Y C，YAMAMOTO Y.Path planning of wheeled mobile robot with simultaneous free space locating capability［J］.Intel Serv Robot，2009，2（1）：9-22.

（编辑杨 波）

A real time path planning algorithm based on local complicated environment

ZHOU Ziwei1，2，LI Changle1，ZHAO Jie1，XU Wangbao2
（1.State Key Laboratory of Robotic and System，Harbin Institute of Technology，150001 Harbin，China；2.School of Electronics＆Information Engineering，Liaoning University of Science and Technology，114000 Anshan，Liaoning，China）

A novel algorithm，which comprises with convex hull construction algorithm and robot controller is proposed for robot path planning based on complicated local data in robot’s autonomous navigation system.First the algorithm searches out the local optimal path from the robot’s current position to its target according to the localobstacle data.When the robotcan notreach the finaltargetdirectly，a temporary targetpointin the optimal path will be set to instruct the robot to avoid the obstacle and reach the final target.Next，a controller is design based on attractive force field and repulsive force field to control the robot’s motion，the combined effect of both attractive force field and repulsive force field drives the robot move toward the objective acquired from the optimal path and avoid obstacles at the same time.The experiment results show that this method can provide a better planning path compared with traditional path planning algorithms such as artificial potential field（APF），the wall⁃following（Bug）and the artificialmomentmethod，and ithas a fast reaction speed that is suitable for practical applications.

path planning；local optimal；motion controller；autonomous navigation；wall⁃following

TH137

A

0367-6234（2014）08-0065-07

2013-05-04.

国家自然科学基金资助项目（51105101）.

周自维（1974—），男，博士，讲师；

赵 杰（1968—），男，教授，博士生导师.

李长乐，8561388＠qq.com.