运费无差异的多品种流交通网络最小费用算法

寇玮华，崔皓莹

(西南交通大学交通运输与物流学院，610031成都)

最小费用流问题是网络与流的核心问题之一，最基本的算法是Ford-Fulkerson算法，其他的算法还有网络单纯形算法(graph simplex algorithm)、松弛算法(relaxation algorithm)、消圈算法(cycle-canceling algorithm)、瑕疵算法(out-ofkilter algorithm)等等［1-8］，这些算法都可以解决单一品种流的最小费用流分配问题.在实际的交通网络应用中，普遍出现了多品种流问题，所以有了流变换、流分解、组合应用、多品种流及预流推进等新的理论和方法［9-13］，但这些算法都没有彻底解决多品种流的最小费用流分配问题.针对交通运输领域出现的多品种流交通网络，有必要对其最小费用流分配问题作进一步研究，并在其他算法的基础上，构造可行的最小费用流分配算法.

本文主要对运送费用无差异的多品种流交通网络相关问题进行分析，再基于连续最短路算法(successive shortestpath algorithm)和 Ford-Fulkerson算法的思路，构造相应的多品种流交通网络的最小费用流算法.

1 运送费用无差异的多品种流交通网络分析

1.1 运送费用无差异的多品种流的交通网络引例

为了解运送费用无差异的多品种流交通网络最小费用流问题，也为清晰地阐述相关算法的研究，先给出运送费用无差异的多品种流交通网络的一个引例.

引例 有一交通网络如图1所示，图中的边分别给出了运送能力和运送量，即边的容量、流量(零流)、费用.其中x1有Ⅰ、Ⅱ两种产品，质量分别为18、8 t;x2有Ⅱ、Ⅲ两种产品，质量分别为6、19 t．y1、y2、y3为3 个需求地，y1需要Ⅰ、Ⅱ 两种产品，需求量分别为6、7 t;y2需要Ⅱ、Ⅲ两种产品，需求量分别为4、9 t;y3需要Ⅰ、Ⅲ两种产品，需求量分别为8、13 t．现在需要设计的方案是在满足总运送费用最少的前提下，将尽可能多的产品运送到需求地．

图1 多品种流交通网络图

针对此引例，再利用传统的最小费用流算法，就不能设计出可行的最小费用流分配方案，所以有必要研究此类多品种流交通网络的最小费用流问题.

1.2 运送费用无差异的多品种流交通网络问题分析

先给定单一品种流的交通网络G=(V，E，C，F，W，X，Y)，其中顶点集合 V=(v1，v2，…，vn)，边E=(e1，e2，…，em)．对集合V取定两个非空子集X和Y，X为只发出流量的顶点集合，Y为只接收流量的顶点集合，且X∩Y=Ø，把X中的顶点x称为网络G的源，Y中的顶点y称为网络G的汇．针对边(vi，vj)赋予 3 个非负的整数参数cij、fij、wij，分别为容量、流量、费用．设顶点vi∉X、Y，即vi为转运点，用f+(vi)表示顶点vi发出的流量之和，f-(vi)表示顶点vi接收的流量之和．设分配目标流的流值为A，fA为流值为A的网络流，即Valf=A．

以上给出的交通网络描述，是针对运送费用无差异的单一品种流，在实际的交通网络中，在同一个阶段不同品种流运送费用相同的多品种流现象普遍存在，下面对运送费用无差异的多品种流交通网络特点进行分析.

设r为q个多品种中的第r个品种，其中r=1，2，…，q．fijr为第r个品种在边(vi，vj)上的流量，f+(vir)表示顶点vi发出第r个品种的流量之和，f-(vir)表示顶点vir接收第r个品种的流量之和．wij为所有品种在边(vi，vj)上的运送费用．边(vi，vj)也要遵从容量约束条件，即所有品种的流量之和要小于该边的容量，则有所有转运顶点vi也都要遵从流量守恒条件，而这里所谓的流量守恒是，既要保证所有品种的流量总和守恒，也要保证每一个单一品种的分量之和守恒，则有

基于以上分析，运送费用无差异的多品种流交通网络最小费用流分配的线性规划模型如模型(1)所示.针对模型(1)所刻画的多品种流交通网络，需要设计特定的最小费用流分配算法.

2 运送费用无差异的多品种流交通网络最小费用流算法设计

单一品种流最小费用流Ford-Fulkerson算法，是通过构造增流网络，在增流网络中寻找关于费用代数和最低的路径，再针对此路径所对应原网络中的增流链进行流量调整.

针对运送费用无差异的多品种流交通网络，再构造增流网络，势必会造成增流网络的结构变得庞大而且复杂，同时计算过程更为繁琐，所以直接利用Ford-Fulkerson算法可行但不是优化的方法.

2.1 算法思想

本文在借鉴连续最短路算法和Ford-Fulkerson算法的基础上，将网络图中边的属性设计为复合参数的形式，再针对流量分配构建复合指标，从而建立运送费用无差异的多品种流交通网络最小费用流算法.

2.1.1 复合参数及复合指标的设定

复合参数．费用没有差异的单一品种流交通网络中，边(vi，vj)的属性参数为(cij，fij，wij)．针对运送费用无差异的多品种流，本文把边(vi，vj)的属性设计为复合参数形式，即为［cij，fij(fij1，…，fijr，…，fijq)，wij］，其中fij(fij1，…，fijr，…，fijq)表示边(vi，vj)的总流量fij中，每个品种的分流量的多少．

复合指标．在连续最短路算法中，顶点vj的指标为(l(vj)，vi)，其中l(vj)表示从起点经过顶点vi到顶点vj关于费用的最短路长度，vi表示vj的前一个顶点．在Ford-Fulkerson算法中，针对流量调整，顶点vj的指标为(u，边的方向，δ)，其中u表示被标识点vj的前一个顶点;边的方向通过“+”或“-”来标识是前向边还是后向边;δ表示流量的调整量．针对多品种流交通网络，既要考虑最短路指标和流量调整指标，还要考虑多品种问题，所以本文构建了复合指标，其形式为(l(vj)，vi，边的方向)|［λ(λ1，…，λr…，λp)］．其中l(vj)表示第r个品种从起点经过前一个顶点vi到顶点vj，关于运送费用最低的最短路长度;vi表示顶点vj的前一个顶点;边的方向表明边(vi，vj)是前向边还是后向边，即(vi，vj)的流量是增加还是减少;λ表示在关于运送费用最低的当前链路中，针对总流量fij的调整量;λr表示在当前链路中，针对第r个品种分流量fijr的最大可能调整量．

2.1.2 复合指标中相关指标的计算规则

规则1 若边(vi，vj)为前向边且fij＜cij时，l(vj)=min{l(vj)，l(vi)+Wij}，λ=min{λ，cijfij}．因为此时总流量只能增加，而每个品种的分流量都有增加的可能性，所以λr=λ，其中r=1，2，…，q．

规则2 若边(vi，vj)为后向边且fij＞0，l(vj)=min{l(vj)，l(vi)-Wij}，λ=min{λ，fij}．因为此时总流量只能减小，每个品种的分流量都有减小的可能性，但每个品种的分流量不能减小为小于0，所以λr=min{λ，fijr}，其中r=1，2，…，q．

规则1、2基于连续最短路算法给出了当前最短路的长度l(vj);基于Ford-Fulkerson算法给出了当前链路中针对总流量fij的调整量λ;基于前面的容量约束条件，给出了当前链路中针对第r个品种分流量fijr的最大可能调整量λr．

2.1.3 增流链的流量调整量确定规则

尽管规则1、规则2计算了当前链路的相关指标，但针对第r个品种的分流量fijr，只给出了最大可能的调整量，那么针对从源到汇的增流链，总流量fij的调整量以及各个品种分量fijr的调整量还没有最终确定．

设针对增流链总流量fij的调整量为δ，基于Ford-Fulkerson算法可知δ=min{λ，A-Valf}．

设针对增流链品种分量fijr的调整量为δr，下面给出确定δr的规则3和规则4．

规则3 若至少存在一个品种的最大可能调整量与总流量调整量相等，即有 max{λ1，…，λr…，λp}=δ，则任取其中一个最大的关于品种k的λk，令δk=λk=δ，此时增流链的总流量以及分流量的调整量即为 δ(0，…，δk，…，0)．

规则4 若不存在任意一个品种的最大可能调整量与总流量调整量相等，即 max{λ1，…，λr…，λp}＜δ，则任取其中一个最大的λk，令δk=λk．此时针对分流量的调整幅度还剩余δ=δδk，再任取其余一个最大的 λm，即 λm=max{λ1，…，λr…，λp;其中不包含 λk}，那么 δm=min{δ，λm}．此时针对分流量还剩余δ=δ-δm，依次如上类推，直到δ=0为止．没有被确认的分流量的调整量λi=0．此时增流链的总流量以及分流量的调整量即为 δ(0，…，δk，…，δm，…，0)．

规则3、规则4是在所有品种流量之和要小于该边容量的基础上，对分流量调整幅度最大的品种来优先增加流量，目的是在运送费用最低的增流链上，尽可能多的增加分流量.

2.1.4 增流链的流量调整规则

基于Ford-Fulkerson算法，将关于运送费用最低的增流链的流量进行调整，即增流链中的边(vi，vj)的复合参数按照如下规则修改．

规则5 若(vi，vj)为前向边，其复合参数修改为［cij，fij+δ(fij1+δ1，…，fijr+δr，…，fijq+δq)，wij］;若(vi，vj)为后向边，其复合参数修改为［cij，fij-δ(fij1-δ1，…，fijr-δr，…，fijq-δq)，wij］．

2.2 算法步骤

基于给出的复合参数、复合指标以及相应的规则，本文算法的思路是，随着所求最短路的延伸，同时消除非增流边，这样既杜绝了二次求解问题，也避免了全枚举的问题，算法步骤如下.第1～3步为初始化过程，第4～8步为寻找费用最低的增流链过程，第9～11步为流量调整过程.

第1 步 设源 X={x1，…，xi，…，xn}，转运点 V={v1，…，vi，…，vn}，汇 yi={y1，…，yi，…，yn}．设源xi具有第r品种的数量为sir，汇yi需要第r品种的数量为．设λ=λr=+∞，设集合S=Ø，集合 T={x1，…，xi，…，xn，v1，…，vi，…，vn，y1，…，yi，…，yn}．

第2步 对运送费用无差异的多品种流交通网络，在零流(平凡流)基础上，利用给出的容量、费用，把边的属性设为复合参数形式，即［cij，fij(fij1，…，fijr，…，fijq)，wij］， 此 时 初 始 的 流 量fij(fij1，…，fijr，…，fijq)均为 0(0，…，0，…，0)，即有Valf=0．

第3步 设l(xi)=0，对起点xi赋予复合指标(0，0，+)|［+∞(+∞，…，+∞…，+∞)］;设其余顶点的l(vi)=+∞、l(yi)=+∞，那么其余顶点均可以赋予复合指标(+∞，0，+)|［+∞(+∞，…，+∞，…，+∞)］．

第4步 选择起点xi检查，将起点xi复合指标标上*，表示顶点vi已被检查．同时设集合S={xi}，xi∉ T．

第5步 若xi与其他顶点没有直接连线，其他顶点的复合指标保持不变;若有直接连线，则计算其他顶点的复合指标值，计算方法如下:1)(xi，vj)为前向边．若fij=cij，此时流量不能增加，即边(xi，vj)不能成为增流链中的边，那么最短路也就不能经过该边，此时顶点vj的复合指标保持不变．若fij＜cij，此时流量可以增加，即边(xi，vj)可以成为增流链中的边，那么最短路也就可以经过该边．复合指标中的各个指标计算如下:按照规则1可知l(vj)=min{l(vj)，l(xi)+Wij}，如果l(vj)值来自第1项l(vj)，顶点vj的复合指标保持不变．如果l(vj)值来自第2项l(xi)+Wij，总流量调整量λ=min{λ，cij-fij，A-Valf}．当vj∈V时，所有品种的最大可能调整量λr=λ．当vj∈Y时，若-f+(xik)=0或-f-(yjk)=0，则k品种的最大可能调整量λk=0，其余品种的最大可能调整量λr=min{λ，tjk-f-(yjk)};否则，所有品种的最大可能调整量λr=min{λ，tjk-f-(yjk)}．此时需要将顶点vj复合指标修改为(l(vj)，xi，边的方向)|［λ(λ1，…，λr…，λp)］．2)(xi，vj)为后向边．若fij=0，此时流量不能减少，即边(xi，vj)不能成为增流链中的边，那么最短路也就不能经过该边，此时顶点vj的复合指标保持不变．若fij＞0，此时流量可以减少，即边(xi，vj)可以成为增流链中的边，那么最短路也就可以经过该边．复合指标中的各个指标计算如下:按照规则2可知l(vj)=min{l(vj)，l(xi)-Wij}，如果l(vj)值来自第1项l(vj)，顶点vj复合指标保持不变．如果l(vj)值来自第2项l(xi)-Wij，总流量的调整量 λ=min{λ，fij，A-Valf}．当vj∈ V 时，所有品种的最大可能调整量λr=min{λ，fijr}．当vj∈Y时，若-f+(xik)=0或-f-(yjk)=0，则k品种的最大可能调整量λk=0，其余品种的最大可能调整量λr=min{λ，fijr，tjk-f-(yjk)};否则，所有品种的 最 大 可 能 调 整 量 λr=min{λ，fijr，tjk-f-(yjk)}．此时需要将顶点vj复合指标修改为(l(vj)，xi，边的方向)|［λ(λ1，…，λr…，λp)］．

第6步 针对顶点vj，计算l(vj)*=min{l(vj);其中j=1，2，…，n;vj∉ S}．将顶点vj的复合指标标上*，表示顶点vj已被检查，设集合S={xi，…，vj}，vj∉T．当vj∈Y时，转第9 步，否则转第7步．

第7步 从顶点vj出发，求其他顶点vk的复合指标．若顶点vj与顶点vk没有直接连线，顶点vk的复合指标保持不变;若有直接连线，则计算顶点vk的复合指标值，计算方法如下:1)(vj，vk)为前向边．若fjk=cjk，此时流量不能增加，即边(vj，vk)不能成为增流链中的边，那么最短路也就不能经过该边，此时顶点vk的复合指标保持不变．若fjk＜cjk，此时流量可以增加，即边(vj，vk)可以成为增流链中的边，那么最短路也就可以经过该边．复合指标中的各个指标计算如下:按照规则1可知l(vk)=min{l(vk)，l(vj)+Wjk}，如果l(vk)值来自第1项l(vk)，顶点vk的复合指标保持不变．如果l(vk)值来自第2项l(vj)+Wjk，总流量的调整量λ=min{λ，cjk-fjk，A-Valf}．当vk∈ V 时，所有品种的最大可能调整量λr=λ．当vk∈Y时，若-f-(yjk)=0，则k品种的最大可能调整量λk=0，其余品种的最大可能调整量-f-(yjk)};否则，所有品种的最大可能调整量λr=min{λ，tjk-f-(yjk)}．此时需要将顶点vk复合指标修改为(l(vk)，vj，边的方向)|［λ(λ1，…，λr，…，λp)］．2)(vj，vk)为后向边．若fjk=0，此时流量不能减少，即边(vj，vk)不能成为增流链中的边，那么最短路也就不能经过该边，此时顶点vk的复合指标保持不变．若fjk＞0，此时流量可以减少，即边(vj，vk)可以成为增流链中的边，那么最短路也就可以经过该边．复合指标中的各个指标计算如下:按照规则2可知l(vk)=min{l(vk)，l(vj)-Wjk}，如果l(vk)值来自第1项l(vk)，顶点vk复合指标保持不变．如果l(vk)值来自第2项l(vj)-Wjk，总流量的调整量 λ=min{λ，fjk，AValf}．当vk∈V时，所有品种的最大可能调整量λr=min{λ，fjkr}．当vk∈Y时，若tjk-f-(yjk)=0，则k品种的最大可能调整量λk=0，其余品种的最 大 可 能 调 整 量 λr=min{λ，fjkr，tjk-f-(yjk)};否则，所有品种的最大可能调整量λr=min{λ，fjkr，tjk-f-(yjk)}．此时需要将顶点vk复合指标修改为(l(vk)，vj，边的方向)|［λ(λ1，…，λr…，λp)］．

第8步 针对顶点vk，计算l(vk)*=min{l(vk);其中j=1，2，…，n;vk∉ S}．将顶点vk复合指标标上*，表示顶点vk已被检查，设集合S={xi，…，vk}，vk∉ T．当vk∈ Y 时，转第9 步．

第9步 当yi⊆S时，自汇yi逆向追踪，沿着每个顶点复合指标中第1个子指标组的vi即可得出运送费用最低的增流链，路长为l(yi)，总流量的调整量δ=λ．再按照规则3、4，即可确定出增流链中每个品种的分流量的调整量δr．

第10步 按照规则5，对增流量的总流量及分流量进行调整.

第11步 转到第3步，反复进行，直到找不到关于运送费用最低的增流链为止.

3 示例求解

为了说明本文算法，下面对引例进行最小费用最大流分配，最小费用最大流的目标流是最大流，此时将算法中总流量调整量λ公式中的AValf去掉即可.由于图显示空间的局限，不对顶点进行复合指标的标号;另外，因篇幅限制，将相应的计算过程省略.

第1步 设集合S=Ø，集合T={x1，x2，v1，v2，v3，y1，y2，y3}．此时初始的流量fij(fij1，fij2，fij3)均为 0(0，0，0)．此问题涉及 I、II、III 3 个品种，这里用1、2、3序号来标识．对起点xi均赋予复合指标(0，0，+)|［+∞(+∞，+∞，+∞)］;对其余各个顶点均可以赋予复合指标(+∞，0，+)|［+∞(+∞，+∞，+∞)］．图2为求解时流量调整以后某一过程的状态图．

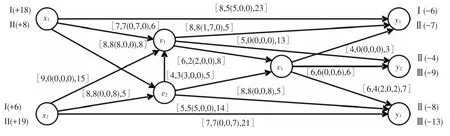
图2 某一过程流量调整后的状态图

第2步 对图2继续寻找关于运送费用最低的增流链．表1为分别从源x1、x2出发的复合指标计算结果表(此计算过程省略)．

表1 复合指标结果

针对表1取l(vj)*=min{l(vj);vj∉S}=min{15，23}=15=l(v1)* ，将表1中顶点v1的指标标记* ，此时 S={x1，x2，v1}，集合T={v2，v3，y1，y2，y3}．从顶点v1出发，继续求复合指标，顶点v1与顶点v2、v3、y1、y2有直接连线，只需计算这4个顶点的复合指标即可，其余顶点复合参数保持不变，详细计算过程如下:1)(v1，v2)为后向边，同时f12=3＞0，此边可以成为增流链中的边，则l(v2)=min{l(v2)，l(v1)-W12}=min{+∞，10}=10，l(v2)值来自第2项，总流量的调整量λ=min{λ，f12}=min{9，3}=3，v2∈V，各个品种的最大调整量分别为λ1=3，λ2=λ3=0．2)(v1，v3)为前向边，同时f13=2＜c13=6，此边可以成为增流链中的边，则l(v3)=min{l(v3)，l(v1)+W13}=min{+∞，23}=23，l(v2)值来自第2项，总流量的调整量 λ=min{λ，c13-f13}=min{9，6-2}=4，此时v3∈V，各个品种的最大调整量分别为λ1=λ2=λ3=4．3)(v1，y1)为前向边，此时f11=8=c11=8，此时总流量不能增加，即边不可以成为增流链中的边，那么最短路也就不能经过该边，此时顶点y1的复合指标保持不变．4)(v1，y2)为前向边，同时f12=0＜c12=5，此边可以成为增流链中的边，则l(y2)=min{l(y2)，l(v1)+W12}=min{+∞，28}=28，l(y2)值来自第2项，总流量的调整量λ=min{λ，c12-f12}=min{9，5-0}=5．汇y2不需要第I品种，则第I品种的最大可能调整量λ1=0;针对第II品种有λ2=min{λ，t22-f-(y22)}=min{5，4-0}=4;对第Ⅲ品种有λ3=min{λ，t23-f-(y23)}=min{5，9-6}=3．修改后的复合指标如表2所示．

表2 复合指标结果

针对表2取l(vj)*=min{l(vj);vj∉S}=min{10，23，23，28}=10=l(v2)* ，将表 2 中顶点v2的指标标记 *．此时 S={x1，x2，v1，v2}，集合 T={v3，y1，y2，y3}．从顶点v2出发，继续求复合指标，顶点v2与顶点v3、y3有直接连线．但由于在前向边(v2，v3)上，f23=8=c23=8，此时流量不能增加，即边(v2，v3)不能成为增流链中的边，那么最短路也就不能经过该边，此时顶点v3的复合指标保持不变;同理，在前向边(v2，y3)上由于f23=5=c23=5，流量不能增加，此时顶点y3的复合指标保持不变．此种情况说明，无法通过顶点v2找到一条到达汇的增流链，此时需要返回到前一个顶点v1，通过与顶点v1有直接连线的其他顶点来寻找最短路．针对表2取l(vj)*=min{l(vj);vj∉ S}=min{23，23，28}=23=l(y1)=l(v3)*，这里选择顶点v3作为标记点，即将表2中顶点v3的指标标记 *．此时 S={x1，x2，v1，v2，v3}，集合 T={y1，y2，y3}．

从顶点v3出发，继续求复合指标，顶点v3与顶点y1、y2、y3有直接连线，只需要计算这3个顶点的复合指标即可，其余顶点复合参数保持不变，详细计算过程如下:1)(v3，y1)为前向边，此时f31=0＜c31=4，此边可以成为增流链中的边，则l(y1)=min{l(y1)，l(v3)+W31}=min{23，26}=23，l(y1)值来自第1项，顶点y1的复合指标保持不变．2)(v3，y2)为前向边，此时f32=c32=6，此时流量不能增加，即边(v3，y2)不能成为增流链中的边，那么最短路也就不能经过该边，顶点y2的复合指标保持不变．3)(v3，y3)为前向边，此时f33=4＜c33=6，此边可以成为增流链中的边．则l(y3)=min{l(y3)，l(v3)+W33}=min{+∞，30}=30，l(y3)值来自第2项，总流量的调整量λ=min{λ，c33-f33}=min{4，6-4}=2，此时针对第I品种有=8-(5+2)=1，则第I品种的最大可能调整量 λ1=minf-(y31)}=min{2，1}=1;针对第Ⅱ品种有-f-(y32)=0，则第Ⅱ品种的最大可能调整量λ2=0;针对第Ⅲ品种有=13-(0+2+7)=4，则第Ⅲ品种的最大可能调整量λ3=min{λ，t33-f-(y33)}=min{2，4}=2．修改后的复合指标如表3所示．

表3 复合指标结果

针对表3取l(vj)*=min{l(vj);vj∉S}=min{23，28，30}=23=l(y1)*．由此可知关于费用的最短路的增流链应为x1→y1，但由于汇y1需要的第I、II品种已全部满足，其流量无法增加，此时需要选择包含汇的次最短路．针对表3取l(vj)*=min{l(vj);vj∉S}=min{28，30}=28=l(y2)*．将表3中顶点y2的指标标记*，此时S={x1，x2，v1，v2，v3，y2}，集合T={y1，y3}．因为y2⊆S，说明已经找到关于运送费用最低的增流链．

自汇y2，沿着每个顶点复合指标中第1个子指标组的第2个指标逆向追踪，可得出关于费用的最短路为x2→v1→y2，路长为28，总流量调整量 δ=5．因为 max{λ1，λ2，λ3}=max{0，4，3}≤δ=5，则任取其中一个最大的λ2=4，令δ2=λ2=4．此时针对分流量的调整幅度还剩余δ=δ-δ2=5-4=1，再任取其余一个最大的λ3，则δ3=min{δ，λ3}=min{1，3}=1，此时分流量的调整幅度已经为δ=0，则δ1=0．即增流链的总流量及分流量的调整量为5(0，4，1)．流量分配结果如图3所示．

第3步 针对图3继续寻找关于运送费用最低的增流链，余下过程省略，最终的最小费用最大流分配结果如图4所示.

针对图4，仍能寻找到增流链x2→v1→v3→y1，但由于y1所需要的第I、II品种已经全部得到满足，不需要对流量进行增加，并且从源x1、x2出发的边中，只有边(x1，y1)为不饱和边，但汇y1需要的第I、II品种已经得到全部满足，不需要对流量进行增加，因此此时为最小费用流．由图4可以知道，该引例中各个品种的具体运送方案，把该引例的总体方案以及各个品种的具体方案汇总，发送和接收的总量均为42，则3个品种的费用WⅠ、WⅡ、WⅢ分别为299、189、365，总费用W=WⅠ+WⅡ+WⅢ=853．

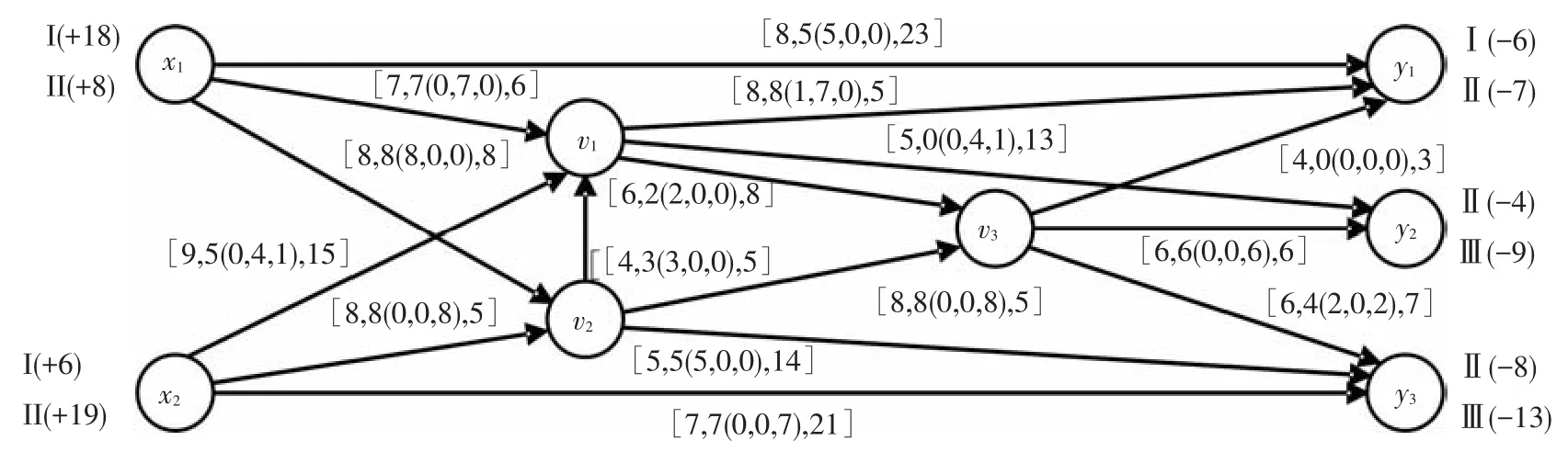
图3 流量调整后的状态图

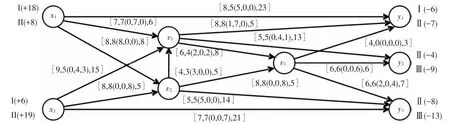
图4 多品种流的最小费用最大流量终分布状态图

4 结论

1)在连续最短路算法和Ford-Fulkerson算法基础上，通过构建复合指标，建立了运送费用无差异的多品种流最小费用流分配方法，另外，通过设计复合参数，也标定了多品种流的流量分配状态.

2)构造的基于复合参数和复合指标的多品种流最小费用流算法，避免了传统算法需要改变网络图结构的不足，在算法实现上也体现了便利.在交通运输领域，存在运送费无差异的多品种流分配问题，但针对此类问题的研究文献还不多见，该算法也为解决交通网络的一系列相关实际问题提供了应用基础.

3)在实际应用中，多品种流大部分会存在费用上的差异，相对的算法设计难度较大，在此研究的基础上，后期需要研究运送费用有差异的多品种流交通网络最小费用流分配问题.

［1］寇玮华.运筹学［M］.成都:西南交通大学出版社，2013.

［2］甘爱英.运筹学［M］.北京:清华大学出版社，2002.

［3］寇玮华，崔皓莹.满足交通网络流量增长态势的扩能优化研究［J］.交通运输工程与信息学报，2012，10(4):19-25.

［4］寇玮华，董雪，吕林剑.交通运输网络中两个结点间有流量约束的最小费用最大流算法［J］.兰州交通大学学报，2009，28(6):104-109.

［5］谢政，汤泽滢.带模糊约束的最小费用流问题［J］.模糊系统与数学，1999，13(2):90-941.

［6］程琳，王炜.Dial交通量分配模型和选择率问题的研究［J］.交通运输系统工程与信息，2002，2(3):29-32.

［7］陈光亚.带有向量值费用函数的交通网络平衡问题:模型与分析［J］.交通运输系统工程与信息，2006，6(5):56-58.

［8］任刚，王炜.可直接计算转向流量的改进型Dial交通分配算法［J］.中国公路学报，2005，18(4):83-86.

［9］ORLIN J B.Network optimization［EB/OL］.［2010-05-08］.http://www.core.org.cn/OcwWeb/index.htm.

［10］CHABINI I，ODONI A R.Transportation flow system［EB/OL］.［2012-03-16］.http://www.core.org.cn/OcwWeb/index.htm.

［11］SHEPHERD B，ZHANG L.A cycle augmentation algorithm for minimum cost multicommodity flows on a ring ［J］. Global Tele communications Conference，1999，2:1535-1543.

［12］RETVARI G，BIRO J J，CINKLER T.A novel lagrangian-relaxation to the minimum cost multicommodity flow problem and its application to OSPF traffic engineering ［J］. Computers and Communications，2004，2:957-962.

［13］寇玮华，崔皓莹.有运送路径限制的多品种流交通网络最小费用流算法研究［J］.兰州理工大学学报，2013，32(6):1-7.