基于自由振荡理论的有压管道堵塞检测方法

伍悦滨，徐 莹，汪 芬

基于自由振荡理论的有压管道堵塞检测方法

伍悦滨1，2，徐 莹3，汪 芬4

（1.哈尔滨工业大学城市水资源与水环境国家重点实验室，150090哈尔滨；2.哈尔滨工业大学市政环境工程学院，150090哈尔滨；3.哈尔滨商业大学能源与建筑工程学院，150028哈尔滨；4.广东省电力设计研究院，510660广州）

为了解决有压管道的堵塞问题，根据自由振荡理论的基本原理，提出适于检测管道堵塞的数值模拟简化模型，得出了确定管道堵塞的定位与定量的方法.基于有压瞬变流理论，结合振动理论，引入迪拉克函数，建立包含堵塞的管道瞬变流控制方程；对方程进行无量纲化并线性化，使其得到简化.在固定边界条件下，求出相对压力的解析解，对其进行傅立叶级数分析，得到各谐波在各相对周期中的振幅，由此可计算出各谐波的衰减指数.求解结果表明：堵塞衰减与管道流量成正比，管道堵塞的相对位置与堵塞衰减参数呈余弦关系，只要已知两个谐波的堵塞衰减参数即可确定堵塞位置和堵塞量级.

管道堵塞；瞬变流；自由振荡；堵塞衰减；阻尼衰减

堵塞是有压管道系统中普遍存在的问题，根据相关资料统计发现引起管道堵塞的原因［1］主要有以下几点：在设计阶段，管道设计的不合理；在实际运行阶段，管道内流速达不到设计要求，有沉淀物淤积；施工中设计阀门质量差，致使阀门失灵，阀门螺杆损坏、折断等；人为破坏造成管道的堵塞等.堵塞会对有压管道造成许多严重后果，例如，在给水管道中，堵塞会破坏给水管道正常的工作状态，降低给水系统的工作效率，更甚者会破坏供水的水质，给城市居民的健康带来危害.另外，给水管道中的堵塞会引起管道内压力的上升，从而导致管道的应力破坏，致使泄漏甚至爆管，出现生产事故，导致宝贵的水资源浪费.如果出现大面积的流失，就不仅仅是资源的浪费，而且引起环境的污染，甚至发生水灾，严重威胁人民生命财产的安全［2-3］.因此对堵塞进行检测和控制是很有必要的.

在检测和控制管道堵塞的方法中，质量守恒的方法已无法适用，因为堵塞的发生不能改变管道内流体在稳定状态下的质量守恒.然而，堵塞却会影响流体的动量守恒，这种动量的不守恒一般可以用流过堵塞时的水头损失表示出来，所以，堵塞的量可以通过压力的测量估计得到［4］.又由于堵塞本身可以引起管道的瞬变流，因此本文从有压管道瞬变流角度研究堵塞，应用流体自由振荡理论，分析管道系统中的流体的振荡来检测有压管道的堵塞.

1 单管堵塞模型及控制方程

自由振荡［5-6］是某些初始的、暂时的激励引起的.当消除该激励时，系统中的固有阻尼使振荡随时间发生衰减.按线性化讨论时，将产生指数衰减.当管道中发生堵塞时，受激瞬变流的衰减将会发生变化.为了提取在瞬变流状态下管道的堵塞信息，利用傅立叶级数，通过比较有无堵塞情况下受激瞬变流压力波的衰减速率，确定管道内的堵塞位置及堵塞量级.

单管系统的堵塞模型采用水箱-管道-水箱系统［7］，如图1所示.在瞬变分析过程中假设管道首末端水箱水位恒定不变.

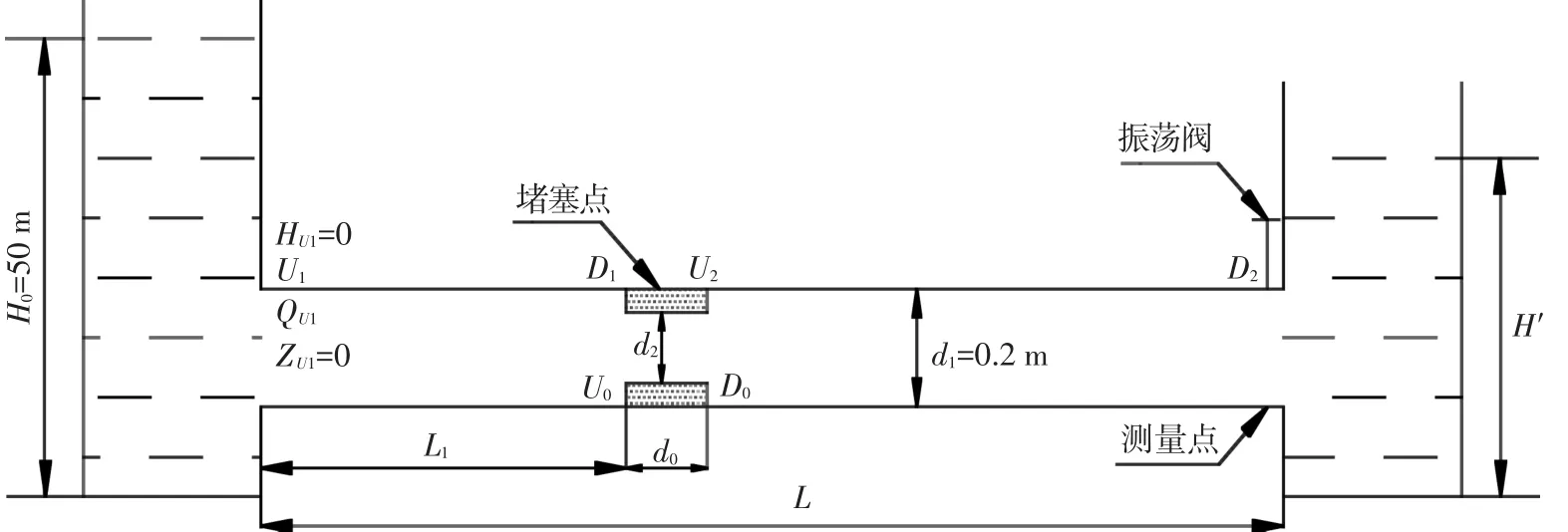
图1 单管堵塞

取微小控制体1-2，如图2所示.在管道内，靠近堵塞部分的水的流动可视为孔口出流.由控制体在x轴方向动量守恒，可得

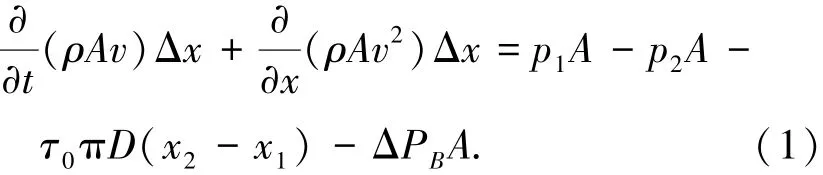
其中：p1为1断面处压强，N／m2；p2为2断面处压强，N／m2；τ0为管壁摩阻应力，N／m2；D为管径，m；A为管道的断面面积，m2；ρ为液体密度，kg／m3；v为管内流速，m／s；g为重力加速度，m／s2；x为位置坐标，m；ΔPB为水流经堵塞前后的压强变化量，N／m2.

令Δx趋于无穷小，可得

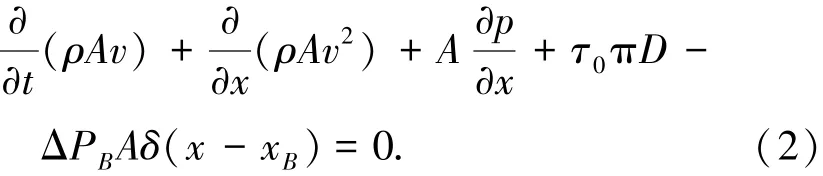
定义

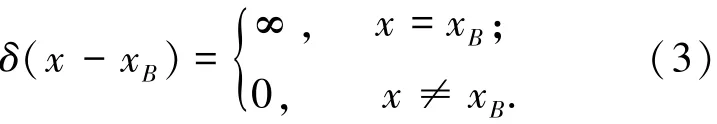
其中：δ（x-xB）为迪拉克函数，ε为距堵塞点很短的距离.

图2 有堵塞管道的控制体

考虑水的可压缩性及管壁的弹性，并作相应的简化，可以得到管道中有堵塞现象时的运动方程为

其中：H为任意点处的测压管水头，mH2O；Q为管道流量，m3／s；f为管道沿程阻力系数；ΔHB为水流经堵塞前后的测压管水头变化量，mH2O.

同理，当管道中有堵塞现象时的连续性方程为

其中：a为管道内水击波的传播速度，m／s.

由堵塞引起的水头损失［8］可表示为

其中：KB为堵塞的局部水头损失系数；KB随堵塞面积的不同而不同.

2 边界条件设定及解析解

将H和Q表示成平均值与脉动值之和分别为

同时将控制方程中各物理量化为无量纲物理量［9］，即

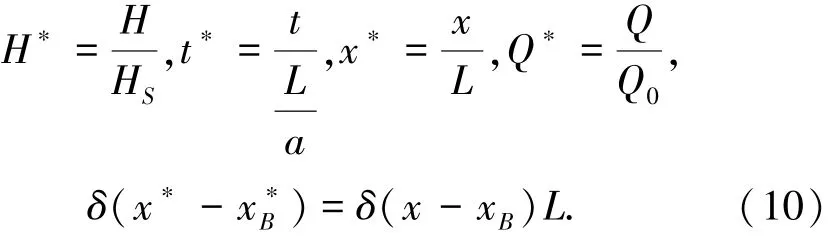
式中：H0为管道平均压力，mH2O；HS为儒柯夫斯基压力增量，；L为管道长度，m； Q0为管道平均流量，m3／s.简化式（5）、（6）后，得

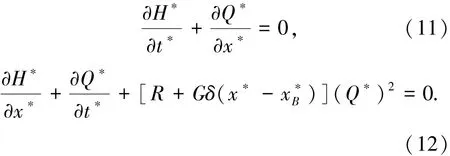
将H∗和Q∗表示成一个平均值与一个振荡值之和分别为

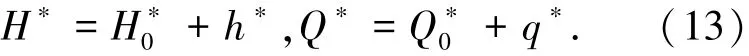
式中：h∗为相对振荡压力水头；q∗为相对振荡流量.

对方程（11）、（12）进行简化，可得

若已知边界条件为h∗（0，t∗）＝0、h∗（1，t∗）＝0，初始条件为gh（x∗），则无量纲方程的解［10-12］为

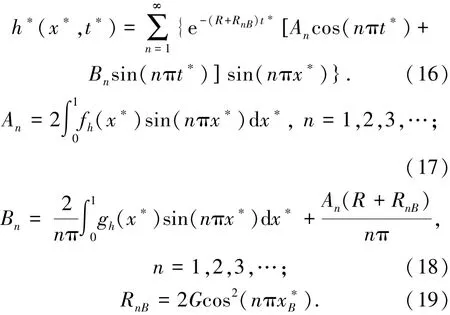
式中：RnB为n次谐波的堵塞衰减参数，为管道堵塞的相对位置.

由式（16）可知：1）有堵塞的管道压力脉动是一系列谐波成分之和，每一谐波都是以R＋RnB为指数呈指数衰减.2）R是阻尼衰减参数，与n无关，所有谐波成分的阻尼衰减都是以R为指数呈指数衰减的，并且相同.3）与阻尼衰减参数R不同的是，堵塞衰减参数RnB与n有关，尽管各谐波的堵塞衰减都是指数型衰减，但值各不相同的.

3 解析解的傅立叶级数展开及分析

当激励作用于系统后，在管道的某点测量其瞬变压力，分析得到相对脉动压力曲线，并将相对脉动压力曲线按周期分解，如图3所示，每一个瞬变周期都可以表示成傅立叶级数的形式.经分析，可得n次谐波的第i个周期的振幅［13］为

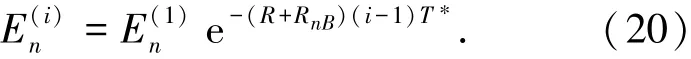
式中：E（1）n为第1个周期n次谐波的振幅.

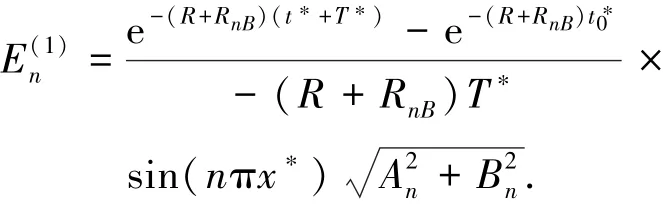
图3 相对脉动压力随时间的变化曲线

4 堵塞检测及算例分析

若测得的瞬变满足下列条件，则说明管道中存在堵塞：1）分解后各谐波的衰减指数R＋RnB明显不同；2）某些谐波的衰减指数明显大于阻尼衰减参数R.

4.1定位堵塞

对于每一谐波，堵塞引起的衰减都是堵塞位置和堵塞量级的函数，而两个堵塞衰减参数之比仅是堵塞位置的函数［12］，即

因此，堵塞的位置可以由两个堵塞衰减参数之比计算求得.阻尼衰减参数R可以在稳态条件下估算出f值后，计算求得.那么，任何一谐波的堵塞衰减参数RnB就等于该谐波的衰减指数（R＋RnB）减去阻尼衰减参数R.如图4所示，当堵塞位于管道不同点时，相应的二次谐波与一次谐波的堵塞衰减参数比值和三次谐波与一次谐波的堵塞衰减参数比值.

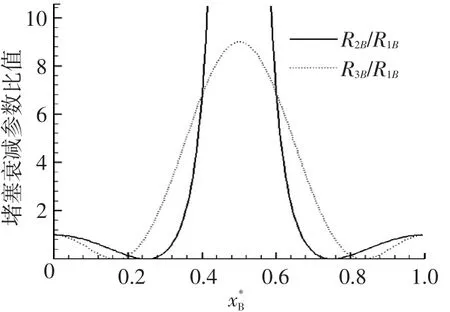
图4 两谐波成分的堵塞衰减参数比值

由于余弦函数的对称性，两个谐波成分的堵塞衰减参数之比与堵塞位置不是一一对应的关系.例如：除了堵塞点在管道中点，当堵塞点位于管道的其他点时，一个R2B／R1B值将求解出两个到4个堵塞位置的值.而高次谐波间的堵塞衰减参数之比，一个比值将求解出更多的可能堵塞位置的值.因此，在检测堵塞分析中仅用n＜4的谐波成分.

4.2定量堵塞

一旦确定了堵塞的位置，就可以由式（19）求出堵塞的量级［12］为

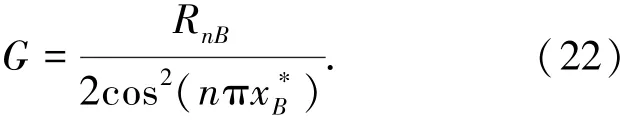
4.3算例分析

经过以上分析，检测管道堵塞的计算步骤归纳如下：1）当管道内水的运动状态趋于稳定时，监测管道末段压力的变化，是否小于计算值.若是，则管道中间某处可能产生堵塞以至局部阻力损失增大，末段压力值小于预期的计算压力值，执行下一步；若否，则判定为无堵塞，继续监测压力值.2）待管道中水的运动达到稳定状态后引发激励，产生监测堵塞的瞬变.3）测量管道某点或多点不同时间下的压力.4）将测得的压力值绘制成压力线，分析得到相对脉动压力曲线，并将相对脉动压力曲线按周期分解.5）利用傅立叶级数展开，将一个周期的瞬变分解成单独的谐波成分，并计算各谐波的振幅.6）沿着相对脉动压力曲线，将划分的各周期数据，重复步骤4.7）将每一周期的每一谐波的振幅用傅立叶级数表示成式（20）的形式.8）根据步骤6计算出E（1）n和R＋RnB.9）分析各谐波的衰减速率，检测堵塞的存在、堵塞位置及堵塞量级.

算例如图5［14］所示，无堵塞时管道内的平均流速为1.11 m／s，有堵塞时管道内的平均流速为1.07 m／s.待管道流体流动稳定后，通过调节下游水箱水面水位，产生激励：在0～1.6 s水箱水位从37.4 m上升到48 m，1.6～2.4 s水箱水位从48 m下降到37.4 m.

在管道1 500 m处测量瞬变流的压力值，将其连接成线，如图6所示.通过分析瞬变压力曲线，可以得到相对脉动压力随时间的变化曲线，如图7所示.

图5 有堵塞的管道

图6 瞬变压力随时间的变化曲线

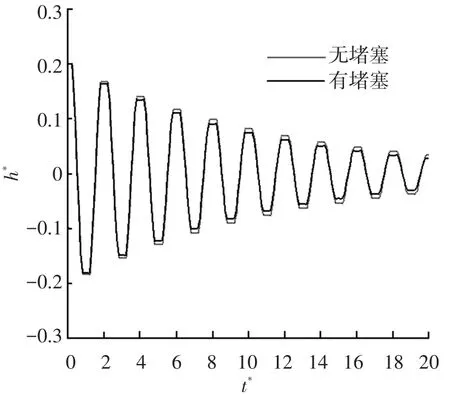
图7 相对脉动压力随时间的变化曲线

将相对脉动压力随时间的变化曲线按周期分解，并利用傅立叶级数分析.各谐波在不同周期时的振幅如图8所示.将图8中各点连接成线，即可得到各谐波的衰减曲线，如图9所示.

由已知条件可计算管道无堵塞时的阻尼衰减参数

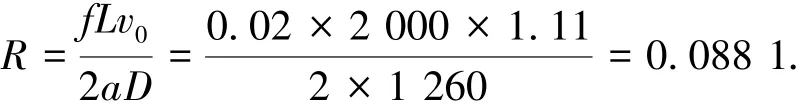
有堵塞时的阻尼衰减参数

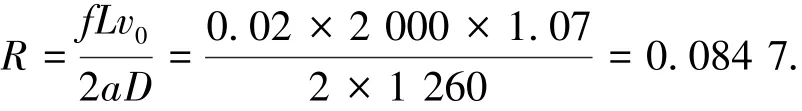
图9中，无堵塞时两条曲线的衰减速率R＋RnB相等，均为0.088 1，这就是管道阻尼衰减参数R，与计算值相等.图9中，有堵塞时两条曲线的衰减速率R＋RnB分别为0.094 4、0.086 3，均大于0.084 7.因此，两种谐波成分的堵塞衰减参数分别为根据图4，当0.798、＝0.126、＝0.874）.

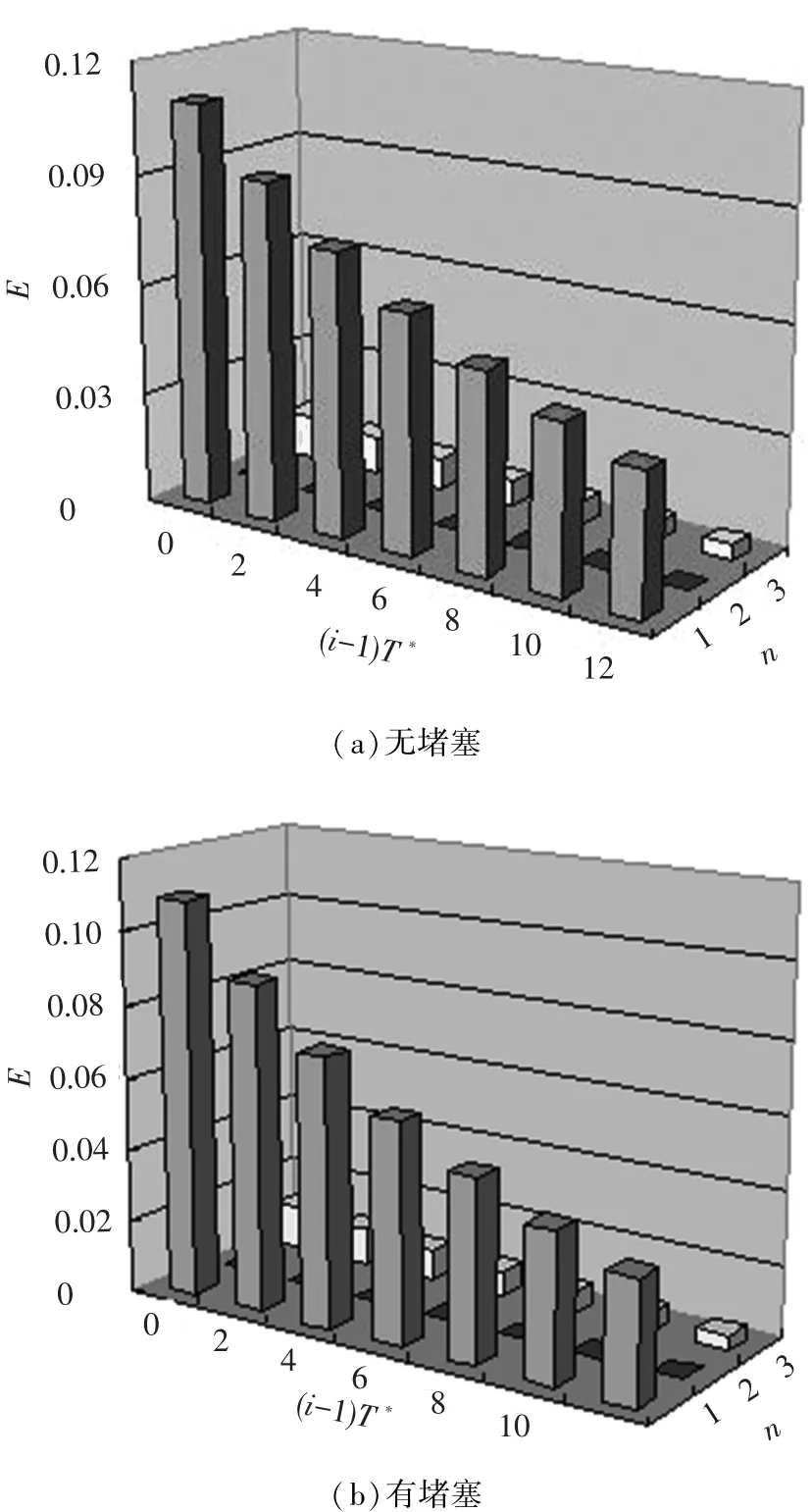
图8 各谐波在不同周期时的振幅

图9 不同谐波成分的指数衰减曲线

本方法无需特殊的管道原始资料，需要管道的管径、长度和水源处的压力值即可进行计算，另外还需要考虑到管道的承压能力，因为在管道中产生水击时，管壁应该能够承受水击产生的压力.本检测堵塞的方法是基于自由振荡模型及控制方程的，所以适用条件和范围与模型假设相同，即相同管径中水击波的传播速度相同；管道首末端水箱水位恒定不变.而且，对于堵塞程度没有要求，轻微堵塞与完全堵塞都可以进行检测.

5 结 论

1）对于有堵塞的管道，系统自由振荡的衰减由系统阻尼衰减和堵塞衰减组成.由两个谐波的堵塞衰减参数之比可以确定堵塞位置，堵塞量级可以由公式计算确定.

2）堵塞衰减与管道流量成正比，与管道压力没有直接关系.因此，在检测管道堵塞时，应使管道的流量在满足设计要求条件下适当增大以提高检测效果.

3）管道堵塞的相对位置与堵塞衰减参数呈余弦关系，只要已知两个谐波的堵塞衰减参数即可确定堵塞位置和堵塞量级.

4）基于自由振荡理论的有压管道堵塞检测技术不仅可以用于单管中的堵塞检测，也可以用于单管的漏失检测.

［1］邱正阳，邓松圣，蒋士章，等.管道探堵研究［J］.油气储运，2006，25（5）：33-35.

［2］胡国华.谈住宅给排水管道渗漏堵塞原因及防治方法［J］.建筑知识，1995（6）：19-20.

［3］敖东明，姜桂兰.给排水管道的渗漏、堵塞原因及预防措施［J］.内蒙古科技与经济，2001（1）：64-65.

［4］刘恩斌，李长俊，彭善碧，等.基于压力波法的管道堵塞检测技术［J］.天然气工业，2006，26（4）：112-114.

［5］WYLIE E B，STREETER V L.Fluid transients［M］.New York：McGraw⁃Hill Book Co，1993.

［6］刘天顺.瞬变流反问题分析在给水管网漏失检测中的应用［D］.哈尔滨：哈尔滨工业大学，2003.

［7］WYLIE E B，STREETER V L.Fluid transients in systems［M］.New Jersey：Prentice⁃Hall Inc，Englewood Cliffs，1993.

［8］MILLER D S.Internal flow systems［M］.Michigan：BHRA Fluid Engineering，1978.

［9］WYLIE E B.Unsteady internal flows⁃dimensionless numbers and time constants［C］／／7th International Conference on Pressure Surges＆Fluid Transients in Pipelines and Open Channels.Harrogate，UK：Dr Don J Wood’s Publications，1996：313-322.

［10］LEVINE H.Partial differential equations：American mathematical society［M］.New York：International Press，1997.

［11］KREYSZIG E.Advanced engineering mathematics［M］.New York：John Willy＆Sons，Inc，1999.

［12］WANG X J.Leakage and blockage detection in pipelines and pipe network systems using fluid transients［D］.Adelaide，Australia：University of Adelaide，2002.

［13］PRESS W H，TEUKOLSKY S A，VETTERLING W T，et al.Numerical recipes：the art of scientific computing［M］.Cambridge：Cambridge University Press，1992.

［14］汪芬.基于流体振荡理论的给水管道堵塞模拟研究［D］.哈尔滨：哈尔滨工业大学，2007.

（编辑魏希柱）

Blockage detection in water⁃supply pipelines based on auto⁃oscillation theory

WU Yuebin1，2，XU Ying3，WANG Fen4
（1.State Key Laboratory of Urban Water Resource and Environment，Harbin Institute of Technology，150090 Harbin，China；2.School of Municipal and Environmental Engineering，Harbin Institute of Technology，150090 Harbin，China；3.School of Energy and Civil Engineering，Harbin University of Commerce，150028 Harbin，China；4.Guangdong Electric Design Institute，Guangzhou 510660，China）

Blockage in pressure pipelines has become a serious issue in the world.According to the basic principle ofauto⁃oscillation theory，the simplified modelis putforward for the numericalsimulation ofblockage detection.Based on the theory of transient flow，the governing equations of transients in a pipeline including blockage are established with the adoption of Dirac delta function.Non⁃dimensionalizing and linearizing the governing equation，the equations will be simplified.An analytical solution has been deduced under the fixed boundary conditions.By Fourier series analyzing，the amplitudes of each harmonic component in different periods are calculated，and the damping exponent of each harmonic component can be obtained.The results show that the blockage damping is direct ratio to the flow rate of pipe，and the location of damping has the cosine relation with damping parameters，so the location and magnitude of blockage can be fixed if two blockage damping parameters are known.

blockage in pressure pipelines；transient flow；auto oscillations；blockage damping；friction damping

TU991.0

A

0367-6234（2014）08-0045-06

2013-07-20.

国家自然科学基金资助项目（51208160）；

黑龙江省自然科学基金资助项目（QC2012C056）.

伍悦滨（1966—），女，教授.

徐 莹，joexying＠126.com.