电能回馈型负载电流模拟器非线性负载模拟研究
2014-06-24黄朝霞邹旭东黄清军邹云屏
黄朝霞 邹旭东 童 力 黄清军 王 伟 邹云屏
(1.中国船级社武汉规范研究所 武汉 430000 2.华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074)
1 引言
以背靠背结构为核心的电能回馈型负载电流模拟器(Power Energy Feedback Load Current Simulator,PEFLCS)用以实现对多种负载特性的模拟,满足单相交流电能装置的考核需求[1,2]。其前级负载模拟变换器(Load Simulation Convertor,LSC)模拟各种负载电流特性[3-6],后级并网变换器(Grid-Connected Convertor,GCC)将被试电源输出的电能高效、快速地回馈给电网,达到绿色节能的目的。
为了实现各种负载的模拟,LSC 通常采用单电流环跟踪所需模拟的负载电流指令。其中对非线性负载的精确模拟是考核PEFLCS 工作性能的重要指标。目前对PEFLCS 模拟非线性负载并未有定性、定量的分析,通常采用不控整流器作为典型非线性负载分析,并引入峰值因数(Peak Factor,PF)来表征非线性和线性负载电流的差别程度。在非线性负载电流指令的生成方法研究方面,文献[7]结合开关函数和周期函数的傅里叶级数表达的频域分析法,利用线性迭加原理,求解出每次谐波的幅值和相位,从而可以精确地再现所需非线性负载电流波形,但该方法计算繁琐,较难实现,且未建立复杂电流与PF 值之间的定量关系;文献[8]基于时域分析方法,针对不同的数学模型列写不同的状态方程,将其离散化后,通过递推公式,得到实时非线性电流波形指令,但该方法需要增加额外的设备,亦未与PF 建立联系。在非线性负载模拟电流指令的跟踪研究方面,传统的数字PI 控制器带宽有限,难以同时满足快速性和稳定性要求,目前大多数文献只是针对线性负载的电流环控制策略研究[9-11],文献[12]采用PI 控制+重复控制并联的改进重复控制器实现了对非线性负载特性的模拟,使得LSC 输入电流能够稳定地跟踪非线性负载指令,但未涉及动态特性的分析。
由于非线性负载的PF 值是考核电源带载能力的重要参数,本文首先以国标GB/T7260—3 中制定的基准非线性负载(reference non-linear load)作为LSC 对非线性负载电流特性的模拟标准,建立了PF值与非线性负载电流指令的映射关系数据库,供LSC 模拟各种PF 值的非线性负载时采用。为克服LSC 侧采用单电流环P 控制无法满足电流指令中主要次谐波在要求带宽内零增益、零相移的不足,综合P 控制的快速性和重复控制良好的跟踪特性,采用了P 控制+重复控制的复合控制策略。关于P控制+重复控制的复合控制国内外有大量研究成果[12-16],存在两种组合结构,但一般只对一种结构进行分析,哪种结构更优值得深入讨论。鉴于此,结合PEFLCS 自身功能特性,本文对比分析了P 控制与重复控制串、并联两种复合结构对LSC 控制的影响。最后成功研制了一台2.2kV·A 的PEFLCS 样机,并进行了相关稳态和动态实验验证。
2 PEFLCS 拓扑及工作原理
图1所示框中部分为PEFLCS 拓扑结构。其中,GCC 由开关管S21~S24、并网交流电感L2、并网等效电阻r2和电容C以及并网变压器T 构成,稳定直流母线电压,将能量回馈电网;LSC 由开关管S11~S14、输入交流电感L1和输入等效电阻r1构成,用于实现各种负载电流特性的模拟,为本文研究重点。

图1 电能回馈型负载电流模拟器实验电路拓扑结构Fig.1 Experimental circuit topology of the feedback-type load current simulator
由于被试电源不允许能量倒灌,同时要求LSC可以任意模拟各种负载电流特性,因此,LSC 侧通常采用单电流环控制,直接给定不同的电流指令,采用合适的控制策略,即可实现不同负载电流特性的模拟。
3 非线性负载电流指令生成方法
非线性负载电流中丰富的谐波会对各种电源设 备造成不同程度的影响和危害。通常采用峰值因数来表征非线性负载电流与线性电流的差别程度。GB/T7260—3 标准指出:“峰值因数PF 是周期量的峰值对方均根值之比。”其中方均根值就是平常所说的有效值,其表达式为
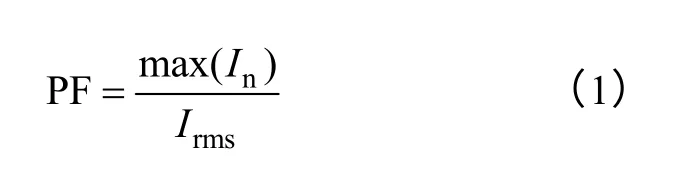
一般峰值因数最大的负载是个人计算机,约等于2.7,因而LSC 只要能模拟峰值因数为3 以下的非线性负载电流特性,就完全能满足各种被试电源的考核需求。
对被试电源带非线性负载的考核根据被试电源的情况而定。在UPS 供电的负载中多是整流滤波型,UPS 的输入也是整流滤波型。因此,IEC 标准中便制定了一个基准非线性负载。用这个基准非线性负载检验UPS 带非线性负载的能力。在UPS 国标GB/T7260—3 中,给出了这个基准非线性负载电路,如图2a 所示。

图2 典型的非线性负载示意图Fig.2 Diagram of typical nonlinear load
通过对比发现,典型的单相不控整流电路在电流断续状态下的输入电流波形与非线性系统中的死区特性非常相似,所以本文采用非线性死区特性生成的波形粗略计算出不控整流电路的开通角,将PF与所求非线性电流的开通角联系起来,指令生成方法计算方便,便于理解。
假设正弦电流为

通过死区效应后开通角为δ,由于其波形是对称的,关断角为π-δ。因此,在半个周波内的导通角为θ=π-2δ,将该导通角范围内的波形等效为以2θ为周期的正弦函数,得到有效值表达式为

将式(3)代入式(1)中

只要给定相应的PF 值,则可求出开通角δ,从而得到死区效应仿真中的导通角θ=π-2δ,将此导通角θ作为不控LCR 整流电路中二极管导通角的参考值,代入文献[17]中的不控整流电路参数求解方程式(5)中,可得到不控整流电路的开通角δo和RωC值。

选取合适的R、C值,在Matlab 中搭建不控整流电路进行仿真,计算出实际PF 值,再微调电感L即可得到精确的非线性电流波形,记录该波形并生成数组可得到相应的非线性电流指令。给定不同的PF 值,重复上述操作,可得到非线性电流波形数据表。
例如:给定PF=3,根据式(4)求得δ=1.242 7rad,则θ=0.656 2rad。将θ代入式(5)得到不控整流电路的实际开通角δo=0.986 4rad,RωC=13.895 7。若ω=314,选取C=2 350μF,可得R=18.8Ω,选取L=0.1mH,通过不控整流电路仿真,可得PF=3.381 的非线性电流波形,微调电感L=0.21mH,仿真得到PF=2.974,将此波形作为PF 值为3 的波形数据记录即可。
需要强调的是,符合峰值因数的非线性电流波形不是唯一的,不同的LCR 组合波形也会不同,但并不影响对被试电源的考核。
上述方法的思路同样适用于三角波、方波等非线性波形的生成,由于篇幅有限,不一一介绍了。图3分别所示为按上述方法计算生成的峰值因数为2.5 的LCR 不控整流电路电流、方波电流和三角波电流的指令。

图3 各种非线性电流指令Fig.3 Various nonlinear current references
4 P 控制+重复控制的复合控制策略
图4所示为LSC 采用单电流环P 控制时的控制框图。

图4 PWM 变换器电流环控制框图Fig.4 Current loop control program of PWM converter
考虑滞后一拍,电流环比例系数kpi取不同值时,单P 控制闭环传递函数伯德图如图5所示。通过分析得到[18],当kpi较大时,电流环带宽比较大,虽可以很好地跟踪非线性电流的幅值,但在中高频段会出现明显的相移,而且系统数字化后易引起中频段出现剧烈的谐振峰,使系统中出现大量的中频扰动,特别在电感值偏差较大或出现饱和的情况下,系统的中高频谐振会更严重[19]。当kpi较小时,系统带宽较小,在跟踪非线性负载电流指令时,无法保证系统在特定频段范围内具有“零相移,零增益”的效果。观察发现kpi取值为10时系统没有出现谐振峰,带宽约为1.23kHz,将近基波频率的25 倍,包含了非线性负载电流中明显的21 次谐波,动态响应良好。在基波频率处虽然衰减只有0.258dB,但是相移却达到了5.33°,由于考虑滞后一拍,在截止频率处的相移更是高达139°,为了进一步改善LSC侧对电流指令的跟踪效果,引入重复控制。

图5 单P 控制LSC 闭环传递函数伯德图Fig.5 Bode diagram of LSC with P controller
4.1 重复控制基本原理
图6所示为重复控制框图。

图6 重复控制框图Fig.6 Diagram of repetitive controller
根据图6可以得到电流环闭环传递函数,即电感电流与指令电流之比

重复控制器由重复信号发生器、周期延迟环节z-N和补偿器C(z)组成。周期延迟环节z-N的存在会造成重复控制一个基波周期的延迟。补偿器C(z)主要是提供相位补偿和幅值补偿,是重复控制器中最重要的部分,其表达式如下

式中,S(z)为补偿滤波器,若选用二阶低通滤波器可加快高频衰减,提高系统的稳定性;若选用陷波器可消除系统在截止频率附近的谐振峰;若选用超前滞后环节可调整系统的幅值相位以及带宽。zk为相位超前补偿环节,k值可以通过分别取1,2,3,…,选取与系统截止频率处需要补偿的相角最接近的k值即可。Kr为重复控制增益,用于保证系统在中高频段的稳定性[14]。
由于周期延迟环节z-N的作用,重复控制对跟踪误差的调节作用滞后一个基波周期,也就是说,重复控制无法将系统的动态响应时间缩短到小于一个基波周期的等级,这就必然会降低系统的响应速度。
为使系统控制达到快速性和稳态精度两方面的要求,工程上往往采用两种性能互补的控制方式相结合的控制策略。本文采取P 控制与重复控制相结合的复合控制策略。
4.2 P 控制+重复控制复合控制策略
如图7所示,P 控制+重复控制的复合控制有两种结构[20]。一种是P 控制并联重复控制,另一种是P 控制串联重复控制。
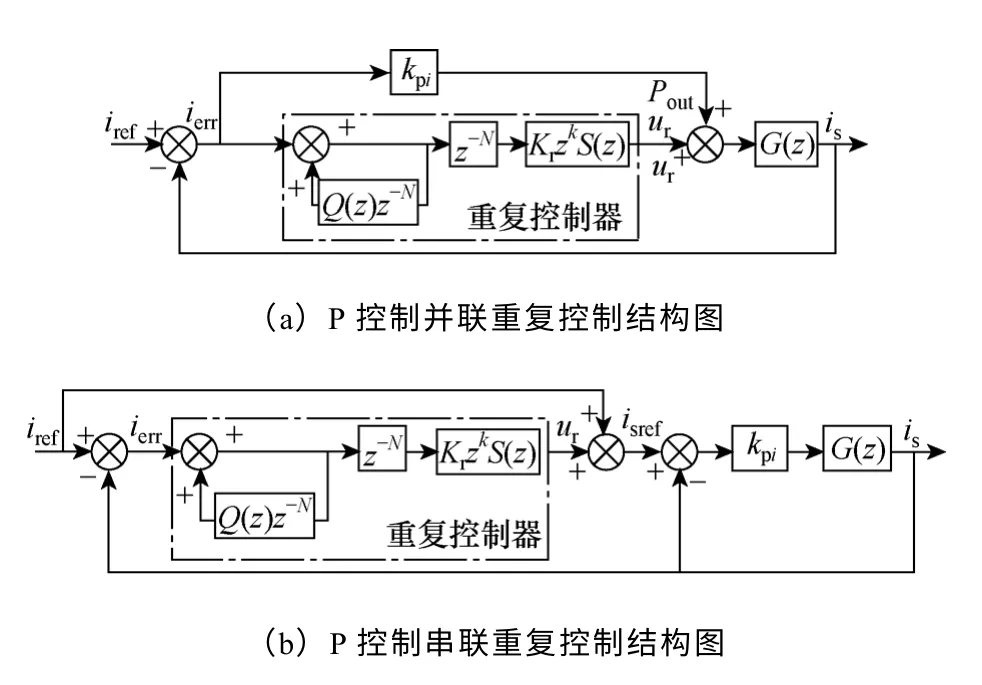
图7 复合控制框图Fig.7 The block diagram of complex controller
由图7a,并联复合控制的闭环传递函数为

相应的系统特征方程为

由图7b,串联复合控制的闭环传递函数为

相应的系统特征方程为

对比式(6)、式(8)、式(10)可得,复合控制与重复控制的主要区别在于重复控制的对象GL(z)变成了P 控制作用后的系统。并联复合控制被控对象为,相当于P 控制作用在反馈通道上的闭环传递函数;串联复合控制被控对象为,相当于单P 控制电流环闭环传递函数,串联复合结构的特征方程更直观的表达出复合结构的控制依存关系。对比式(9)与式(11)得到,并联复合控制和串联复合控制的稳定条件是一致的:一是要求单独的P 控制系统必须是稳定的;二是要求针对经P 控制器改造后的控制对象所设计的重复控制器参数必须满足系统的稳定。
将并联复合控制闭环传递函数式(8)适当变形得

式(12)与串联复合控制闭环传递函数式(10)比较发现,并联复合控制在补偿器C(z)的设计上比串联复合控制多了比例系数kpi,即串联复合控制通过在原有指令上叠加修正量ur来减小误差,使重复控制器只需抑制控制对象对原有指令的跟踪误差即可,这显著减轻了重复控制器的负担,正如图8中两种复合结构中的重复控制器幅频特性所示。

图8 串、并联重复控制器的伯德对比图Fig.8 Bode diagrams of repetitive controller with different structures
图9为校正后的电流环闭环传递函数伯德图,与图8单P 控制时的系统闭环传函伯德图GL(z)对比可知,通过复合控制后整个电流环闭环带宽可达到1.05kHz,在非线性负载主要谐波段(21 次谐波以内)内的基波倍频处实现了零增益、零相移的要求。同时,由图9可知,串、并联复合控制经过重复控制器的设计后最终趋于一致,与理论分析一致。
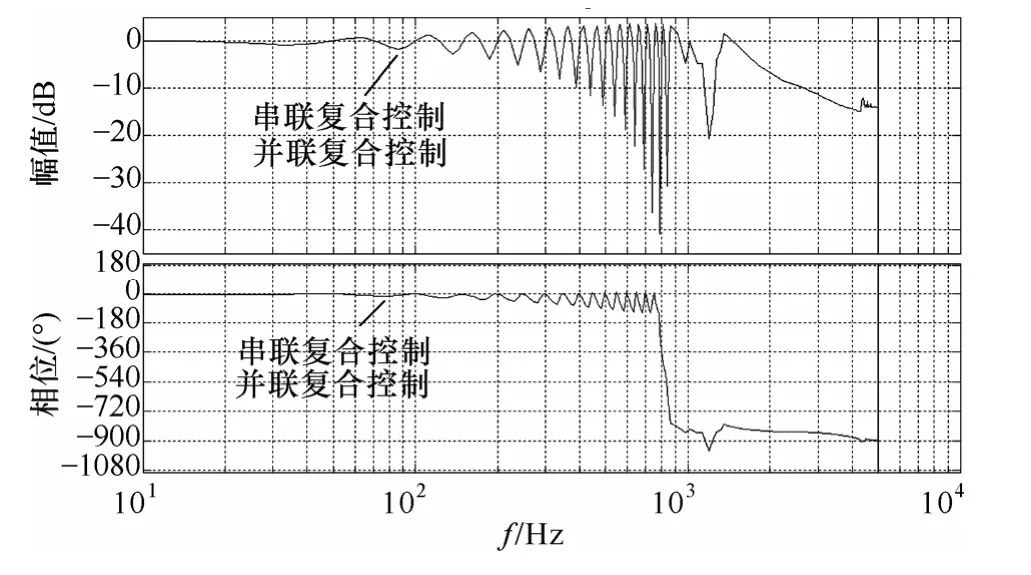
图9 串、并联复合控制电流环闭环伯德对比图Fig.9 Bode diagrams of complex controller with different structures
5 仿真与实验研究
为了验证本文的理论分析,搭建了一台2.2kV·A的电能回馈型负载电流模拟器。LSC 采用单电流环P 控制,kpi=10,GCC 采用电流内环P 控制,电压外环PI 控制的双环控制策略,电流内环Kpi=10,电压外环Kpv=0.5,Kiv=32。重复控制器参数为:Q=0.95,Kr=0.95,k=3,S1(z)为超前滞后环节,S2(z)为二阶低通滤波器。系统的电路参数见下表。

表 PEFLC 系统参数Tab. Parameters of the PEFLCS system
5.1 仿真分析
图10为负载电流模拟器模拟非线性负载波峰因数为2.5时采用不同控制方式的稳态仿真。由虚线圈部分可以发现,稳态时复合控制比单P 控制的跟踪效果好很多,而串联复合控制和并联复合控制效果几乎相同。

图10 PEFLCS 模拟波峰因数为2.5LCR 不控整流非线性负载电流指令及其跟踪波形Fig.10 Control effects by different controllers when simulating PF=2.5 nonlinear load by PEFLCS
图11为ACEL 模拟纯阻性负载时,指令从空载到满载LSC 侧采用不同控制方式时的电流跟踪波形。可以看出,单P 控制的动态特性比复合控制好,在一个周波内就实现了快速跟踪,而复合控制由于重复控制的作用在发生突变的第二个周波内电流峰值处出现了严重的畸变,需要多个基波周期才能消除。

图11 PEFLCS 空载-满载SC 侧采用不同控制方式 动态特性分析Fig.11 Different controller dynamic experiment analysis with different controllers
由于串联复合控制与并联复合控制对输入电流的控制效果类似,图12只给出P 控制与串联复合控制分别模拟三角波和方波时的仿真波形,验证了系统在复合控制条件下可以较好地模拟三角波和方波。

图12 PEFLCS 模拟波峰因数为2.5 三角波和 方波及其跟踪波形Fig.12 Control effects by different controllers when simulating PF=2.5 nonlinear load by PEFLCS
5.2 实验验证
图13a 给出了采用单P 电流环控制和复合控制后的三角波电流指令跟踪对比图。显然,采用复合控制后,系统模拟非线性负载时的电流稳态跟踪效果要好得多。且由于重复控制器的校正使得串联复合控制和并联复合控制的跟踪效果相似,但串联复合控制重复控制器的负担相对较轻,因而后续实验以串联复合控制为主。图13b 给出了系统模拟LCR不控整流时采用P 控制和串联复合控制的对比图,复合控制的控制效果明显优于单P 控制。由于模拟的非线性负载峰值因数较高,谐波含量丰富,导致三次谐波含量陡增,输入电压波形畸变。说明高峰值因数的非线性负载模拟是考核被试电源质量的重要手段,也是对电能回馈型负载电流模拟器负载模拟功能的一大考验。

图13 单P 电流环控制和复合控制后的 非线性电流指令跟踪对比图Fig.13 Effects contrast diagram of nonlinear current reference with different controller
图14为LSC 采用复合控制时模拟峰值因数PF分别为1.5、2.0、2.5 和3.0 的LCR 不控整流非线性负载电流特性示意图。说明系统能够实现峰值因数3.0 以下的任意LCR 不控整流非线性负载的模拟。满足被试电源的考核需求。
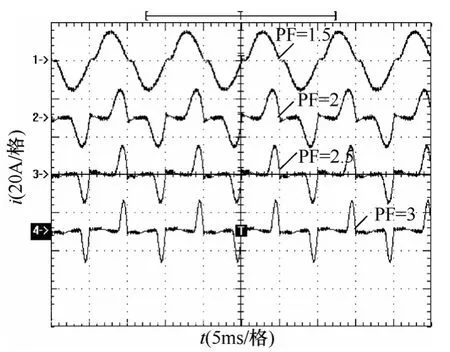
图14 不同峰值因数的LCR 不控整流非线性 电流实验波形Fig.14 Nonlinear current waveforms with different PF in LCR un-control rectifier
图15为负载电流模拟器艺分别采用单P 控制和串联复合控制时LSC 模拟线性纯阻负载时输入端口特性的实验对比图。由图15b、图15e 李萨如图对比发现,复合控制系统的过零点重合度非常高,校正了单P 控制出现的部分相移,达到了功率因数为1 的要求。图15c、图15f 说明复合控制在校正相移的同时也改善了电流波形质量,较好地实现了纯阻性负载的模拟。

图15 采用单P 控制和串联复合控制时的输入端口特性(第一行:单P 控制;第二行:复合控制)Fig.15 Experimental results with P control(first row)and complex control(second row)
图16是LSC 侧分别采用单P 控制和串联复合控制时系统突加负载整体波形实验对比。从波形对比图看出,串联复合控制的动态响应时间略大于单P 控制,从50ms 左右增加到了100ms。可见,采用单P 控制+重复控制的复合控制策略在动态响应方面略微差于单P 控制,与理论相符。

图16 P 控制和串联复合控制动态实验分析(空载到满载)Fig.16 Dynamic experiment analysis with P control and complex control(no load to full load)
6 结论
本文提出了一种基于峰值因数(PF)的非线性负载电流指令的生成方法。该方法可以精确生成峰值因数3.0 以下的各种LCR 不控整流型电流指令、三角波和方波等非线性电流指令。
在此基础上,采用P 控制+重复控制的复合控制策略实现非线性负载电流指令的无静差跟踪,从理论、仿真和实验多方面对比了P 控制、串联复合控制和并联复合控制的区别,得到以下结论:
(1)串、并联复合控制在稳态时比P 控制更好地跟踪了非线性负载电流指令;但动态时模拟线性负载突加的情况下,会造成输入电流畸变,需要多个周波才能完全跟踪上指令电流。
(2)在控制结构上,串联复合控制比并联复合控制更直观地体现了复合结构的控制依存关系,设计步骤相对简单;在闭环特性上,通过重复控制器的设计校正后,串联复合控制与并联复合控制趋于一致,通过仿真对比验证,由于串联复合控制中的重复控制器的负担较轻,串联复合控制对控制系统的控制效果比并联复合控制略好。
仿真和实验均验证了PEFLCS 可以较好地实现LCR 不控整流型电流指令、三角波和方波等非线性电流指令的模拟。
[1]Lin C L,Tsai M T,Tsai W I,et al.A study on the burn-in test of charger with load bank elimination[C].Proceedings of IEEE IAS,1995:72-77.
[2]Lin C L,Tsai M T,Tsai W I,et al.Consumption power feedback unit for power electronics burn-in test[J].IEEE Transactions on Industrial Electronics,1997,44(2):157-166.
[3]Chang M Y,Lin J Y,Jung S L,et al.Design and implementation of a real-time lossless dynamic elec- tronic load simulator[C].Proceedings of IEEE Power Electronics Specialists Conference,1997:734-739.
[4]贾贵玺,齐乐,张炳达.电力系统动态模拟中可控负载的设计[J].电力系统及其自动化学报,2005,17(6):95-99.
Jia Guixi,Qi Le,Zhang Bingda.Design of controllable load for power system dynamic simulation[J].Procee- dings of the CSU–EPSA,2005,17(6):95-99.
[5]赵剑锋,潘诗锋,王浔.大功率能量回馈型交流电子负载及其在电力系统动模实验中的应用[J].电工技术学报,2006,21(12):35-39.
Zhao Jianfeng,Pan Shifeng,Wang Xun.High power energy feedback AC electronic load and its application in power system dynamic physical simulation[J].Transactions of China Electrotechnical Society,2006,21(12):35-39.
[6]周群,毛承雄,陆继明,等.电力系统负载的数字模拟[J].电力系统及其自动化学报,2008,22(3):124-128.
Zhou Qun,Mao Chengxiong,Lu Jiming.et al.Digital simulation of power system load[J].Proceedings of the CSU–EPSA,2008,22(3):124-128.
[7]陈敏.非线性负载条件下的逆变器特性研究[D].杭州:浙江大学,2006.
[8]王亚玲.能馈式交流电子模拟负载的研究[D].济南:山东大学,2009.
[9]Li Fen,Zou Yunping,Chen Wei,et al.Comparison of current control techniques for single-phase voltage- source PWM rectifiers[C].Proceeding of IEEE International Conference on Industrial Technology,2008:1-4.
[10]Zhang Zheyu,Zou Yunping,Wu Zhenxing.Design and research of three-phase power electronic load[C].2009 IEEE 6th International Power Electronics and Motion Control Conference,WuHan,2009:1798- 1802.
[11]吴振兴,邹云屏,张允,等.单相PWM 整流器输入电流波形的改善技术[J].高电压技术,2008,34(3):603-608.
Wu Zhenxing,Zou Yunping,Zhang Yun,et al.Supply current waveform improvement technique for single-phase PWM rectifier[J].High Voltage Enginee- ring,2008,34(3):603-608.
[12]王成智,邹旭东,许赟,等.采用改进重复控制的大功率电力电子负载[J].中国电机工程学报,2009,29(12):1-9.
Wang Chengzhi,Zou Xudong,Xu Yun,et al.Improved repetitive control scheme for power electronic load[J].Proceedings of the CSEE,2009,29(12):1-9.
[13]Zhang Kai,Kang Yong,Xiong Jian,et al.Direct repetitive control of SPWM inverter for UPS purpose[J].IEEE Transactions on Power Electronics,2003,18(3):784-792.
[14]魏学良,戴珂,方昕,等.三相并联型有源电力滤波器补偿电流性能分析与改进[J].中国电机工程学报,2007,27(28):113-119.
Wei Xueliang,Dai Ke,Fang Xin,et al.Performance analysis and improvement of output for three phase shunt active power filter[J].Proceedings of the CSEE,2007,27(28):113-119.
[15]Garcia-Cerrada A,Pinzon-Ardila O,Feliu-Batlle V,et al.Application of a repetitive controller for a three- phase active power filter[J].IEEE Transactions on Power Electronics,2007,22(1):237-246.
[16]吴振兴,邹旭东,黄清军,等.三相电力电子负载并网变换器研究[J].中国电机工程学报,2010,30(24):1-7.
Wu Zhenxing,Zou Xudong,Huang Qingjun,et al.Research on grid connection converter of three-phase power electronic load[J].Proceedings of the CSEE,2010,30(24):1-7.
[17]陈坚.电力电子学——电力电子变换和控制技术[M].北京:高等教育出版社,2002.
[18]黄朝霞,邹云屏,王成智.基于PI 控制的电力电子负载[J].高电压技术,2009,35(6):1451-1456.
Huang Zhaoxia,Zou Yunping,Wang Chengzhi.Research on the power electronic load based on PI control[J].High Voltage Engineering,2009,35(6):1451-1456.
[19]王兆安,黄俊.电力电子技术.北京:机械工业出版社,2000.
[20]王斯然,吕征宇.LCL 型并网逆变器中重复控制方法研究[J].中国电机工程学报,2010,30(27):69-75.
Wang Siran,Lü Zhengyu.Research on repetitive control method applied to grid-connected inverter with LCL filter[J].Proceedings of the CSEE,2010,30(27):69-75.
