基于Contourlet变换的高分辨率遥感影像分割

马 红

(重庆市勘测院,重庆 400020)

基于Contourlet变换的高分辨率遥感影像分割

马 红∗

(重庆市勘测院,重庆 400020)

鉴于Coutourlet变换能够充分提取影像中的高维边缘和轮廓信息,并结合低频信息构成影像特征。本文结合高分辨率遥感影像丰富的光谱特征和独特的纹理特征,提出一种基于Contourlet变换的影像分割方法。通过设置Contourlet变换不同分解层数、不同移动窗口进行对比实验,验证了本文方法的可行性,并通过与基于二维小波变换的影像分割进行对比实验,证明本文方法能够得到更平滑和连续的效果。

Contourlet变换;特征提取;影像分割

1 引 言

遥感影像分割是对影像中感兴趣的目标进行检测和量测,以获得他们的客观信息,从而建立对影像的描述[1],是遥感影像处理中的重要技术,为其后的遥感影像分析、影像识别等处理阶段做准备。通过综合不同尺度的图像信息,把精细尺度的精确性与粗糙尺度的易分割性统一起来,能得到更好的分割效果。

国内外众多学者从影像特征入手,对高分辨率遥感影像分割进行了研究,Dunn等利用二维Gabor小波分析了图像纹理特征,分析了山脊、山谷等纹理的不同,并用于分割图像[2];CHOI等人提出了小波域隐马尔可夫树模型的图像分割方法[3]。对含点状奇异性的目标小波函数是最优基,对线状奇异性的目标小波不是最优和最稀疏的函数表示方法;研究发现,小波变换在高维情况下无法充分利用图像的边缘和轮廓信息。Minh.N和Martin Vetterli提出的Contourlet变换则是一种多尺度几何分析工具,在表达图像时可以同时满足视觉信息描述的三个基本要素(尺度、空间和方向信息),对于图像边缘轮廓和纹理特征的表达有独到的优势[4]。本文利用Contourlet变换分解影像特征,利用模糊C均值方法进行分割,实验结果表明该方法是可行的。

2 Contourlet变换原理

Contourlet变换是一种多分辨率、局域的、方向的影像表示方法,其基的支撑区间具有随尺度而长宽比变化的“长条形结构”[5]。实现可以看成是两个步骤:拉普拉斯金字塔[6,7](Laplacian pyramid,LP)分解和方向滤波器组[8](directional filter bank,DFB)。前者将原始图像进行高斯金字塔分解,每一级分解分别得到一个低频图像和高频图像,然后通过差值得到LP结果。然后,进一步将低频图像继续进行拉普拉斯分解,高频图像(细节部分)则采用方向组滤波器进行滤波,形成塔式方向滤波器组。图1为Contourlet变换分解的流程。

图1 Contourlet变换分解结构

3 基于Contourlet变换的影像分割流程

本文使用Contourlet变化进行影像分割具体流程如下,首先对影像进行Contourlet分解,得到单一尺度或多尺度的低频及各个方向高频子带系数,根据子带系数建立影像特征,得到特征度量,最后以提取到的特征为基础进行影像分割,图2为本文方法的操作流程。

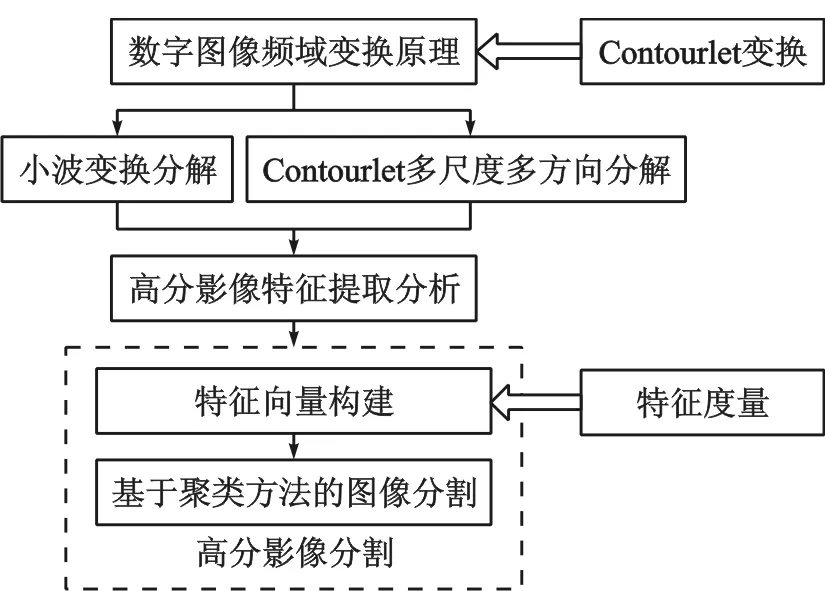
图2 基于Contourlet变换的高分辨率遥感影像分割流程

3.1 利用Contourlet变换构建影像特征

鉴于Contourlet变换可以获得不同的方向子带信息,采用Contourlet变换对影像进行多方向分解,采用类似于小波变换的纹理特征提取方法来获得相应的影像特征。为了能对所得的特征向量进行归一化处理,对像素对于像素(i,j)的特征向量的k个特征分量F(i,j,k),进行归一化处理[9],如式(1):

计算得到的子带能量测度包括一个低频子带和每个尺度上的高频子带;根据分解层数和每层分解个数可以确定特征向量的维数。子带的能量测度为子带系数的数学期望,如式(2):

其中,子带大小为M×N,m(i,j)为分解子带中(i,j)位置的系数值。

将图像行列信息作为纹理特征向量,即引入了空间关系,则像素(i,j)的特征向量为3l+1组特征分量加上分量i和j。

3.2 利用相关系数度量影像特征

特征度量即分析特征之间的相似性。为兼顾全局效果,本文通过计算特征之间的相关系数来分析影像特征之间的相似性。引入到皮尔逊相关系数r(其中r∈[-1,1])来分析两个特征向量之间的线性相关度。假定x,y是两个不同的特征向量,n是特征的维数。x,y的相关系数值r如式(3):

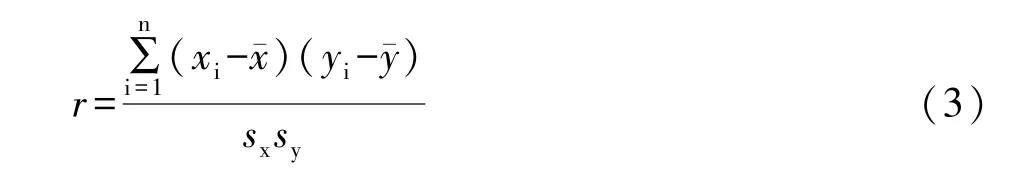
其中,¯x和¯y分别表示向量x和y的平均值,sx和sy分别表示向量x和y的标准差。通过计算特征之间的相关系数,定义合理的阈值,剔除相关性较大的特征向量,利用相关性较小的特征向量进行影像分割。

3.3 利用模糊C均值进行影像分割

针对所获得的影像特征向量,采用模糊C均值(FCM)方法进行图像分割。本文利用Bezdek的推广进行FCM分割[10],如式(4):

其中,m是模糊加权指数(m≥1)。

聚类准则是使目标函数Jm达到极小值,根据拉格朗日乘数法求得此时的模糊C-划分矩阵U=[μij]和聚类中心V。

4 实验结果及分析

实验数据如图3所示,为WordView-2卫星全色影像,空间分辨率为0.5 m,影像中主要有河流、道路以及不同种类的植被。分别采用Contourlet变换和小波变换对影像进行分解,利用3.1中得到特征值,最后再利用3.3节所述的模糊C均值方法对特征值进行分割,从而完成对影像的分割。

实验过程中,对每个像素,取自身及其一定邻域(即为移动窗口)内的像素进行Contourlet变换,获得变换结果进一步得到的特征向量作为该像素的特征向量。为了与二维小波分解进行对比,取同样窗口内德像素进行小波分解,并得到同一像素的特征向量值。对于小波变换,使用小波基为‘db4’(即Daubechies小波[12])。对于Contourlet变换,使用Contourlet Toolbox[11]进行计算。Contoulet变换中金字塔变换的滤波器是‘9-7’[11,13],方向滤波器为‘pkva’[11,13],文献[13]指出,这两种滤波器使得Contourlet变换能够达到更好的分离噪声的效果。Contourlet变换每一层使用的分解方向数目为8。

图3 实验原始数据

图4 表示的是移动窗口大小为32×32的1层的Contourlet分解与小波分解,窗口大小为32×32的2层Contourlet分解与小波分解,并进一步提取特征值,最终进行影像分割得到的分割结果。能量子带按式(2)计算得到特征向量,并采用模糊C均值方法进行分割得到分割结果,对应图4中的a、b、c和d。

图4 基于Contourlet分解与小波分解的影像分割对比(移动窗口32×32)

图5 表示的是移动窗口大小为16×16的1层的Contourlet分解与小波分解,窗口大小为16×16的2层Contourlet分解与小波分解,并进一步提取特征值,最终进行影像分割得到的分割结果。子带按式(2)计算得到特征向量,特征度量使用式(3),最后使用模糊C均值方法得到分割结果对应图5中的a、b、c和d。

图5 基于Contourlet分解与小波分解的影像分割对比(移动窗口16×16)

图4 使用的移动窗口是32×32,图5用的移动窗口大小为16×16,分别从分解层数、移动窗口与分解方法三个角度进行比较,可以得到如下结论。

(1)分解层数对比,将图4的(a)(b)与图4的(c) (d)以及将图5的(a)(b)与图5的(c)(d)对比可得出,无论是小波变换还是Contourlet变换,分解层数多的获得的特征向量用于分割的结果优于分解层数少的影像分割结果。

(2)移动窗口对比,由图4(a)(b)(c)(d)和图5 (a)(b)(c)(d)对比可得出,16×16的窗口分割结果优于32×32的窗口分割结果,这是因为窗口过大,窗口内的元素不够纯净,产生了带状边缘效应。

(3)分解方法对比,对比图4(a)与(b)、图4(c)与(d)、图5(a)与(b)、图5的(c)与(d)可得出,基于Contourlet变化所获得的特征向量分割结果比基于小波变化所得到的特征向量分割更加平滑,空间上更加连续,同时影像的细节也得到较好的体现。

5 结 语

本文提出基于Contourlet变化的影像特征提取,并对提取特征进行合理取舍,基于获得的影像特征,采用模糊C均值的聚类分析方法对影像进行分割。通过分解层数对比试验和移动窗口对比试验结果可以看出,选择合适的移动窗口和适宜的分解层数,采用Contourlet变化可以获得较好的结果。通过分解方法的对比试验可以看出,在相同的分解层数和移动窗口下,本文基于Contourlet变化的分解优于传统小波分解,能够得到更加平滑和连续的效果,也可以更好地突出影像细节。

[1] 贾永红.数字图像处理[D].武汉:武汉大学出版社, 2003.

[2] Dunn D,Higgins W E,Wakeley J.Texture segmentation using 2-D Gabor elementary functions[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,1994,16 (2):130～149.

[3] Choi H,Richard G,Baraniuk.Multiscale Image Segmentation Using Wavelet Domain Hidden Markov Models[J].IEEETransactions on Image Processing,2001,10(9):1309～1321.

[4] 程起敏.遥感图像检索技术[M].武汉大学出版社, 2011.

[5] 肖易寒,席志红等.Contourlet变换的图像分割[J].哈尔滨理工大学学报,2011,5(16):101～105.

[6] Do M N,Vetterli M.Framing Pyramids[J].IEEE Trans on Signal Processing,2003,51(9):2329～2342.

[7] Burt P,Adelson E.The Laplacian pyramid as a compact image code[J].Communications,IEEE Transactions on,1983, 31(4):532～540.

[8] Do M N,Vetterli M.The Contourlet Transform:An Efficient Directional Multiresolution Image Representation[J].IEEE Trans on Image Processing,2005,14(12):2091～2106.

[9] 宫志华.基于超完备Contourlet的纹理图像分割[D].西安:西安电子科技大学,2010.

[10] 高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004.

[11] Contourlet Toolbox(Version 2.0)[OL/DB].http://www.ifp.uiuc.edu/～minhdo/software/.

[12] 李登峰,杨晓慧.小波基础理论和应用实例[M].高等教育出版社,2010.

[13] 李洪均,赵志敏,陈远等.Contourlet变换中不同滤波器对图像去噪效果的研究[J].红外技术,2008,30(8):450～453.

High-resolution Romote Sensing Images Segmentation Based on Contourlet Transform

Ma Hong
(Chongqing Survey Institute,Chongqing 400020,China)

Because the edge and contour in the image of high dimension was fully captured by the Contourlet transform,the paper presents a image segmentation based on the Contourlet transform by integrating theimgage’s rich spectral characteristics and unique texture characteristics.Compared to the imageSegmentation method based on Wavelet Transform,obtain better result.

contourlet transform;feature extraction;image segmentation

2014—03—04

马红(1987—),女,工程师,主要从事遥感影像处理及应用研究工作。

十二五国家科技支撑计划(2011BAH12B07-03)