平面波展开法在质量分数测量上的应用研究

阿不都热苏力·阿不都热西提，帕孜来提，帕尔哈提·米吉提

（新疆大学物理科学与技术学院，乌鲁木齐830046）

平面波展开法在质量分数测量上的应用研究

阿不都热苏力·阿不都热西提，帕孜来提，帕尔哈提·米吉提

（新疆大学物理科学与技术学院，乌鲁木齐830046）

为了提出测定果糖质量分数的新方案，采用光子晶体平面波展开法进行了理论分析和数值模拟。通过研究以硅半导体材料为背景介质周期性排列空气孔圆柱构成的光子晶体，分别取得了正方晶格和三角晶格的空气孔结构光子晶体的TE模、TM模禁带结构特性。结果表明，在高频率区域，2维正方晶格或三角晶格结构各向同性光子晶体的光子带隙随待测质量分数不同是单调变化的；同时，晶格结构对光子带隙有一定的影响，不论是在正方结构还是三角结构光子晶体中，TE模带隙都比TM模大得多。这对质量分数测量和高血糖患者的临床应用有一定的指导作用。

材料；光子带隙；平面波展开；质量分数；果糖

引 言

光子晶体（photonic crystal，PC）作为一种新型人工材料，又称为光子带隙材料。所谓光子晶体就是使某一种折射率的材料周期性地嵌入到另一种光传输材料中，而得到的晶体结构。由于光线入射到不同介质的界面会产生折射或反射，当某一种材料周期地分布在另一种不同折射率的材料中时，光线在传播过程中也会遭到这种周期结构的反射或折射，使某一能量范围的光线不能通过，从而导致某一频率范围的光线的阻断。

光子晶体的概念是1987年分别由JOHN［1］和YABLONOVICH［2］等人提出来的。它是以传统的晶体概念作为依据的。光子晶体中介质折射率的周期性变化对光的影响类似于凝聚态物质中周期性势场对电子的影响。据大家所知，在半导体材料中电子具有能隙和能带的特性，在光子晶体中也存在光子能带和能隙的特征，只有那些频率在光子能带的光才能通过光子晶体，而那些频率在光子带隙的光则会被禁止传播。光子带隙的存在导致了光子晶体许多崭新的物理性质，光子晶体广阔的应用前景已成为当今世界范围的研究热点，也得到了迅速的发展。

光子晶体能带结构方面主要有3种计算方法：平面波展开法［3］、传输矩阵法和有限时域差分法［4-5］。目前各种电磁波段在各种光子禁带结构的应用设计和数字模拟技术及制备工艺技术已成为材料科学研究的热点。同时糖类化合物在药物、生物、催化及环境等相关领域具有重要作用，有关糖类的研究也是一个重要课题［6］。在研究电解质溶液行为的理论中，作为媒介的介电常数具有重要意义。而光子晶体将在研究果糖等糖类的研究中有重要的应用价值。

本文中采用平面波展开方法，以果糖等材料的水溶液作为空气孔中的介质材料，计算了2维正方、三角排列介质柱及空气孔结构光子晶体的带隙。首次考虑了填充溶液、晶格结构、介电常数、质量分数及其温度对最大绝对帯隙的影响，提出了用光子晶体禁带特性来测量果糖溶液的新法，为光子晶体禁带理论临床应用提供一定的理论依据［7］。

1 光子晶体的电磁波理论

2维光子晶体与波导的情况相类似，可以定义为两种模式，即TE模式和TM模式。

假设电磁波在两种不同相对介电常数的2维光子晶体中传播，此时电磁波的传播分解为两个相互独立的方程来描述。

以下两式分别为只含电场或磁场的主方程式［8-13］：

式中，c表示为光速，ω为本征频率。这两个基本方程形式上与量子力学中的Schödinger方程很相似，电磁场在光子晶体中的传播可由上述任一个方程来确定。为求解方便，本文中磁场方程是由H→（波方法来求解，而电场方程是由E→（波方法来求解。

Fig.1 Model of2-D lattice structure

将（3）式～（5）式代入（1）式或（2）式，分别可得TM和TE偏振态下的特征方程分别为：

（6）式或（7）式中的介电常数可表示为：

式中，J1为1阶贝塞尔函数，f为填充因子（正方晶格f＝三角晶格f＝，a为晶格常数），ε是a空气孔的介电常数，εb是背景材料的介电常数。将（8）式代入（6）式和（7）式，即可求出E偏振和H偏振的本征频率ω。

2 数值计算结果

本文中对正方晶格和三角晶格的空气孔结构光子晶体的TE模、TM模禁带特性进行研究，分析了填充比和果糖质量分数对禁带的影响。在如图1a所示的晶体结构中，注入圆柱形空气孔的果糖介电常数为εa＝1.8031，背景材料的介电常数为εb＝11.7，空气孔的半径为r＝0.4a，晶格常数a＝1μm，模数为n＝15，果糖质量分数为0.075。图2和图3分别为空气孔在电介质中按正方和三角晶格形式排列的光子晶体带隙结构图。图中纵坐标采用归一化的无量纲频率ωa／（2πc），而横坐标采用归一化的Bloch波矢k，为便于比较，分别用TE模式和TM模式来表示。从图中可以看出，正方晶格TE模有2个能隙，Δ表示的是带隙在总的能带中占有的百分比，即带隙为0.264～0.269，Δ＝1.5%；带隙为0.493～0.494，Δ＝0.1%；而对于TM模式出现一个带隙，即带隙为0.220～0.221，Δ＝0.2%；出现的带隙宽度也比较窄，从TE模式的第一带隙和TM模式的第一带隙之间的带隙情形看，不出现多重带隙的绝对光子禁带。三角晶格TE模有2个能隙：带隙为0.249～0.350，Δ＝33.8%；带隙为0.800～0.811，Δ＝1.4%；而对于TM模式出现一个带隙，即带隙为0.663～0.667，Δ＝2.2%；虽然在三角晶格结构中更容易形成带隙，出现的带隙宽度也比较宽，但是不出现多重带隙的绝对光子禁带。

Fig.2 Dispersion diagram of the square lattice（εa＝1.8031，εb＝11.7）

改变相对介质常数，以介质常数较大的Si半导体材料（εb＝11.7）为背景，使空气圆柱在Si介质中呈正方晶格或三角晶格的2维光子晶体。当晶格常数a＝1μm，空气柱半径为r＝0.4μm，模数n＝15，果糖质量分数为0.4时，TE和TM偏振的带隙结构图如图4和图5所示。从图4和图5可以看出，增加介质空气孔中填充的果糖质量分数和介电常数，对正方晶格材料中出现的TE模有一个能隙，即带隙为0.263～0.264，Δ＝0.3%；而对于TM模式未出现带隙；在TE模带隙中出现的带隙宽度比原来变窄。从三角晶格结构图也发现，TE模的能隙虽然比较宽，但是比改变质量分数和介电常数前的宽度变窄，即带隙0.247～0.341，Δ＝31.8%；带隙为0.794～0.802，Δ＝1.0%；而对于TM模式出现一个带隙，即带隙为0.659～0.668，Δ＝1.5%。

Fig.3 Dispersion diagram of the triangular lattice（εa＝1.8031，εb＝11.7）

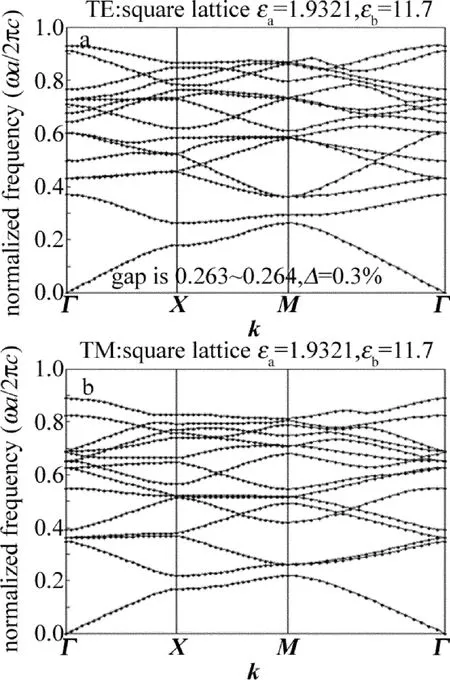
Fig.4 Dispersion diagram of the square lattice（εa＝1.9321，εb＝11.7）

Table 1 The dielectric constant of the fructose solutions of different mass fraction and lattice structure（273.15K）

由上述模拟结构来看，填充比一定，光子晶体带隙宽度并非随着质量分数和介电常数增大总是增大，而是减少。不论是正方晶格还是三角晶格，TE模在空气孔型光子晶体中更容易形成带隙，且出现的带隙较宽，带隙数目多；TM模的带隙数目较少且带隙较窄。

由不同质量分数和介电常数情况下，通过数值模拟计算，把所得数据汇制成表格，见表1。从表1可以看出，当注入圆柱空气孔的质量分数和介电常数分别由0.075到0.40和1.8031到1.9321变化时，以Si背景的光子晶体都存在光子带隙，但是未出现TE模和TM模带隙相互重叠的完全光子带隙（因为TM模的带隙较窄，表1中只给出TE模的数据）。如图6所示，当空气孔中质量分数和介电常数变增大时，不论是正方晶格还是三角晶格TE模的最大带隙宽度逐渐减少。

Fig.5 Dispersion diagram of the triangular lattice（εa＝1.9321，εb＝11.7）

3 结 论

根据平面波展开法，研究和计算了不同质量分数果糖溶液在正方晶格和三角晶格光子晶体中的光子带隙变化关系。计算发现，将通过改变由玻璃板中钻孔的空气孔2维光子晶体尺寸和间隔可以改变材料的光子带隙。此外，如果改变空气孔的介电常数，如填入一些其它材料，光子带隙也发生变化。结果表明，TE模式在圆形空气孔结构的光子晶体中更容易形成带隙，而TE模式下，光子带隙随质量分数的不同而发生变化，也就是光子带隙随质量分数的增加而变窄。同时，晶格结构对光子带隙有一定的影响。不论是正方结构还是三角结构光子晶体下，TE模带隙都比TM模大得多。这些结论为2维光子晶体质量分数测量仪的设计及其应用提供很好的理论依据，为作者正在设计中的光子晶体质量分数测量仪提供了有用的理论依据。

［1］ JOHN S.Strong localization of photon in certain disordered dielectric super lattice［J］.Physical Review Letters，1987，58（23）：2486-2489.

［2］ YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Physical Review Letters，1987，58（20）：2059-2062.

［3］ LIW.Study on band gap and waveguide coupling characteristics of air pattern photonic crystal［J］.Laser Thechnology，2012，36（2）：228-229（in Chinese）.

［4］ LIX，YANGM，GUO Sh，et al.characteristics of photonic crystal waveguides with random media［J］.Chinese Journal of Lasers，2012，39（10）：1-5（in Chinese）.

［5］ YAN M B，FU Zh T，WANGW Y.Study on transmission properties of2-D super-lattice photonic crystals［J］.Laser Thechnology，2012，36（1）：77-79（in Chinese）.

［6］ CHEN Y J，ZHUO K L，KANG L，et al.Dielectric constants for binary saccharide-water solutions at 278.15～313.15K［J］.Acta Physica Chimica Sinica，2008，24（1）：91-96（in Chinese）.

［7］ GOPINATH P，SUKANTA K T.A novel method for measurement of concentration using two dimensional Photonic crystal structures［J］.Optics Communications，2012，285（10）：2765-2768.

［8］ PLIHAL M，SHAMBROOK A，MARADUDIN A A，et al.Two-dimensional photonic band structures［J］.Optics Communications，1991，80（3）：199-204.

［9］ XIE D H，YANG H，YU Ch Y，et al.Band gap characteristics of 2-dphotonic crystals constructed with a triangular lattice of dielectric rods［J］.Journal of Xian University of Posts and Telecommunication，2012，17（2）：53-56（in Chinese）.

［10］ ABUDOUREXITI A，MIJIT P.Two dimensional photonic band structure：the square lattice［J］.Journal of Xinjiang University，2003，20（1）：32-35（in Chinese）.

［11］ YUAN G F，HAN L H，YU Ch Y，et al.Two-dimensional photonic crystal band gap characteristics［J］.Acta Physica Sinica，2011，60（30）：1-5（in Chinese）.

［12］ LIA P，WANG A Q，JIY J.Optimal design of2-D columnar photonic crystal with square lattice and large bandgap［J］.Laser Thechnology，2012，36（4）：508-511（in Chinese）.

［13］ LIU J，YAN K Zh，ZHAO Y L，et al.Research of complete band gap of2-D compound square lattice structure［J］.Laser Thechnology，2010，34（5）：653-656（in Chinese）.

Application of plane wave expansion method in measurement of mass fraction

ABUDOUREXITI·Abudouresuli，PAZILAITI，MIJITI·Paerhati
（School of Physics and Technology，Xinjiang University，Urumqi830046，China）

In order to propose a novel method to measure the mass fraction of fructose，plane wave expansion method for photonic crystal was adopted.A 2-D photonic crystal with a square lattice and triangle lattice of circular cylinders was designed in the Si background semiconductor material.The TE mode and TM mode band gap structure characteristics of square lattice and triangular lattice air hole structure photonic crystal were achieved.The results show that for isotropic photonic crystal of either square or triangular array arrangement，it is easier for the dielectric air type photonic crystal to form TE-polarized mode band gap in high-frequency region.Lattice structure has a certain impact on photonic band gap，TE mode band gap is much larger than the TM mode in both square and triangular structure photonic crystal.The photonic band gap changes with the difference of the mass fraction of the fructose solutions，which are used as the dielectric material in the air hole.

materials；photonic band gap；plane wave expansion；mass fraction；fructose

O734

A

10.7510／jgjs.issn.1001-3806.2014.01.014

1001-3806（2014）01-0065-05

国家自然科学基金资助项目（11164030）

阿不都热苏力·阿不都热西提（1961-），男，工学博士，教授，主要从事光子晶体的应用研究。

E-mail：abdrusul＠sina.com

2013-03-07；

2013-04-02