零点位于直线上的亚纯函数的正规定则

童晓丽， 刘晓俊

（上海理工大学理学院，上海 200093）

零点位于直线上的亚纯函数的正规定则

童晓丽， 刘晓俊

（上海理工大学理学院，上海 200093）

讨论了亚纯函数的零点分布在直线上的亚纯函数的正规性，得到：设F是定义在单位圆盘D上的亚纯函数族，若存在M≥0，使得对于F中任意的亚纯函数f满足f的零点分布在一直线上，其极点重级m≥3（m∈ℤ+），且f′（z）不取1，当f取值0时，f′（z）的模不大于M，则F在区域D内是正规的.

亚纯函数；零点；正规族

1 问题的提出

Bloch原理曾经提出：设P是一个亚纯函数的性质，若亚纯函数f在复平面ℂ上满足性质P，即〈f，ℂ〉∈P，则必有f≡常数.那么对于区域D上的亚纯函数族F，它的每一个元素f在区域D上满足性质P，即〈f，D〉∈P，则F在区域D上正规.例如，可取性质1为：P1=｛f≠0，f（k）≠1，k∈ℤ+｝，1959年，Hayman［1］证明了如下的Picard型定理：

定理1设f为复平面ℂ上的亚纯函数，若f∈P1，则f≡常数.

相应地，在1979年顾永兴［2］证明了对应的正规定则：

定理2设F为区域D⊂ℂ内的亚纯函数族，k≥1是正整数，若对于任意f∈F，f∈P1，则F在D内正规.

由此可见，上述性质1满足Bloch原理.再例如，取性质2为：P2=｛f的零点重级≥k+1，其极点均为重级，f（k）≠1｝，1998年王跃飞等［3］证明了定理3和定理4.

定理3设f（z）是开平面上的有穷级亚纯函数，k≥1是正整数，若f（z）满足f∈P2，则f≡常数.

定理4设F为区域D⊂ℂ内的亚纯函数族，k≥1是正整数，若对于任意f∈F，f∈P2，则F在D内正规.

同样，上述性质2也满足Bloch原理.

最近，常建明［4］将定理1中的限制条件“f（k）≠1”减弱为“f（k）-1有有限多个零点”，得到了定理5和定理6.

定理5设F为D内的非零亚纯函数族，k为正整数，如果对任意f∈F，满足f（k）-1至多有k个零点（不计重级），则F在D内正规.

定理6设F为D内的非零亚纯函数族，k为正整数，如果对任意f∈F，f（k）-1有至多k+1个零点（不计重级），设存在ε，满足0＜ε≤1，使得对任意f∈F，f（k）-1有k+1个可判别的单零点z1，z2，…，zk+1，并且满足

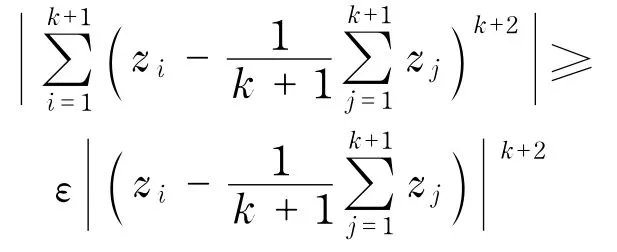
则F在D内正规.

本文从另一方面考虑函数的正规性，将定理1中的限制条件“f（z）≠0”减弱为“f的零点分布在一条直线上”，得到结果为：

定理7设F是定义在单位圆盘D上的亚纯函数族，若存在M≥0，使得对于任意f∈F，有

b.f的零点分布在一直线上；

c.f的极点重级m≥3；

d.f′（z）≠1，则F在区域D内是正规的.

2 主要例子

例1设fn（z）=n（ez-1），，易见fn（z）的零点为zk，n=2kπi，k∈ℤ，位于虚轴上，故zk，n∈D.因为f′n（z）=n ez，若，但当n充分大时，zm，n∉D.显然｛fn（z）｝在D上不正规.

注1例1说明定理7的条件是必要的.

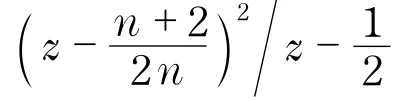
注2例2［5］说明定理7的条件“f的极点均为重级极点”是必要的.

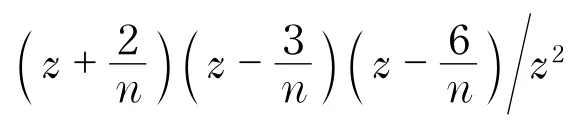
注2例2、例3说明定理7中的条件“f的极点重级≥3”是不能减弱的.

以上说明定理7中的条件“f的零点分布在一直线上”是必要的.

3 引 理

引理1［6］设F是单位圆盘上的亚纯函数，k≥1是正整数.F中每个函数的零点重级至少为k，且存在A≥1，使得对任意f∈F，当f（z）=0时，有.若F在z0处不正规，则对任意0≤ α≤k，必存在

a.点列zn→z0；

b.正数列ρn→0+；

引理2［7］设f为复平面上的非常数亚纯函数，b为非零复数，k为一正整数，则f或f（k）-b有零点；若f为超越亚纯函数，则f或f（k）-b有无穷多个零点.

引理4［8］若实函数f（x）满足如下条件：

a.f（x）在闭区间［a，b］上连续；

b.f（x）在开区间（a，b）内可导；

c.f（a）=f（b），则在（a，b）内至少存在一点ξ，使得f′（ξ）=0.

4 定理7的证明

证明若存在z0∈D，使得F在点z0处不正规.由引理1，存在点列zn∈D，zn→z0，函数列fn∈F以及正数列ρn→0+，使得在ℂ上

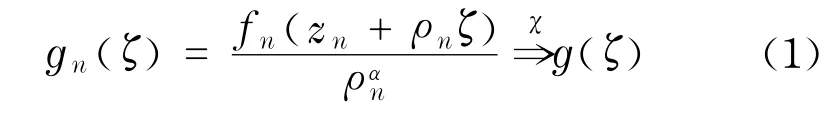
式中，g（ζ）为复平面ℂ上的非常值有穷级亚纯函数，并且g＃（ζ）≤g＃（0）=M+1.

所以断言：

a.g′（ζ）≠1；

b.g（ζ）的零点分布在同一直线上.

假设存在ζ0∈D使得g′（ζ0）=1，断言g′（ζ）≢1，否则g（ζ）=ζ-ζ1.因为，矛盾.因此由Hurwitz定理，存在ζn，ζn→ζ0，使得对于充分大的n，有g′（ζn）=1，即f′n（zn+ρnζn）=1，与f′（z）≠1相矛盾.故断言a成立.

下证断言b.不妨设g至少有3个不同的零点，设ζ1，ζ2，ζ3是g的任意3个相异的零点.由式（1）和Hurwitz定理知：对于δ＞0，存在点列ζn，i∈Dδ（ζi），i=1，2，3，当n充分大时有则fn（zn+ρnζn，i）=0.由条件知f的零点分布在一直线上，可得到tn为实常数，即

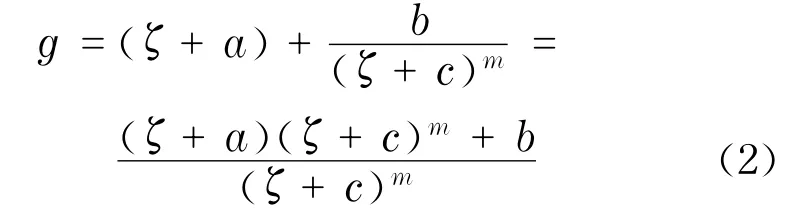
式中，a，b（≠0），c为有穷复数；m为正整数.

因为g的极点均为重级极点，由式（2）可得g至少有3个不同的零点.

设g的零点分布在直线L上：ξ=α+βζ，其中α，β∈ℂ，ζ∈（-∞，+∞）.令G（ζ）=g（α+βζ），那么G（ζ）的零点分布在实轴上.所以

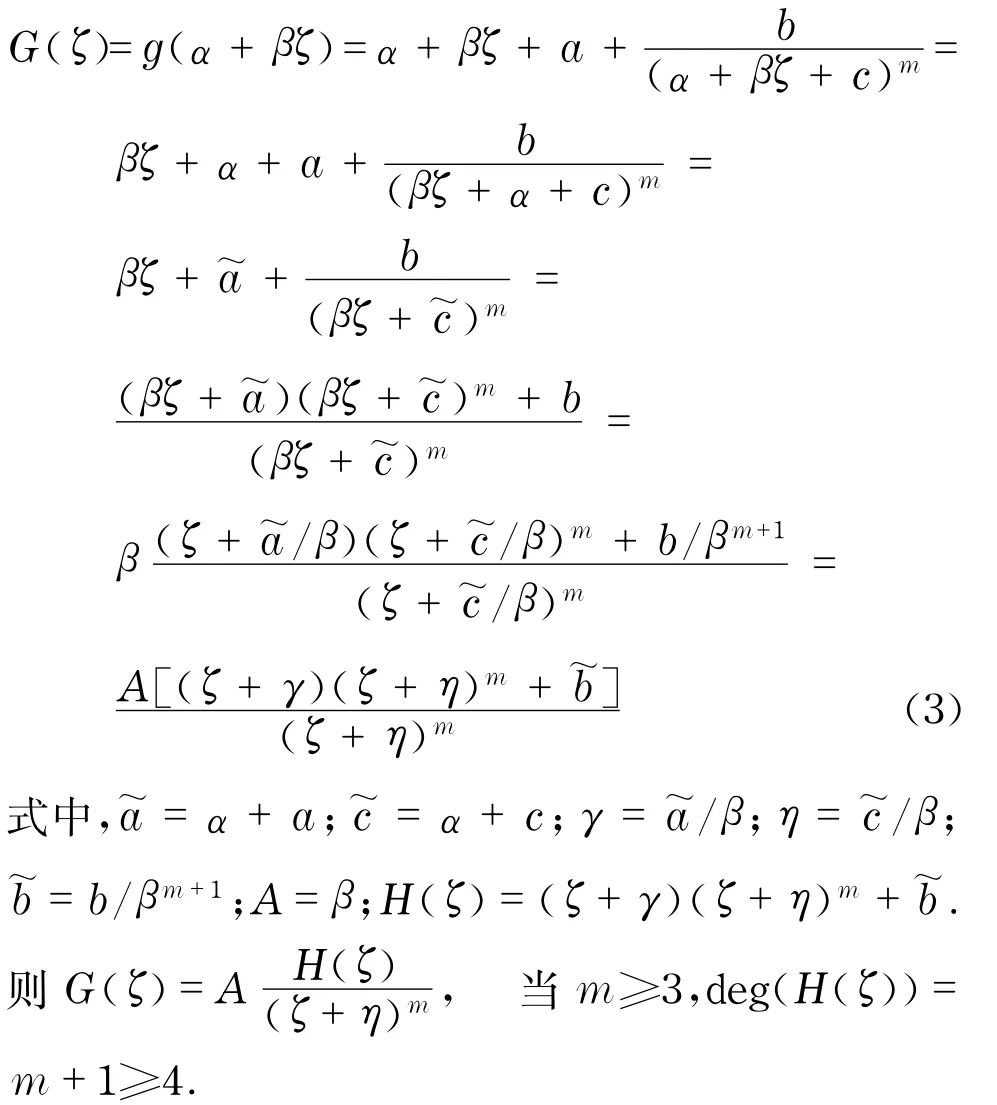
当deg（H（ζ））≥4，此时分两种情形进行讨论：

情形1H（ζ）仅有单级零点.

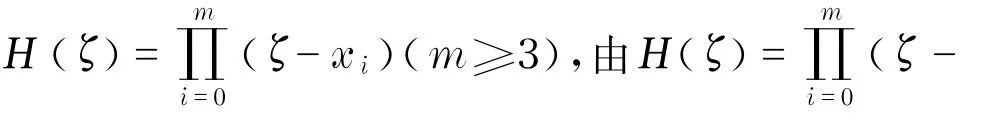
情形2H（ζ）有重级零点.

此时断言H（ζ）有重级零点，且仅有一个二重零点，可设ζ0是H（ζ）的重级零点，由

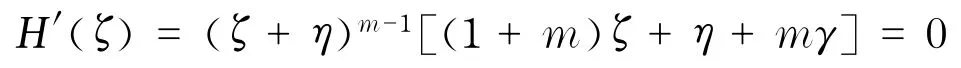
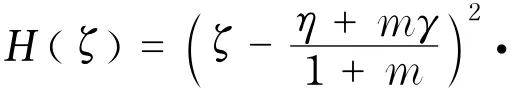
故F在D内正规.

［1］ Hayman W K.Meromorphic functions［M］.Oxford：Clarendon Press，1964.

［2］ Gu Y X.A normal criterion of meromorphic families［J］.Scientia Sinica Math，1979（1）：267-274.

［3］ Wang Y F，Fang M L.Picard values and normal families of meromerphic function with zeros［J］.Acta Math Sinica，1998，14（1）：17-26.

［4］ Chang J M.Normality and quasinormality of zero-free meromorphic functions［J］.Acta Math Sinica，2012，28（4）：707-716.

［5］ Nevo S，Pang X C，Zalcman L.Quasinormality and meromorphic functions with multiple zeros［J］.Anal Math，2007，101（1）：1-23.

［6］ Pang X C，Zalcman L.Normal families and shared values［J］.Bull London Math Soc，2002，32（3）：325 -331.

［7］ 顾永兴，庞学诚，方明亮.正规族理论及其应用［M］.北京：科学出版社，2007.

［8］ 华东师范大学数学系.数学分析［M］.北京：高等教育出版社，2001.

［9］ 孟耀霞，刘晓俊.涉及微分多项式的亚纯函数族正规定则［J］.上海理工大学学报，2013，35（1）：87-90.

（编辑：金 虹）

A Normal Criterion of Meromorphic Functions Whose Zeros Distribute on Some Straight Lines

TONGXiao-li， LIUXiao-jun
（College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

The normality of meromorphic functions whose zeros distribute on some straight lines was discussed and it is proved：let F be a family of meromorphic functions on a unit disk D，all of whose poles have multiplicity at least m，where m≥3 is an integer.If there exists M≥0，such that for each f∈F，all zeros of f distribute on a straight line，f′（z）≠1，z∈D andthen F is normal on D.

meromorphic functions；zeros；normal family

O 174.52

A

2013-05-20

国家自然科学基金资助项目（11371139）；数学天元专项基金资助项目（11226095）

童晓丽（1988-），女，硕士研究生.研究方向：复分析.E-mail：tongxiaoli5063261＠163.com

刘晓俊（1982-），男，副教授.研究方向：复分析.E-mail：xiaojunliu2007＠hotmail.com

1007-6735（2014）04-0362-04

10.13255／j.cnki.jusst.2014.04.011