欧氏Steiner最小树的Delaunay三角网混合智能求解方法

王家桢， 马 良， 张惠珍

（上海理工大学管理学院，上海 200093）

欧氏Steiner最小树的Delaunay三角网混合智能求解方法

王家桢， 马 良， 张惠珍

（上海理工大学管理学院，上海 200093）

欧氏Steiner最小树问题是组合优化中一个经典的NP难题，在许多实际问题中有着广泛的应用.由于使用普通智能算法求解较大规模问题时，极易陷入拓扑结构的局部最优，因此，基于Delaunay三角网技术并结合智能算法的有关思想，设计了一种改进的混合型智能求解方法，可大幅度提高算法在寻找更好拓扑结构上的有效性.算法在Matlab环境下编程实现，经大量STEINLIB中的标准数据实例测试和验证，获得了满意的效果，为求解较大规模的欧氏Steiner最小树问题提供了新的有效方法.

欧氏Steiner最小树；Delaunay三角网；多边形剖分；智能算法

Steiner树问题［1-2］是指连接给定点的最小树长问题，其最优解称为Steiner最小树（Steiner minimum tree，SMT）.该问题在实际中有着广泛的应用，如通信网络设计、印刷电路板设计、传输线布线等.

根据点和连线的空间属性，Steiner树问题可进一步细分为欧氏Steiner树（Euclidean Steiner tree，EST）问题和绝对值距离Steiner树（rectilinear Steiner tree，RST）问题（连线只有水平和垂直两种形式）.虽然已有精确算法可用于求解此类问题，但由于Steiner树问题已被证明是组合优化中的一个NP难题，现实而合理的办法往往是设计各种启发式算法以寻求问题的满意解.

本文基于计算几何中Delaunay三角网［3］的相关理论，利用智能算法，设计了一种改进型的混合智能求解方法.其特点在于从几何的角度入手，结合了智能算法的优点，大幅度提高了算法在寻找更好拓扑结构上的有效性.

1 欧氏Steiner最小树问题

给定原点集X（也称正则点集），欧氏Steiner树是指在欧氏平面上连接点集X中所有点的最短树.由于允许增加辅助点集S（s-点集），因此，Steiner最小树问题的本质就是寻求点集S，使得连接X∪S的生成树最小.

下面，先列出几条关于Steiner最小树的基本性质［4-6］：

性质1SMT上任何两条邻接边的夹角不小于120°.

性质2SMT上任何1个顶点的关联边不多于3条.

性质3SMT上与s-点相关联的边必定为3条，且这3条边中任意两边夹角为120°.

性质4设SMT的原点为n个，则s-点的数目小于等于（n-2）.

性质5假设由n个原点所围成的区域为凸包，则所有s-点都必定包含在凸包内.

性质6SMT中每个叶子都是原点，若能设法求出s-点的个数及其位置，就可用常规的最小生成树算法求得SMT，因此，问题的关键是寻找s-点.

2 Delaunay三角网

Delaunay三角网是Voronoi图（也称为Dirichlet图）的伴生图形，对它的研究是从对Voronoi图的研究开始的［7］.

Voronoi图定义假设V=｛v1，v2，…，vn｝，n≥3是欧氏平面上的一个点集，并且这些点不共线，4点不共圆，d（vi，vj）表示点vi，vj间的欧氏距离.设x为平面上的点，则区域V（i）=｛x∈E2｜d（x，vi）≤d（x，vj），j=1，2，…，n，j≠i｝称为Voronoi多边形，E2表示二维欧氏空间，各点的Voronoi多边形共同组成Voronoi图.

平面上的Voronoi图可以看作是点集V中的每个点作为生长核以相同的速率向外扩张，直到彼此相遇为止而在平面上形成的图形.除最外层的点形成开放的区域外，其余每个点都形成一个凸多边形.

Delaunay三角网定义有公共边的Voronoi多边形称为相邻的Voronoi多边形，连接所有相邻的Voronoi多边形的生长中心所形成的三角网称为Delaunay三角网.Delaunay三角网的外界是一个凸多边形，它由连接V中的凸集形成，通常称为凸壳.

Delaunay三角网具有两个非常重要的性质［8］：

a.空外接圆性质.在由点集V所形成的D-三角网中，其每个三角形的外接圆均不包含点集V中的其它任意点.

b.最大的最小角性质.在由点集V所能形成的三角网中，D-三角网中三角形的最小角度是最大的.

由于这两个性质，决定了Delaunay三角网具有极大的应用价值.同时，它也是二维平面三角网中唯一的、最好的.

3 普通智能算法求解Steiner树时的缺陷

图1（a）中是一株正则点个数n为5的欧氏Steiner最小树，且为满拓扑结构，使用的求解方法是遗传算法.图1（b）中是一株正则点个数n为15的欧氏Steiner最小树，使用的求解方法也是遗传算法.在图1（b）中有5个正则点和图1（a）中的5个正则点的位置完全相同.但非常遗憾的是，图1（b）中同样位置的5个点并没有构成满拓扑结构.这说明仅仅使用普通的智能算法求解欧氏Steiner最小树，拓扑结构极易陷入局部最优，而且当正则点个数较多时，一旦拓扑结构陷入了局部最优，智能算法几乎不可能跳出这样的局部最优.

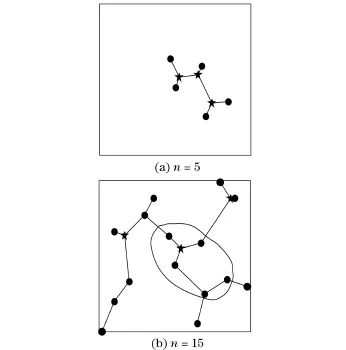
图1 智能算法缺陷示意图Fig.1 Shortcoming of basic intelligent algorithm

因此，针对上述问题，本文提出了一种与Delaunay剖分有关的混合智能方法来求解欧氏Steiner最小树，能够在很大程度上避免拓扑结构陷入局部最优.

4 算法描述及示例

欧氏Steiner最小树的Delaunay三角网混合智能算法具体步骤如下：

第一步对平面上给定的正则点构建Delaunay三角网，如图2所示.

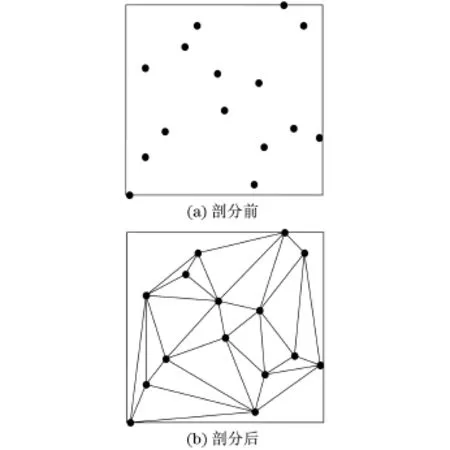
图2 Delaunay三角网示意图1Fig.2 Delaunay triangulation 1

这里不赘述构建Delaunay三角网的算法，该步骤在Matlab中操作起来比较简单，只需直接调用Delaunay函数即可.

第二步将这些三角形中3个内角均小于120°的三角形找出来，如图3所示.

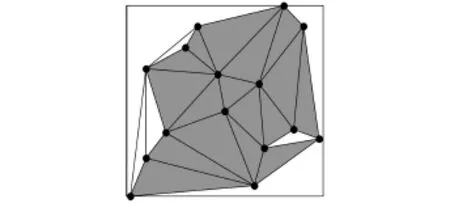
图3 Delaunay三角网示意图2Fig.3 Delaunay triangulation 2

第三步对3个内角均小于120°的三角形集合区域进行多边形剖分，如图4所示.

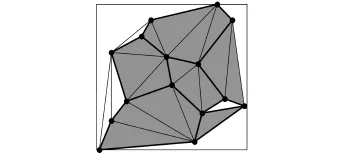
图4 Delaunay三角网示意图3Fig.4 Delaunay triangulation 3

多边形剖分遵循如下规则：

a.剖分必须沿着Delaunay三角网中三角形的边；

b.找出每个三角形的最长边，如果该最长边为某两个三角形的公共边，则将这两个三角形拼接在一起.

第四步利用智能算法对每一块区域所含的正则点逐块进行Steiner点的求解，如图5所示.

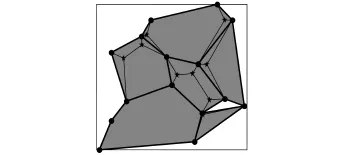
图5 满拓扑结构示意图Fig.5 Full topology structure

本环节所使用的智能算法为遗传算法.遗传算法［9］是一类借鉴生物进化思想的随机优化算法，通过选择、交叉、变异等操作产生下一代的解，并逐步淘汰掉适应度值较低的解，获得适应度值较高的解，经过多次这样的操作得出适应度最高的解.

a.染色体的产生

染色体的长度为2（n-2），其中，n为正则点的个数.每一个点的坐标产生方式为，随机选择一个三角形［10］，在这个三角形中生成一个随机点.用｛x1，y1，x2，y2，…，xn-2，yn-2｝这样的形式表示n-2个点的坐标，每两个数字表示一个点的坐标.

b.染色体的适应度

目标是生成树的长度最小化，因此适应度为该染色体中的Steiner点和正则点求得的最小生成树长度的倒数.

c.染色体的选择

利用随机遍历抽样法（stochastic universal sampling，简记SUS），此方法与轮盘赌选择法基本相似，是对轮盘赌选择法的一种改进，特点是只要进行一次轮盘旋转.其采用均匀分布且个数等于种群规模的旋转指针，等距离选择个体.其中第一个指针位置由［0，1／H］区间的均匀随机数决定，H代表旋转指针的个数.该方法提供了零偏差和最小个体扩展.

d.染色体的交叉

本文采用2-opt法进行交叉.需要注意的是，染色体断开的位置必须为偶数位置，目的是不把一个点的x坐标和y坐标割裂开来.

e.染色体的变异

随机删除染色体中的一个点的坐标，重新随机选择一个三角形，在其中生成一个随机点加入染色体中.

按上述步骤，对“第三步”剖分之后的每一个区域都使用一次遗传算法，得到每一块区域中的满拓扑结构.

第五步选择适当的满拓扑结构，构成最终解.

第四步中求得的所有满拓扑结构，并不能同时存在于最终的解中，例如本示例中图6的满拓扑结构1和满拓扑结构2不可能同时存在于最终解.

在满拓扑结构数量较小的情况下（如10以内的规模），可使用经典算法［11］，诸如分支定界法或回溯法等，精确地求得应选择哪些拓扑结构.但是在满拓扑结构数量较大的情况下，解空间的大小为2p，p为第四步中所求得的所有满拓扑结构个数，其时间复杂度为O（2p），用经典算法将在计算时间上达到难以容忍的程度.因此，这一步骤依然采用遗传算法进行求解.其中染色体的长度为满拓扑结构的个数，变量均为布尔型变量，0代表不选择该满拓扑结构，1代表选择该拓扑结构.

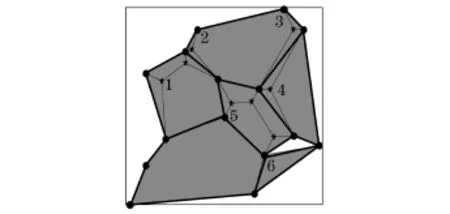
图6 示例满拓扑结构Fig.6 Full topology structure of the example

本示例求得的最终解如图7所示，入选的满拓扑结构有图6中的满拓扑结构1，3，5.

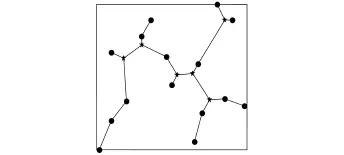
图7 示例结果Fig.7 Result of the example

将图1（b）和图7放在一起进行比较，如图8所示.

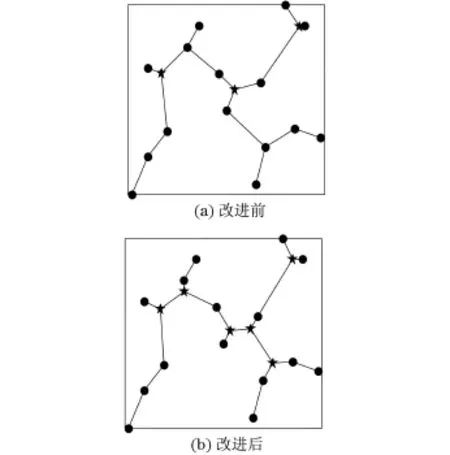
图8 改进效果对比Fig.8 Comparison of improvements

图8（a）具有3个满拓扑结构的正则点个数均为3，而图8（b）具有的3个满拓扑结构的正则点个数为3，4，5.很明显，图8（b）的拓扑结构要优于图8（a）的拓扑结构.

整个算法的时间复杂度主要来自有限次数的遗传算法，因此，该算法的时间复杂度等同于遗传算法的时间复杂度.整个算法的时间复杂度为O（MNn2）.其中，M为遗传代数，N为群体规模，n为正则点个数.

5 实例测试

为检验算法的有效性，上述算法用Matlab编程实现，并在国际通用的测试数据库STEINLIB中选取一系列的实例数据进行了测试，部分结果如下所示.

表1为一个正则点个数为16的实例，给出了16个正则点的坐标；表2是直接使用遗传算法所求得的s-点的坐标；表3是使用本文中改进后算法所求得的s-点的坐标.

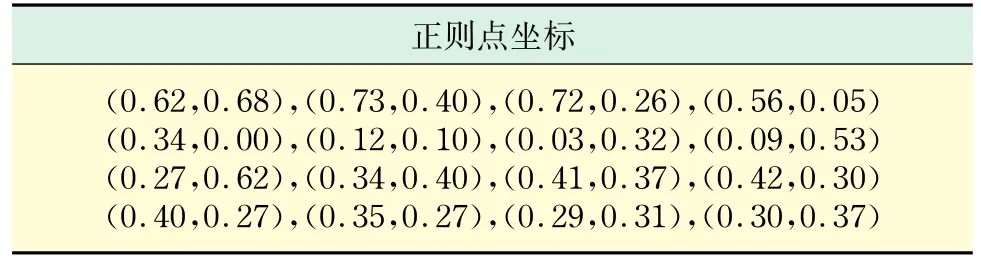
表1 正则点个数为16的实例数据Tab.1 Data for terminal vertices number of 16

表2 直接使用遗传算法求得的结果（n=16）Tab.2 Results of Steiner points by basic genetic algorithm（n=16）

正则点的最小生成树长度为2.400 4，直接使用遗传算法求得Steiner树长为2.349 0，使用本文上述算法求得Steiner树长为2.345 9.如图9所示，图9（a）为直接使用遗传算法，仅求得了3个Steiner点，且均为正则点个数为3的满拓扑结构；图9（b）为使用本文上述算法，求得了6个Steiner点，分别形成了正则点个数为3，4，5的3个满拓扑结构.

下面用一个规模更大的实例来进一步证明算法的有效性，表4为一个正则点个数为50的实例，给出了50个正则点的坐标.表5（见下页）是直接使用遗传算法所求得的s-点的坐标；表6（见下页）是使用本文中改进后算法所求得的s-点的坐标.

表3 使用本文算法求得的结果（n=16）Tab.3 Results of Steiner points by the modified algorithm（n=16）

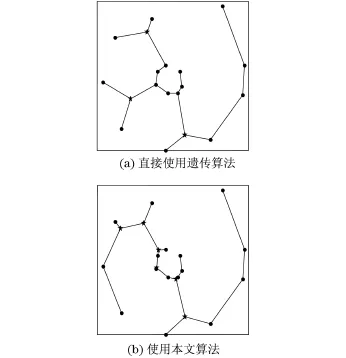
图9 改进效果对比（n=16）Fig.9 Comparison of improvements（n=16）

表4 正则点个数为50的实例数据Tab.4 Data for terminal vertices number of 50

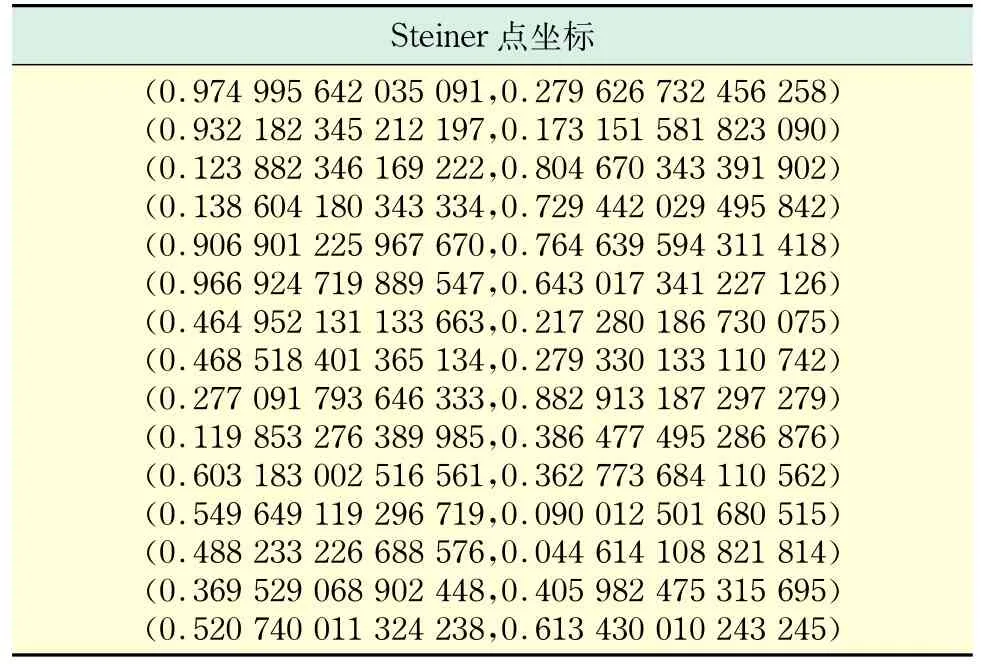
表6 使用本文算法求得的结果（n=50）Tab.6 Results of Steiner points by the modified algorithm（n=50）

正则点的最小生成树长度为5.143 1，直接使用遗传算法求得Steiner树长为5.046 3，使用本文上述算法求得Steiner树长为4.976 3.如图10所示，图10（a）为直接使用遗传算法，仅求得了5个Steiner点，且均为正则点个数为3的满拓扑结构；图10（b）为使用本文上述算法，求得了15个Steiner点，分别形成了5个正则点个数为3的满拓扑结构和5个正则点个数为4的满拓扑结构.

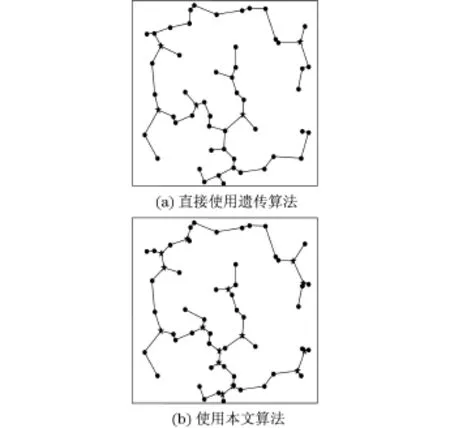
图10 改进效果对比（n=50）Fig.10 Comparison of improvements（n=50）

6 结束语

经大量实例测试和结果比较表明，本文给出的混合智能算法在拓扑结构上明显优于直接使用遗传算法，在求解Steiner最小树问题上，可起到很好的优化作用，且算法思路简单直观、易于实现，对现实中有关实际应用问题的解决提供了方便的求解手段和工具.

作为初步尝试，本文中的智能算法环节，仅选取了遗传算法作为基本方法，此环节可替换为其它的智能算法进行求解，亦可得到相应的改善和优化，有关工作将在后续研究中展开.

［1］ 马良，宁爱兵.高级运筹学［M］.北京：机械工业出版社，2008.

［2］ 马良，朱刚，宁爱兵.蚁群优化算法［M］.北京：科学出版社，2008.

［3］ Green P J，Sibson R.Computing Dirichlet tessellations in the plane［J］.The Computer Journal，1978，21（2）：168-173.

［4］ 越民义.最小网络——斯坦纳树问题［M］.上海：上海科学技术出版社，2006.

［5］ 丁雪枫，马良，丁雪松.基于模拟植物生长算法的构造通讯网络Steiner最优树方法［J］.上海理工大学学报，2010，32（1）：88-91.

［6］ 张瑾，单贵，马良.基于电势的最优加权Steiner树蚂蚁算法及其选址应用［J］.上海理工大学学报，2009，31（3）：283-285.

［7］ 武晓波，王世新，肖春生.Delaunay三角网的生成算法研究［J］.测绘学报，1999，28（1）：28-35.

［8］ 周培德.计算几何：算法设计与分析［M］.北京：清华大学出版社，2011.

［9］ 金慧敏.欧氏Steiner最小树问题的智能优化算法研究［D］.上海：上海理工大学，2005.

［10］ van Laarhoven J W，Ohlmann J W.A randomized Delaunay triangulation heuristic for the Euclidean Steiner tree problem in R-d［J］.Journal of Heuristics，2011，17（4）：353-372.

［11］ 王晓东.计算机算法设计与分析［M］.北京：电子工业出版社，2001.

（编辑：丁红艺）

Hybrid Intelligent Algorithm Based on Delaunay Triangulation for Euclidean Steiner Minimum Tree Problem

WANGJia-zhen， MA Liang， ZHANGHui-zhen
（Business School，University of Shanghai for Science and Technology，Shanghai 200093，China）

Euclidean Steiner minimum tree problem is a classical NP-hard problem in combination optimization，with a wide range of applications in many practical problems.Because of the easiness of getting stuck into local optimal topology by using general intelligent algorithms for large scale problems，a combination of Delaunay triangulation technique and intelligent algorithm wasintroduced to design a hybrid intelligent method，which can apparently improve the effectiveness of searching for better topology structures.The proposed algorithm was coded in Matlab，and was tested through series of standard instances from STEINLIB.The algorithm can obtain satisfied results and provide a new effective way to solve the problem of large scale Euclidean Steiner minimum tree.

Euclidean Steiner minimum tree；Delaunay triangulation；polygon decomposition；intelligent algorithm

TP 301.6

A

2013-07-20

上海市一流学科建设资助项目（S1201YLXK）；沪江基金项目（A14006）；上海市教委科研创新项目（14YZ090）；高校博士点专项科研基金联合资助项目（20123120120005）；上海高校青年教师培养资助计划（SLG12010）；上海理工大学国家级项目培育项目（13XGQ07）

王家桢（1988-），女，硕士研究生.研究方向：智能优化、系统工程.E-mail：ggggpeushmy＠foxmail.com

马 良（1964-），男，教授.研究方向：智能优化、系统工程.E-mail：maliang＠usst.edu.cn

1007-6735（2014）04-0351-06

10.13255／j.cnki.jusst.2014.04.009