考虑传播率和移出率变化的谣言传播规律研究

赵来军， 吴 盼

（1.上海交通大学中美物流研究院，上海 200030；2.上海交通大学安泰经济管理学院，上海 200052；3.上海大学管理学院，上海 200444）

考虑传播率和移出率变化的谣言传播规律研究

赵来军1，2， 吴 盼3

（1.上海交通大学中美物流研究院，上海 200030；2.上海交通大学安泰经济管理学院，上海 200052；3.上海大学管理学院，上海 200444）

经典的谣言传播模型的研究中，谣言传播率和移出率通常被视为常数，根据实际情况提出传播率和移出率变化的谣言传播模型，在均匀网络和无标度网络中分别研究了传播率和移出率随时间变化的谣言传播模型，建立相应的平均场方程，并在Matlab中进行数值分析.结果显示在传播率和移出率变化的谣言传播模型中，传播阈值依然存在，谣言最终的影响力较传播率和移出率不变的情况更为显著.此外，通过均匀网络与无标度网络谣言传播的对比分析发现，在传播率和移出率随时间变化的情况下，网络拓扑结构对谣言传播也有很大影响，并且均匀网络中谣言最终的影响力较无标度网络中谣言的最终影响力更为显著.

谣言传播模型；均匀网络；无标度网络；传播率函数；移出率函数

谣言是一种社会现象，更是一种典型的社会群体心理行为.随着新媒体时代的来临以及微博、博客、腾讯等SNS社交网站的流行，谣言传播的速度越来越快，谣言在人们生活中发挥的作用日益增强.人们可以利用谣言的传播达到某一种政治或者商业目的［1］.然而，很多谣言具有很强的破坏性，如不加以有效控制，会引起社会恐慌，造成巨大的经济损失［2］.2013年4月20日，四川雅安芦山县发生7.0级地震，就在政府和各方爱心人士积极抗震救灾之时，关于地震的谣言也在网络上四起.一位自称地震局内部人员的网民在百度贴吧发帖散布谣言，称“4月20日芦山7级只是前震，成都将于4月22日发生9.2级地震”，造成群众恐慌，被行政拘留.地震谣言对社会正常秩序和社会经济建设造成了相当大的危害.一场范围较大、持续时间较长的地震谣言风波造成的损失，有时不亚于一个破坏性地震.平息和抑制一次地震谣言与误传的发展，其内在的社会经济效益不亚于一次成功的地震预报［3］.因此，对于谣言传播规律的研究具有重要的现实意义.

谣言传播模型的研究始于1965年Daley和Kendall提出的DK模型［4］.在此模型中，人群被分为3类：知道谣言并传播的人、不知道谣言的人和知道谣言但不传播的人，分别称之为传播者、无知者和移出者.随着谣言传播研究的深入，Maki等［5］修改了DK模型，并提出了MK模型.基于以上这些模型，大批研究者开始研究谣言传播的规律［6-8］.与此同时，许多研究者开始关注社会网络的拓扑性质［9-11］.Zanette［12-13］首先将复杂网络理论应用于谣言传播的研究，在小世界网络上建立谣言传播模型，发现了谣言传播阈值的存在.Moreno等［14］研究了无标度网络中谣言传播的动力学机制，将计算机仿真和通过随机分析方法得出的结论进行了比较. Isham等［15］研究了一般网络上谣言传播最终的影响规模.Nekovee等［16］将遗忘机制引入谣言传播模型.赵来军等［17］根据对遗忘机制和记忆机制的研究，提出了一种新的谣言传播模型，即SIHR模型，他们同时也对均匀网络中谣言传播的动力学机制进行了研究.王筱莉等［18］在均匀网络上研究了考虑具有怀疑机制的谣言传播模型，并进行了仿真分析.

然而，实际上，一个无知者变成一个传播者的概率，即谣言传播率，以及一个传播者变成移出者的概率，即移出率，在谣言传播的过程中会随着事态的发展和人们的心理变化而变化.因此，本文考虑谣言传播率和移出率变化中的时间变量，假定传播率和移出率是随时间变化的函数.以前的研究将传播率和移出率视为常数［17-18］，本文将其视为随时间变化的函数，更符合实际情况中谣言的传播规律.

1 谣言传播规则

假设存在一个有总人口为N的混合均匀的社会网络，顶点代表社会中的个人，边代表两个人之间的连接，这样就可以得到一个无向图G=（V，E）. V是所有顶点的集合，E是所有边的集合.SIR模型中谣言传播的过程如图1所示，网络中的人群被分为3类：传播者S、无知者I、移出者R，分别表示知道谣言并传播谣言的人群（spreaders）、不知道谣言的人群（ignorants）、知道谣言但已失去传播能力或没有传播兴趣的人群（stiflers）.

图1 谣言传播过程Fig.1 Process of rumor spreading

SIR模型中谣言传播过程遵守以下规则：

a.当无知者I遇到传播者S时，无知者以λ（t）的概率变为传播者S，并进行下一轮传播.

b.当传播者S遇到另一个传播者S或者移出者R时，第一个传播者以α（t）的概率变为移出者R，α（t）称为移出率.

c.传播者S随时间推移忘记谣言或者忘记传播谣言以δ概率变成移出者R，δ称为谣言遗忘率.

在第一个规则中，个体以一定的概率接受谣言，这主要取决于谣言对特定个体的重要程度和可信程度.在第二个规则中，当个体与其他人交往时，已经知道是虚假谣言或陈旧谣言，就会失去传播谣言的兴趣，不再传播，由S态变为R态，其概率为α（t）.在第三个规则中，个体得知谣言后由于自身记忆力的衰退而忘记谣言，或者得知谣言后没有及时传播而忘记传播谣言，由S态变为R态，其概率为δ.谣言传播过程开始于一个或更多人被告知谣言，结束于人群中没有传播者.

企业基层思想政治工作者应在思想上引领、情感上交流、生活上关爱、素质上提升、成长上关怀，沟通思想，理顺情绪，化解矛盾，解决困难，做到全方位、多方式、全过程、创造性地开展思想政治工作，不断增强基层思想政治工作的实际效果。

2 谣言传播率函数和移出率函数的确定

本文中所研究的谣言为负面谣言，这类谣言如果不及时加以控制会引起群众恐慌，给社会带来重大损失，比如像雅安地震、H7N9、SARS、“抢盐潮”，诸如此类的非常规突发事件相关的虚假谣言.谣言传播过程中人们的心理变化如下：

a.谣言传播初期，许多人缺乏突发事件的危害程度、影响范围、持续时间等方面的知识，而这些信息会对个人的身体安全和财产安全产生重大影响.同时，政府的干预措施尚处于探索阶段.对于来历不明、没有详尽扎实事实支持的谣言（可能真实也可能虚假），大多数人难以或无法及时准确查证，许多人因而对谣言抱有一种宁可信其有不可信其无的心态.因此，谣言传播初期，传播率是快速上升的趋势，移出率是缓慢上升的趋势.

b.谣言传播中期，政府以及大量非官方媒体自发涌现对谣言进行制止.此时，公众对于突发事件掌握了更多信息，有了更好地了解，开始对谣言产生一定怀疑，传播率逐渐下降，移出率逐渐上升.

c.谣言传播后期，政府的干预措施逐渐成熟，采取例如揭露谣言、发布事实真相、组织官方媒体进行辟谣等措施.谣言止于信息公开，公众了解真相之后，即会停止传播谣言.因此，谣言传播率迅速下降，移出率迅速上升.

在非常规突发事件形势演化过程中，考虑以上因素，本文选择Weibull分布密度函数作为谣言的传播率.Weibull分布常应用于产品的可靠性和寿命实验的研究，传播率本身就是一个事件的寿命，应该服从普适的产品寿命分布.Weibull分布密度函数形式为其中x为随机变量；θ称为尺度参数；β称为形状参数.函数在时达到最大值.

从图2（a）可以看出，β＞1时，函数的形状会有一个上升下降的过程，β越大，函数峰值越大，到达峰值的时间越长.从图2（b）可以看出随着θ的减小，函数峰值越小，到达峰值的时间越长，函数越来越扁平.

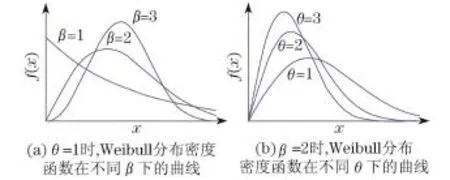
图2 Weibull分布密度函数曲线Fig.2 Curves of Weibull distribution density function

从图3可以看出，Logistic函数曲线刚开始缓慢上升，然后快速上升，最后缓慢上升直至饱和，这种变化趋势与本文所研究的移出率的变化趋势一致.从图3（a）可以发现ε越大，函数增长速度越快，曲线越陡峭.从图3（b）可以发现ρ越大，函数与y轴的交点值越小.

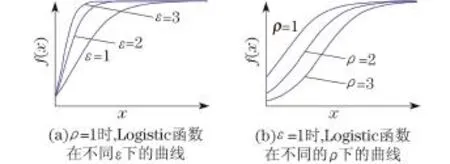
图3 Logistic函数曲线Fig.3 Curves of logistic function

3 均匀网络中考虑传播率和移出率变化的谣言传播模型

借鉴Nekovee等［16］对社交网络中谣言传播动力学机制的一般模型，建立谣言传播的平均场方程为

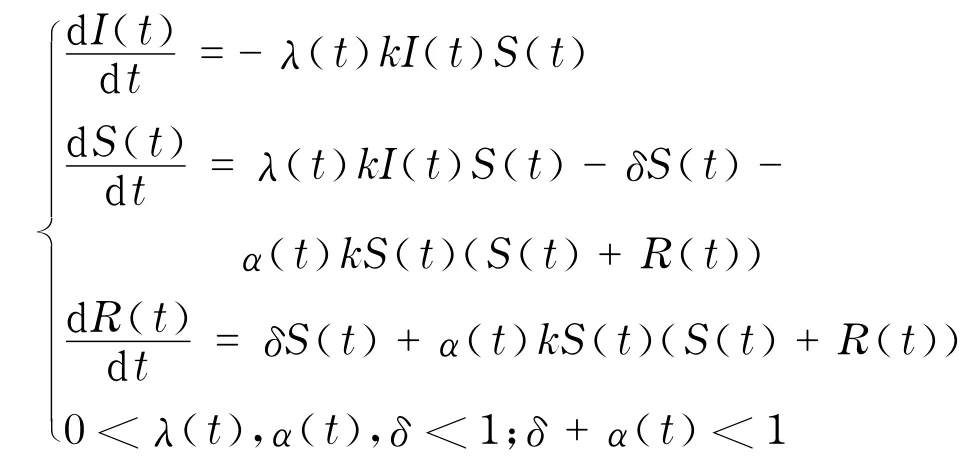
假设在总人口数为N的社会网络中，最开始时只有一个传播者，所以谣言传播的初始状态为

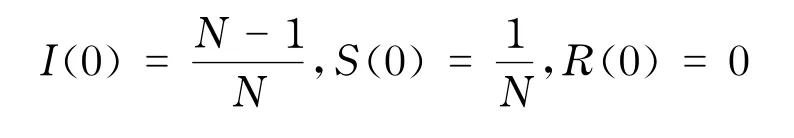
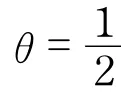
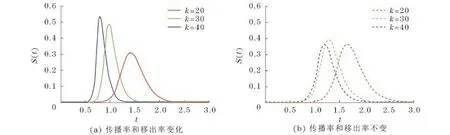
图4 均匀网络中传播者密度变化曲线Fig.4 Density of spreaders in homogenous network

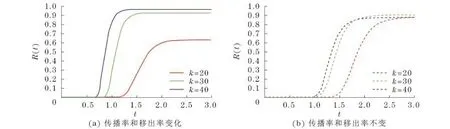
图5 均匀网络中移出者密度变化曲线Fig.5 Density of stiflers in homogenous network

从图4和图5可以看出，相较于传播率和移出率不变的谣言传播模型，传播率和移出率变化的谣言传播模型中的传播者峰值和移出者稳态值更大.随着网络平均度k的增大，传播者越快达到峰值，峰值越大，谣言传播过程结束得越快.随着网络平均度k的增加，移出者稳态值越大，谣言传播过程结束得越快.除此之外，在修改后的谣言传播模型中阈值依然存在，随着网络平均度k增大，阈值变小，谣言越容易传播开.

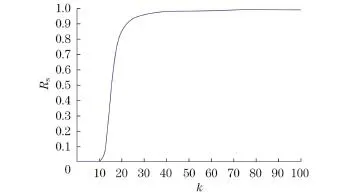
图6 移出者密度的稳态值RS随k增加的变化Fig.6 Change of the final size of rumor RSas k grows

传播率和移出率变化的谣言传播模型中移出者密度的稳态值RS随k增加的变化如图6所示.从中可以看出，传播率和移出率变化的谣言传播模型中，随着k增加，移出者稳态值增加，最终无限趋近于1.在k比较小的时候，k的增大对谣言传播最后的移出者规模影响显著；在k比较大的时候，谣言传播最后的移出者规模受其影响较小，趋于饱和.

4 无标度网络中考虑传播率和移出率变化的谣言传播规律研究

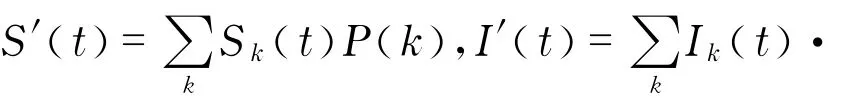
对无标度网络中修改后的谣言传播模型作数值分析，初始值和参数值与均匀网络中设置的相同.以BA无标度网络为例，其度分布为P（t）=2 m2k-3，其中m为网络最小度.考虑BA无标度网络中的SIR模型，N=104，m=15，因此〈k〉=30.运用Gephi生成相应的BA无标度网络，然后用有限差分法求解平均场方程.在接下来的计算中，从网络中随机抽取一个结点作为初始的传播者，抽取50次计算平均值.BA网络中传播者的密度曲线和移出者的密度曲线分别如图7（a）和图7（b）中红色细实线部分所示.传播者密度达到最高峰的时间以及移出者达到稳态值的时间分别记作tS，tR.传播率和移出率不变的SIR模型中传播者和移出者密度曲线分别如图7（a）和图7（b）中蓝色细虚线部分所示.其中，可以得出λ=0.34，α=0.28.同时，由于生成的BA网络平均度为30，选取均匀网络中平均度k为30的谣言传播来进行对比，其它参数与BA网络一样.均匀网络中传播率和移出率变化的SIR模型的传播者和移出者密度曲线分别如图7（a）和图7（b）中黑色粗实线部分所示，传播率和移出率不变的SIR模型的传播者和移出者密度曲线分别如图7（a）和图7（b）中绿色粗虚线部分所示.

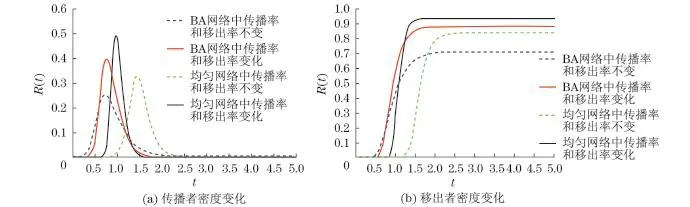
图7 BA网络和k=30的均匀网络中，传播者密度变化和移出者密度变化Fig.7 Density of spreaders and density of stiflers in the BA network and homogeneous network with k=30

从图7可以看出，与均匀网络中模型比较结果类似，传播率和移出率变化的谣言传播模型中传播者的峰值比传播率和移出率不变的要大，传播率和移出率变化的谣言传播模型中移出者的稳态值相对于传播率和移出率不变的也要大.这说明谣言传播率和移出率的改变对谣言传播有很大影响.同时，可以看出，在网络节点总数和平均度都相同的情况下，谣言在无标度网络中传播得更快，达到峰值的时间越早，谣言的最终传播规模也越小.这是由无标度网络的拓扑结构所决定，因为无标度网络中有一部分度很大的Hub节点，与它们相连的个体很多，这就导致这些Hub节点很容易得知谣言并将谣言传播给其它无知者，从而加速了谣言的传播过程.同理，这些Hub节点成为传播者或移出者后，也更容易使得与其相连的传播者变为移出者，从而加速了谣言传播的终止，使得谣言的最终规模更小.这说明，网络拓扑结构对谣言传播有很大影响，无标度网络较之于均匀网络能更好地抑制谣言的传播，减小谣言传播的影响.

5 结 论

本文通过对传播率和移出率函数的确定，对经典SIR模型进行修改，使之更符合实际谣言传播规律，在均匀网络和BA无标度网络中建立了相应的平均场方程，并进行数值分析，主要得出以下结论：

a.本文对均匀网络和无标度网络中的SIR模型都进行了数值分析.仿真结果显示传播率和移出率由常数变为随时间变化的函数，对谣言传播最终的规模大小和传播者峰值有很大影响.此外，传播率和移出率变化情况下，网络平均度对谣言传播也有很大影响.

b.仿真结果显示，传播率和移出率变化情况下，BA无标度网络中传播者密度峰值和移出者稳态值比均匀网络中的要小，谣言的最终影响力较小.

未来的研究中，由于各类的谣言事件有各自的传播规律，可以搜集实际的谣言事件数据，与理论模型的仿真结果进行拟合，得出相应的传播率和移出率函数参数，将其进行归类分析，得出针对不同类型谣言的控制策略，为政府更好地应对谣言提供决策支持.

［1］ Galam S.Modelling rumors：the no plane Pentagon French hoax case［J］.Physica A，2003，320：571-580.

［2］ Thomas S A.Lies，damn lies，and rumors：an analysis of collective efficacy，rumors，and fear in the wake of Katrina［J］.Sociological Spectrum：Mid-South Sociological Association，2007，27（6）：679-703.

［3］ 叶树明，沈士耕，严斌.地震谣言与误传的形成发展及其仰制传播对策［J］.地震学刊，1992（1）：34-39.

［4］ Daley D J，Kendall D G.Epidemics and rumors［J］. Nature，1964，204（4963）：1118.

［5］ Maki D，Thomson M.Mathematical models and applications：with emphasis on the social，life，and management sciences［M］.Englewood Cliff New Jersey：Prentice-Hall，1973.

［6］ Lefevre C，Picard P.Distribution of the final extent of a rumor process［J］.Applied Probability，1994，31（1）：244-249.

［7］ Pittel B.On a Daley-Kendall model of random rumors［J］.Applied Probability，1990，27（1）：14-27.

［8］ Kawachi K，Seki M，Yoshida H，et al.A rumor transmission model with various contact interactions［J］.Theor Biol，2008，253（1）：55-60.

［9］ Sudbury A.The proportion of the population never hearing arumour［J］.Applied Probability，1985，22（2）：443-446.

［10］ Chierichetti F，Lattanzi S，Panconesi A.Rumor spreading in social networks［J］.Theory Computer Science，2011，412（24）：2602-2610.

［11］ Doerr B，Fouz M，Friedrich T.Social networks spread rumors in sublogarithmic time［J］.Electronic Notes in Discrete Mathematics，2011，38：303-308.

［12］ Zanette DH.Critical behavior of propagation on smallworld networks［J］.Physical Review E，2001，64（5）：050901.

［13］ Zanette D H.Dynamics of rumor propagation on smallworld networks［J］.Physical Review E，2002，65（4）：041908.

［14］ Moreno Y，Nekovee M，Pacheco A F.Dynamics of rumor spreading in complex networks［J］.Physical Review E，2004，69（6）：066130.

［15］ Isham V，Harden S，Nekovee M.Stochastic epidemics and rumours on finite random networks［J］.Physica A，2010，389（3）：561-576.

［16］ Nekovee M，Moreno Y，Bianconi G，et al.Theory of rumor spreading in complex social networks［J］. Physca A，2007，374（1）：457-470.

［17］ Zhao L J，Wang Q，Cheng J J，et al.Rumor spreading model with consideration of forgetting mechanism：a case of online blogging LiveJournal［J］.Physica A，2011，390（13）：2619-2625.

［18］ 王筱莉，赵来军.社交网络中具有怀疑机制的谣言传播模型［J］.上海理工大学学报，2012，34（5）：424-428.

［19］ 朱陈平，张永梅，刘小廷.复杂网络稀疏性的统计物理研究综述［J］.上海理工大学报，2011，33（5）：425-431.

［20］ Pastor SR，Vespignani A.Evolution and structure of the internet：a statistical physics approach［M］. Cambridge：Cambridge University Press，2004.

（编辑：丁红艺）

Rumor Spreading Model with Variable Spreading and Removal Rate

ZHAOLai-jun1，2， Wu Pan3
（1.Sino-US Global Logistics Institute，Shanghai Jiaotong University，Shanghai 200030，China；
2.Antai College of Economics&Management，Shanghai Jiao Tong University，Shanghai 200052，China；
3.School of Management，Shanghai University，Shanghai 200444，China）

In the study of classical rumor spreading models，rumor spreading rate and removal rate are generally regarded as constants.Based on practical situations，a rumor spreading function and a removal rate function were proposed and a rumor spreading model with variable spreading rate and removal rate was studied in homogeneous and scale-free networks respectively.Mean-field equations were derived and numerical simulations were conducted in Matlab.The results show that in the rumor spreading model with variable spreading rate and removal rate，spreading threshold still exists and the final size of rumor spreading is larger than that in the rumor spreading model with constant spreading rate and removal rate.Furthermore，the comparison between rumor spreading processes in homogeneous network and heterogeneous network shows that network topological structure has a great impact on rumor spreading.The final size of rumor spreading in homogeneous network is larger than that in scale-free network.

rumor spreading model；homogeneous network；scale-free network；spreading rate function；removal rate function

C 939

A

2013-07-26

国家自然科学基金资助项目（90924030）；上海市教育委员会“曙光计划”资助项目（09SG38）

赵来军（1970-），男，教授.研究方向：安全管理、环境管理.E-mail：zhao_laijun＠163.com

1007-6735（2014）04-0345-06

10.13255／j.cnki.jusst.2014.04.008