单轮自平衡机器车的系统建模与最优控制

张团善，李文真

(西安工程大学电子信息学院，陕西西安710048)

单轮自平衡机器车的系统建模与最优控制

张团善，李文真

(西安工程大学电子信息学院，陕西西安710048)

针对高阶次、多变量、非线性、欠驱动的单轮自平衡车系统，提出了一种改进的最优控制算法.首先采用拉格朗日方程推导出力学模型，线性化后，得到系统的线性化方程，然后分别利用线性二次型最优控制算法和基于对称根轨迹的最优控制算法实现了单轮机器车的平衡控制和动态稳定.通过比较可以看出，基于对称根轨迹的最优控制算法较传统的最优控制算法有更好的稳定性和鲁棒性，仿真结果验证了力学模型的正确性和反馈线性化控制算法的有效性.

单轮自平衡机器车;拉格朗日方程;线性二次型;对称根轨迹

0 引言

单轮自平衡机器车作为一种新型的环保轻型代步工具以其体积小、功耗低、易于控制、适应地形变化能力强等特点，引起了许多业内研究者的兴趣.与其他类型的机器车相比，自平衡机器车最主要的特征是要在各种状态下保持机器车的姿态平衡［1］.单轮自平衡机器车的工作原理是通过收集外部采集的数据，设计平衡控制算法和反馈调节器使系统达到动态平衡.Salerno等人根据倒立摆特性，以机器车车体的旋转角度为变量得到了双轮自平衡机器车的动力学方程，并通过应用微分几何方法对系统各种控制器参数的状态变量进行了分析［2］;Vos等人针对典型的倒立摆自平衡机器车系统提出了一种自适应控制算法，实现了机器车的平衡控制，但没有实现其运动控制［3］;美国加州大学的学生研制出了一款带竖直飞轮和行走轮的自平衡机器车，利用极点配置算法实现了自身的平衡［4］;郭磊等人研究了一种带水平飞轮和运动配重机构的自平衡机器车，并根据线性理论MIMO方法设计了控制算法并进行了测试［5］.由于上述研究中的自平衡机器车结构复杂、非线性程度高，其良好的控制效果是建立在精确数学模型的基础上，用简单的PID调节器和状态反馈控制器难以实现机器车的动态平衡，需要设计复杂的非线性控制器，成本较高，故本文对只保留行走轮的单轮机器车进行了数学建模并使用传统的线性二次型最优控制算法和基于对称根轨迹的最优控制算法分别进行控制，实现了机器车的动态镇定和自平衡，同时兼顾了系统响应的快速性和稳定性.这样的设计简化了机器车的结构，增加了实用性，降低了控制难度并提高了线性控制算法的可靠性.仿真结果表明，在一定角度范围内，两种控制算法均能使系统达到稳定平衡状态，而SRL最优控制算法比传统的最优控制算法更有利于提高机器车的动态性能.

1 结构和动力学模型

1.1 结构特点及运动原理

单轮自平衡机器车的机械结构由车轮本体，内嵌的伺服电机和轮轴外侧的踏板组成;控制系统主要包括驱动器、传感器和控制板，如图1所示.

单轮自平衡机器车是个结构不稳定的系统，具有静不平衡性，必须采用动态平衡的策略，即让机器车在平衡点附近不停地运动进行调节.如果将人等效为直立的车体，则对单轮机器车的运动控制最终表现为对车轮位移和车体倾角的控制，即通过检测装置将倾角和位置信息反馈给执行电机，产生作用转矩，对系统的状态进行实时的反馈调节，使机器车按照给定的速度运动，同时保证车体的转角为零.

1.2 模型建立及参数说明

将直立的人等效为直立的车体，当人站立在轮轴两侧的踏板上时，整个系统的重心位于轮子上方，而车轮只有一个支点与地面接触，如图2所示.建立模型前，假设以下条件：(1)车轮、车体均为刚体;(2)不考虑机器车和车体所受的外界干扰力;(3)不考虑车体与轮子之间的滑动摩擦力; (4)车轮与地面不打滑.建立如图3所示直角坐标系，规定机器车的前进方向为x轴正方向，与y轴垂直，轮子的轴线方向为z轴方向.

设车轮质量为m，车体质量为M，车轮半径为R，轮心到车体质心的距离为L，车轮绕z轴的转角为θR，车体绕y轴的转角为θP，电机对车轮的转矩为C，车轮的位移为xR，车体对Y轴的转动惯量为Jpθ，车轮对Z轴的转动惯量为JR.

图1 单轮自平衡机器车实物照片

图2 单轮机器车结构图

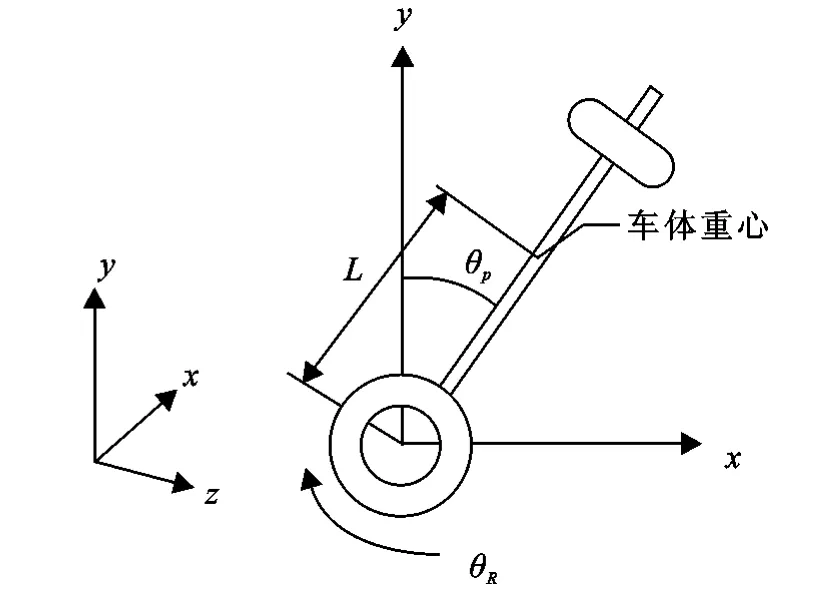
图3 系统坐标系和几何参数含义

自平衡机器车有车轮位移、车体转角两个自由度，但只有一个控制输入(电机的作用转矩)，是典型的欠驱动系统.严格地讲，它和倒立摆一样，是一种欠驱动连杆系统，其中车轮是主动关节，车体属于被动执行机构，车轮位移与车体转角两变量之间存在耦合关系［6］.由于欠驱动连杆系统具有多变量、强耦合的特性，用牛顿力学的分析方法为其建立准确的数学模型将十分复杂，因此本文选用拉格朗日方程从能量学的角度对系统进行动力学建模.其中数学表达式为

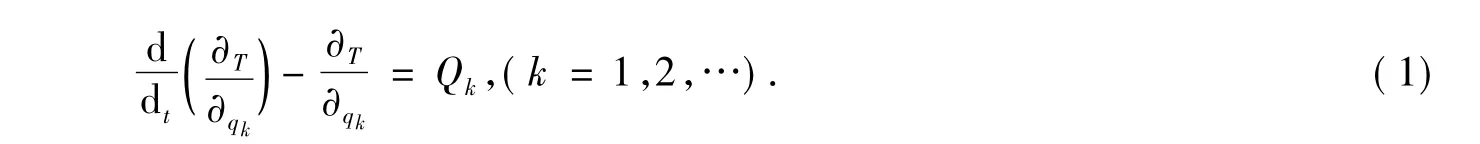
式中T为系统的总动能，q为系统的广义坐标，Q为系统的广义力.

选取车轮转角和车体转角作为系统的运动状态变量，由这两个相互独立的状态变量可以惟一确定系统的位置，在此坐标系下，车轮转角对应的广义力等于电机对车轮的作用转矩，而车体转角对应的广义力等于车体重力与电机对车体的作用转矩，即

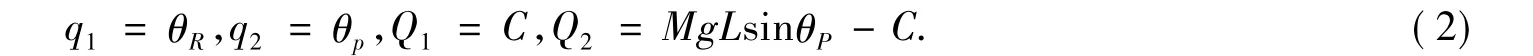
系统的动能包括车轮的平动动能T1，车轮绕z轴的转动动能T2，车体的平动动能T3，车体绕过其质心且平行于z轴的转动动能T4，表达式如下

系统总动能为

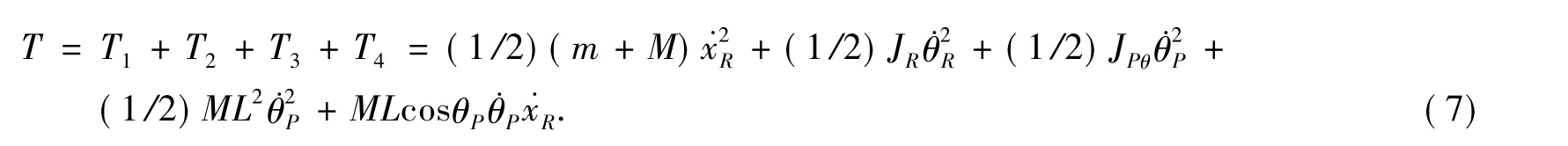
为简化模型和局部线性化，对车体的转角做如下约束：在平衡点附近时令sinθp≈θp，cosθp≈1.将式(2)～(7)代入式(1)，可得以下线性方程组：

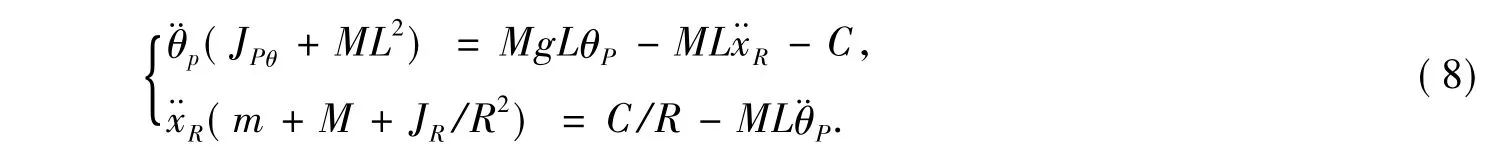
整理式(8)，并代入系统参数可得到线性化的数学模型：

系统参数见表1(注：为了方便后期系统模型的制作与硬件调试，在建立参考模型时对整个系统进行了适当的缩小).

表1 系统参数

由系统的状态方程知，该系统是单输入多输出的欠驱动系统，但各个状态变量之间存在耦合，结合能量传递的思想，对不可驱动状态变量的控制可以通过对可驱动状态变量的控制来间接达到.因此，可以通过状态反馈实现对整个欠驱动系统的实时控制.

用拉格朗日方程建立模型的方法是从总体能量的角度考虑，故在模型建立的过程中可以忽略系统内部之间的作用力，通过选择不同的状态量和输出量达到不同的控制效果［7］，为了达到全面的控制效果，将系统的4个状态量均选为输出量，对系统实施全反馈控制.

结合能控性判别矩阵M=［B，AB，A2B，A3B］，经MATLAB计算得rank(M)=4，系统能控;同理，由系统能观性矩阵N=［C，CA，CA2，CA3］T可知，rank(N)=4，系统能观.

1.3 系统的稳定性分析

线性定常系统稳定的充要条件是其全部特征根均具有负实部［8］.因本文将单轮自平衡机器车近似为不随时间改变的线性系统，故可以通过线性定常系统的稳定性判据对系统进行判稳.

由特征值方程

可得系统的特征值为

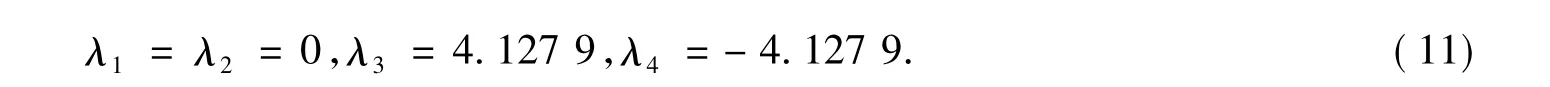
从式(11)可以看出，系统有一个正特征值和两个零特征值，不满足劳斯稳定的必要条件，而且无论怎样调节系统的参数，都无法使之达到稳定的状态.反馈控制可以将闭环系统的极点配置在根平面上所期望的位置，使系统达到稳定状态，而任意配置极点的充要条件是系统能控能观［9］，这是上文判断能控能观性的意义所在.

图4是系统的开环阶跃响应，可以看出此时系统是不稳定的，这与上述稳定性分析的结果一致.

图44 个状态量的开环阶跃响应

2 系统控制器设计

2.1 LQR控制器设计

单轮机器车的平衡问题，是一个状态正定问题，目标是在行走时使车体保持直立的状态，由于单轮自平衡机器车是一个高阶系统，使用传统的PI调节器进行控制时位移和速度曲线的振荡较为严重，甚至出现系统失控的现象［10］.因此本文选择了线性最优控制理论来设计反馈控制算法，目标是在车体的倾角为零，位移和速度稳定在固定值的基础上，使系统的性能指标达到极小.根据无限时间的线性二次型最优状态调节器理论，当tf趋于无穷时，最优控制问题等效为寻找一个控制量u(t)=-kx(t)使得以下的二次型性能指标［11］达到极小值：

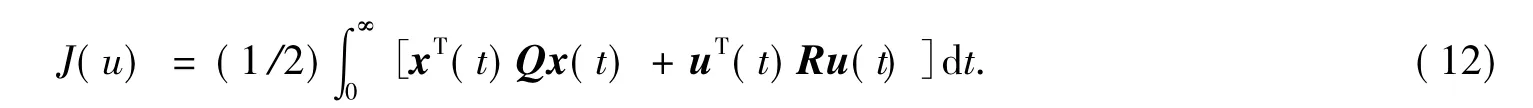
式中x(t)为n维状态向量;u(t)为r维控制向量;Q矩阵是半正定m×m实对称矩阵;R是正定r×r实对称矩阵.

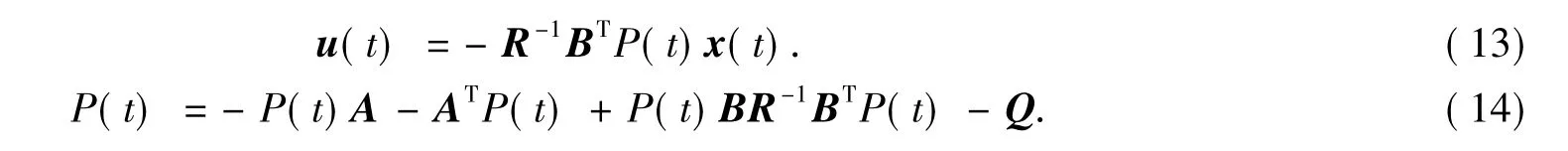
其中P(t)可由方程(14)解出;u(t)为主动控制力方程.

求解式(14)需要给定两个重要参数，即Q矩阵和R矩阵.其中，Q矩阵代表状态向量的权重，R矩阵则代表控制量的权重，它们分别表示系统运动过程中动态跟踪误差的总度量和能量消耗的总度量.在平衡控制中稳定的动态性能是首要要求，低能耗是次要要求，故取R=1.Q矩阵中的非零元素代表在控制过程中系统对各个状态的误差要求，经反复测试，并参照控制中车体和轮子的位移大小，取Q=［1000 0 0 0;0 0 0 0;0 0 100 0;0 0 0 0］.

因为Riccati方程较为复杂难解，在得知Q、R矩阵的前提下可以利用MATLAB函数库中的lqr函数帮助求解式(13)和式(14)，得到系统的最优反馈增益矩阵

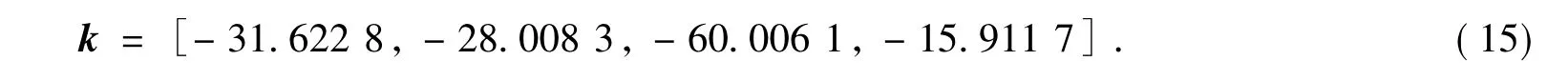
LQR控制方法的simulink仿真模型如图5所示.经MATLAB仿真可得，在此控制方案下，系统4个状态量的阶跃响应如图6所示.由图6可以看出，给系统加入阶跃扰动时，系统能够较快地达到平衡状态，在此过程中位移的超调量约为30mm，倾角的超调量约为0.02rad，调节时间约为2s，稳态误差、上升时间也符合稳态要求.在此基础上，如果再增加Q矩阵中的某些元素，系统的动态性能响应还会有所改善，但控制量也会上升，在保证控制量足够小，兼顾其他动态响应指标的基础上，此时的系统性能已经能够满足要求.

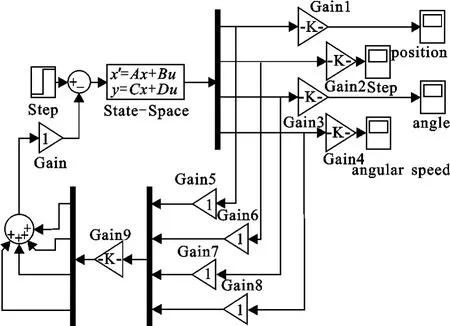
图5 LQR仿真模型

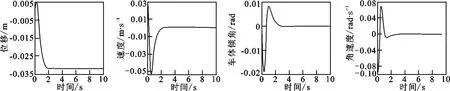
图6 LQR控制下的系统仿真曲线

2.2 基于SRL的最优控制器设计

针对高阶次的系统，采用极点配置实现状态反馈的方法虽简单直观，但对期望极点位置的选择十分复杂，且无法确定期望极点的最优或较优，传统的LQR调节器虽通过确定加权矩阵的方法找到了最优的反馈增益矩阵，但确定加权矩阵Q和R的普遍方法是仿真试凑法，即先初步选取Q和R，如果符合要求就求出最优增益矩阵K.进行仿真实验，如果不符合须重新选取，直至符合系统的性能指标要求［12］，矩阵中因数的选择主要依赖于设计者的经验和调试，具有较大的盲目性.因此，本文根据对称根轨迹(SRL)的原理，把最优控制和极点配置的思想结合起来，选择了一个新的性能指标函数，用于得到期望的最优闭环极点，即，将传统的最优控制规律简化描述成如下的性能指标［13］

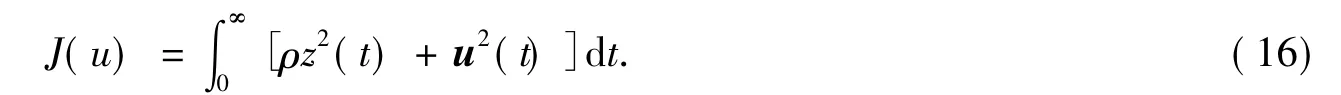
对如下的系统能够最小，即

其中式(16)中的z2(t)为系统跟踪误差的权值，u2(t)为系统控制量的权值，ρ是加权系数又称根轨迹参数，用于权衡跟踪误差对于控制量的相对损耗.以下是对称根轨迹方程的解：

使J(u)最小化的控制规律由线性反馈u=-kx得到，这里k的最优值即以上对称根轨迹方程中稳定根位置上的k值.可以看出s和-s对式(18)的影响是相同的，对于式(18)的任意根s0，必将对应一个根-s0，因此称所得的根轨迹为对称根轨迹，对称的含义是此根轨迹关于原点对称.最优主导极点可以由SRL中参数ρ所对应的稳定极点得到，在此根轨迹下选取的稳定极点具有使性能指标式(16)极小的特点，文献［13-14］给出了SRL的产生过程和SRL上的稳定极点使性能指标式(16)极小的证明，在此不做阐述.

利用SRL设计最优控制器的过程是先选定矩阵H(H决定了系统的跟踪误差，需保持一个很小的值)，再根据式(18)画出SRL曲线，在曲线中选取适当的ρ值(它平衡了跟踪误差和控制量对系统的重要性)，并找出与之对应的极点，然后将这些极点用于极点配置的运算中，得到反馈增益K，对系统进行反馈控制.

在上述理论基础上结合系统对位置和角度的输入要求，取跟踪误差矩阵H为

代入式(17)可得系统跟踪输出与控制输入的传递函数

图7给出了由式(18)所得的对称根轨迹.

由于最优的闭环极点一定是稳定的，所以选择左半S平面上的极点.经MATLAB计算得：当ρ=1时，对应的极点为-4.14+0.24i，-4.14-0.24i，选择这两个极点作为主导极点，在此基础上，取-20+i和-20-i作为辅助极点，它们位于主导极点的左侧，距离虚轴的距离是主导极点的5倍，对系统的影响较小.故期望的闭环极点为［-20+i，-20-i，-4.14+0.24i，-4.14-0.24i］.

结合MATLAB的状态反馈函数：K=acker(A，B，P)得出反馈增益矩阵，其中，P为各个期望极点的值，即

将新的最优反馈矩阵K代入图5的Simulink仿真模型中，可以得出在此控制方案下，4个状态量的阶跃响应，SRL控制下的系统仿真曲线如图8所示.

由图8可以看出，改进后系统的调节时间大约是0.5s，比传统的LQR控制器的调节时间缩短了1.5s，响应速度变快，超调量也明显减小，动态稳定性有所提高.结果表明，参数ρ的选择是合理的.

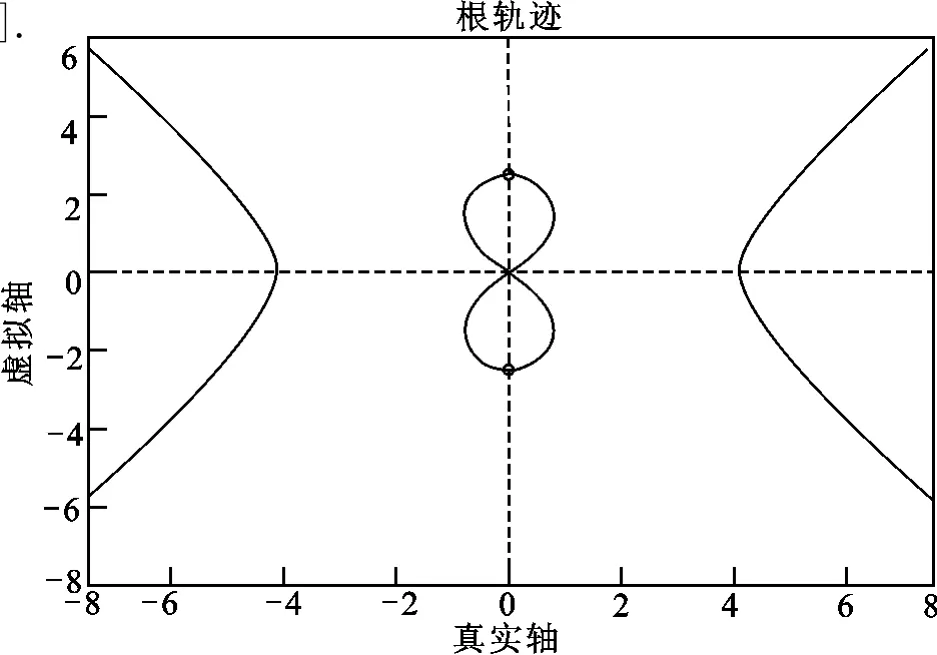
图7 机器车系统的对称根轨迹

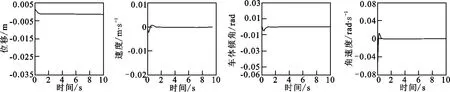
图8 SRL控制下的系统仿真曲线

在选择期望极点时，应该考虑系统的动态性能和闭环极点对于控制量的影响，否则容易导致控制量过高.传统的最优控制算法虽使控制量达到了一个较小的值，却无法建立起性能指标与系统误差之间的联系，并且确定权矩阵是很困难的，必须经过多次实验找到合适的加权矩阵.而基于参数的SRL最优控制方法在一定程度上抑制了选择加权矩阵时对系统的主观影响，使控制方法更易把握，并用参数ρ平衡了输入量与跟踪误差对系统的影响，实现了最优和稳定的统一.

参数ρ的选取有一定的限制条件.当ρ→0时，被控对象处于“高代价控制”情况，不利于控制能量的利用，很低的控制使用在系统的跟踪输出量z上产生了很大的误差;而当ρ→∞时，被控对象处于“廉价控制”的情况，在这种情况下，反馈增益矩阵K是无界的，同样不利于实际系统的控制.因此，本文在选取参数ρ时全面考虑了系统根的位置、时间响应、反馈增益、阻尼比等因素，并进行了大量的实验，最终达到了控制量、跟踪误差与控制效果之间的动态平衡.

综上所述，SRL法既得到了理想的最优闭环极点进而保证了良好的控制性能，又能在系统误差与控制量之间达到动态平衡，综合了最优控制理论和反馈控制方案，达到了控制量与控制效果的统一.较之传统的LQR控制，对称根轨迹法控制的超调量小、控制方法简单、响应速度快，在实际中具有更高的应用价值.

3 结束语

单轮自平衡机器车是非线性、欠驱动、高阶次系统的典型代表之一，本文在局部线性化的基础上用全状态反馈实现了对欠驱动状态变量的间接控制，并采取构造不同的线性二次型最优性能指标函数的方法，设计了平衡控制算法.仿真结果表明，基于LQR的最优控制方法和基于SRL的最优控制方法都可以使单轮自平衡机器车系统达到稳定状态，而基于SRL的最优控制方法既消除了LQR控制算法中选取Q，R矩阵的不确定性，又利用参数ρ的选择，找出了系统响应与期望极点的位置、时间响应及反馈增益之间的关系，控制方法简单、响应速度快、超调量小，因此在实际中具有更高的应用价值.

［1］阮晓刚.两轮自平衡机器人的研究与设计［M］.北京：科学出版社，2012：10-17.

［2］A SALERNOA，J Nonlinear.On the nonlinear controllability of a quasiholonomic mobile robot［C］//Proc of IEEE ICRA，Taiwan，2003：3379-3384.

［3］VOS D W，Von FLOTOW A H.Dynamics and nonlinear adaptive control of an autonomous unicycle：Theory and experiment［C］.IEEE，USA：1990：182-187.

［4］常文超.自平衡独轮机器人控制系统的研究［D］.河北：河北科技大学，2012.

［5］郭磊.单轮车机器人的动力学建模与非线性控制［J］.系统仿真学报，2009，21(9)：2730-2733.

［6］孙宁.一类欠驱动系统的控制方法综述［J］.智能系统学报，2011，6(3)：200-203.

［7］阮晓刚.两轮自平衡机器人动力学建模及其平衡控制［J］.计算机应用研究，2009，26(1)：99-103.

［8］刘豹.现代控制理论［M］.北京：机械工业出版社，2001：157-177.

［9］郑大钟.线性系统理论［M］.北京：清华大学出版社，2002：281-283.

［10］FAIZAN F，FARID F，REHAN M.Implementation of discrete PID on inverted pendulum［J］.Education Technology and Computer，2010，70(11)：48-51.

［11］吴受章.应用最优控制［M］.西安：西安交通大学出版社，1987：10-20.

［12］POWELL J David.动态系统的反馈控制［M］.朱齐丹，译.北京：电子工业出版社，2004：138-190.

［13］T Kailath.Linear systems［M］.Englewood Cliffs：Prentice Hall，1980：158-258.

［14］ROB Hoogendijk，A J Den Hamer，GEORGO Angelis，et al.Frequency response data based optimal control using the data based symmetric root Locus［C］//2010 IEEE International Conference on Control Applications，Yokohama，Japan，2010： 1010-1015.

System modeling and optimal control for the self-balancing unicycle

ZHANG Tuan-shan，LI Wen-zhen

(School of Electronics and Information，Xi'an Polytechnic University，Xi'an 710048，China)

An improved optimal approach is proposed for the high order，multivariate，typical nonlinear underactuated unicycle.The dynamical model is firstly established based on Lagrangian formulation.The tangent linearization of the model at its equilibrium yields to the linearization nominal model.Then respectively using LQR optimal algorithm and SRL optimal control algorithm to achieve dynamic balancing and motion control of the unicycle.By the simulation comparisons，SRL optimal control algorithm has a better anti-jamming and robustness than LQR optimal control algorithm.Computer simulation verifies the validity of the dynamic model，the effect of the controller is testified by simulation experiments.

self-balancing unicycle;Lagrangian equations;linear quadratic regulator(LQR);symmetrical root locus(SRL)

TP 242

A

1674-649X(2014)01-0077-07

Lagrange乘子进行求解，可以得到

编辑：武晖;校对：孟超

2013-08-04

张团善(1971-)，男，湖北省随州市人，西安工程大学副教授，硕士生导师.E-mail：zz102@sina.com