三维人体的点云获取与点云重建

李鹏飞，侯毅星，景军锋，2

(1.西安工程大学电子信息学院，陕西西安710048;2.陕西省纺织印染自动化工程技术研究中心，陕西西安710048)

三维人体的点云获取与点云重建

李鹏飞1，侯毅星1，景军锋1，2

(1.西安工程大学电子信息学院，陕西西安710048;2.陕西省纺织印染自动化工程技术研究中心，陕西西安710048)

针对三维人体重建中人体曲面复杂，点云庞大的问题，提出一种基于三维Voronoi图，并利用Delaunay三角剖分性质的Crust算法进行人体三维重建.采用三角测量原理计算三维坐标，散乱的点云构成Voronoi图，Delaunay三角剖分Voronoi图得到原始模型.利用Xjtuom三维面扫描仪测量人体点云，进而采集到了49幅不同角度和高度的图片，并用自带软件完成了配准.通过Matlab平台完成点云读取，点云精简和基于Crust算法的三维重建.实验表明，该算法可以保证曲面重建的拓扑正确性和收敛性.该三维重建系统能够实现人体庞大点云的三角剖分与人体复杂自由曲面的重建，并得到了360°无缝隙的人体重建模型.

三角测量;点云精简;Crust算法;三维重建

激光测量具有非接触、速度快、效率高等特点，成为近年来应用最广泛的实物数字化方法.但是激光测量产生的人体点云规模巨大，远远超过了刻画人体细节所需的密度.人体三维重建是从实物数字化所得的散乱点云中重构出忠实于原始人体曲面的三角形网格的过程，为人体尺寸测量［1］、三维试衣系统［2］的研究提供了基础.

三维重建的研究始于Lerensen［3］提出的Marching cube方法，该方法可以实现均匀密度表面的重建.Hoppe［4］等在此基础上通过计算点云的微切平面来估算点到真实曲面的有向距离，用隐曲面的方法构建三维模型，这一方法的难点在于近似模型的选择.外扩方法［5-6］作为一枝独秀，成为近期三维重建的热点，通过逐步向网格曲面边界边添加三角形来实现三角剖分，其结果是已三角化区域和未三角化区域的交界不断向外展，直到所有点都被网格曲面覆盖.该方法的难点是如何将新三角形添加到已三角化的区域中.1998年著名的SIGGRAPH会议上，Nina［7］等人提出了基于Voronoi图的Crust算法，成为近年来三维重建的热点［8］，对于高密度的点云可以保证拓扑正确性与对原始曲面的收敛性，该算法的不足在于只能对十万级以下点云有良好的重建效果.由于Crust算法有很强的理论保证，如果将Crust算法用在人体三维重建上，能够保证生成的网格曲面与人体曲面保持拓扑一致性;Crust算法不需要计算距离函数，可以自动获取参数，应用比较便捷;Crust算法允许采样密度是不均匀的;这种算法的优点还在于输出的离散曲面在细节区域具有密集点，而在无特征的区域具有稀疏点，符合人体曲面建模的特点.

综上，本文在基于三维重建的现状以及人体自由曲面的特性的基础上，先对人体进行了360°测量，然后做出了适合人体的数据精简，使之适合于Crust算法，最后用Crust算法完成人体三维重建.

1 数学基础

1.1 三角测量原理

将CCD相机采集到的图像还原出人体的三维坐标时，需要用到三角测量原理(图1).以XYZ为参考坐标系，其中三维光学面扫描系统投影仪和CCD相机的光心OP点与OC连线平行于参考平面R，即XY平面，Z轴与投影仪光轴方向平行，表示高度信息.当投影射线OPA经被测物上一点H时，成像于CCD相机上的像素点E(i，j).假设没有被测物体时，投影射线OPB经参考面上一点B与投影射线OPA成像于一点.由于OCOP与XY平面平行，则三角形AHB相似于三角形OPHOC，进而得到式(1).由式(1)可推出式(2)，其中，ZH表示H在Z轴方向分量L为OCOP到参考平面的距离.若H为任一空间点，由于三角形AHH′与三角形AOPO相似，该点的XH，XP坐标可通过ZH得到，式(3)为其XH坐标求法，同理可得YH坐标.

图1 三角测量原理

1.2 Voronoi图

Voronoi图是将散乱的点云连接成曲面的常用手段.Voronoi图，又叫泰森多边形，是由一组连接两邻点直线的垂直平分线组成的连续多边形组成.假设P={P1，P2，…，Pn}是欧几里德平面上的一个点集，并且这些点不共线，四点不共圆.用d(Pi，Pj)表示Pi，Pj间的欧几里德距离.设p为平面上的点，则区域Vi={p∈E2|d(P，Pi)≤d(P，Pj)，j=1，2，…，n，j≠i.}称为点p的Voronoi多边形.图2是20个点集的Voronoi图.图2中虚线表示Voronoi图，实线表示Delaunay.

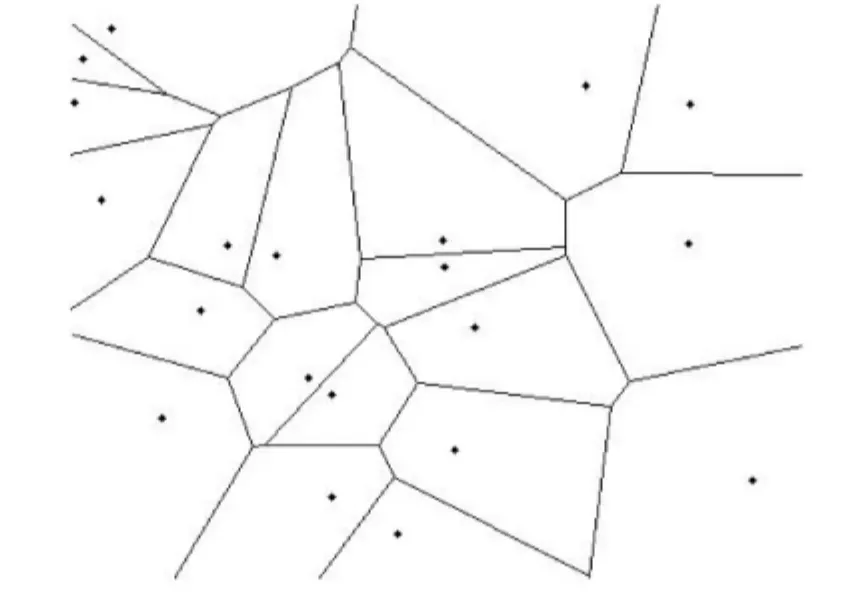
图2 Voronoi图

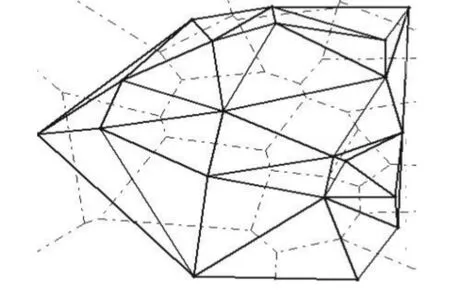
图3 Voronoi与Delaunay三角剖分关系

1.3 Delaunay三角剖分

最终形成最接近规格化的三角网格还要进行Delaunay三角剖分.根据文献［9］，Delaunay三角剖分的定义是：Voronoi图的一个顶点同时属于3个Voronoi多边形，每个Voronoi多边形内有且仅有一个节点.连接3个共点的Voronoi多边形分别对应的3个节点则形成一个Delaunay三角形，所有这样的三角形的集合就是Delaunay三角剖分.Delaunay三角剖分与Voronoi图互为对偶，图3是Delaunay三角剖分与Voronoi的关系图.

2 点云数据获取及三维重建

2.1 点云数据获取

本文采用XJTUOM三维光学面扫描系统获得人体的三维点云，XJTUOM的基本原理是：测量时光栅投影装置投影多幅多频光栅到待测物体上，成一定夹角的2个摄像头同步采得相应图像，然后对其进行解码和相位计算，并利用立体匹配技术、三角形测量原理［10］，解算出2个摄像机公共视区内像素点的三维坐标.

标定是借助于标定装置，利用软件算法计算出扫描头的所有内外部结构参数，才能正确计算测量点的坐标.标定算法采用平面模板八步法进行标定，所谓八步法就是在系统的标准测量距离下，依次采集8个不同方位的模板图象进行标定.其中400mm×300mm幅面的标准测量距离为1 000mm.

实验对于400mm×300mm的幅面，采用标定板进行标定，得到的标定极差为0.017 4，远小于系统要求的0.05，大大减小了测量误差.采用三维面扫描仪进行测量，从正面开始，对人体以15°进行旋转，并对每个角度进行从头到腰部的拍摄，进而得到了人体上身的点云，最终获得了49幅图像，最后用自带的点云处理软件进行数据处理，包括点云配准、融合、光顺、平滑处理的过程.

输出的文件以.PLY格式保存.但这种文件格式在Matlab中不能直接读取，因此，在Matlab平台上，利用斯坦福实验室提出的plyread函数，经过改进，将三维扫描仪获得的.PLY文件以逐行读取的办法转化成N*3矩阵的.MAT文件.由于得到的点云在百万级，还是很难进行三维重建操作，因此，本文提出一个适合人体数据精简的算法.

2.2 点云数据精简

现有的数据精简的基本算法主要有包围盒法、均匀网格法、三角网格法及曲率采样法等.传统的数据精简主要是采用包围盒法［11］，这种方法简单、高效，对于均匀的点云能够取得一定效果，但只适应于表面简单、曲率变化不大的物体的数据精简.减少三角网格数目的精简方法，适用于分块或完整三维数据，但首先需对数据点云进行三角网格化处理.基于“中值滤波”原理的均匀网格法，一些在形状急剧变化的表面处的点将会丢失.曲率采样法能较准确地保持模型的曲面特征并有效减少数据点，但一般计算效率较低.在最短的时间内，用最少的点表示最多的信息是是指精简的目标.精度、简度、速度是度量点云数据精简好坏的三个标准，精度是指精简后的点云拟合的曲面与原有人体曲面的相似度，简度是指精简后点云的个数比三维扫描仪获取点云的个数减少的程度，速度是指点云精简的全过程所花费的时间.这三者是很难同时满足的.

基于人体点云数据的特殊性质，考虑到人体的细节特征在毫米级上差别是不明显的，因此，对点云沿着高度层进行分层，以1mm的步长取数据，删除中间点，通过Matlab中的取整函数，将0.1mm的位进行四舍五入，从而将点云等分成N层，本次实验将人体等分成1 000层.在此后的三角化中，这样的简化并不会影响重建的细节信息，即点云精简的精度高.由于不需要计算曲率信息，计算比较简单，因而三维重建的速度很快.实验将1 032 494个点云精简到148 565个，点云数据达到十万级，就可以利于用Crust算法进行三维重建.

2.3 点云三维重建

定义1在点云S外面插入外壳F，外壳上的点到点云S上任一点的欧几里德距离都是点云上的点到外壳中轴最小距离的r倍，则称S为曲面F的r-sample.

定理1S为曲面F的r-sample，若r≤0.25，S的Crust图仅连接F上邻近的点.

定理2S为曲面F的r-sample，若r≤0.06，则S的Crust图包含一个三角剖分的网格收敛于F，Crust图上的每个点距离F上任一点p的距离小于5r·d(p)，其中d(p)是p到中轴的距离.

定义Vs是点云S的Voronoi顶点集.由于许多三维的Voronoi顶点不位于中轴附近，点云S在F上被其他点包围，Vs以点云S和它的邻近点的垂直平分平面为边界，分为两部分，每一部分都几乎垂直于F.因此，Vs的几何形状为长窄形状，且在样本点s处几乎垂直于F.Vs向外垂直延伸到中轴上，在中轴附近，其他F上样本点比点s更接近中轴，且Vs被切断.这就保证了Vs上其他一些顶点位于中轴附近.从而得到了以下的算法.

在Voronoi过滤阶段，不需计算所有的Voronoi顶点.对于每个样本点s，只需计算2个距离点s最远的Vs顶点，这2个顶点分别在外壳F的两侧，称为极点，用符号p+，p-表示.p+是Vs中距离点s最远的点，Vs的几何形状属于长窄形状，因此p-正好位于相反的方向.以下是Crust算法的基本步骤：

Step 1插入外壳F，实验取r=0.05.

Step 2计算点云S的Voronoi图.

Step 3对每个点s进行如下操作：(1)如果s不在凸壳上，则p+是Vs中距离s最远的Voronoi顶点.定义n+为矢量sp+.(2)如果s在凸壳上，定义n+为领域三角形外法矢量的平均值.(3)定义p-是在n+负向上，Vs中距离s最远的voronoi顶点.

Step 4P为所有极点p-与p+的合集.计算S∪P的Delanuary三角剖分.

Step 5仅保存3个顶点都在点云S上的三角形.

图4 重建前不同角度点云

图5 重建后不同角度的人体模型

3 结果与讨论

利用三维面扫描仪得到人体点云信息，在主频为3.10GHz，内存为4GB的PC机上，以Matlab为平台进行算法实现，结果如图4和图5所示，图4为重建前不同角度的点云，图5为重建后的人体模型.

本文标定算法采用平面模板八步法进行标定，在系统的标准测量距离下，依次采集8个不同方位的模板图象，标定极差为0.017 4.从实验结果看出，采集到了人体的各个角度的图像，验证了本实验测量系统的优势.

图4为点云精简后的点云，虽然看不到人体的细节，但是人体完整性还是得到了保障，人体轮廓明显，本次实验将1 032 494个点云精简到148 565个，验证了本文点云精简算法在精度、简度、速度方面的优势.

图5是图4的点云在基于Voronoi的Crust算法重构后的人体模型，从重构结果可以看出，文中算法给出的网格曲面可以清晰地还原人体外形的细节信息，如眼，嘴，鼻以及腹肌的曲线等.从重构时间看，1 032 494个点云用了不到26s，验证了本文算法在剖分速度方面的优势，表1为本文结果与来自斯坦福扫描实验室的实验数据的比较.从完整性看，本文算法完成了人体的360°无缝重建.

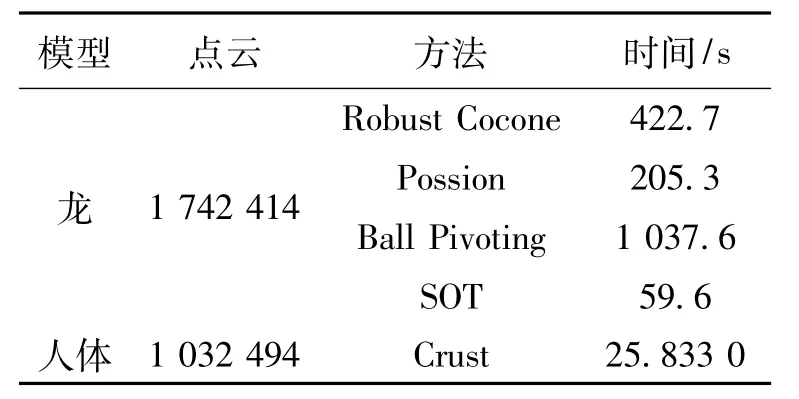
表1 算法比较结果统计

4 结束语

以上实验结果及分析表明，该三维重建系统能够解决曲面复杂，点云庞大的人体三维重建难题，并得到了360°无缝隙，曲线特征明显，轮廓分明的人体重建模型，且重建速度大幅度提高.在测量阶段，通过对三维扫描仪全方位标定，标定极差为0.017 4，为人体模型360°重建奠定了基础.在采集到49幅点云的基础上，经过点云配准，点云精简，使人体庞大的点云适用于Crust算法.利用Crust算法将1 032 494个离散的点云重建为人体模型，且仅用了不到26s.三维扫描仪的测量与人体三维重建的一体化系统有着广阔的应用前景，将为人们的生活提供更多的便利，不久的将来，人们足不出户就可以完成人体尺寸测量与三维试衣.

［1］胡智.基于三维重构的人体尺寸测量研究［D］.武汉：武汉纺织大学，2013.

［2］钱晓农，尹兵.基于三维人体测量的人体体型细分识别的研究［J］.纺织学报，2011，32(2)：107-111.

［3］LORENSEN W E，CLINE H E.Marching cubes：A high resolution 3D surface construction algorithm［J］//ACM Siggraph Computer Graphics，1987，21(4)：163-169.

［4］聂建辉，马孜，胡英，等.针对密集点云的快速曲面重建算法［J］.计算机辅助设计与图形学学报，2012，24(5)：574-582.

［5］倪小军.点云数据精简及三角网格面快速重构技术的研究与实现［D］.苏州：苏州大学，2010.

［6］HOPPE H，DEROSE T，DUCHAMP T，et al.Surface reconstruction from unorganized points［C］//ACM SIGGRAPH 1992 Proceedings，1992：71-78.

［7］AMENTA N，BERN M，KAMVYSSELIS M.A new voronoi-based surface reconstruction algorithm［C］//Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques.ACM，1998：415-421.

［8］马秀丽，李金博，周峰，等.心内膜表面几何模型三维重建算法研究［J］.计算机应用研究，2013，30(8)：2530-2533.

［9］熊捏阳，陈晓波，孙健，等.结构光投影面部三维测量系统的研制［J］.上海交通大学学报：医学版，2009，29(7)：837-841.

［10］杨斌.基于人体的点云数据处理与虚拟人体建模研究［D］.北京：北京服装学院，2012.

［11］宋洋，孙殿柱，刘晓红，等.物体表面采样数据近似最小包围盒快速求解［J］.农业装备与车辆工程，2012，50(4)：1-5.

The access of point clouds and the reconstruction of the 3D body

LI Peng-fei1，HOU Yi-xing1，JING Jun-feng1，2

(1.School of Electronic＆Information，Xi'an Polytechnic University，Xi'an 710048，China; 2.Shaanxi Research Center of Automation of Textile Printing＆Dyeing，Xi'an 710048，China)

For the problem of complex body surface and the huge point cloud in reconstruction of three-dimensional human body，based on three-dimensional Voronoi diagram and the use of Delaunay triangulation，the Crust algorithm is proposed in this paper.49 point clouds'pictures of different angles and heights are achieved with the use of three-dimensional surface xjtuom scanner，and the registration are obtained with the software which is supported by the scanner.Then via Matlab platform，reading point cloud，point cloud compression and the 3D reconstruction are completed based on the crust algorithm，which confirm the correctness of the topology and convergence.Experiments prove that the system of three-dimensional reconstruction can achieve the complete triangulation of massive point cloud and the reconstruction of complex freeform human body，and the human model is achieved in any angle.

triangulation;simplification of point clouds;Crust algorithm;three-dimensional reconstruction

TP 391.41

A

1674-649X(2014)01-0072-05

编辑：武晖;校对：师琅

2013-10-23

陕西省教育厅科研计划项目资助(2013JK1084);陕西省科技厅科技攻关项目资助(2013K07-32)

李鹏飞(1962-)，男，陕西省西安市人，西安工程大学教授，主要从事机器视觉与图像处理等方面的研究.E-mail：992533034@qq.com.