基于小波变换的交流系统串联电弧故障诊断
2014-06-22刘晓明曹云东侯春光王丽君
刘晓明 赵 洋 曹云东 侯春光 王丽君
(沈阳工业大学电气工程学院 沈阳 110870)
1 引言
随着现代工业的发展,居民用电量的不断增加,电气火灾已成为造成人身安全及财产损失的巨大隐患。据《2010年中国火灾统计年鉴》统计,全国每年因电气原因引起的火灾占火灾总数的 30.7%。根据美国NEC标准,在用电系统低压用户端,并联电弧和接地电弧的回路电流一般大于75A,现有的保护断路器已具备隔离保护能力;而作为引发电气火灾主要原因的串联电弧故障,因受到线路负载的限制,其回路电流的有效值往往与负载正常工作回路电流有效值相近,均在5~30A之间[1],传统保护方法无法有效实现对串联电弧故障的隔离保护,进而可能引起电气火灾事故。因此,串联电弧故障的检测与诊断对电气设备的安全运行尤为重要。
目前,针对串联电弧故障的检测方法主要分为两类:一类是利用电弧放电时所引发的光、热、声音和电磁辐射等间接参数对其进行特性检测[2,3],文献[3]通过模拟实验研究,将早期弧声信号进行小波分解建立“弧声能量-信号”的映射关系,实现对电弧故障的早期预警。但由于测量传感器只能对特定位置进行检测而实际线路或设备中故障电弧发生点不确定,在实际检测应用中存在困难;另一类是对故障电流信号进行分析,判定线路中是否发生串联电弧故障[4-6],此类方法解决了对传感器安装位置的限制。文献[4]中采用自回归(Auto Regressive,AR)参数模型提取出 AR模型参数,结合欧式距离平方d2的方法,识别低压串联电弧故障,并给出回路识别的参考矢量。文献[5]根据故障电弧模拟实验,利用小波变换理论对电流信号的能量进行分析,以能量变比作为判据检测故障电弧。
随着人工神经网络的迅速发展,BP网络因其可实现输入输出的非线性映射已成为绝大部分神经网络模型的基础而被广泛应用[7,8]。由于传统BP网络存在收敛速度慢、局部极小点等不足,因此,本文基于阻尼最小二乘法对BP网络进行改进[8],并以不同负载下电弧故障模拟实验采得的电流信号作为故障分析和研究的物理参数,结合小波变换模极大值实现对低压串联电弧故障的综合诊断分类。
2 实验平台的搭建及数据采集
2.1 故障电弧发生器的设计
故障电弧发生装置是电弧故障模拟实验的重要组成部分。图1为本文参照UL1699—2008 AFCI标准[9]设计搭建的故障电弧发生器。该装置采用直径为8.0mm的石墨电极作为静触头,直径为10.0mm的铜电极作为动触头。动侧导电杆由PIC18F452型微控制器驱动57BYGH混合式步进电机实现运动,触头间最小步距达到0.1mm。

图1 可调控电弧发生器Fig.1 The controlled arc generator
2.2 串联电弧故障模拟实验
串联电弧故障的故障电流信号随负载的不同而不同。为研究电弧故障特征,本文以阻性负载(26.5Ω、46.8Ω)、阻感性负载(26.5Ω+34.4mH、46.8Ω+34.4mH)以及非线性负载(200W空载旋转电机、300W台式计算机和2 000W电磁炉)作为实验负荷进行串联电弧故障模拟实验。实验电路原理如图2所示。

图2 实验电路原理图Fig.2 Principle diagram of experimental circuit
图3为一组线性和非线性负载的实测波形。对比可知,两种负载的故障电流波形在过零前后均发生畸变,且存在明显的“零休”现象。为寻找不同负载下电弧故障的共性特征并获取更多的网络训练样本,本文对同一负载进行10次试验并采集正常和故障情况下的电流数据各10组。
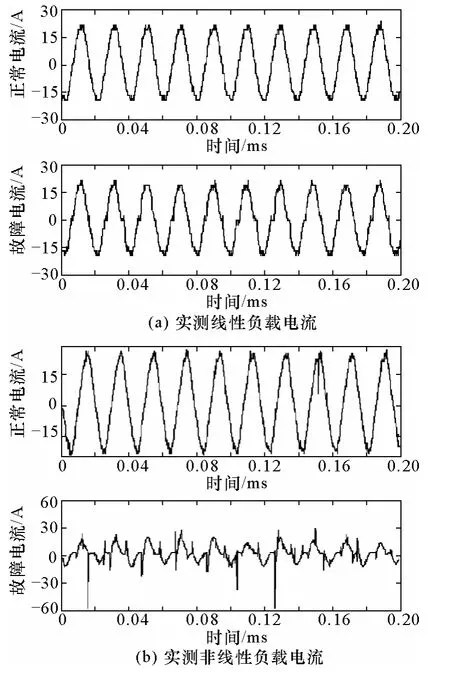
图3 实测线性和非线性负载电流Fig.3 Linear and nonlinear load current waveform in test
3 串联电弧故障的特征提取
在信号分析处理中,小波变换理论以其良好的局部化性质[10-12]弥补了傅里叶变换分析局部时域信号的不足。通过对不同频率成分采用逐渐精细的采样步长实现对高、低频信号及信号任意细节的有效检测,基于小波变换理论,本文将信号中提取出的各频段细节信号模极大值作为神经网络的输入特征向量进行网络训练。
3.1 小波模极大值理论
串联电弧故障发生前后故障电流存在“零休”现象,相比于正常电流,故障电流信号存在明显的奇异性。根据信号奇异性检测理论[13,14],作为表征信号奇异性的Lipschitz指数,其正则性与小波变换幅值随尺度的衰减性相关。因此,对于信号在任一点x处的局部Lipschitz正则性,即依赖于x邻域内小波系数模|WTf(a,b)|在细节尺度下的衰减性,而实际工程中多是利用局部极大值对其进行度量。因此,对信号奇异性的检测即可通过寻找在细节尺度下的小波模极大值进行判定。
设φ(t)∈L2(R)(L2(R)为平方可积的实数空间),其傅里叶变换为ψ(x),函数ψ(x)若满足以下允许条件

则称φ(x)为一个基本小波。则平方可积函数f(t)的连续小波变换为

式中,a为伸缩因子,a≠0;b为平移因子;φ*(t)为φ(t)的共轭函数。
将伸缩因子a和平移因子b进行离散化处理,得到离散小波变换

式中,j为尺度系数,j=0,1,…,k;k∈Z。
与傅里叶时频窗口不同,小波变换的时频窗口中心为(b,±ω0/a),时窗宽度和频窗宽度分别为aΔφ和Δψ/a,窗口形状为两个矩形[b -aΔφ ,b +aΔφ ]×[(±ω0-Δψ ) / a ,(± ω0+Δψ )/a]。
若基础小波φ(t)具有 n阶消失矩且是紧支集,则一定存在紧支集函数(平滑函数)φ(t),使得,则式(2)、式(3)可写成
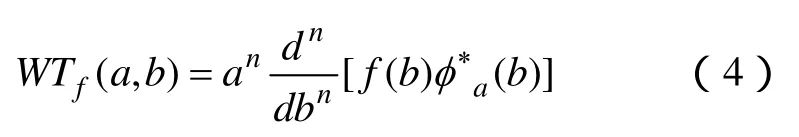
分析式(2)~式(4)可知,小波系数可认为是信号经平滑函数处理后的n阶导数值,则其小波模极大值就对应于处理后n阶导数的极大值。因此,当小波系数的模为极大值时,其对应点即为信号的奇异点。
3.2 信号的阈值降噪
由于电弧燃烧具有极大的不稳定性和随机性以及信号采集过程中混入的高频干扰信号,会干扰信号奇异特征的提取,影响电弧故障特征提取的准确性。为消除信号分析过程中因上述问题引起的样本奇异,经比较本文采用极大极小原理结合小波阈值降噪功能对信号进行阈值降噪处理,将未降噪信号作为未知回归函数估计式,通过产生一个最小均方误差的极值实现最大均方误差最小化,使估计结果更加准确,提高降噪效果。阈值选取规则如下:

图4为将图3进行降噪处理后的电流波形。对比发现:利用该方法在降噪滤波的同时保留了故障电流在“零休”处的特征。
基于小波模极大值理论,本文采用三阶Daubechies(db3)小波基对降噪后的信号进行五层分解得到逼近信号a5与细节信号d1~d5共六组频段信号。由于a5频段信号表征了原始信号经小波变换后的逼近情况,其模极大值相比其他频段有较大差异,会导致数据处理过程中的样本奇异。为便于数据分析并满足神经网络训练要求,本文对 d1~d5频段细节信号的模极大值进行数据处理。表1~表3为处理后阻性、阻感性和非线性负载各频段模极大值的特征向量。

图4 降噪后线性和非线性负载电流波形Fig.4 Denoised current waveform of linear and nonlinear loads

表1 阻性负载特征向量Tab.1 The characteristic vectors of resistive loads
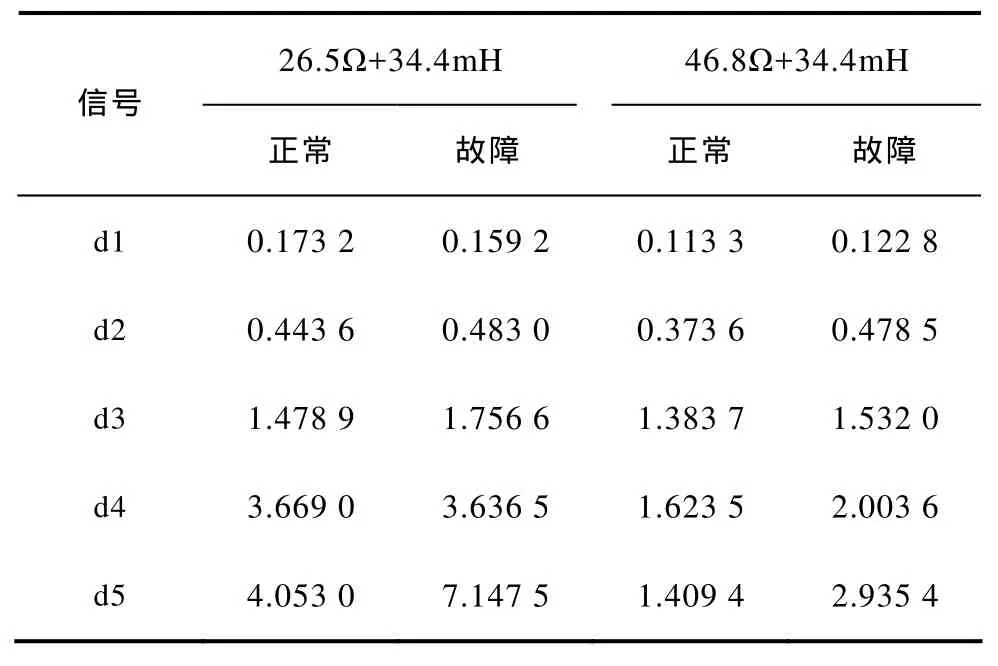
表2 阻感性负载特征向量Tab.2 The characteristic vectors of resistive and inductive loads
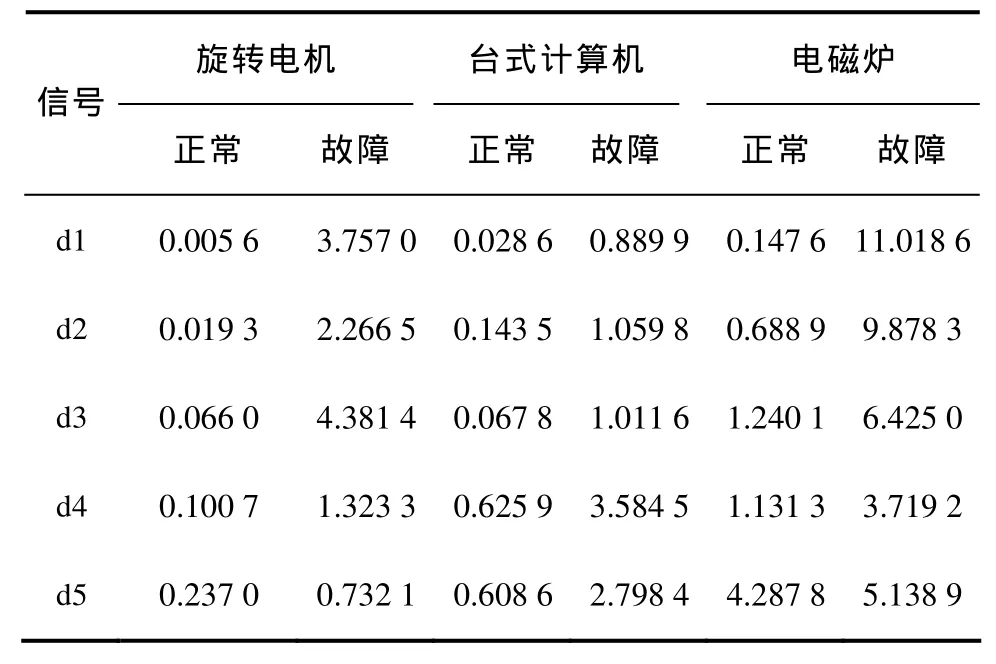
表3 非线性负载特征向量Tab.3 The characteristic vectors of nonlinear loads
4 改进BP神经网络的串联电弧故障诊断
4.1 基于阻尼最小二乘法的改进BP网络训练方法
作为一种多层前馈型神经网络,传统的 BP神经网络因对网络结构和初始值过于敏感,使其存在收敛速度慢、局部极小点等缺陷。为解决上述不足,本文基于阻尼最小二乘法,采用近似替换 Hessian阵的训练方法改进BP网络。Hessian阵近似替换为

其梯度为

式中,J为雅克比矩阵,是权值和阈值的函数;e为网络训练误差向量。
则迭代方程为

当 μ=0时,上式就变成具有近似 Hessian阵的牛顿法。当μ较大时,则接近小步长的梯度法。
网络训练中,基于阻尼最小二乘法采用正切 S型传递函数和纯线性传递函数作为隐层和输出层的传递函数,设置最大训练次数为10 000,训练精度为1e-5,最小梯度为1e-8。
4.2 基于改进BP神经网络的串联电弧故障诊断
基于小波变换理论,对信号各频段进行小波模极大值处理,以此作为网络的前处理方法为神经网络提供输入特征向量,并选用三层 BP神经网络,实现对串联电弧故障的诊断分类。设置输入层神经元个数为 5,输出层神经元个数由实际需要决定。则隐层神经元个数与输入层神经元个数和输出神经元个数之间的近似关系为

式中,n1为隐层神经元个数;n2为输入层神经元个数;n3为输出神经元个数;a为[1,10]之间的数。
4.2.1 线性负载的诊断分析
本文采用4种线性负载,取表1、表2中的特征向量作为测试样本,取实验中其他九组线性负载的正常和故障特征向量作为网络的输入样本。输出层采用2个神经元,输出状态为:阻性正常(1,0);阻性故障(1,1);阻感性正常(0,0);阻感性故障(0,1)。
图5为线性负载下网络训练的收敛情况。经115次训练,网络达到训练精度要求。网络测试的输出结果见表4。可以看出,网络输出结果与期望值接近,最大误差为 0.79%,实现并验证了对线性负载串联电弧故障的有效诊断分类。

图5 线性负载神经网络训练过程Fig.5 Neural network training process of linear loads

表4 线性负载神经网络测试结果Tab.4 Neural network test result of linear loads
4.2.2 非线性负载的诊断分析
本文采用3种非线性负载,取表3中的特征向量作为测试数据,取其他九组非线性负载的正常和故障特征向量作为网络的输入样本。输出层采用 4个神经元,输出状态为:旋转电机正常(0,1,0,1);旋转电机故障(1,1,0,1);台式计算机正常(1,1,1,0);台式计算机故障(1,1,1,1);电磁炉正常(1,0,1,0);电磁炉故障(1,0,1,1)。
图6为非线性负载下网络训练的收敛情况。经22次训练,网络达到训练精度要求。网络测试的输出结果见表 5。可以看出,网络输出结果与期望值接近,最大误差为 0.80%,实现并验证了对非线性负载串联电弧故障的有效诊断分类。

图6 非线性负载神经网络训练过程Fig.6 Neural network training process of nonlinear loads

表5 非线性负载神经网络测试结果Tab.5 Neural network test result of nonlinear loads
4.2.3 线性与非线性负载的综合诊断分析
为丰富网络的诊断范围,实现对线性与非线性负载的综合诊断分类,在保证训练精度的同时整合两类输入特征向量,并调整输出层神经元为2个,设置训练精度为1e-5,最小梯度设置为1e-8,输出状态为:线性故障(0,1);非线性故障(1,0);正常(0,0)。
图7为综合负载下网络训练的收敛情况,由于训练精度要求高及输入数据类型复杂,导致训练次数有所增加,但网络收敛情况良好,经634次训练,网络达到训练精度要求。选用表1~表3中的特征向量对网络进行测试,输出结果见表 6。可以看出,网络输出结果与期望值接近,在规定的训练精度及最小梯度内,最大误差仅为 0.18%,实现并验证了对串联电弧故障的综合诊断分类。

图7 综合负载神经网络训练过程Fig.7 Neural network training process of composite loads
4.2.4 对未知负载串联故障的诊断识别
上述测试结果虽验证了网络的有效性,但由于测试样本与训练样本均由网络已知的负载实验提取,并未证明其对未知负载故障诊断的实用性,而实际末端用电负荷往往是未知的。为验证网络的实用性,本文分别以 12.8Ω、12.8Ω+6mH、20W空载旋转电机、800W微波炉以及2 000W吸尘器的正常与故障各10组数据作为未知负载对网络进行验证。图8为标于坐标平面上的网络测试结果。
图中 p(1),p(2)表示网络输出的两列测试结果,可以看出网络对未知负载的诊断分类依然明显,测试结果均集中在相应的期望值区域附近,但由于负载未知,最大偏差值为13.21%。

图8 网络测试结果Fig.8 The network test results
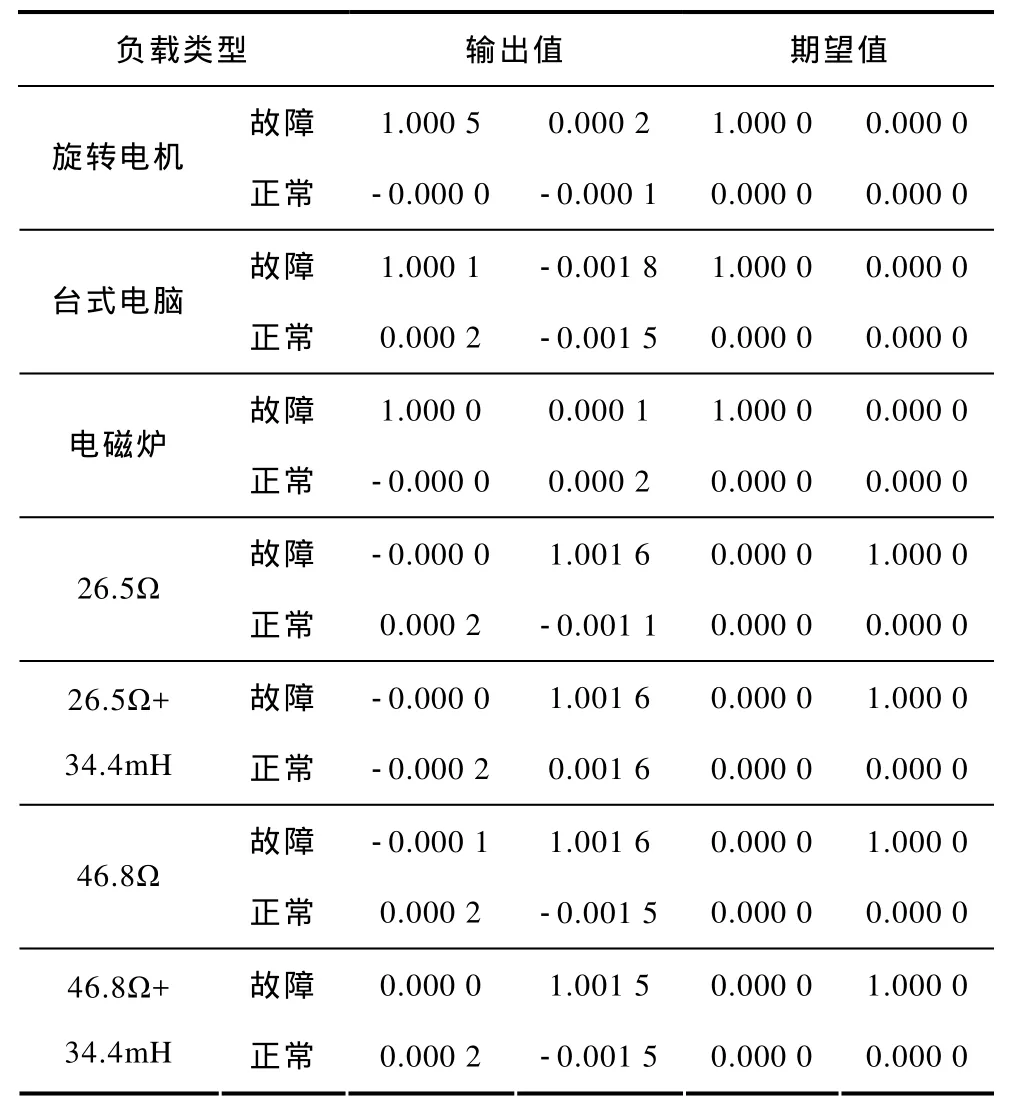
表6 综合负载神经网络测试结果Tab.6 Neural network test result of composite loads
5 结论
通过对串联电弧故障进行模拟实验,并结合小波变换原理与改进的 BP神经网络构建起输入特征向量与电弧故障的映射关系,解决了串联电弧故障的综合诊断分类问题。将电流信号经小波变换后得到不同频段下的模极大值作为神经网络的输入特征向量对网络进行训练。结果表明,网络对串联电弧故障具有较好的诊断与分类能力。
[1] Carlos E Restrepo.Arc fault detection and discrimination methods[C].The 53rd IEEE Holm Conference,2007: 115-122.
[2] Malakondaiah Naidu,Thomas J Schoepf,Suresh Gopalakrishnan.Arc fault detection scheme for 42V automotive DC networks using current shunt[J].IEEE Transactions on Power Electronics,2006,21(3):633-639.
[3] 蓝会立,张认成.基于小波分析的故障电弧伴生弧声特征提取[J].电力系统及其自动化学报,2008,20(4): 57-62.Lan Huili,Zhang Rencheng.Study on the feature extraction of fault arc sound signal based on wavelet analysis[J].Proceedings of the CSU-EPSA,2008,20(4): 57-62.
[4] 雍静,桂小智,牛亮亮,等.基于自回归参数模型的低压系统串联电弧故障识别[J].电工技术学报,2011,26(8): 213-219.Yong Jing,Gui Xiaozhi,Niu Liangliang,et al.Series arc fault identification in low voltage system based on autoregressive parameter model[J].Transactions of China Electrotechnical Society,2011,26(8): 213-219.
[5] 孙鹏,董荣刚,郑志成.基于小波分析信号特征频段能量变比的故障电弧诊断技术研究[J].高压电器,2010,46(7): 46-50.Sun Peng,Dong Ronggang,Zheng Zhicheng.Arc fault diagnosis technology based on the analysis of energy variation of signal’s characteristic frequency band with wavelet transform[J].High Voltage Apparatus,2010,46(7): 46-50.
[6] 孙鹏,郑志成,闫容妮,等.采用小波熵的串联型故障电弧检测方法[J].中国电机工程学报,2010,30(S1): 232-236.Sun Peng,Zheng Zhicheng,Yan Rongni,et al.Detection method of arc fault in series with wavelet entropy[J].Proceedings of the CSEE,2010,30(S1):232-236.
[7] 何怡刚,祝文姬,周炎涛,等.基于粒子群算法的模拟电路故障诊断方法[J].电工技术学报,2010,25(6): 163-171.He Yigang,Zhu Wenji,Zhou Yantao,et al.An analog circuit diagnosis method based on particle swarm optimization algorithm[J].Transactions of China Electrotechnical Society,2010,25(6): 163-171.
[8] 周天春,杨丽君,廖瑞金,等.基于局部放电因子向量和 BP神经网络的油纸绝缘老化状况诊断[J].电工技术学报,2010,25(10): 18-23.Zhou Tianchun,Yang Lijun,Liao Ruijin,et al.Diagnosis of aging condition in oil-paper insulation based on factor vectors of partial discharge and BP neural network[J].Transactions of China Electrotechnical Society,2010,25(10): 18-23.
[9] UL standard for safety for arc fault circuit interrupters[S].2ed.ANSI UL1699,2008.
[10] George D Gregory,Kon Wong,Robert F Dvorak.More about arc-fault circuit interrupters[J].IEEE Transactions on Industry Applications,2004,40(4):1008-1009.
[11] Yummei G,Li W,Qi Zhuo,et al.Wavelet packet analysis applied in detection of low-voltage DC arc fault[C].Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications,2009: 4013-4016.
[12] 于志伟,苏宝库,曾鸣.小波包分析技术在大型电机转子故障诊断系统中的应用[J].中国电机工程学报,2005,25(22): 158-162.Yu Zhiwei,Su Baoku,Zeng Ming.Application of wavelet packet in fault diagnosis system of large scale DC motor rotor[J].Proceedings of the CSEE,2005,25(22): 158-162.
[13] James A Momoh,Robbert Button.Design and analysis of aerospace DC arcing faults using fast Fourier transformation and artificial neural network[C].Power Engineering Society General Meeting,2003: 791-792.
[14] Mallat.A wavelet tour of signal processing[M].北京:机械工业出版社,2002.
[15] Li Dongwei,Song Zhengxiang,Wang Jianhua.A method for residential series arc fault detection and identification[C].Proceedings of the 55th IEEE Holm Conference on Electrical Contacts,2009: 8-14.
[16] 李夏青,左丽.直流牵引网故障电流能量谱及特征矢量[J].电工技术学报,2010,25(11): 164-168.Li Xiaqing,Zuo Li.Energy spectrum and eigenvector of DC traction power supply short-circuit current[J].Transactions of China Electrotechnical Society,2010,25(11): 164-168.
[17] Kolker D,Campolo S,DiSalvo N.A study of time/current characteristics of the ignition processes in cellulosic material caused by electrical arcing for application in 240V arc-fault circuit interrupters[C].Proceedings of the Fifty-Third IEEE Holm Conference on Electrical Contacts,2007: 105-114.
