基于遗传优化支持向量机的变压器绕组热点温度预测模型
2014-06-22陈伟根2刘彭尚怡孙才新
陈伟根 滕 黎,2刘 军 彭尚怡 孙才新
(1.重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400030 2.国家电网重庆市电力公司市区供电分公司 重庆 400015)
1 引言
电力变压器是电网中能量转换的核心,是电网中最重要和最关键的设备之一。电力变压器的使用年限和可用寿命很大程度上取决于其及时地将变压器内部产生的热量散发至周围环境中的能力,也即是变压器的热特性。变压器负载值最主要的限制因素是绕组热点温度,其温度值不能超过允许值,否则会对变压器的绝缘寿命造成很大损害。因此,准确地获取变压器绕组热点温度是保证变压器安全、高效、可靠运行的关键。
目前,国内外对变压器顶层油温和绕组热点温度计算与预测研究较多[1-4]。最常用的方法是 IEEE C57.91导则和IEC 354导则推荐的计算公式[5,6],但推荐公式忽略了环境温度变化对顶层油温和热点温度计算的动态影响从而计算精度需要提高。为此,文献[7]考虑环境温度变化对顶层油温的影响改进了 IEEE推荐公式。文献[8,9]运用热电类比方法将变压器内热传导过程类比电路模型建立了反映变压器物理过程的顶层油温和热点温度计算模型,使用模型时需要变压器的传热参数。文献[10]运用数值计算方法建立了变压器的理论热模型,利用有限积分变换技术解决热传导边界值问题,模型不仅需要变压器实际电气参量,还需要实际的设计数据。近年来,应用人工智能方法对变压器顶层油温或绕组热点温度进行预测较为常见的是人工神经网络,而应用支持向量机方法对其预测的文献并不多见。文献[11,12]运用神经网络对变压器顶层油温、绕组热点温度进行预测,但输入和输出之间的非线性拟合缺乏实际的物理意义,训练过程易陷入局部极小值点。文献[13]初步将最小二乘支持向量机用于对变压器顶层油温的预测,但模型参数采用默认值而不是最佳参数组合。
支持向量机(Support Vector Machine,SVM)是一种基于小样本统计学习理论和结构风险最小化的建模方法[14],是继神经网络研究后机器学习领域的研究热点,在电力负荷预测、变压器故障诊断等领域取得较好的应用成果[15,16]。由于 SVM 不仅克服了其他机器学习方法的过学习、欠学习、维数灾、泛化能力不高和局部极小值等缺点,且泛化能力更好。在实际应用中 SVM 相关参数一般依靠经验人为选取,而参数的选取直接关系到 SVM 的预测精度。遗传算法(Genetic Algorithm,GA)具有很强的鲁棒性和全局优化搜索能力,适合复杂的优化问题,为此,文中利用遗传算法对SVM参数寻优。
根据变压器内部温度采集数据具有小样本的特点,且绕组热点温度具有随时间变化呈现高度非线性的特点,因此,采用GA-SVM来建立变压器绕组热点温度非线性预测模型是合理的。本文将实测变压器负载电流、环境温度以及4个易测点和关键点特征温度,即顶层油温、底层油温、油箱上死角温度、油箱下死角温度,共6个特征量作为输入变量,绕组热点温度作为输出变量,并随机划分模型的训练集和预测集,对比GA-SVM模型、前馈型BP神经网络以及反馈型Elman神经网络的热点温度预测结果,实验结果表明,GA-SVM模型预测值与实测值更吻合,预测性能和精度更高。
2 模拟温升变压器绕组温度测量实验室平台
试验是在已搭建的基于热电偶和光纤光栅传感器的单相油浸式变压器测温平台上完成的,试验接线如图1所示。图1中调压器型号为KZT-10kVA/0.25kV,试验变压器型号为 YD-100kVA/5kV,光纤光栅传感器选用宁波杉工的高电压环境 FBG温度传感器FBG-HV-T01,热电偶选用镍铬-镍硅热电偶。

图1 试验接线图Fig.1 Test circuit connection diagram
试验分别由重庆大学高电压与绝缘技术系自行研究设计的“变压器绕组温度分布特性多通道温度采集系统”和光纤光栅温度传感器温度采集系统采集数据。在光纤光栅温度传感器采集系统中耦合器两个输出端分别连接温度测量光纤和参考光纤,光信号经滤波器解调和光电信号放大电路转换,再由数据采集卡采集光电探测器中的电压值,最后输入计算机进行处理。热电偶多通道温度采集系统采集数据通过 RS-232串行通信方式直接输入到计算机中。
由于变压器内的热点温度位置的不确定性,经过反复试验、不断调整比较得出热电偶和光纤光栅温度传感器的布置方式和位置。具体是在油浸式变压器内部紧靠绕组线饼各层以及油箱壁共放置 21个热电偶,另外分别放置5个热电偶测量具有代表性的变压器顶层油温、底层油温、油箱顶部上死角、油箱底部下死角以及周围环境温度。为对比热电偶的测量结果,将光纤光栅传感器放置在多次试验中热点温度常出现的绕组线饼层,同时绕组顶部和底部线饼层也有布置。变压器配有循环油泵以及油路系统,可以通过打开油泵来驱动变压器内部油流循环达到模拟不同油流下的流速。试验采用短路接线等效试验法,低压端短路,高压端接输入电流,通过改变短路电流大小来模拟变压器在不同负载下的发热情况。
先将调压器输出电流大小调为油浸式试验变压器的输入电流的额度值,关闭油泵,变压器为自然油循环自然空气冷却方式;再在额度负载电流下持续进行试验26小时,考虑试验数据的一致性,在额度负载电流条件下分别做两次试验对比,每次均持续进行26小时,每隔4分钟采集一次数据,共采集390组温度数据。
3 绕组热点温度SVM模型的建立
为了不失一般性,对第2节中额定负载电流下试验得到的390组数据样本随机分为365组训练集样本,25组预测集样本。将变压器负载电流 I、环境温度 θa、顶层油温 θtop、底层油温 θb、上死角温度θ1、下死角温度θ2共6个特征量作为支持向量机模型的输入量 xi=[I,θa,θtop,θb,θ1,θ2]i,绕组热点温度θhs作为模型的输出量 yi=[θhs]i,因此 365组训练样本集为{(xi,yi),i=1,2,…,n,n=365}。支持向量机通过非线性映射φ(x)函数将输入空间的样本x映射到高维特征空间H中,并在高维特征空间H中利用结构风险最小化原则建立线性回归函数式中,w为权值向量,w∈H;b为偏置,b∈R;y'为预测值;y为实测值。

用SVM解决回归拟合问题时,在SVM分类的基础上引入 ε线性不敏感损失函数而得到回归型SVM。考虑允许拟合误差,引入松弛因子 ξi,ξi*。利用结构风险最小化原则,求解回归问题就转化为最小化结构风险目标函数的问题,即求使目标函数极小化的w和b的值

式中,常数C>0为惩罚因子。
求解式(2)时,通过引入非负的 Lagrange乘子构造 Lagrange函数,则问题转化为求 Lagrange式的鞍点,分别对式中各变量求偏导数并令其为零,利用对偶原理,转化为求解对偶问题。

进而可求得支持向量机非线性回归函数
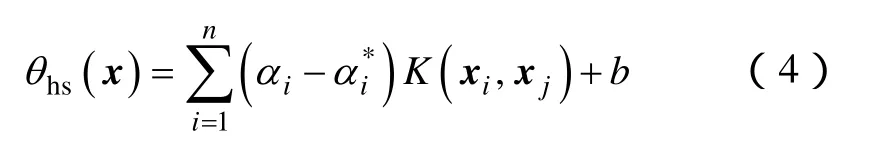
式中,αi、为引入非负的 Lagrange乘子;K( xi,xj)为满足 Mercer条件的核函数,其定义为 K( xi,xj)=φ( xi)·φ( xj),核函数的引入取代了高维空间中的点积,避免了对非线性映射函数φ(x)的求解,从而大大减少了计算量和复杂度。
不同的核函数对应不同的SVM,常用的核函数大致有四类:sigmoid核函数、径向基核函数、多项式核函数和线性核函数。其中,径向基函数(Radial Basis Function,RBF)的参数在有效范围内改变时不会使空间复杂度过大且易实现 SVM 的优化过程,它的每一个基函数的中心对应着一个支持向量,它们及输出权值均由算法自动确定[17]。考虑到 RBF核函数的优点[18]以及后面GA优化SVM,本文采用RBF核函数

式中,γ>0为核参数;|| xi-xj||为欧式范数。

图2 SVM回归结构图Fig.2 Structure of SVM regression
回归型支持向量机结构与神经网络的结构较为类似,其结构示意图如图2所示。图2中,输出的绕组热点温度θhs是中间节点的线性组合,每个中间节点对应一个支持向量,x1,x2,…,xn为输入变量,αi-αi*为网络权重。
4 基于GA-SVM的绕组热点温度预测
4.1 GA优化热点温度SVM模型参数
在本文研究中发现,建立非线性回归 SVM 预测模型需要确定的学习参数为惩罚因子C和核参数γ,其选取原则和取值直接对模型预测精确程度有很大的影响。当C大于一定值则对训练误差大于ε的样本惩罚越大,模型的泛化能力变差;当C小于一定值则对样本惩罚就越小,而使训练误差变大,模型的泛化能力变好。采用RBF核函数时,由径向基神经网络导出核参数 γ的影响,γ越大则支持矢量间影响较强,易造成欠学习;γ越小则易产生过学习,同时模型过于复杂,泛化能力变差。
为了使 SVM 有最优的性能,本文采用遗传算法对SVM模型的惩罚因子C和核参数γ进行寻优,避免人为选择参数的盲目性。遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、自适应的全局优化概率搜索算法,已被广泛应用于组合优化、机器学习、信号处理等领域[19,20],其主要步骤是编码、初始群体的生成、适应性值评估、选择、交叉、变异。遗传算法的4个运行参数取值范围:种群规模一般取 20~100;进化次数一般取100~500;交叉概率一般取 0.4~0.9;变异概率一般取0.01~0.03。
本文将参数C和γ使用二进制编码,寻优区间分别设定为[0,50]和[0,500],选择算子采用随机遍历抽样,交叉算子采用单点交叉算子,变异算子采用基本位变异算子,种群规模20,最大进化次数200,交叉概率为0.6,变异概率为0.03,判断终止精度为 10-4。
文中采用均方误差(Mean Squared Error,MSE)、平均相对误差eMAPE和相关系数R三个指标来评价模型的性能和预测效果,R为区间[0,1]上的值,当MSE和eMAPE值越小且R越接近1,表明模型预测性能越好。即有

式中,训练集进行训练仿真的MSE作为优化算法适应度函数时,s为训练集样本个数n;预测集进行预测仿真的MSE作为评价模型预测性能指标时,s为预测集样本个数m。
4.2 GA-SVM模型的预测步骤
采用支持向量机回归方法与遗传算法相结合的电力变压器绕组热点温度预测步骤如下:
(1)数据样本归一化。由于数据样本中各变量差异较大,具有不同的量纲,在建立 SVM 回归模型前对训练集和预测集样本归一化到[0,1]区间,计算公式为x'=(x-min(x))/(max(x)-min(x)),式中x、x'分别为归一化前、后的值。
(2)GA寻优SVM参数。将训练集样本作为控制量仿真,进行二进制编码并创建初始种群,将在交叉验证意义下训练集的MSE作为GA的适应度函数并对适应度定标;进行选择、交叉、变异操作,判断是否满足终止精度或当前迭代次数是否等于最大迭代次数,若满足则解码输出最优参数C和γ,否则重新进行遗传操作。
(3)建立SVM回归模型及预测。根据第(2)步得到最佳参数[C,γ],采用RBF核函数训练SVM回归建模,把训练集训练得到的模型对预测集样本回归预测并对数据反归一化处理。
(4)评价预测模型性能指标MSE、eMAPE和R,若不符合要求则转至第(2)步,重新设定遗传算法参数。
(5)比较真实值与预测值,得到对应模型的指标 MSE、eMAPE和R。
5 结果对比及分析
5.1 参数优化对比
寻优最佳参数[C,γ]为优化算法的适应度较小值对应的组合,为比较参数优化效果,对训练集运用多次交叉验证(K-fold Cross Validation,K-CV)的思想,分别采用网格搜索寻优法和GA对参数寻优对比见表 1。利用网格搜索寻优法时,先粗略寻找最佳参数,再进行精细的参数选择,交叉验证的初始化分组数K为 5,参数 C和 γ初始搜索范围分别为[2-10,210]和[2-10,210],搜索范围对应的步进大小值均设为20.5,判断终止精度为10-4。

表1 网格搜索和GA优化模型参数对比Tab.1 Comparing parameters optimized by grid-search and GA
从表1可以看出,两种优化算法利用训练样本对模型参数C和γ寻优后GA的适应度值8.55×10-4最小,模型的适应能力最好,对应的参数[C,γ]=[1.16,0.28]组合最佳。
由GA寻找最佳参数的适应度变化曲线图3可知,进化代数为200次时终止进化,此时适应度值8.55×10-4就接近理想最优值。

图3 GA优化SVM模型参数Fig.3 Optimizaction of SVM model parameter using GA
为比较本文提出的 GA-SVM 热点温度模型的性能,分别采用前馈型BP神经网络和反馈型Elman神经网络[21]建模对相同的样本集进行训练和预测。GA-SVM模型选用RBF核函数,经反复参数寻优,得到满足要求的C和γ分别为1.16和0.28。利用神经网络预测时,经过反复试验,BP网络和 Elman网络设置相同,网络的输入层、隐含层、输出层的节点数分别为6、13、1,隐含层传递函数选用tansig函数,输出层传递函数选用logsig函数,训练函数选用Levenberg-Marquardt算法,学习速率Lr=0.01,目标误差Eg=0.001。三种模型下绕组热点温度预测值与实测值比较见表 2,可以得出,本文模型有较强的泛化能力,根据训练集输入输出样本学习后,对不在训练集中的预测输入样本进行预测,得出相应预测输出值与实测值吻合很好。
5.2 预测结果分析
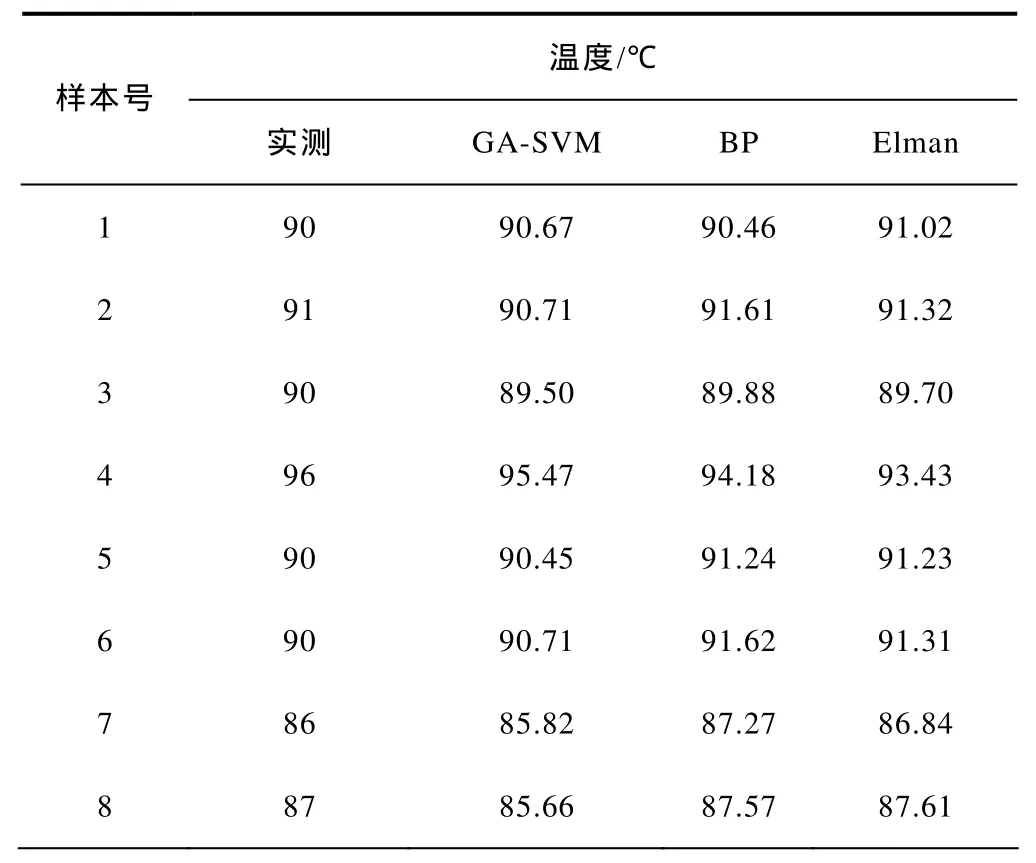
表2 不同模型下预测值与实测值比较Tab.2 Contrast the measured data and predict data of different models

(续)
图4列举了GA-SVM、BP和Elman网络预测值与实测值的相对误差曲线,由图4可知,三种模型的预测值与实测值的最大相对误差分别为1.5%、2.2%和2.7%。最小相对误差分别为0.008 2%、0.02 9%和0.18%,均在允许误差范围内,且GA-SVM模型预测精度明显高于BP和Elman网络。

图4 不同模型下预测值和实测值相对误差Fig.4 Relative errors of measured data and predict data of different models
三种模型预测性能结果对比见表3,用MSE、eMAPE和R三个指标进行预测性能评价。

表3 模型性能比较Tab.3 Comparison of model performance
从表 3可看出,GA-SVM 模型与 BP网络和Elman网络相比,GA-SVM模型的均方误差MSE和平均相对误差 eMAPE值分别为 1.68×10-4,6.42×10-3,远小于BP网络和Elman网络预测的相应指标值,且相关系数R为0.967,比BP网络和Elman网络模型的相关系数更接近 1,其预测结果精度更高,适应性更好,表明本文模型预测性能更优。这是因为在小样本情况下,神经网络是采用经验风险最小原则,而最小期望风险不能得到保证,同时神经网络优化过程只能保证收敛到某一个点,不能得到全局最优解。而GA-SVM模型则采用结构风险最小原则和VC维理论,在小样本下不仅最小化结构风险,还最小化 VC维的界,有效地缩小置信范围,从而达到期望风险最小,提高了模型的推广能力和精度,减少了依赖经验的程度;此外,GA-SVM模型通过对全局最优点求解,不存在困扰神经网络方法的易陷入局部极小值等问题,且训练样本特性通过利用RBF核函数来反映,从而使模型的鲁棒性和泛化能力变强。
6 结论
利用 GA和 SVM相结合建立了变压器绕组热点温度预测模型。在建模过程中,采用GA对SVM回归模型的惩罚因子C和核参数γ自动寻优选择,避免了人为主观经验地确定参数。通过输入变压器顶层油温、底层油温、油箱上死角温度、油箱下死角温度、环境温度和负载电流到模型中,对绕组热点温度进行预测的效果较好。与 BP模型和 Elman模型的相对误差对比分析表明,GA-SVM模型具有较好的泛化能力,为油浸式变压器绕组热点温度间接计算及预测辅助提出了一种新方法。
[1] 熊浩,陈伟根,杜林,等.基于T-S模型的电力变压器顶层油温预测研究[J].中国电机工程学报,2007,27(30): 15-19.Xiong Hao,Chen Weigen,Du Lin,et al.Study on prediction of top-oil temperature for power transformer based on T-S model[J].Proceedings of the CSEE,2007,27(30): 15-19.
[2] Tang W H,Wu Q H,Richardson Z J.A simplified transformer thermal model based on thermal-electric analogy[J].IEEE Transactions on Power Delivery,2004,19(3): 1112-1119.
[3] Chen W G,Pan C,Yun Y X.Power transformer top-oil temperature model based on thermal-electric analogy theory[J].European Transactions on Electrical Power,2009,19(3): 341-354.
[4] 滕黎,陈伟根,孙才新.油浸式电力变压器动态热路改进模型[J].电网技术,2012,36(4): 236-241.Teng Li,Chen Weigen,Sun Caixin.An improved dynamic thermal circuit model of oil-immersed power transformer[J].Power System Technology,2012,36(4): 236-241.
[5] IEEE.IEEE Std C57.91-1995 IEEE guide for loading mineral-oil-immersed transformers[S].Piscataway,NJ,USA: the Institute of Electrical and Electronics Engineers,1995.
[6] 中国国家标准化管理委员会.GB/T 15164—1994油浸式电力变压器负载导则[S].北京: 中国标准出版社,1994.
[7] Lesieutre B C,Hagman W H,Kirtley J L.An improved transformer top oil temperature model for use in an on-line monitoring and diagnostic system[J].IEEE Transactions on Power Delivery,1997,12(1):249-256.
[8] Swift G,Molinski T S,Lehn W.A fundamental approach to transformer thermal modeling - part I:theory and equivalent circuit[J].IEEE Transactions on Power Delivery,2001,16(2): 171-175.
[9] Susa D,Lehtonen M,Nordman H.Dynamic thermal modelling of power transformers[J].IEEE Transactions on Power Delivery,2005,20(1): 197-204.
[10] Pradhan M K,Ramu T S.Prediction of hottest spot temperature(HST) in power and station transformers[J].IEEE Transactions on Power Delivery,2003,18(4): 1275-1283.
[11] Galdi V,Ippolito L,Piccolo A,et al.Neural diagnostic system for transformer thermal overload protection[J].IEE Proceedings on Electric Power Applications,2000,147(5): 415-421.
[12] He Q,Si J N,Tylavsky D J.Prediction of top-oil temperature for transformers using neural networks[J].IEEE Transactions on Power Delivery,2000,15(4):1205-1211.
[13] Assuncao T,Silvino J L,Resende P.Transformer top-oil temperature modeling and simulation[J].Transactions on Engineering,Computing and Technology,2006,15(10): 240-245.
[14] Vapnik V N.The nature of statistical learning theory[M].New York: Springer,2000.
[15] 董明,孟源源,徐长响,等.基于支持向量机及油中溶解气体分析的大型电力变压器故障诊断模型研究[J].中国电机工程学报,2003,23(7): 88-92.Dong Ming,Meng Yuanyuan,Xu Changxiang,et al.Fault diagnosis model for power transformer based on support vector machine and dissolved gas analysis[J].Proceedings of the CSEE,2003,23(7): 88-92.
[16] 牛东晓,刘达,陈广娟,等.基于遗传优化的支持向量机小时负荷滚动预测[J].电工技术学报,2007,22(6): 148-153.Niu Dongxiao,Liu Da,Chen Guangjuan,et al.Support vector machine models optimized by genetic algorithm for hourly load rolling forecasting[J].Transactions of China Electrotechnical Society,2007,22(6): 148-153.
[17] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1): 32-42.Zhang Xuegong.Introduction to statistical learning theory and support vector machines[J].Acta Automatica Sinica,2000,26(1): 32-42.
[18] Keerthi S S,Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation,2003,15(7): 1667-1689.
[19] 王群京,鲍晓华,倪有源,等.基于支持向量机和遗传算法的爪极发电机建模及参数优化[J].电工技术学报,2006,21(4): 57-61.Wang Qunjing,Bao Xiaohua,Ni Youyuan,et al.Modeling and parameter optimization of the claw-pole alternator based on support vector machines and genetic algorithms[J].Transactions of China Electrotechnical Society,2006,21(4): 57-61.
[20] 王春林,周昊,李国能,等.基于支持向量机与遗传算法的灰熔点预测[J].中国电机工程学报,2007,27(8): 11-15.Wang Chunlin,Zhou hao,Li Guoneng,et al.Combining support vector machine and genetic algorithm to predict ash fusion temperature[J].Proceedings of the CSEE,2007,27(8): 11-15.
[21] Nguyen H,Baxter G W,Reznik L.Soft computing techniques to model the top-oil temperature of power transformers[C].International Conference on Intelligent Systems Applications to Power Systems(ISAP),Taiwan,2007: 1-6.
