基于PWM逆变器供电轴电流问题的交流电机耦合电容的计算与测量
2014-06-22刘瑞芳陈嘉垚马喜平程建全曹君慈
刘瑞芳 陈嘉垚 马喜平 程建全 曹君慈
(1.北京交通大学电气工程学院 北京 100044 2.福建省市力源电机有限公司 福安 355000)
1 引言
PWM 逆变器的使用大大提高了交流电机的性能,使得系统有良好的调速性能。但由于 IGBT等元件极高的开关频率,使得电机的轴承流过轴电流,危害轴承的寿命和电机的安全运行。这些PWM逆变器供电带来的负面影响逐渐被研究人员重视起来。
当电机采用变频供电方式时,逆变器中性点电压为

当电机为三相对称交流正弦供电时,该电压为0。而当电机由PWM逆变器供电时,中性点电压即共模电压不再为 0,而是随着开关器件的开通与关断而变化。在异步电机定子绕组、定子铁心及转子之间中存在着耦合电容。在正弦交流供电时这些电容不会对电机运行产生影响。逆变器供电时,在共模电压以及电机高频耦合电容作用下,在电机轴、轴承、以及电机机壳形成电气回路,将会产生共模电流。共模电流流过轴承,将会影响轴承的运行状态。轴电流局部放电能量释放产生的高温,可以融化轴承内圈、外圈或滚珠上许多微小区域,并形成凹槽,从而产生噪声、振动,若不能及时发现处理将导致轴承失效,对生产带来极大影响。据轴承制造商统计,25%的轴承损坏是因轴电压和轴电流造成的,而且这一比例正随 IGBT等高性能器件的广泛使用,而以惊人的速度增加。
对于变频供电下电机轴电流问题在国内外已经有很多学者进行了研究和探讨。对于轴电流问题的分析主要集中在以下两个方面:①轴电流的产生机理,轴电流通路的数学模型,以及各种参数对轴电流大小的影响;②轴电流的解决方案,如何减小和预防轴电流。对第一个问题即轴电流机理以及数学模型的准确把握是第二个问题即预防和减小轴电流的基础,非常重要。国外学者 Doyle Busse,Chen Shaotang,Annette Muetze等人进行了一系列的研究[1-8],分析了轴承电流的产生原因,确定共模电流所流经的电路,确定了所涉及到的电机高频参数,以及共模电路中的其他参数。其中,对于电机中的高频耦合参数,电机定子绕组对定子铁心的耦合电容、电机定子绕组对转子的耦合电容、转子对定子铁心的耦合电容等根据电机结构给出了解析计算公式,并通过与测试结果对比参数的可靠性。国内学者万健如,黄立培,王世怀等人的研究也主要集中在轴电流模型和各种参数对轴电流的影响,所采用的研究方法与国外学者的相近[9-13]。轴电流的抑制和预防是研究者们关注的另一个问题。目前所提出的防范措施包括采用正弦波滤波器、电机转轴系统接地、对轴承和轴颈进行绝缘、采用陶瓷轴承,采用法拉第屏蔽层、加共模扼流圈以及美国 AEGIS公司提出的依据静电放电机理而设计的轴承保护环[14]等。
在轴电流问题的研究中,还有如下问题没有得到很好的解决。
(1)在现有文献中,所研究的电机容量从小电机如 1kW,到大电机如 500kW 都有涉及。实际应用中,不同容量的电机其轴电流问题的严重程度也不同。因此有必要从系列电机的角度进行研究,探究轴电流模型中的不同容量电机的耦合电容参数变化规律与轴电压、轴电流的关系。
(2)电机耦合电容参数的准确性决定了轴电压的计算的准确,继而决定了轴电流的准确性。电机的耦合电容不易直接通过测量得到。电机在静止时,在重力作用下轴承的内外圈与滚珠之间存在金属性接触,使得转轴与定子机座导通,无法分离出电机的各个电容来。如果能够根据电机的型号规格和设计尺寸得出电容参数,将对问题的分析带来很大的便利。在以往的研究中对电机耦合电容的计算都是基于解析公式,有许多简化和假设。实际应用中,不同容量交流电机结构不同,电机的定子,转子槽形多样,这些都会影响耦合电容参数的大小。更加可信和实用的计算方法是对针对不同电机进行电磁场有限元数值计算获得耦合电容参数计算。电磁场数值计算,可以对各类结构的电机进行分析,不需要进行太多的假设,所得的结论也更为接近实际问题。
本文将对一系列异步电机的耦合电容进行分析,将有限元电磁场计算结果与简单解析公式的结果进行分析比较。并设计一种电容的测试方法,对解析计算模型以及有限元计算模型的计算结果进行分析和比较。
2 异步电机中的耦合电容
在异步电动机中,定子绕组分布在电动机定子槽内,中小型电机定子绕组是由聚酯亚胺漆包圆铜线组成,由槽绝缘将定子绕组与定子槽隔开,定子铁心与转子之间通过气隙隔开,定子绕组与转子之间存在槽楔和空气隙。小功率异步电动机转子为笼型转子,电动机转轴与转子铁心相连,电位相同,定子铁心安装在机座内。轴承外圈与定子端盖相接,轴承内圈与转轴相接,如图1所示。
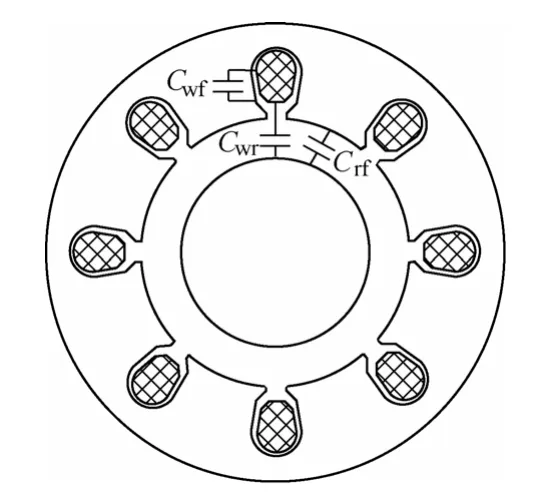
图1 异步电动机结构Fig.1 The structure of the induction motor
在电机中存在下面一些耦合电容:
(1)定子绕组与定子铁心之间的耦合电容Cwf。定子绕组与定子铁心之间有槽绝缘,将绕组和定子铁心视为两个电极,定子绕组与铁心之间存在耦合电容Cwf。
(2)定子绕组与转子之间的耦合电容 Cwr。定子绕组与转子之间的电容 Cwr是由转子表面与定子绕组之间的绕组绝缘、槽楔、槽绝缘和气隙组成的间隙产生的。
(3)转子与定子铁心之间的耦合电容Crf。转子对定子铁心电容 Crf是由转子表面和定子铁心表面之间的气隙部分决定的。
(4)轴承电容Cb。电机两端有轴承,在轴承润滑膜完整,即轴承的润滑膜具有绝缘性能时,轴承可等效为电容Cb。其大小与润滑油脂粘度、温度、几何结构、介电常数、载荷,以及转子的转速等参数有关。
在 PWM变频供电时,电机定子绕组中性点电压vn不为零。定子绕组与机壳、定子绕组与转子、转子与定子铁心以及轴承的电容 Cwf,Cwr,Crf和Cb形成电容网络,如图2所示。

图2 驱动系统共模通路的等效电路Fig.2 Equivalent circuit of common mode current in drive system
轴承对地电压vb与电动机共模电压vn之比定义为轴承电压比[1](Bearing Voltage Ratio,BVR)

由此可以看出,轴承电压比与异步电机耦合电容存在着密切的关系。要准确预测轴电压的大小,需要确定上面公式中的各项电容参数。
对电机电容的计算方法有解析法和数值计算两种方法。下面先介绍基于解析法的电容计算。
3 电机耦合电容的解析计算
当已知电机结构参数时,可对电机进行耦合电容的解析计算。本文将在文献[1,6]研究的基础上,分析电机容量对电容参数的影响。
3.1 定子绕组到定子铁心之间的电容Cwf
忽略定子绕组导线漆包线的绝缘时,假设绕组为铜导体充满了槽内空间,它和定子铁心间的电容视为平板电容,导出Cwf的计算公式为

式中,Ns——电机定子槽数;
εr——槽绝缘的相对介电常数;
ε0——真空介电常数;
g0——槽绝缘厚度;
Ls——定子铁心有效长度;
W——定子绕组和定子铁心之间槽绝缘的有效弧长。
从式(2)可知,该电容与轴电压分压比没有直接关系,但是从图2可以看出它会影响总共模电流的大小。
3.2 定子绕组到转子之间的电容Cwr
在不考虑其他导体的存在情况下,近似将这两等效电极构成的电容按平板电容来处理。其基本结构为定子绕组-盖槽绝缘-槽楔-空气-转子。定子绕组到转子之间的电容等效为有三种不同介质平板电容的串联。设盖槽绝缘的相对介电常数为εr1,厚度为d1;槽楔的相对介电常数为εr2,厚度为 d2;气隙的长度为δ;槽楔正对转子一侧的面积为S,则定子绕组到转子之间的电容Cwr为

3.3 转子与定子铁心之间的电容Crf
由于转子导条和转子铁心都是导体,计算转子与定子铁心电容时可以将转子导条和转子铁心视为一个电极,因此可以不考虑转子齿槽的影响。而定子铁心槽内放置了与之绝缘的定子绕组,因此定子开槽影响着分布电容。为了计算开槽对电机的影响,可以引入卡式系数来考虑。定子开槽使得有效气隙增大,等效的气隙为δ′,δ′=kcδ,(kc≥1),kc为卡氏系数,δ 为电机实际气隙长度。等效定子和转子之间的电容可视为两同轴圆柱电极的电容,电极之间的距离为kcδ,所以通过式(5)进行计算
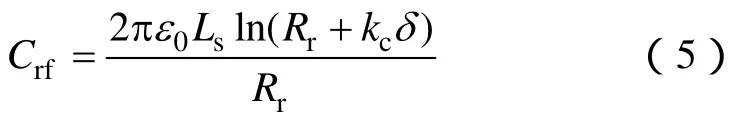
式中 Rr——转子外圆半径。
轴承电容的解析分析参见文献[17]。
3.4 电机耦合电容解析计算结果的分析
通过上述的解析公式,并结合《Y2系列(IP54)三相异步电动机技术数据(380V、50Hz)》对不同功率的异步电动机耦合电容进行计算。假设[1]Cb=Cwr根据式(2)计算BVR。本文选取了极数为4的五种不同额定功率的异步电动机进行了解析计算,经过计算整理后得到的结果见表1。

表1 五种电机电容的解析计算结果Tab.1 Analysis calculation results of five types of induction motor
分析表 1,三种电容参数都随着机座号的增大而增大。轴承分压比 BVR都在 10%之内。通过这个数值可以预估出轴电压的大致范围。BVR的值随着电机容量的增加而增大,如图5所示。意味着,当变频器有相同的共模电压时,大功率电机的轴承电压相对较大。从三个电容对轴电压分压比 BVR的影响来分析,分子上电容 Cwr,数值较小;分母的三个电容中,电容 Crf远大于其他两个电容,占主要部分。

图3 电机容量对BVR值的影响Fig.3 Influence of motor capacity on BVR
4 耦合电容的有限元计算
解析计算的优势是简单、方便、计算量小。在文献[1]对电容解析计算与测量结果进行比较,发现计算结果并不令人满意,甚至指出由于电机结构复杂,准确计算出电机的电容是不可能的。下面本文将探讨用有限元法计算耦合电容的计算模型。
在解析计算中,将电机的耦合电容视为三个独立存在的电容。而实际上定子绕组、定子铁心和转子三个部分形成一个多导体静电独立系统,它们之间互相影响,应当按照部分电容的理论进行分析。
根据部分电容理论,对于三个及三个以上带电导体组成的系统来说,任意两个导体间的电压不仅要受到它们自身电荷的影响,还要受到其他导体上电荷的影响,这时,系统中导体间的电压与导体电荷间的关系可用部分电容来描述。在n+1个导体构成的静电独立系统中,共应有n(n+1)/2个部分电容。这些电容构成一个电容网络,把场的概念和路的概念联系起来了。在图4所示的静电系统中,n=3,共有6个部分电容。
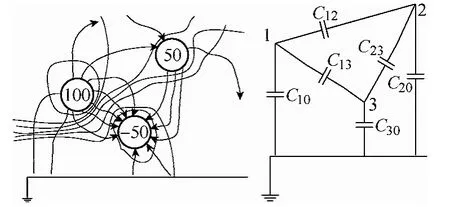
图4 部分电容与电容网络Fig.4 Partial capacitor and capacitor net
电机的结构如图5所示,当将定子机壳(包括定子铁心)视为参考电极时,定子绕组和转子为两个独立导体,则共有三个部分电容。采用电磁场有限元方法可以计算它们之间的部分电容。忽略端部影响时,可以采用 2D建模分析。应用 ANSYS Maxwell的静电场求解器中进行分析,将定子机壳视为参考电极,给定子绕组和转子施加电压激励,求解电位φ 满足的静电场泊松方程

图5 电容矩阵结构Fig.5 Capacitance matrix structure

通过计算静电储能,可以获得三个部分电容。
4.1 有限元计算模型
根据电机结构的对称性,仅需要对一个槽距范围进行建模分析。在转子部分因为对于铸铝转子导体与铁心均为导体,在静电计算中均按导体来处理,转子开槽对电场计算无影响。因此可以将转子用光滑导体来处理。
对于Y2-100L1-4电动机进行建模。该电机为定子36槽,槽楔厚度为2mm,槽楔采用型号为3 240的环氧酚醛层压玻璃布板,相对介电常数2.25。槽绝缘为 0.25mm,相对介电常数为 2.25。本文先按照实心导体模型进行了计算,如图6所示。采用本文第5节部分的测试方法进行电容的测试。将计算结果与实验测试结果对比,见表 2。发现计算电容值与测量值存在较大差异,尤其是Cwf的值相差较大。

图6 实心导体模型Fig.6 Solid conductor model
对此进行分析,实心导体模型相当于槽满率为100%,与实际情况不符,实际导线并未充满槽内空间,散电磁线外面有漆膜。将槽内导体部分材料全部设为铜,会凭空增大槽内金属导体的区域,相当于增大了电极的相对面积,会使得 Cwf增大。这种模型误差带来了电容参数计算结果的误差。在计算磁场时不需要考虑散线结构,但是在电场分析时,必须考虑散线分布情况。
该电机每个定子槽中有44根线径为0.67mm和44根线径为0.71mm的导线组成。漆膜为聚酯亚胺,漆膜双面厚度为0.06mm,相对介电常数为3.2。槽内其余空间充满绝缘漆。散电磁线绕组几何模型如图7所示。
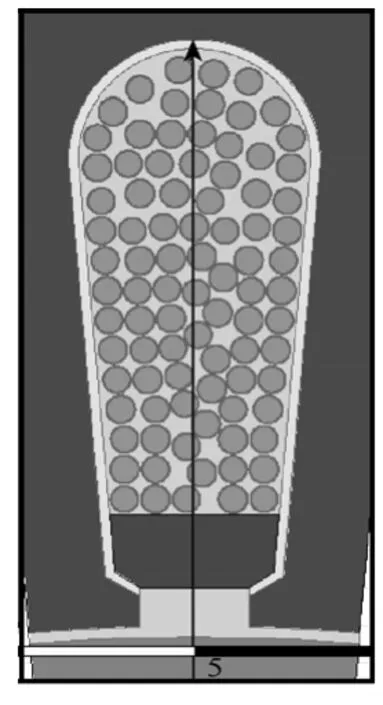
图7 散线模型Fig.7 Scattered line model
对实心导体模型和散线模型的电机电容有限元计算结果和解析法以及测量结果进行比较见表2。

表2 耦合电容计算结果与测量值比较Tab.2 Coupled capacitances results from measured and calculation
从计算结果来看,解析法与实心导体有限元模型的 Cwf接近,与实测值相比误差在 80%以上,而散线有限元模型与测量结果比较,减小到9.2%。因为解析法和集中导体模型都没有考虑槽内绕组的实际分布而产生了模型上的误差。如果要得到比较准确的结果,必须考虑绕组的实际结构。精确计算Cwf对准确预测电机的对地漏电流非常重要。另外两个电容Cwr和Crf,有限元两种模型计算结果较为接近。从电机结构来分析,散导线还是集中导线对 Cwr和Crf不大。转子到机壳电容 Crf,解析计算与有限元法的结果比较接近,都小于测试值。
4.2 绕组端部对耦合电容Cwr的影响
从表 2可以看出,定子绕组到转子电容 Cwr有限元计算结果仅为测试结果的50%,有较大偏差。对电机模型进行分析,误差产生的主要原因来自电机绕组端部。由于定子绕组端部伸出铁心外,转子存在端环,定子绕组和转子两电极之间的耦合面积要大于 2D有限元法中假定的定子铁心长度范围内的面积。电容与电极的面积乘正比,因此实际 Cwr比2D有限元计算结果大。在ANSYS中建立了感应电机三维几何模型如图8所示,其中定、转子铁心长 90mm,定子绕组端部伸出铁心的直线部分为15mm,端部曲线部分投影长26.8mm,笼型端环轴向厚度为 11mm,端环径向高度为 20mm。为突出端部起见,未显示机壳、转轴及轴承。

图8 感应电动机三维模型Fig.8 3D model of induction motor
对耦合电容 Cwr的计算结果和测量结果进行比较,见表3。

表3 耦合电容Cwr计算值与实测值比较Tab.3 Calculating and measured results of coupled capacitance Cwr
由表 3可知,与实测值相比,Cwr的计算值由2D的10.9pF变为3D的20.3pF,误差由2D模型的50%减小到3D的6%,考虑端部大大提高了Cwr的计算准确度。所以为了获得准确对转子与定子绕组之间的耦合电容,必须考虑定转子绕组的端部的影响。
4.3 散电磁线随机分布对耦合电容影响
虽然电机定子绕组散线模型提高了计算的精确度,但由于定子槽内定子绕组导体分布是随机的,导体分布可能会对结果造成一定影响。因此对Y2-100L1-4机型的异步电动机在随机三种不同导体分布下进行了建模和计算,来分析导体随机分布对电机电容参数的影响。在实际电机中,每一个电磁线的位置市不确定的,同一电机的不同槽内绕组分布也不会完全一致。因此建模时,对散导线放置并未设置特定的规则。只是令其大致均匀的分布在槽内。图9为三个随机分布定子散线的几何模型。
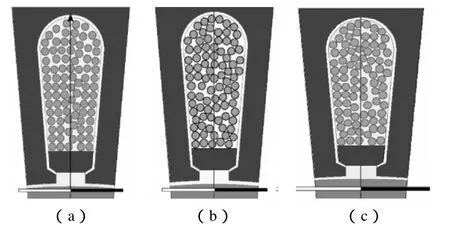
图9 散电磁线随机分布的三个模型Fig.9 3 models of scattered lines in random distribution
将上面的计算结果进行整理见表4。

表4 电磁线随机分布对电容的影响Tab.4 Capacitance under random distribution of scattered line
对表4的数据进行分析,发现随着定子绕组在定子槽内分布的不同,会对各个电容值带来一定的影响,但影响不大。对 Cwf的影响,以平均值为基准浮动范围在1%之内。
5 电机耦合电容的测量
为了验证计算方法和计算结果的正确性,需要对电机内部的高频耦合电容进行实际的测量,电机处于静止状态时,在重力作用下轴承内外圈与滚珠接触,使得定、转子在电气上是导通的。因此无法直接测量。文献[1]介绍了采用绝缘轴承大容量电机的耦合电容测量方法以及绝缘了轴承座的试验样机的耦合电容测试。但是对于普通的电机既没有采用绝缘轴承,轴承座也未绝缘,所提的方法没有办法实施。下面介绍一种用塑料轴承替代实际轴承测量电机耦合电容的方法。
先将转子从电机中取出,卸下金属轴承,用同样型号塑料轴承代替实际的电机轴承,安装到电机转轴两端,再重新装回电机机座内。这样就使得电机机座和转轴之间没有金属接触。实验样机 Y2-100L1-4两端的轴承均为深沟球轴承,型号均为6206,图10为6206金属轴承和塑料轴承。塑料轴承的内外圈均为塑料,滚子材料为玻璃。图11为已经装好白色塑料轴承的电机转子。本文采用安捷伦LCR测试仪U1733C的电容档进行测量。

图10 金属轴承和塑料轴承Fig.10 A metal bearing and aplastic bearing

图11 用塑料轴承替换原有轴承Fig.11 Substituting plastic bearing for actual bearing
测量原理图如图12所示,图中Cp为塑料轴承对应的电容。采用塑料轴承后,定、转子电气隔离。为了考虑塑料轴承带来的影响,需要在测量中计入塑料轴承电容。Cp可以通过轴外径和轴承座内径所等效的圆柱形电容计算得到。

图12 电容测量原理示意图Fig.12 Capacitance measuring models
为方便表述,令
测量方法如下:
(1)使用电容表的负端碰触机座导电部分,正端分别碰触接线盒中 U1,V1,W1相,测得 3组数据 C′11,C′12,C′13,取平均值 C1。
(2)使用电容表的负端碰触转轴,正端分别碰触接线盒中的U1,V1,W1相,测得3组数据C′21,C′22,C′23,取平均值 C2。
(3)使用电容表的负端碰触机壳导电部分,正端碰触转轴,测得C3。
其中

用 C1,C2,C3可计算出 Cwf,Cwr,C′rf,再由式(7)可以求出Crf。
6 结论
变频驱动给电机运行带来轴承电腐蚀加剧的问题。为了准确预测电机轴电流,以及研究有效的抑制措施,对电机耦合电容参数进行准确计算和测量有重要意义。本文对文献中耦合电容参数的解析计算法进行了梳理,分析了电机容量对轴承分压比的影响,得到结论随着电机额定功率的增大,轴承的分压比也会增大。采用有限元法对耦合电容参数进行了求解,针对实心导线模型带来的误差,提出了定子绕组电磁散线计算模型,新模型使得定子绕组对机座的电容 Cwf精确度大大提高。而三维有限元分析表明电机端部对定子绕组与转子的耦合电容Cwr有很大影响。为了验证计算分析的正确性,设计采用塑料轴承替代实际轴承的耦合电容测试方案。由于电机轴承的装卸需要专用的工装,需要在电机厂进行。由于大电机难以找到同样型号的塑料轴承,本文的测试方法仅适用于小容量电机。
[1] Muetze A,Andreas Binder.Calculation of motor capacitances for prediction of the voltage across the bearings in machines of inverter-based drive systems[J].IEEE Transactions on Industry Applications,2007,43(3): 665-672.
[2] Muetze A,Tamminen J,Ahola J.Influence of motor operating parameters on discharge bearing current activity[C].Energy Conversion Congress and Exposition(ECCE),2010: 2739-2746.
[3] Magdun O,Binder A.Calculation of roller and ball bearing capacitances and prediction of EDM currents[C].35th Annual Conference of IEEE on Industrial Electronics,2009: 1051-1056.
[4] David Hyypio.Mitigation of bearing electro-erosion of inverter-fed motors through passive common-mode voltage suppression[J].IEEE Transactions on Industry Applications,2005,41(2): 576-584.
[5] Busse D,Erdman J,Kerkman R,et al.Systemelectrical parameters and their influence effect on bearing currents[J].IEEE Transactions on Industry Applications,1997,33(2): 577-584.
[6] Rajendra N,Thomas A,Nondahl,Michael J,et al.Circuit model for shaft voltage prediction in induction motors fed by PWM-based AC drives[J].IEEE Transactions on Industry Applications,2003,39(5):1294-1299.
[7] Doyle Busse,Jay Erdman,Russel J Kerkman,et al.Bearing currents and their relationship to PWM drives[J].IEEE Transactionson Power Electronics,1997,12(2): 243-252.
[8] Chen S,LipoT A,Fitzgerald D.Modeling of bearing currents in inverter drives[J].IEEE Transactions on Industry Applications,1995,32(6): 1365-1370.
[9] 万健如,禹华军.变频电机轴承失效机理分析[J].轴承,2002(8): 24-27.Wan Jianru,Yu Huajun.Failure mechanism of motor bearings in the frequency conversion driving system[J].Bearing,2002(8): 24-27.
[10] 黄立培,浦志勇.大容量 PWM 逆变器对交流电机的轴电压和轴承电流的影响[J].电工电能新技术,2000(4): 39-43.Huang Lipei,Pu Zhiyong.Effects of large capacity PWM inverter on AC motor bearing currents and shaft voltages[J].Advanced Technology of Electrical Engineering and Energy,2000(4): 39-43.
[11] 幸善成,吴正国.逆变器驱动电机系统环路型电机轴承电流的研究[J].海军工程大学学报,2006,18(2): 64-68.Xing Shancheng,Wu Zhengguo.Circulating type motor bearing current in PWM inverter drives[J].Journal of Naval University of Engineering,2006,18(2): 64-68.
[12] 刘欣,孙力,孙亚秀.PWM驱动系统中感应电动机轴电压轴电流研究[J].微电机,2007(9): 5-8.Liu Xin,Sun Li,Sun Yaxiu.Research on induction motor shaft voltage and shaft current in PWM drive system[J].Micromotors Servo Technique,2007(9):5-8.
[13] 王世怀,熊万里,段志善.PWM变频调速电机轴承电磁损伤的机理研究[J].电力科学与工程,2004(3):5-8.Wang Shihuai,XiongWanli,Duan Zhishan.Investigation on motor bearing electromagnetism damage induced by PWM inverters[J].Electric Power Science and Engineering,2004(3): 5-8.
[14] Muetze A,Oh H W.Application of static charge dissipation to mitigate electric discharge bearing currents[J].IEEE Transactions on Industry Applications,2008,44(1): 135-143.
