现代计量经济学中的非均值模型：一个方法论角度的理论综述

金玉国 金 戈

(山东财经大学统计学院，山东 济南 250014)

一、引言

计量经济模型是反映社会经济现象之间的数量依存关系的数学模型，用于度量一个或一组变量(解释变量或自变量向量，记为x)对被研究的社会经济现象(被解释变量或因变量向量，记为y)的某种统计分布特征的影响，如边际效应、乘数、弹性系数等。社会经济现象的统计分布特征可以从不同侧面进行反映和度量，如均值、方差、分位数、条件分布等。按照模型反映的分布特征类型，可将计量经济模型分为条件均值模型和非均值模型两大类。

条件均值模型是计量经济模型的最基本模型形式，因变量是被研究事物的条件均值，一般形式为E(y|x)=xβ，或等价的随机形式：y=xβ+u(u是随机误差项)。回归系数向量β表示y的条件均值对各解释变量向量x变动的平均响应。条件均值模型应用非常广泛，但也存在较大的局限性：一方面，只能度量自变量对因变量条件均值的边际效应，不能度量自变量对因变量分布的其他特征(如方差特征、分位数特征等)的边际效应；另一方面，模型的假定过于严格，如随机误差项u需满足同独立同分布、零均值、同方差性等条件，现实经济数据往往很难完全满足这些条件，限制了模型的适用性。为了弥补均值模型的缺陷，到20世纪七八十年代，计量经济模型在传统的均值模型基础上，开始不断向非均值模型拓展。

非均值模型关注的是变量的除条件均值以外的其他分布特征，如条件分位数、条件方差、条件概率等，根据反映的特征，产生了相应的非均值模型，如分位数模型、方差模型、概率模型等。所以非均值模型是一个统称，即一个“模型族(Models Family)”。非均值模型建模方法论突破传统计量经济学建模方法的局限，既是均值模型建模方法论的发展和延伸，又在模型设定、建模假定、估计方法、模型评价和模型应用等方面有着很大的不同，极大地丰富了计量经济建模方法论的理论体系。

非均值模型建模方法论的出现引起了理论界的重视。早在1998年，K.Dotes就断言，非均值模型的发展正在形成一种与传统建模方法分庭抗礼的建模方法论。其后，D.Hallas(2005)从理论角度对部分非均值模型(方差模型、分位数模型)的建模方法进行了归纳，并分析了非均值模型建模方法对传统计量经济学建模方法论的冲击；K.Ginges、R. Donald(2010)分析了非均值模型在金融市场研究领域应用的特点和对其他领域的影响。金玉国(2011)则看重这种建模方法的内在一致性，将几种常见的非均值模型归为非经典计量经济模型的一个大类(其他还包括特殊数据模型、潜变量模型、非固定参数模型)，并简单了分析了与经典计量经济学建模方法的不同之处。

尽管学术界对非均值模型有了一些研究，但大部分是针对某些特定模型的研究，从系统(或整体)角度对非均值模型建模方法论的研究还非常少见，对其建模理论和方法发展演化的规律性缺乏必要的归纳和梳理。有鉴于此，本文拟将非均值模型作为一个整体进行系统研究。本文的研究思路如下，首先，划分非均值模型的基本类型，回顾各种模型的产生与发展历史、应用领域及建模原理；其次，对各类非均值模型建模方法论进行简要归纳；最后，总结非均值模型建模方法论的特点，并与均值模型建模方法论进行比较。

二、非均值模型的基本分类

目前比较成熟的非均值模型包括以下四个基本类型：条件分位数模型、方差模型、概率模型(包括离散选择模型、持续时间模型)和分布函数模型。

(一)条件分位数模型

传统的条件均值模型反映的是自变量对因变量的条件均值的边际效应或乘数(如果变量为对数形式，则为弹性系数或半弹性系数)，其假设是不同分布点上边际效应或乘数是相同的，所以不能反映分布的细部特征。而且这个假定往往是不合理的，尤其是因变量数据分布偏态时更是如此。而条件分位数模型的出现，在很大程度上弥补了条件均值模型的上述缺陷。

分位数模型起源于18世纪中后期Bosccovich、Edgeworth对中位数线性回归问题的研究。由于中位数其实是分位数的一个特例，所以他们的研究为分位数模型的发展奠定了基础。1978年，Koenker 和Bassett系统地提出线性分位数回归模型的理论。

分位数模型关注的是因变量的条件分位数，是指因变量的条件分位数与自变量建立的回归模型，其目的是观察分布中不同分位点上解释变量对被解释变量的不同边际效应。基本形式为：

yi=xiβτ+ετi其中， yi为被解释变量，xi是k维行向量，表示k个解释变量中第i个观察值，βτ是k维列向量，分别表示对应于被解释变量第τ分位数的各解释变量的回归系数，εθi是符合有关古典假定的随机误差项。给定解释变量x时，被解释变量y的第τ个条件分位数为Qτ(yi|xi)=xiβτ。参数βτ在被解释变量的条件分布中的不同分布点之间可以是不同的，相当于给定几个分位点，就有几个对应的回归方程。因此，分位数回归模型可以反映出位置情况和分布形状，对变量之间的结构关系进行更详细的特征描述。所以，分位数模型是对是均值模型的细部化，目前分位数模型已发展成为描述样本分布细部特征的有力工具，被广泛应用于经济、教育、环境科学、医学等领域。

(二)条件方差模型

对有些经济问题，传统的经济计量模型——条件均值模型无法反映事物之间的联系。以金融市场为例，根据有效市场假说，条件均值模型对金融产品的价格走势没有预测效果。而且条件均值模型往往假定方差不变，但金融市场的波动受到政局、消息、政策等因素的影响，往往呈现“波动聚集性”。实际上，由于市场波动性和收益性之间存在联系，我们更加关注的是市场的波动问题。而变量的波动性，可以用方差反映出来，所以，条件方差模型应运而生，被广泛应用于具有波动集聚性的时间序列数据建模。方差模型主要包括自回归条件异方差模型(ARCH族模型)和随机波动模型，其中，尤以ARCH族模型应用最广。一般ARCH模型的基本形式如下：

(1)

(2)

由此可见，条件方差模型把当期随机项的方差假定为以前各期误差项平方的线性函数，描述了随机项的方差的“记忆性”特征，与均值模型结合起来，有助于全方位的反映变量的波动规律。

继Engle后，很多学者从不同的角度推广了ARCH模型，进一步拓展了ARCH模型的应用领域，产生了所谓的“ARCH族模型”，包括GARCH( Bollerslev，1986)、ARCH-M (Engle，Lilien，Robbins，1987)、TARCH(Zakoizn，1990)、EGARCH (Nelson，1991)等一系列条件方差模型。

条件方差模型可以很好的刻画随机变量波动的集群性和方差的时变性，尤其是刻画金融时间序列数据的波动性，所以不但应用于金融市场的期货交易、风险控制、投资组合风险管理策略等领域，还被广泛应用于与波动性有关的经济理论验证、政策研究及季节性分析等领域。

(三)条件概率模型

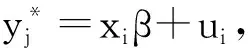
其中F(·)是随机误差项u的分布函数，原则上，任何适当的、连续的、定义在实轴上的概率分布函数都可以选用。对于连续随机变量来说，概率密度函数的积分代表概率的大小，也就是说，连续随机变量的(累积)分布函数(CDF)都可以满足因变量值域为[0,1]的要求。在实际建模过程中，F(·)通常选用Logistic分布函数和正态分布的累积分布函数，分别生成了Logit和Probit模型，这就是最基本的条件概率模型。

条件概率模型包括离散选择模型(二元选择模型、多元排序选择模型、无序选择模型等)和持续时间模型。前者研究的是自变量对某一随机事件发生的概率的边际效应；后者研究的是自变量对某活动持续时间长度的概率的边际效应，但二者的因变量都是随机变量的概率特征。条件概率模型的估计方法和应用研究主要发展于1960-1970年代，经过Marchark、Marley和McFadden等人的发展，目前已经成为微观计量经济学的主要方法之一。

(四)分布函数模型

分布函数模型的建模对象是概率分布函数，主要用于分析变量间相关结构。目前最为典型的分布函数模型是Copula函数模型，它是一种将联合分布与它的边缘分布连接在一起的函数。Copula理论由统计学家Sklar于 1959年最早提出，随后Genest和Mackay(1986)、Joe(1993)将Copula理论进一步发展，使其成为构造多元联合分布和分析多变量间相关结构的重要工具。基本思想是：

对于具有边缘分布F1(x1),…,FN(xN)的联合分布函数F，如果存在一个函数C，满足:

F(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN))

则称C(·)为Copula函数。Copula函数其实就是一个边缘分布到联合分布的映射。其应用意义在于， Copula密度函数实际上表示了各变量之间的相关结构，不仅是构建多维分布的工具，同时也是研究随机变量之间相依结构的工具，用Copula模型可以测得两者之间的相关关系及尾部相关性，对此均值模型无能为力。Copula函数与GARCH模型、极值理论等结合，发展出了一些新的模型，而且研究还在深入。这种模型目前不但被普遍用于金融领域的计量研究，而且在保险、生物统计学、气象、地质地质、海洋等领域都有所应用。

三、非均值模型建模方法论

(一)条件分位数模型

相对于传统的均值模型中，分位数模型中的参数估计、显著性假设检验以及模型拟合优度检验方法要复杂得多。目前，分位数模型大致可以分为参数模型、非参数模型、半参数模型这三类，每种模型都有其各自的估计方法。我们仅以参数模型为例加以说明。

一般的分位数回归模型形式为：

yi=xiβτ+ετi

参数估计一般采用最小二乘法，即加权绝对离差最小(Weighted Least Absolute，WLA)准则，其表达式为：

上述参数估计方法称为最小绝对离差法(LAD)。这种方法对模型中的随机扰动项不需做任何分布的假定，参数估计量具有稳健性、耐干扰性和良好的渐进性质。

分位数模型的参数显著性检验一般采用Tw(τ) 和TL R(τ)统计量。二者在原假设下都服从χ2(q)。Koenker 与Machado (1999)还依据均值模型中拟合优度R2的计算思想，基于残差绝对值的加权和，设计了分位数模型拟合优度的计算方法，用于度量在某个具体的分位点(τ)下模型的拟合效果。

(二)方差模型

ARCH模型常用的估计方法是极大似然估计(Maximum Likelihood，ML)方法。下面以最简单的ARCH模型为例，说明其建模方法。

假定均值模型是：

yt=xtβ+ut

其中 β= (β0β1, …, βk-1)′, xt= (1 x1, …, xk -1)(xt的分量也可以包括yt的滞后变量)，假定估计参数所用的时间序列长度(样本容量)为T。如果假定ut～ARCH (q)，可以记为：

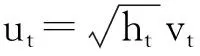
其中，vt| xt～i.i.d(0,1)，ht= α0+α1ut -12+α2ut -22+ … + αqut-q2。所以有σt2=E(ut2)=ht，E(ut) = 0。假定yt服从正态分布，概率密度函数为

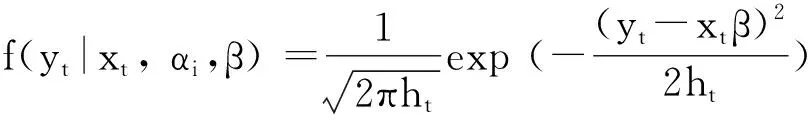
据此，构造对数似然函数：

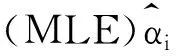
(三)条件概率模型

在条件概率模型建模过程中，极大似然估计(ML)方法是估计参数的最常用方法。下面以二元选择模型中的Logit模型为例介绍概率模型的建模原理。

对于Logit模型的一般形式为：

对于给定的xi，E(y|xi)表示y=1的条件概率pi，相应地， y=0的条件概率是(1-pi)。所以有：

但在样本中，pi的信息是观测不到的。我们只能得到对于xi的既定值，因变量yi取值为0或1的信息。极大似然估计的思路就是以样本观测值最有可能发生为条件，利用多元函数极值原理求得系数β的估计值。在样本中，如果被观察到了n次，y=0被观察到了N-n次，则似然函数是

以使其最大化为条件，便可求到参数向量β的极大似然估计值。对概率模型的检验可以采用基于ML的一系列χ2检验。

(四)概率分布函数模型

建立Copula函数模型的主要问题为确认各变量的边缘分布和找到合适的Copula函数表达变量之间的相关结构。Copula函数的构造方法较多，比较常见的Copula函数主要分为三类：椭圆型Copula(如正态Copula 函数，Student-t Copula 函数)，阿基米德型(如Gumbel-Copula函数、Frank-Copula函数)以及极值型(Galambos-Copula函数)。

Copula模型的参数估计方法可以分为参数方法和非参数方法，最常用的方法大都基于极大似然估计法，比如完全极大似然估计法、两阶段极大似然估计法、伪极大似然估计法等。运用Copula函数建模过程中的关键一步就是选择最优的Copula函数，这是国内外学术界的研究热点，但仍没有被广为接受的检验方法，常用的有图形诊断法、拟合优度检验(包括AIC、SC、χ2检验、K-S检验等)。

四、非均值模型建模方法论特点及其对计量经济学发展的影响

为了更加清楚地反映非均值模型建模方法的论特点，可以将各类计量经济学建模方法论的特点归纳如下表：

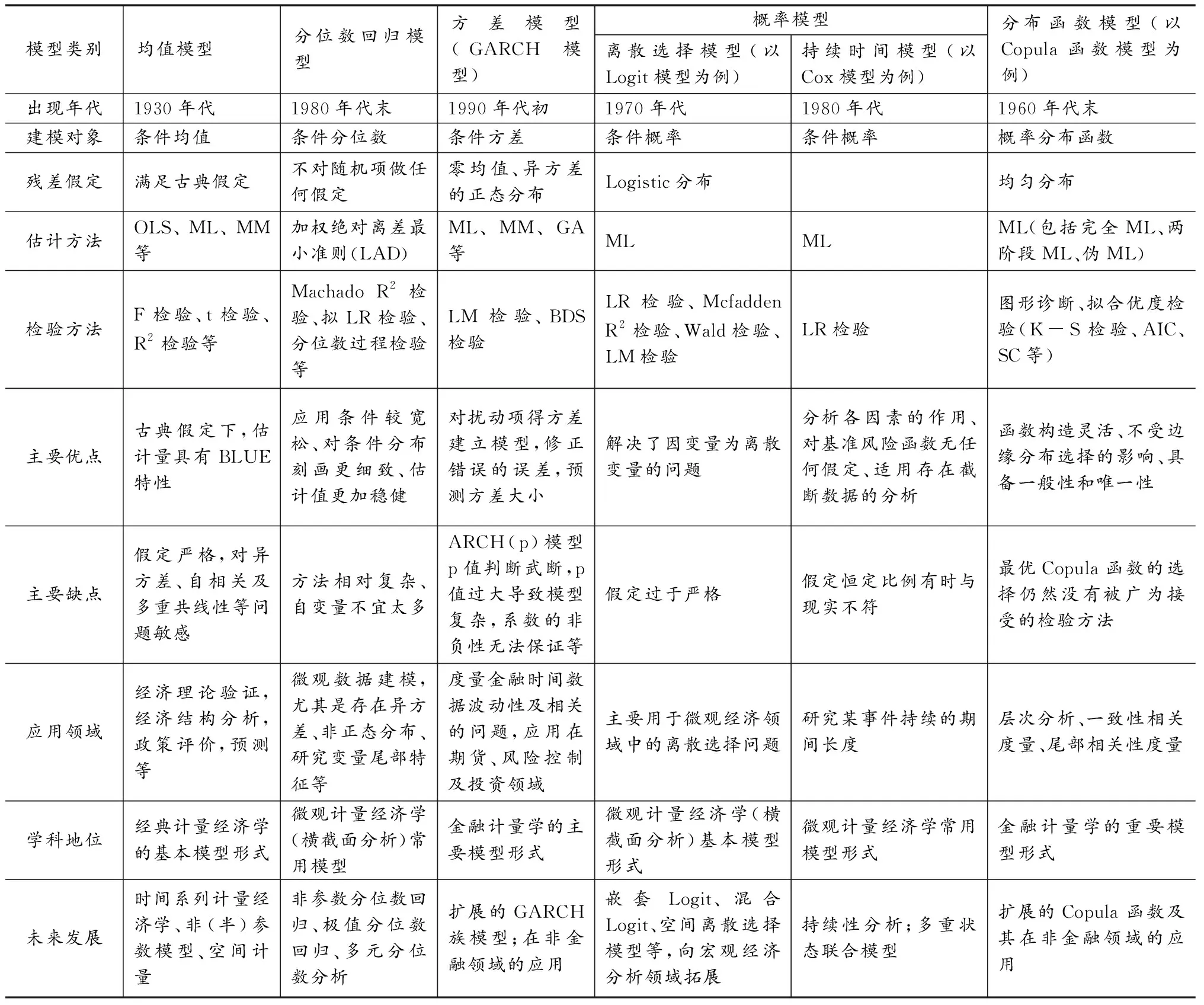
表1 各类计量经济学建模方法论的特点比较

由此可见，各类非均值模型的特点不同，但他们之间又相互联系和渗透。非均值模型的出现，拓展了计量经济学的研究范围，丰富了计量经济学的建模方法论，为经济问题的实证研究提高了更加有效的工具和更为适用的方法。非均值模型建模方法论对计量经济学发展的影响具体体现在以下四个方面：

1.非均值模型建模对象更复杂多样。如分位数回归将唯一的的条件均值回归，扩展到任意分位数；ARCH模型将建模对象扩展为方差(波动)特征；离散选择模型和持续时间模型的建模对象为概率；分布函数模型将研究对象扩展到概率分布函数。因此，只要现实经济问题对建模方法提出了新的要求，现代计量经济学都能提供有效的工具和科学的方法，体现了其较强的包容性和“弹性”特征。

2. 非均值模型随机项的假定更灵活。为了进行统计推论，传统的均值模型要满足经典线性模型假定(古典假定)，而分位数回归不做任何假定，其他非均值模型中有的只是假定服从正态分布，有的还扩展到Logistic分布等。模型假定的“松动”，有助于克服传统计量经济模型的局限性，使得新建模方法的引入成为可能，为计量经济学建模方法发展提供了空间。

3.估计方法和检验方法更加多样化。非均值模型一方面沿用了均值模型中的ML等估计方法，另一方面发展出了GMM、LAD、IFM及伪ML等方法；针对非均值模型的特点，模型检验拓展到拟LR检验、BDS检验、Wald检验、K-S检验等。这些估计与检验方法成为计量经济建模方法的重要组成部分，充实壮大了现代计量经济学的建模方法论体系。

4. 非均值模型适用领域广泛，拓展了计量经济学的应用范围。非均值模型弥补了传统的均值模型解决不了的问题，比如方差模型研究与波动性相关的领域；分布函数模型对尾部相关性研究尤为有效；持续时间模型研究事件的持续期间的长度等；分位数模型解决了随机项出现异方差或不服从正态分布问题，等等，从而推动了计量经济学方法在经济学实证研究和解决现实经济问题中的应用。

5. 从不同层面发展了计量经济学学科体系。计量经济学是一个开放的学科体系，非均值模型建模方法大大完善了计量经济学学科体系，出现了一些新的计量经济学学科分支，例如，在分位数模型和离散选择模型基础上，发展了微观计量经济学，在方差模型基础上发展了金融计量学，等等。

参考文献：

[1]李子奈，叶阿忠.高级计量经济学[M].北京：清华大学出版社，2000.

[2]高铁梅.计量经济分析方法与建模(第二版)[M]. 北京：清华大学出版社，2009.

[3]金玉国.非经典计量经济建模方法论的特征分析与比较研究[J].统计研究，2011，(01)：92-98

[4]金玉国. 计量经济学中的潜变量模型:一个方法论角度的考察 [J].统计研究，2012，(09)：46-52.

[5]武东.ARCH类模型在应用中的比较分析[D].上海师范大学，2004.

[6]覃龙.连接函数(Copula)及应用[D].新疆大学，2007.

[7]McFadden, D. Economic Choices[M], New York: American Economic Reviews, 2001: 351-378.

[8]Lane W. R, Looney S .W & Wansley J .W. An application of the Cox Proportional Hazards Model to bank failure[J].Journal of Banking and Finance, 1986.

[9]Barnes M. & W. Hughes, A quantile regression analysis of the cross section of stock market returns[J].Working Paper, 2002.