城市轨道交通动态杂散电流理论分析及计算
2014-06-21陈志光秦朝葵唐继旭
陈志光 秦朝葵 唐继旭
(同济大学机械与能源工程学院,201804,上海∥第一作者,博士后)
0 引言
城市轨道交通列车运行会产生杂散电流,对埋地燃气管道及钢轨、盾构等产生腐蚀。国内外都有大量这方面的报道[1-3]。随着我国城市轨道交通及燃气管网的迅猛发展,这一问题将更加突出。城市轨道交通杂散电流的大小与列车的运行有直接关系,同时也受轨道与大地过渡电阻、管道防腐层电阻、土壤电阻率等众多因素影响。影响因素的多样性及源头的动态性,为城市轨道交通杂散电流检测判定及分析带来很大困难。为此,建立轨道交通杂散电流泄漏模型,对其变化规律进行分析,为现场测试和工程防护提供理论依据,具有一定的现实意义。
从严格意义上讲,杂散电流分布的数学模型很难推导。在一定简化的基础上,国内已有研究建立了轨道-大地结构、轨道-排流网-大地结构、轨道-排流网-埋地金属-大地结构等城市轨道交通杂散电流泄漏模型,对相关参数变化时杂散电流变化情况进行了分析[4-8]。但现有模型考虑的均是轨道交通侧杂散电流的源头泄漏情况,对杂散电流在土壤中的分布、不同管道防腐状态,以及管道距轨道不同距离时埋地管道中杂散电流的变化没有考虑。并且,当前模型均回避了土壤电阻的计算,或忽略或将大地电阻折合到过渡电阻中。这一假定大大简化了公式及计算,但无法分析杂散电流在土壤与埋地管道中的分布。此外,计算中只分析了轨地过渡电阻、土壤电阻、管道防护电阻等均匀分布情况,而实际上局部破损情况下杂散电流的分布研究则更具有实际意义。
本文在轨道结构模型分析的基础上,对轨道与埋地管道之间土壤电阻进行了计算,建立双边供电模式下轨道-排流网-大地-埋地金属多层电阻模型;分析了管道防护层、管道与轨道距离、土壤电阻率等参数的影响,并对过渡电阻存在局部破损点状态下的杂散电流分布情况进行了计算。
1 城市轨道交通杂散电流理论模型
1.1 模型建立
我国现有城市轨道交通线路以地铁为主。上海市地铁列车一般均采用DC 1 500V架空接触网双边供电,走行轨回流。为减少杂散电流泄漏,采取了设置垫片、绝缘橡胶等措施以增大轨地过渡电阻;同时在轨道下方混凝土内设置排流网,进行杂散电流收集回流。轨道交通杂散电流的流经路径是在列车动车车轮处由轨道向外泄漏,经轨道道床结构、排流网进入土壤,由土壤流回变电站;或经土壤进入管道,由管道流至变电站附近,再经土壤、轨道道床结构等回到变电站。按照杂散电流泄漏路径,针对管道与轨道平行分布时的情况,将轨道、排流网、大地、埋地燃气管道等简化为层叠的电阻,不同层之间以过渡电阻连接。杂散电流流通路径可看作轨道-排流网-大地-埋地管道相互并联的电流回路。所建立的四层电阻网络模型分布如图1所示。

图1 轨道-排流网-大地-埋地管道电阻分布图
为方便计算,进行如下假设:①城市轨道交通列车运行采用双边供电模式,选取某一供电分区进行计算;②列车的回流电流与距两个供电所之间的距离成正比,且所有电流最终回流至两个供电所;③两供电所之间仅有一列列车运行,列车取流电流在运行期间保持不变。列车双边总供电电流为I,I1、I2为两侧回流电流。对各节点列基尔霍夫电流定律方程可得:

式中:
Rg——轨道纵向电阻;
Rt——轨道对排流网过渡电阻;
Rp——排流网纵向电阻;
RT——排流网对地过渡电阻;
Rd——大地纵向电阻;
R1——埋地管道对地过渡电阻;
Rr——管道纵向电阻。
1.2 土壤电阻计算
土壤电阻是影响杂散电流在大地与管道之间分配的重要因素。土壤电阻受土壤电阻率、所考虑土壤电阻区域长度、相应区域面积等参数影响。现对管道与轨道平行时的管轨之间土壤电阻进行计算。平行管道方向的土壤电阻定义为土壤纵向电阻,垂直管道方向的土壤电阻定义为土壤过渡电阻。排流网均匀布置在轨道下部,各钢筋之间具有良好的电连续性。
1.2.1 土壤纵向电阻计算
假定城市轨道交通泄漏电流呈均匀分布,将管道与轨道之间的环形土壤面积作为泄漏杂散电流在土壤中的回路,平行于管道方向的土壤纵向电阻截面积S计算如式(2),长度为l的土壤纵向电阻R如式(3)。

式中:
L——埋地燃气管道与地铁隧道外壁距离;
ρa——土壤地阻率;
l——计算土壤纵向电阻的土体长度。
1.2.2 土壤过渡电阻计算
埋地轨道与管道之间土壤横向电阻可看作相并联的过渡电阻。管道位于地铁隧道一侧,且地铁隧道直径D远大于管道直径d。在一定的纵向长度Δx方向上,土壤过渡电阻计算截面F取值见图2所示,即土壤过渡电阻Ra计算如下式:
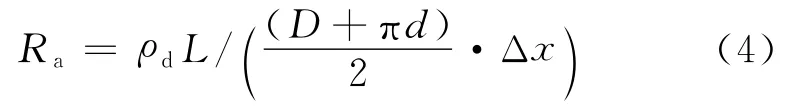
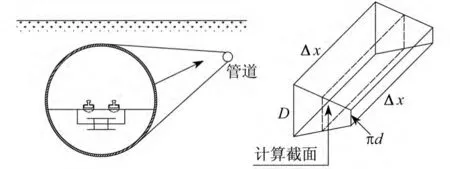
图2 土壤过渡电阻计算截面积示意图
2 模拟计算
2.1 计算参数选取
利用Matlab软件编程对城市轨道交通杂散电流在土壤中分布及对燃气管道影响进行计算,分析在供电区间、轨道电阻、轨地过渡电阻确定的情况下,管道与地铁隧道的距离、管道防腐层、土壤电阻率变化对管道杂散电流的影响,以及轨地过渡电阻、管道防腐层存在局部破损时,杂散电流在土壤及管道中的分布。计算中列车位于两变电站中间,各基本计算参数如表1所示[9-10]。

表1 模拟计算的基本参数
2.2 过渡电阻均匀分布状态计算
2.2.1 管道与地铁隧道的距离对杂散电流分布影响
分析管道与地铁隧道不同距离时杂散电流分布,分别取L=1m、L=10m、L=100m,其余参数选取基本参数。大地电流、泄漏入管道电流、管道电流的变化如图3。
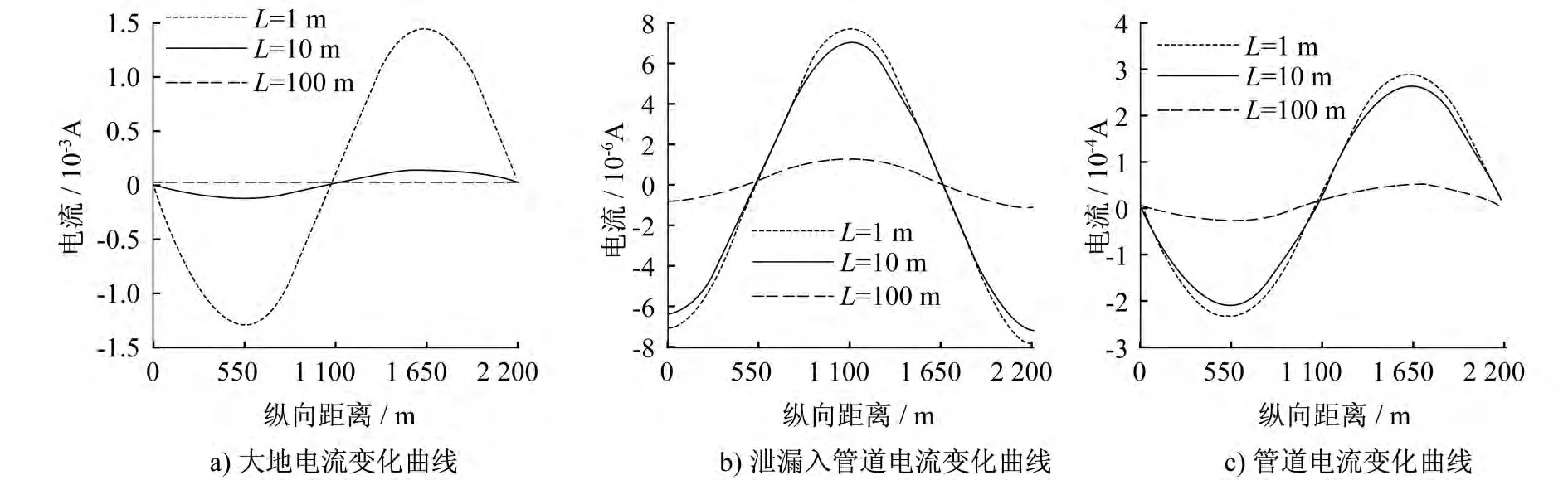
图3 不同的管道与地铁隧道间距下的电流变化曲线
随管道与地铁隧道间距的增大,杂散电流回路中土壤纵向电阻减小,管轨间土壤过渡电阻增大。由图3可得,土壤回路分流增大,土壤泄漏入管道电流减小,管道中电流减小。管道与地铁隧道距离的增大可有效减小管道中杂散电流。计算中轨地过渡电阻、土壤防腐层电阻满足设计要求,且各电阻均匀分布,此时各电流均很小,泄漏入管道的电流在几个微安量级,对管道影响很小。
方案实施过程中,通过及时跟踪分析动态资料,对原有方案进行适当调整和完善,使其最优化。在此基础上,按照探明或控制储量的规范对储量上报方案进行研究和优选,确定储量参数,最终完成储量的上报工作,并对整个精细勘探研究过程进行总结,指导下一步的勘探和开发。
2.2.2 不同管道防腐层对杂散电流分布的影响
管道防腐层电阻Rf取值为100Ωm2、1 000 Ωm2、5 000Ωm2、10 000Ωm2时,分别对应于管道防腐层防护级别为“劣”、“差”、“良”、“优”[11],其余参数皆取基本参数。大地电流、泄漏入管道电流、管道电流的变化曲线如图4。
由图4可得,随着管道防护层绝缘电阻的增大,土壤电流增大,土壤泄漏入管道的杂散电流减小,管道中电流减小。当管道防护层达到防腐级别“良”时(Rf=5 000Ωm2),土壤泄漏入管道电流值变化较小(处于微安级),与Rf=10 000Ωm2即防腐级别“优”相比差别不大;各点电阻均匀分布时,满足标准的防腐层可有效减小管道中的杂散电流。
2.2.3 土壤电阻率对杂散电流分布的影响
土壤电阻率ρd受土质、含水率、季节气候等条件影响很大。常见土壤腐蚀性分级标准规定:ρd<20Ωm为强腐蚀性土壤,ρd=20~50Ωm为中腐蚀性土壤,ρd>50Ωm为弱腐蚀性土壤。分析ρd对杂散电流分布的影响时,ρd取5Ωm、50Ωm、100Ωm,分别对应强、中、弱腐蚀性土壤环境,其余参数皆取基准参数。大地电流、泄漏入管道电流、管道电流的变化曲线如图5。

图4 不同防腐层情况下的电流变化曲线
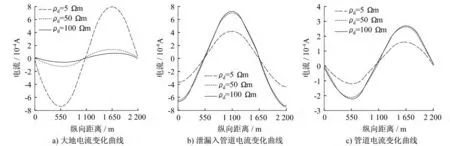
图5 土壤电阻率对各电流的影响
由图5可得:随土壤电阻率的增大,大地电流减小,管道电流、土壤泄漏入管道电流略微增大;随土壤电阻率的增大,土壤电阻增大,杂散电流泄漏减小,已泄漏的杂散电流经管道回流部分增大,但与防腐层级别、管道距地铁隧道距离相比,土壤电阻率变化对管道电流与土壤电流分配的影响较小。
2.3 局部破损点杂散电流变化
轨地过渡电阻及管道防腐层总会存在局部破损,造成杂散电流漏点。因此,存在局部破损时的土壤杂散电流分布计算更具有现实意义。假定各参数值整体上保持一致,在某具体点人为模拟局部破损。现分别对无破损点、1个破损点、2个破损点三种情况进行了计算,并对存在2个破损点时不同管道与地铁隧道距离、不同管道防腐层级别的杂散电流分布进行分析。
2.3.1 不同破损点计算对比
列车位于两供电所中间位置,破损点位置及破损处电阻值见表2所示,其余参数选取基本参数。分别对无破损点、1个破损点、2个破损点三种情况进行了计算。其大地电流、泄漏入管道电流、管道电流的变化曲线如图6。
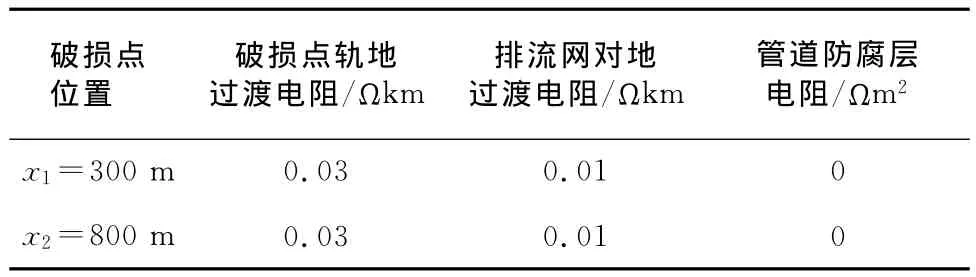
表2 破损点位置及相应过渡电阻值

图6 不同数量破损点下各电流分布曲线
由图6可得:过渡电阻及管道防腐层存在破损点时,破损点处电流发生突变,与无破损时相比增大数十倍,且经破损点流入的电流导致管道其余部位电流泄漏增大,泄漏电流大于无破损点情况,增加了腐蚀风险;2个破损点存在时,在管道防腐破损点之间形成电流流入、流出回路,管道破损点处泄漏电流大于1个破损点情况。
当有2个破损点时,破损点2(x2=800m)泄漏电流方向为正,杂散电流流入管道;破损点1(x1=300m)泄漏电流方向为负,杂散电流从管道流出。列车位于两变电站中间位置时,破损点2距列车较近,破损点1邻近供电所,杂散电流方向与列车位置有关。
2.3.2 存在局部破损时管道与地铁隧道间距的影响
现对2个破损点情况下管道与地铁隧道间距的影响进行分析。破损点位置及参数与表2相同。管道与地铁隧道间的距离L分别取为1m、10m、100 m,其余参数选取基本参数。大地电流、泄漏入管道电流、管道电流的变化曲线如图7。
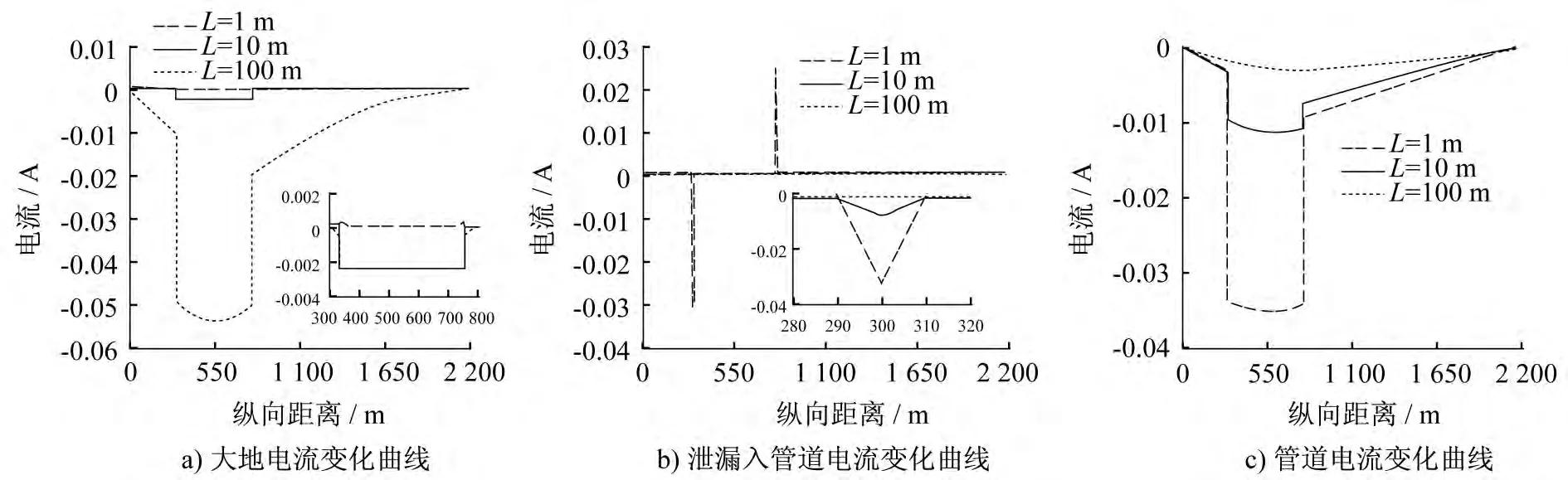
图7 2个破损点情况下管道与地铁隧道间距对电流分布的影响
由图7可得:随着管道与地铁隧道距离的增加,大地电流增大,管道电流、泄漏入管道电流急剧减小,电流突变趋于平缓,经大地泄漏至管道的杂散电流及管道电流迅速减小。距离增大能明显减少泄漏杂散电流对管道的影响。
2.3.3 存在局部破损时管道防腐层的影响
现对2个破损点情况下的管道防腐层影响进行计算。破损点位置及参数与表2相同,管道防腐层电阻Rf分别取100Ωm2、1 000Ωm2、5 000Ωm2、10 000Ωm2,其余参数选取基本参数。大地电流、泄漏入管道电流、管道电流的变化曲线如图8。
由图8可得,随着整体防腐层保护程度的提高,各破损点电流突变趋于平缓,大地电流和管道电流均减小。就泄漏入管道电流而言,流入流出管道表面整体电流随着防腐层保护程度的提高而减小,但破损点处电流随管道其余部位防护程度的提高而增大。对杂散电流干扰区域,当存在局部破损点时,随管道整体防腐程度的提高加速了破损点的腐蚀。
图8 2个破损点情况下不同防腐层对电流分布的影响
3 结论
城市轨道交通杂散电流会对埋地燃气管道产生严重腐蚀,对其变化规律及分布进行理论分析,为试验及防护措施提供理论依据,具有一定的现实意义。
本文对地铁隧道与埋地管道之间的土壤电阻进行了计算,建立了双边供电模式下轨道-排流网-大地-埋地金属多层电阻模型,分析了管道防腐层、管道与地铁隧道距离、土壤电阻率等参数对杂散电流分布的影响,并对过渡电阻局部破损状态下的杂散电流进行了计算。
计算结果表明:过渡电阻及管道防腐层存在局部破损时杂散电流的影响远远大于不破损时电阻均匀分布的情况;管道与地铁隧道间的距离及管道防腐电阻的增大能有效减小管道杂散电流,土壤电阻率变化对管道电流与土壤电流分配的影响较小;当存在局部破损时,破损点处电流泄漏随管道其余部位防护程度的提高而迅速增大,故应加强对杂散电流存在区的管道防腐层施工管理。
[1]Fitzgerald Iii J H,Lauber M D.Stray current control for the St.Louis metrolink rail system[J].Materials Performance,1995,34(1):21.
[2]Pignatelli Jr P.Stray current corrosion on underground utilities:a case history[J].Materials Performance,1985,24(2):30.
[3]林江,唐华,于海学.地铁迷流腐蚀及其防护技术[J].建筑材料学报,2002,5(1):72.
[4]徐光强.直流牵引供电系统中杂散电流防护方案研究与设计[D].成都:西南交通大学,2003.
[5]王崇林,马草原,王智,等.地铁直流牵引供电系统杂散电流分析[J].城市轨道交通研究,2007(3):52.
[6]庞原冰,李群湛.地铁杂散电流模型讨论[J].重庆工学院学报:自然科学版,2007,21(11):110.
[7]陈志光,秦朝葵,张杨竣.轨道交通杂散电流腐蚀研究现状[J].世界科技研究与发展,2010,32(4),497.
[8]李威.地铁杂散电流腐蚀监测及防护技术[M].徐州:中国矿业大学出版社,2004.
[9]东留宝,于宏,冯宝鹤.浦东地区土壤电阻率调查[J].上海煤气,1994(5):44.
[10]CJJ 49—92地铁杂散电流腐蚀防护技术规程[S].
[11]SY/T 5918—2004埋地钢制管道外防腐层修复技术规范[S].
[12]黄玉苹.城市轨道交通杂散电流防护系统[J].城市轨道交通研究,2012(12):117.
