基于NX8.5的打纬摇轴载荷及模态分析
2014-06-21杨剑宇
杨剑宇
打纬机构是织机的五大机构之一,它将纬纱打入织口,使经纬纱交织,形成符合设计要求的织物。目前,织机的打纬机构主要分为共轭凸轮式和连杆式两类。由于共轭凸轮式打纬具有动程小、运行平稳等优点,故高速的剑杆织机常采用共轭凸轮式打纬机构。而打纬摇轴是共轭凸轮式打纬机构的重要零件之一,其在打纬过程中,需要承受来自凸轮和滚子的较大载荷。另外,打纬摇轴伴随着旋转,自身和其他外界因素激励而发生共振,易造成打纬机构的机件损坏。同时,随着现代织机向高速、高效、高品质和高适应性方向的发展,对织机的打纬机构主要部件提出了更高的要求。因此,需要更正确地计算摇轴在载荷下的应力、应变和固有频率等参数,以提高零件在工作时的安全性。
UGNX是一款集CAD/CAM/CAE于一身的企业级的软件。其中,它的有限元分析,也就是高级仿真模块,在长时间的发展中吸纳了很多世界优秀的有限元软件,如 MSC.Nastran、I-deals、Adina和 LSDYNA等众多的功能和优点,特别是它的结构分析功能具有计算精度高、运行速度快、操作界面友好的优势,得到了国防、航空航天、车辆、船舶、机械和电子等众多行业的接受和认可,其分析结果已成为航天等级工业CAE标准,获得美国联邦航空管理局(FAA)认可。它的高级仿真模块包含NX前、后处理和NXNastran求解3个基本的组成部分,并具备了在众多领域中解决工程问题的解算类型。本文通过NX8.5软件完成了打纬摇轴的建模,并对其进行模态及在载荷下应力应变的分析,为合理设计打纬摇轴提供理论依据。
1 打纬摇轴模型的建立
织机的打纬机构目前主要分为共轭凸轮式和连杆式2类,其中具有小动程、运行平稳等优点的共轭凸轮式常用于剑杆织机。共轭凸轮式打纬机构示意图如图1所示。
打纬摇轴是共轭凸轮式打纬机构的重要零件。本文利用NX软件对打纬摇轴进行了模型的建立。建立的模型如图2所示。
2 打纬摇轴载荷条件下的分析

图1 打纬机构示意图
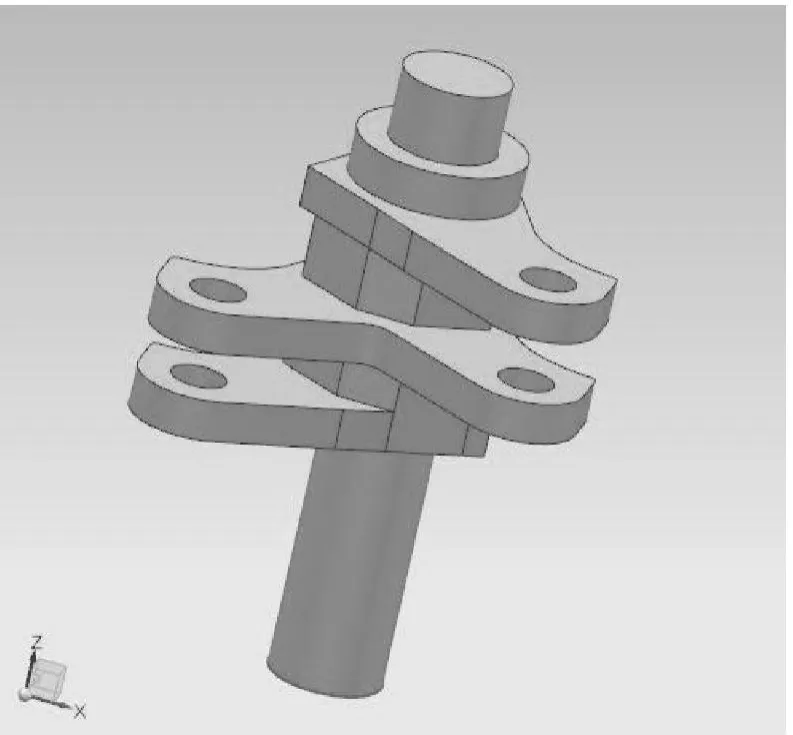
图2 NX软件建立的打纬摇轴模型

图3 打纬摇轴的单元网格划分
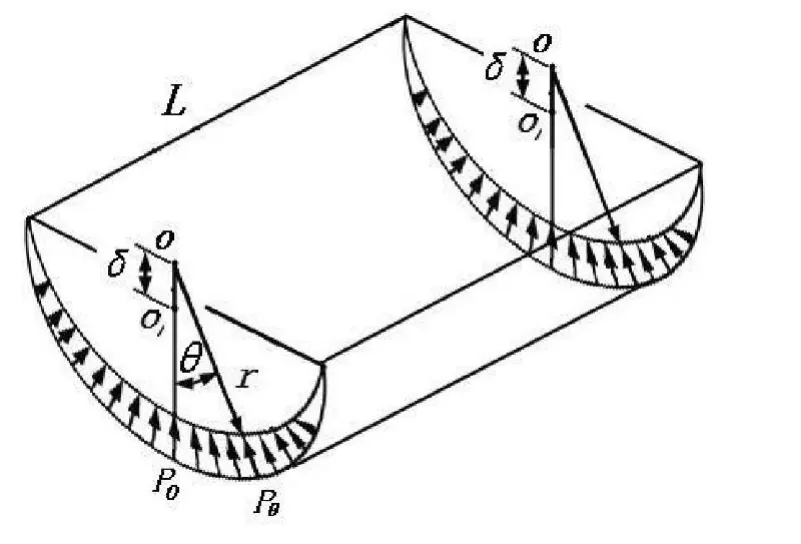
图4 载荷分布示意图
2.1 单元划分
单元网格的划分是有限元分析前处理工作之一,也是有限元分析计算的基础。网格质量的优劣是决定计算精度的重要环节,特别是对于大型和复杂模型来说,网格划分相当耗时,所以一味的减少单元大小对提供计算精度没有益处。根据模型和单元类型的特点,本文中打纬摇轴采用CTETRA(10)四面体10节点进行划分,单元大小采用10mm。单元划分后的模型如图3所示。
2.2 定义材料属性
不同的分析和解算类型需要定义不同的材料参数,其中质量密度、杨氏模量和泊松比是弹性范围内静力学分析最基本的3个参数。本文中打纬摇轴的材料采用40CrNiMoA。其中质量密度 约为7830kg/m3,杨氏模量约为209GPa,泊松比约为0.3,抗拉强度b≥980 MPa,屈服强度s≥835 MPa。
2.3 载荷的施加及模型的约束
在施加外部载荷的作用下,会使打纬摇轴产生应力和应变,而约束条件不同也会对最终的计算结果起到很大的作用影响。
打纬摇轴的滚轮轴孔上的径向压力不是均匀的,它的受力方式如图4所示。图中为轴孔的轴向长度。
本文中假设打纬摇轴的滚轮轴孔在受到载荷后仍保持或近似保持圆形,在最大受力P0处的径向变形为 ,则圆心角为 处的轴孔径向形变量为 ()=cos滚轮轴孔上受到的压力方向均沿径向方向垂直于轴孔表面。设滚轮轴孔的材料应变系数为 k,则最大压力P0处为:

进而得出在任意的圆心角 处轴孔表面受到的压力为
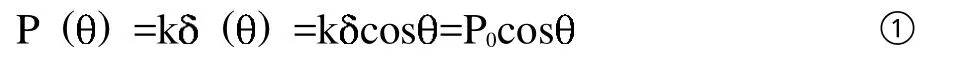
同时,打纬摇轴的滚轮轴孔受到的力是沿孔径向120°范围内,按照余弦方式施加到轴孔上的,那么将每个点上的力按x轴和y轴方向分解后分别为:
最后,其应用场景满足5000万像素以上的全画幅数码相机,同时可以满足当前8K视频技术的高分辨率要求,是一支着眼于未来的高品质镜头。

式中,r为孔的半径, 为圆心角,P为120°弧段中点处的表面力的集度。
根据式①、②和③,得出轴孔在x轴和y轴的载荷 、 :
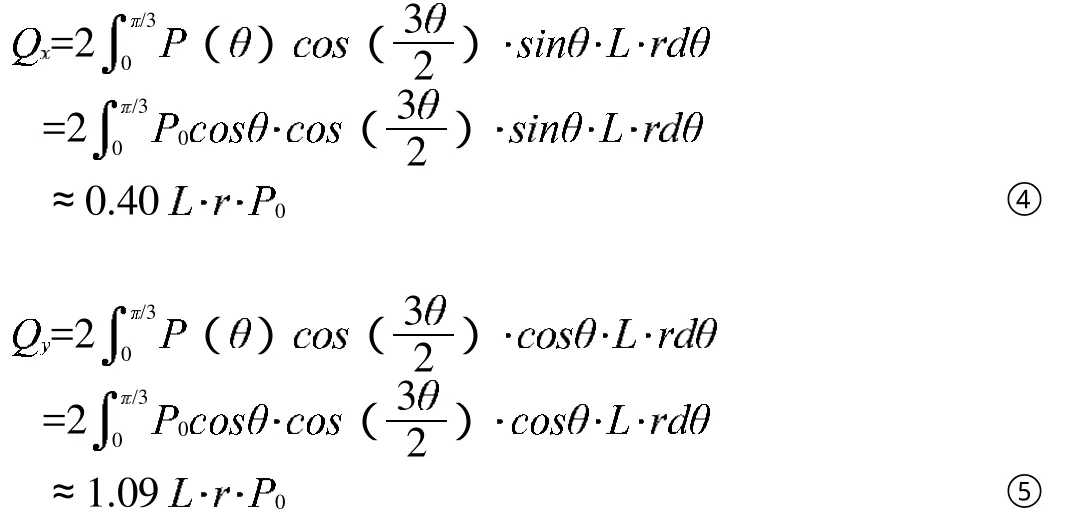
按照式④和⑤可以算出打纬摇轴的滚轮轴孔上x轴和y轴的载荷,并在NX高级仿真模块中将所计算的载荷施加在轴孔表面上。
配合ADAMAS软件计算得出:
打纬载荷在主动轮滚轮轴孔处为 =4743.7 =12807.9
从动轮轮滚轮轴孔处为 =5467.9 =-14763.5
另外,在施加载荷的同时,也需要对模型进行约束。打纬摇轴受力的最大值是在打纬时的瞬间静止状态,因此将两端圆柱面施加固定约束,即DOF1、DOF2、 DOF3、 DOF4、DOF5和DOF6均设置为固定,用以模拟打纬摇轴在受力最大时瞬间静止的状态。
2.4 解算器的选择
NX高级仿真支持的线性静力学分析的解算器主要有NX Nastran-SESTATICS 101,单个约束:该解算类型可以创建具有唯一载荷的子工况,但是每个子工况均使用相同的约束条件;NXNastran-SESTATICS 101,多个约束:该解算类型可以创建多个子工况,每个子工况既包含唯一的载荷又包含唯一的约束,设置不同子工况参数并提交结算作业时,解算器将在一次运行中求解每个子工况。
本文对打纬摇轴采用了分析类型为结构,解算类型为Nastran-SESTATICS101,单个约束的解算方案。
2.5 解算结果及分析
通过NX高级仿真模块的分析计算,得出图5的应变云图和图6的应力云图。
由图5的 Von-Mises应变云图中可以得出,打纬摇轴发生应变的最大值是在滚轮支架的顶端,位于208014单元,应变的最大值为9.255×10-4mm,另一侧位于209530单元的滚轮支架应变值为8.327×10-4mm。
由图6的冯氏应力云图中可以看出,应力主要分布在轴体与相邻台阶面的连接处,轴体与滚轮支架形成的相贯线处,滚轮轴孔的半圆面等易于发生应力集中的区域。其中,应力最大的是轴体与相邻台阶面的连接处,应力值为206MPa,位于107135单元。表1给出了本次分析的主要结果。
由表1的数据可以看出,打纬摇轴的最大应力206MPa相对于材料的屈服强度835 MPa还是有很大的安全余地的,另外,打纬摇轴的最大应变9.255×10-4mm能够满足打纬摇轴在打纬过程中的工艺指标,所以在本文所述的工作条件下,打纬摇轴能够满足生产过程中的使用要求。

图5 打纬摇轴应变云图
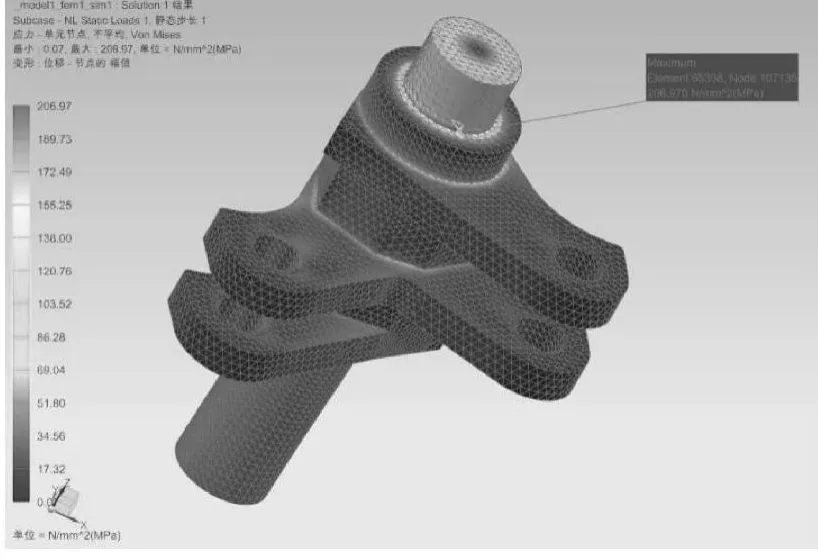
图6 打纬摇轴冯氏应力云图

表1 载荷分析结果
3 打纬摇轴模态分析
模态分析是任何涉及非静力结构设计的一个很重要的部分,用来确保产品和关键零部件的固有频率不会与输入频率或者外界强迫作用的频率一致,这些外界强迫作用是十分常见的。模态分析实质就是将一个弹性连续体的振动问题,离散为一个或者有限个节点位移为广义坐标的多自由度系统的振动问题,其运动微分方程可以表示为:
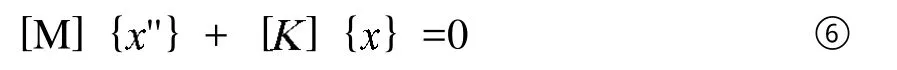
式中,[M]表示构件的总体质量矩阵;[]表示构件的总体刚度矩阵;{}表示节点位移列阵;{''}表示节点位移对时间的二阶导数。
上式的解可以假设为如下形式:

式中,{ }为 阶向量; 是向量 的振动频率; 是时间变量; 是由初始条件确定的时间常数。将式⑦带入⑥得到如下特征方程:

求解上述方程可以确定 和 ,可以得到 个特征值:
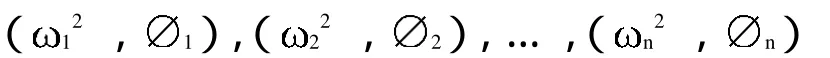
其中,特征值1,2,…,n代表构件的 个固有频率,或称为特征频率,并且满足:

特征向量1,2,…,n代表构件的 个固有振型,对应的幅值可以按照以下确定:
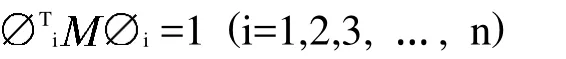
打纬摇轴在打纬过程中会承受周期性载荷的作用,可能会与旋转的主轴发生强烈的共振,致使动应力急剧的增加,导致打纬摇轴由于扭转疲劳和弯曲疲劳,在到达其设计寿命之前就被破坏。通常的静力学计算不能够完成相关的动力学分析,因此需要对打纬摇轴进行模态分析,从而确定打纬摇轴的固有频率和振型。
打纬摇轴的固有频率和振型是设计中的重要参数。通常主轴转速为400r/min,打纬摇轴转速略低于主轴转速,由推算出主轴频率f=6.667Hz。利用NX Nastran模态分析模块,计算出打纬摇轴的固有频率。计算时不考虑阻尼,也与外载荷无关。本文在进行模态计算时,使用了SOL103结算方案。网格划分与载荷分析相同。
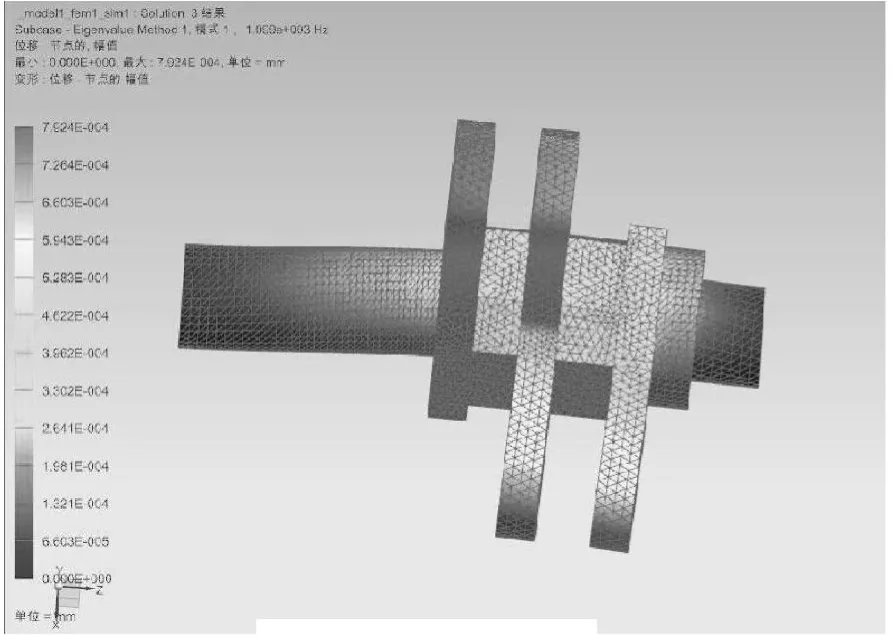
图7 1阶振型
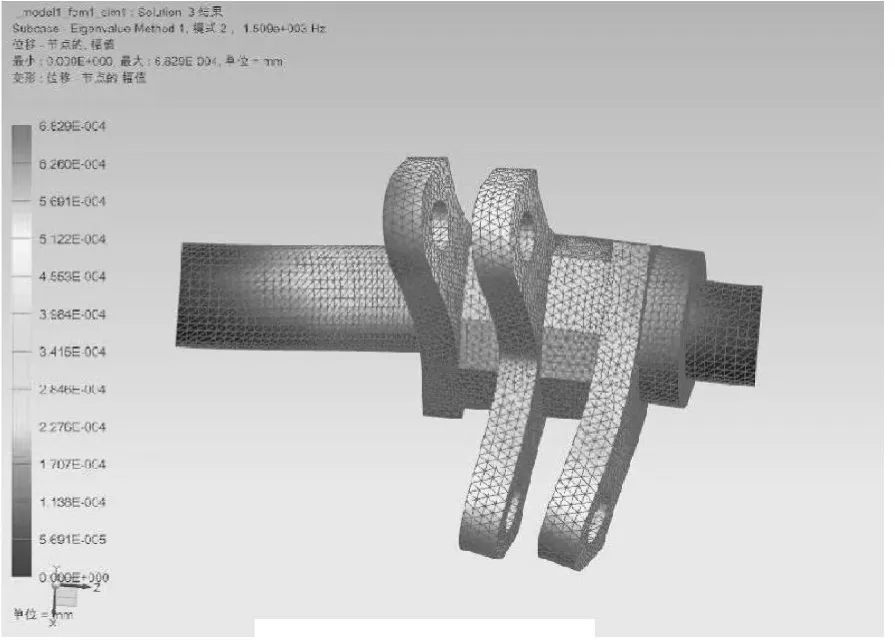
图8 2阶振型

图9 3阶振型
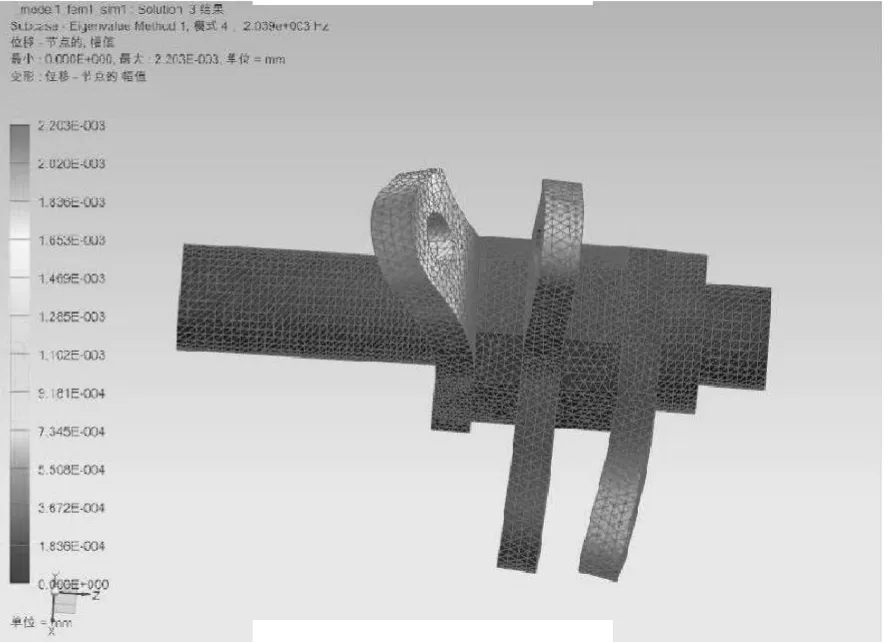
图10 4阶振型

图11 5阶振型

图12 6阶振型
本文取前10阶固有频率和振型,图7至图16为打纬摇轴的前10阶振型图。

图14 8阶振型

图15 9阶振型

图16 10阶振型
表2为打纬摇轴固有振动频率和振型分析结果。

表2 打纬摇轴模态计算结果
由模态计算结果可知打纬摇轴自身转动频率及主轴转动频率远小于第1阶的固有频率,因此,该打纬摇轴发生共振的可能性很小。
4 打纬摇轴改进措施
通过NX软件对打纬摇轴进行的载荷计算及模态计算,可以看出疲劳失效是打纬摇轴的主要失效形式。所以需要通过改进设计方案、加工工艺和装配方法来提高打纬摇轴的使用寿命。可以采取在容易产生应力集中的区域,如轴体与相邻台阶面的连接处,轴体与滚轮支架形成的相贯线等处进行倒圆角处理;取消原摇轴上的两组螺孔,改为铣一个平面;除了原先的拉线式组合装配方法,增加轴承座定位工装;采用带有倒角的加工刀具来处理加工面与毛坯面等措施,使打纬摇轴提高使用寿命,并减少在使用过程中因疲劳而造成的失效。
5 结语
本文通过UGNX8.5软件进行了打纬摇轴的建模,并对其进行了载荷及模态的分析。通过对打纬摇轴的静应力分析,可知轴体与相邻台阶面的连接处,轴体与滚轮支架形成的相贯线等处应力比较集中,通过将最大应力与屈服应力进行比较,得知该打纬摇轴的强度能够满足生产要求。通过模态分析,得出了打纬摇轴各阶的固有频率和振型,可知该打纬摇轴发生共振的可能性很小。通过对打纬摇轴计算结果的分析,提出了打纬摇轴设计的改进措施,为提高打纬过程的质量,提升剑杆织机的品质提供了一种较为可行的思路。
[1]沈春根,王贵成,王树林.UG NX 7.0有限元分析入门与实例精讲[M].北京:机械工业出版社,2010.
[2]滕兵.高性能剑杆织机打纬和引纬机构的设计与研究[D].上海:东华大学,2006.
[3]陈元甫,洪海沧.剑杆织机原理与使用(第二版)[M].北京:中国纺织出版社,1985.
[4]夏金国.织造机械[M].北京:中国纺织出版社,2001.
