基于无源性的鼠笼式感应电机转速控制系统
2014-06-20廖冬初秦庆江
陈 力,廖冬初,秦庆江,王 振
(湖北工业大学 电气与电子工程学院,湖北 武汉430068)
1 引言
自1982年Faraday发明首台直流电机以来,电机就广泛应用于现在工业的生产建设中,在工业生产所用电机中,感应电机占据了相当大的比例,其中又以鼠笼式感应电机为主。国内外学者对感应电机变频调速系统做了大量的研究,在调速范围、动态响应、输出性能等方面取得了突破性的进展。
感应电机是一个典型的非线性系统,变量间存在强耦合,转子变量测量困难,参数时变,要达到高精度控制比较困难。传统的矢量控制方法是对系统进行解耦控制,依赖于对系统非线性的精确抵消,在本质上是非鲁棒的。近年来,随着对非线性控制理论研究得不断深入,众多学者致力于对感应电机的非线性控制研究中,旨在进一步提高调速系统的动静态性能、抗干扰性、鲁棒性。
无源性控制(Passivity-based Control,简称PBC)是一种非线性反馈控制方法,在控制系统中采用无源性理论,是从能量及其转换的角度来分析的,是一种跟系统的输入和输出相关联的重要性质。简略地解释为:当一个系统的能量总是小于或者等于初始时刻的能量和外部提供的能量之和,即系统本身并不产生能量,只从外部吸收能量,则称这个系统是无源的。
本文在已有研究的基础上,将无源性理论在用到鼠笼式感应电机控制中,在无源性控制方法的基础上,借助于矢量控制的思想,将转子磁链给定值作为转矩控制器的一个输入,提出了一种满足系统无源性的状态变量取值方法,并在转矩控制器前面增加一个线性调节器,实现了对电机转速的控制。并在Matlab的Simulink中建立了系统模型,通过仿真证明,该方法能实现对鼠笼式感应电机的转速控制,系统稳定性好。
2 鼠笼式感应电机在两相旋转坐标系中的数学模型
在任意两相旋转坐标系中,鼠笼式感应电机的数学模型可用如下两个方程式来表示:

在式(1)中,Rs、Rr分别为定、转子各项绕组电阻;Ls、Lr分别为定、转子电感;Lm为互感;ω1为d、q坐标系旋转角速度;ωr为转子旋转电气角速度;ω2=ω1-ωr为转差角速度;ρ为微分算子d/dt;isd、isq分别为定子电流在d、q轴上的电流分量;ird、irq分别为转子电流在d、q轴上的电流分量;usd、usq分别为定子电压在d、q轴上的电压分量。
式(2)中,J为转子的转动惯量;f为阻尼系数;ωm为转子旋转机械角速度,ωr=npωm;ye、yL分别为电磁转矩和负载转矩;np为电机极对数。
3 鼠笼式感应电机的无源性
Romeo Ortega等人从机器人的无源性控制中受到启发,提出基于无源性的感应电机的控制方法。对感应电机的Eluer-Lagrange方程进行分析,将电机控制系统分成两个串联的无源子系统,即电气和机械两个子系统。又使得电气子系统严格无源,将第二个系统看成是对系统的无源性干扰,从而确保了系统的全局稳定性。
将鼠笼式感应电机任意两相旋转坐标系的状态方程(1)、(2)用Eluer-Lagrange方程表示如下:
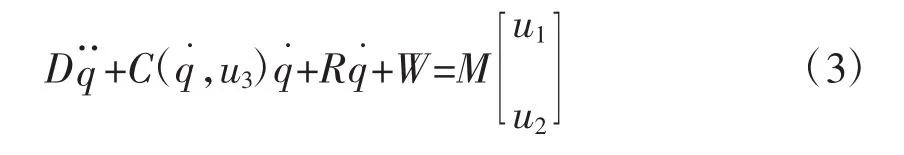
转矩方程为:

式(3)中的系数矩阵分别表示如下:


又已知C=-CT,故对方程(5)两边积分得:

在式(6)中,右侧是外部电源给感应电机系统的供给能量,左侧是感应电机系统的能力增量,根据无源性的定义,可知系统是严格无源的。
4 无源性控制器的设计
感应电机调速主要是通过转矩,在这里先设计转矩控制器,在设计过程中把转速做恒值处理。然后在转矩控制器的基础上设计转速控制器。
4.1 转矩控制器的设计

转子磁链幅值渐近跟踪:

在这里,定义系统的误差向量为e˙=q˙-q˙*,由鼠笼式感应电机的Eluer-Lagrange方程可得系统的误差方程如下所示:

对能量函数Hd求导可得
通过前面的分析可知,为了保证控制系统的稳定性,同时获得期望的跟踪性能,需要保证Ψ=0,可以通过选取适当的来实现。在本文中,借助于矢量控制中的转子磁链定向思想,当感应电机控制系统渐近地达到磁场定向时,转子磁链在d轴的磁链分量等于转子磁链幅值,d轴磁链分量等于0,即:

由方程(6)、(9)可得出:

由Ψ=0,转差速度ω2=ω1-npωm,以及方程(9)、(10)联立解得系统控制率如下所示:

在式(12)中,kp1、kp2是为了改善系统的动态响应及降低系统对参数变化的灵敏度而增加的阻尼项,这样就保证了整个鼠笼式感应电机控制系统的严格无源。其中:

4.2 转速控制器的设计
由上述可知,基于无源性控制的鼠笼式感应电机转矩控制器能有效地跟踪时变的转矩,因此要设计转速控制器,只需要建立一个转速误差反馈,利用比例积分调节器,即可得到理想的转速跟踪性能。通过一个转速闭环,再经过比例积分调节,就可以得到参考转矩如下式所示:

5 鼠笼式感应电机无源性控制Matlab仿真
借助于Matlab强大的仿真建模能力,利用Simulink中包含的功能原件,在上文的基础上建立了基于无源性控制的鼠笼式感应电机转速控制系统,基本思想是:以鼠笼式感应电机为控制目标,通过转速控制器得到期望转矩,然后通过转矩控制器得到SVPWM模块所需变量,并通过SVPWM为IGBT提供驱动脉冲来给感应电机供电。这其中又包括了转速测量模块、转子电流观测器模块等。系统控制框图如图1所示。

图1 基于无源性控制的鼠笼式感应电机转速控制系统框图
本系统中用于仿真的鼠笼式感应电机参数为:额定功率Pn=3kW;定子额定电压Un=380V,额定频率fm=50Hz; 额定转速n=1420r/min;定子电阻Rs=0.435Ω, 电感Ls=5mH; 转 子 等 效 电 阻Rr′=0.816Ω,等效电感Lr′=5mH;互感Lm=50mH;极对数=2;转动惯量J=0.19N·m2。
仿真过程如下:仿真算法采用adam算法,仿真时长1s,给定转速为1420r/min,空载启动,在0.6s时加负载55N.m。系统仿真结果如下:图2所示为转速波形图,图3所示为转矩波形图,图4所示为定子电流波形图。从仿真图可以看出,基于无源性的鼠笼式感应电机转速控制系统,能精确地跟踪转速,在0.3s达到给定转速和0.6s加负载时,电机电流、转矩都有相应的响应。

图2 基于无源性控制的鼠笼式感应电机转速波形图

图3 基于无源性控制的鼠笼式感应电机转矩波形图

图4 基于无源性控制的鼠笼式感应电机A相电流波形图
6 结论
无源性控制方法是一种非解耦的非线性反馈控制,是以系统的能量变化特性为基础,没有去抵消系统的非线性,因此对系统模型的依赖性小。以此为基础建立的控制器形式简单,能准确地跟踪转速的变化,动静态性能良好,鲁棒性好。
[1]Ortega R and Espinosa N.Torque and speed regulation of induction motors.Automatica,1993,29(3):621-633.
[2]Gokdere L U and Simaan M A.A passivity-based method for induction motor control.IEEE Trans.IE,1997,44(5).
[3]Romeo Ortega,Antonio Loria and Per Johan Nichlasson,et al.Passivity-based control of Euler-Lagrange System[M].New York:Springer,1998.
[4]Cecati C.and Rotondale N.Torque and speed regulation of induction motors using the passivity theory approach[J].IEEETrans.onIndustrialElectronics,1999,46(1):119-127.
[5]陈锋,徐文立.基于无源性的异步机自适应控制[J].自动化学报,2000,26(6):776-781.
