电动汽车电驱动系统的EIMC及其鲁棒性研究*
2014-06-20董凤莲屈稳太
董凤莲,屈稳太
(1.太原科技大学电子信息工程学院,山西太原030024;2.浙江大学宁波理工学院,浙江宁波315100)
1 引言
电机驱动系统是电动汽车的核心。与其他电机相比,永磁无刷直流电动机是一种高性能的电动机,它没有换向火花,没有无线电干扰,具有更高的能量密度和效率,在电动汽车中获得了最广泛的应用[1]。由于电动汽车运行的环境比较复杂,永磁材料在受到振动、高温和过载电流作用时,导磁性能可能会下降或发生退磁现象,将降低永磁电动机的性能,进而影响电动汽车的运行质量。针对这一问题,本文采用增强型内模控制方法,显著提高了电动汽车适应恶劣路面的行驶能力,使电动汽车稳定可靠、高性能地运行。
内模控制是通过被控对象与内部模型的输出误差来调整控制器的输出,使系统稳定在目标范围内[2],因此,内模控制可以消除不确定性的影响。由于内模控制具有结构简单、鲁棒性强、能消除不可测干扰等优点,近年来已在快响应的电机控制中受到了广泛的关注。为了充分发挥内模控制的优势,很多学者把内模控制与各种控制方法相结合形成综合控制策略。
J C Gonzalez-Gomez等人用基于内模的实时神经模糊控制方法来控制直流电机,可以减少因模型失配和外界干扰引起的误差[3]。针对双馈式感应发电机,N Amuthan等人设计了一种直接模型参考自适应内模控制器(DMR-AIMC)[4]。文献[5]将内模控制和自适应逆控制相结合,有效提高了电动液压振动台的跟踪精度。由于系统的控制性能与模型的精度密切相关,文献[6]根据非线性内模控制对高斯过程模型进行了扩展,提供了一个分析预测的方法。本文通过对内模控制结构进行改进,引入一种增强型内模控制(EIMC)方法,使系统的鲁棒性得到增强。针对电动汽车控制系统模型复杂多变的情况,将EIMC控制结构应用于电动汽车控制系统的速度控制中。在模型失配和负载扰动情况下,研究了调速系统的品质鲁棒性和鲁棒稳定性,并通过仿真实验与传统的PI调节器进行分析和对比。
2 系统建模
2.1 电动汽车动力学模型
根据理论力学和流体力学原理,可以分析电动汽车在行驶过程中的受力。电动汽车在行驶时,动力由电动机的驱动力、斜坡动力(下坡)提供,阻力主要由空气阻力、滚动阻力、斜坡阻力(上坡)、加速阻力组成[7]。
电动汽车动力学模型为:

式中:Fl为汽车所受的牵引力;Fw为空气阻力;Fr为滚动阻力;Fi为斜坡阻力;Fj为加速阻力。
(1)牵引力

式中:Te为电磁转矩;n1、n2分别为主减速器和变速箱的变速比;r为车轮半径。
(2)空气阻力
根据空气动力学原理,空气阻力可近似表示为:

式中:ρa为空气密度;ca为空气阻力系数;s为汽车迎风面积;v为汽车行驶速度。
(3)滚动阻力、斜坡阻力和加速阻力可分别表示为[8]:

式中:m为汽车质量;c1、c2为常数;g为重力加速度;χroad为路面坡度;v˙为汽车行驶加速度。
2.2 电动汽车电机数学模型
电机角速度为:

式中:ωm为电机的角速度。
将汽车的受力归算到汽车的驱动单元,即式(2)、(6)、(7)代入式(1),可得:

根据PMBLDCM方程

其中:Ce、Cm分别为电机反电动势系数和转矩系数,可建立电动汽车用PMBLDCM的数学模型。
3 增强型内模控制(EIMC)及其鲁棒性
3.1 增强型内模控制结构
实际的控制系统存在模型不确定性,为了进一步增强内模控制对模型失配和外界干扰的鲁棒性,需要对内模控制结构进行改进。将建模误差反馈到被控对象的输入端,强迫被控对象的输出跟随内部模型的输出[9]。增强型内模控制(EIMC)结构,如图1所示。

图1 EIMC结构图
3.2 EIMC系统的鲁棒稳定性
定理1:当模型失配时,基于EIMC的闭环系统稳定的充分必要条件为:

证明:用乘性不确定性界来描述模型的不确定性,闭环系统稳定的充分必要条件为:

内模控制器GI1(jω)和反馈控制器GI2(jω)设计为:

基于式(11)、(12)和(13),可以证明 式(10)成立。
3.3 EIMC系统的品质鲁棒性
定理2:当模型失配时,基于EIMC的闭环系统具有品质鲁棒性的充分必要条件为:

证明:闭环系统具有品质鲁棒性的充分必要条件为[10]:

通过式(13)、(15)和(16)可以得到式(14)。式中,w为灵敏度函数的加权因子,一般情况下取w=0.3-0.9[2]。根据式(14),可以看出通过调整滤波器的滤波时间可以使系统获得较好的品质鲁棒性。
4 电动汽车驱动系统控制器及其鲁棒性
4.1 闭环调速系统的控制器设计
将EIMC引入电动汽车的PMBLDCM调速系统中,根据增强型内模控制原理设计调速系统的速度控制器。同时,电流控制器采用传统的PI调节器。电流环的动态结构图,如图2所示。

图2 电流环动态结构图
设计电流控制器为:

选择τi=L/R,将电流环等效为速度环中的一个环节,则电流环等效为:

忽略高次项,将闭环传递函数近似等效为:

速度环的动态结构图,如图3所示。

图3 转速环动态结构图
根据增强型内模控制原理设计速度控制器,采用EIMC的转速环动态结构图,如图4所示。

图4 采用EIMC的转速环动态结构图
为了增强系统的鲁棒性,引入低通滤波器Gf(s),将控制器GACR(s)和GI2(s)设计为:

选取1型低通滤波器:

在模型结构参数已知的条件下,电流控制器设计好后,速度控制器只有一个可调参数λn,克服了参数整定复杂的缺点。
4.2 闭环调速系统的鲁棒性
闭环调速系统存在模型不确定性时,系统的鲁棒性由鲁棒稳定性和品质鲁棒性组成。
当模型失配时,通过式(11)、(22)可知,采用EIMC的闭环调速系统稳定的充分必要条件为:

上式表明:当K一定时,通过调整λn可以保证闭环调速系统稳定。
当模型失配时,根据式(14)、(21),采用EIMC的闭环调速系统具有品质鲁棒性的充分必要条件为:

由上式可以看出:当K一定时,调整λn可以使调速系统获得较好的品质鲁棒性。
5 系统仿真
本文采用永磁无刷直流电机作为仿真实验对象,分别采用EIMC方法和传统PI调节,比较速度控制鲁棒性的强弱。永磁无刷直流电机(PMBLDCM)参数选取为:220V;l86A;300r/min。电动汽车传动系统参数选取为[8]:车体总质量m=1350kg;总惯量J=145kgm2;车轮半径r=0.29m;总变速比n=n1n2=7;迎风面积s=2.31m2;空气阻力系数ca= 0.32;空气密度ρa=1.205kg/m3;滚动阻力系数c1=8.8×10-2;c2=-6.42×10-4;g =9.8N/kg。
两种控制方法的仿真结果,如图5-图7所示。图5、图6和图7分别为路面凹凸不平、反电动势和转矩系数存在扰动和温度升高时电机速度与电流的变化过程,其中,(a)和(b)分别为速度的过渡过程和跟踪误差,(c)和(d)分别为直流电流的过渡过程和跟踪误差。

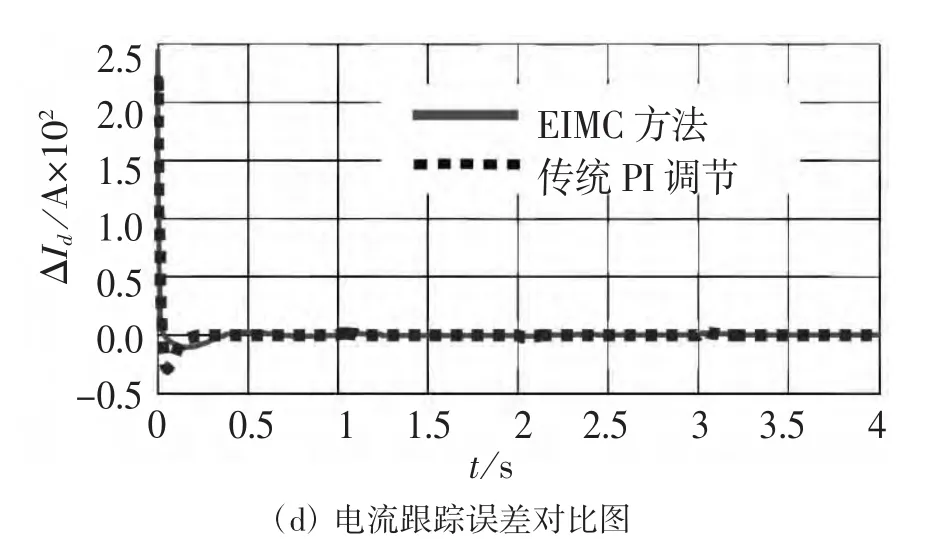
图5 路面坡度不断变化时仿真曲线

图6 反电动势和转矩系数扰动时仿真曲线

图7 温度升高时仿真曲线
由以上图形可以看出,EMIC控制方法,在3种情况下,速度和电流的过渡过程超调量、跟踪误差和跟踪时间均优于传统的PI控制方法。
6 结论
针对电动汽车恶劣的运行环境和复杂多变的控制系统模型,本文根据EIMC原理控制永磁无刷直流电机(PMBLDCM)提高电动汽车控制系统适应模型失配的能力。文中分析了增强型内模控制系统存在模型不确定性时的鲁棒性。通过互补灵敏度函数η(s)研究系统的鲁棒稳定性,并通过灵敏度函数ε(s)分析系统的品质鲁棒性。分析结果表明,通过调整滤波器的滤波时间可以使控制系统同时具有较强的鲁棒稳定性和较好的品质鲁棒性。为了增强电动汽车控制系统的鲁棒性,将EIMC方法应用于以永磁无刷直流电机(PMBLDCM)为动力的电动汽车控制系统的速度控制中。理论分析和仿真结果表明,在模型失配和负载扰动的情况下,EIMC可以提高电动汽车控制系统的鲁棒稳定性和品质鲁棒性。根据EIMC原理设计的速度控制器仅有一个调节参数,便于工程应用中在线调整。
[1]张 敏.电动车用永磁无刷直流电机驱动系统研究[D].华中科技大学,2012.
[2]Garcia C E,Morari M.Internal Model Control.1.A Unifying Review and Some New Results[J].Ind Eng Chen Process Des Dev,1982,21(2):308-323,3-5.
[3]J C Gonzalez-Gomez,J A Ruz-Hernandez,R Garcia-Hernandez,F Ornelas-Tellez.Real-Time Neuro-Fuzzy Control Based on Internal Model Applied to a DC Motor[C].World Automation Congress(WAC),2012,1-4.
[4]N Amuthan,P Subburaj,P Melba Mary.Direct Mo del Reference Adaptive Internal Model Controller for Better Voltage Sag Ride through in Doubly Fed Induction Generator WindFarms[J].ElectricalPowerandEnergySystems,2013,47:255-263.
[5]Gang Shen,Zhencai Zhu,Yu Tang,et al.Combined Control Strategy Using Internal Model Control and Adaptive Inverse Control for Electro-Hydraulic Shaking table[J].Journal of MechanicalEngineeringScience,2012,1-13.
[6]Gregor Gregorcic,Gordon Lightbody.Gaussian Process Internal ModelControl[J].International Journal of Systems Science,2012,43(11):2079-2094.
[7]刘和平,战祥真等.惯量自补偿的纯电动汽车动力系统模拟试验台研究[J].电机与控制学报,2011,15(10):56-57.
[8]焦晓红,李 帅.永磁同步电机驱动电动汽车速度自适应控制[J].电机与控制学报,2011,15(11):84-85.
[9]周 涌,陈庆伟,胡维礼.内模控制研究的新发展[J].控制理论与应用,2004,21(3):477-478.
[10]朱凤成.鲁棒控制与内模控制及其应用[D].北京化工大学,2002,19-20,10-12.
