钢结构建筑物磁场特征定量评估

郭成豹，刘大明

（海军工程大学电气工程学院，湖北武汉430033）

钢结构建筑物磁场特征定量评估

郭成豹，刘大明

（海军工程大学电气工程学院，湖北武汉430033）

为了研究钢结构建筑物的磁场特征，基于相似性定律制作了典型钢结构建筑物的磁性物理缩比模型。并进行了磁场测量试验，分离出了缩比模型的感应和永久磁性的磁场特征。基于缩比模型试验数据，建立了基于磁矩量法的钢结构建筑物磁场特征数学模型，并分析了其衰减特性。一座边长12 m的立方体钢结构建筑物磁场特征评估分析表明，在建筑物一侧0～100 m的地面上，其磁场特征幅值从6 400 nT迅速下降为0.005 nT，在建筑物周围100 m之外的区域产生的磁场已可忽略不计。本研究采用物理模型和数值模拟相结合的手段，实现了钢结构建筑物磁场特征的定量分析。该技术适用于磁测量设施周边建筑物干扰磁场的精确评估，具有较高实用价值。

电气工程；钢结构建筑物；缩比模型试验；磁场特征；磁矩量法

现代建筑物（例如楼房、桥梁、隧道等）大部分是由钢筋混凝土，甚至是钢结构组成的。这些建筑物在地磁场等因素的作用下，会被磁化从而在其周围空间产生显著的磁场特征。含有钢结构的建筑物产生的磁场特征会给多个行业造成影响。例如，磁场测定设施（例如，地磁台、舰艇消磁站等）周围存在的建筑物会严重干扰磁场的精密测量［1-4］；在地下工程探测、导航、军事等领域，可以利用建筑物钢结构产生的磁场特征进行探测、定位、导航等作业［5-8］；在医疗卫生领域，建筑物产生的磁场对人体健康存在潜在影响［9］。因此，急需对钢结构建筑物的磁场特征进行分析研究，以期得到一种钢结构建筑物磁场特征分布定量分析技术，便于对建筑物磁场特征进行开发利用以及消除。在建筑物磁场特征研究中，为了降低问题的复杂度，横梁、立柱等所用的型钢可被等效为同样或类似截面积的钢棒；管道、门窗等由于含铁磁材料较少而被忽略；钢筋混凝土结构、墙壁和楼板可被等效为同样体积的钢筋。同时，钢结构建筑物的磁性磁场与舰船磁场类似，存在2个主要组成部分：感应磁性磁场和永久磁性磁场。其中，感应磁性磁场是在地磁场作用下产生的感应效应，与地磁场的幅值和方向密切相关；永久磁性磁场是基本固定不变的磁性磁场分量，与建筑物钢结构的施工工艺、应力、磁性历史等因素相关。因此，钢结构建筑物的感应和永久磁性磁场是研究的2个重点。首先建立钢结构建筑物的磁性物理相似性条件，制作了一座典型钢结构建筑物的磁性物理缩比模型，进而开展磁场测量试验。然后，分析试验结果，分解得到建筑物磁场特征的感应磁场分量和永久磁场分量，并采用磁矩量法技术对感应磁场分量进行了数值建模分析。最后，采用数值分析技术综合评估分析了建筑物的磁场衰减特性。研究结果对于磁场检测设施建设、磁场导航、工程检测、军事等领域都具有重要的参考价值，具有广阔推广应用前景和显著效益。

1 相似性条件及磁性缩比模型构建

要建立钢结构建筑物的磁性物理缩比模型，需要遵循相似性定律。由于建筑物的钢结构绝大部分是梁、柱、杆等形式，因此主要针对这些钢棒形状建立相似性条件。

1）横截面积相似。如果缩比模型构件的横截面积为sm，横截面积相似表述为方程：

式中：sf为建筑物构件实体的横截面积，S为缩比因子。

2）磁导率×横截面积相似。如果缩比模型构件的横截面积为sm，磁导率为μm，那么它们的乘积可以表述为相似性方程：

式中：μf为建筑物构件实体的磁导率。

某典型钢结构建筑物为边长12 m的立方体，主体框架由型钢构成。按照1∶10的比例可以设计制作如图1、图2所示的缩比模型，模型长、宽、高均为1.2 m，由48根长1.2 m、直径10 mm的Q235钢筋捆扎而成。

图1 建筑物磁性物理缩比模型的照片Fig.1 Photograph of the ferromagnetic physical scale model of a building

图2 建筑物磁性物理缩比模型的示意图Fig.2 Schematic diagram of the ferromagnetic physical scale model of the building

2 磁性物理缩比模型磁场测量试验

为了测量缩比模型的磁场特征，在实验室构建了如图3所示的试验设施。缩比模型在x方向9 m的距离上移动，通过激光定位仪可以实时记录缩比模型的位置，而位于缩比模型正下方0.37 m处的一个三分量磁传感器同步测量出缩比模型的磁场特征。通过在磁北、磁南2个方向上的测量，可以分别得到2个磁场特征Bn和Bs，如图4、图5所示。进而得到纵向感应磁性的磁场特征：Bix＝（Bn-Bs）／2，如图6所示。

采用垂向地磁场模拟线圈，可以产生一个模拟的地磁场垂直分量。分别测量线圈通电前后的缩比模型磁场特征B0和Bc，可以计算得到缩比模型的垂向感应磁性的磁场特征：Biz＝Bc-B0，如图7所示。

当缩比模型处于磁北方向时，其磁场特征含有的分量为：Bn＝Bp+Bix+Biz，其中Bp为其永久磁性的磁场特征。可以计算得到缩比模型永久磁性的磁场特征：Bp＝Bn-Bix-Biz，如图8所示。

试验所在地的地磁场垂直分量为35 400 nT、水平分量为34 300 nT。从测量数据可以看出，缩比模型磁场特征中感应磁性约占1／4，永久磁性约占3／4，二者比例关系约为1∶3。

图3 磁场测量设施示意图Fig.3 Schematic diagram of the installation of magnetic field measurement

图4 缩比模型处于磁北方向时的磁场特征Fig.4 Magnetic signatures of the scale model in magnetic north

图5 缩比模型处于磁南方向时的磁场特征Fig.5 Magnetic signatures of the scale model in magnetic south

图6 缩比模型纵向感应磁性的磁场特征Fig.6 Magnetic signatures of the scale model＇s induced longitudinal magnetization

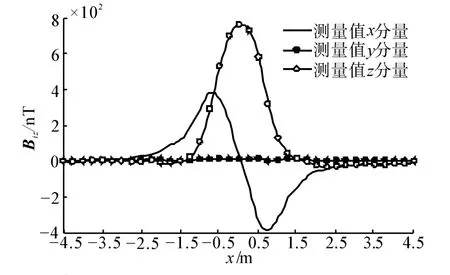
图7 缩比模型垂向感应磁性的磁场特征Fig.7 Magnetic signatures of the scale model＇s induced vertical magnetization

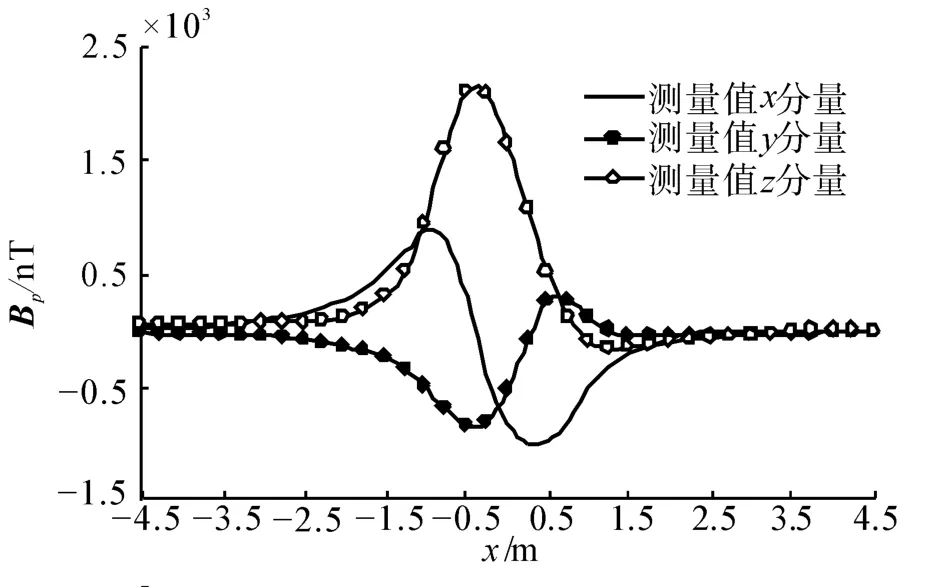
图8 缩比模型永久磁性的磁场特征Fig.8 Magnetic signatures of the scale model＇s permanent magnetization

3 磁场特征数值建模分析

3.1 数值建模方法

为了进一步分析钢结构建筑物的磁场特征，基于缩比模型试验数据，联合采用磁矩量法（magnetic moment method，MMM）和多层自适应交叉近似法（multilevel adaptive cross approximation）建立钢结构建筑物的数学模型。

一个铁磁物体，设其体积为V，处于磁化磁场H0中。整个空间中的磁场是磁化磁场H0和铁磁材料被磁化产生的磁场Hm的总和：

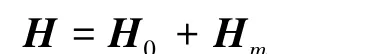
体积V内的磁化强度和空气区域的磁感应强度之间的关系为

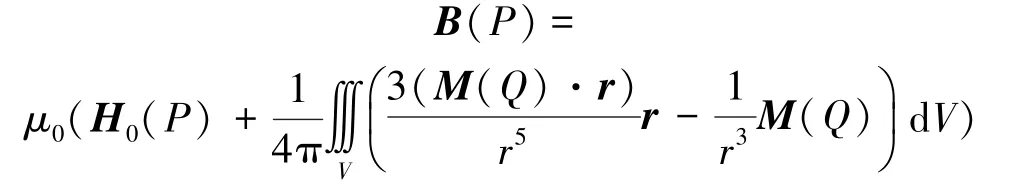
式中：μ0是空气区域的磁导率，P是空气区域内的一个点，Q是体积V内的积分点，r是PQ矢径，r是r的长度。将体积V划分为n个体积单元。磁矩量法实施过程中，可以根据具体情况采用不同的剖分单元，例如体单元、面单元、线单元等［10-11］，这里则采用线单元［12］。

铁磁材料的基本特性是它们吸引磁通的能力，对于直线细钢棒的情形，其直径相对于其长度的比率是相当小的，并且材料的磁导率比空气大得多，那么钢棒成为磁力线通道的现象会更加明显。在这种情况下，钢棒内的磁场可以被认为与钢棒直线方向相切。磁场的切向分量在钢棒的横截面上是恒定的，磁场H全部是切向分量的。

一个长度为l，横截面积为s的细钢棒线单元具有均匀的磁化强度M，在两端分别感应出点磁荷+q和 -q，（q＝Ms）。以2个点磁荷的联线为x轴，联线的中点为原点，取笛卡尔坐标系如图9所示。线单元在x，y平面上任一点P（x，y）处产生的磁场强度为

如将细钢棒构成的建筑物划分为n个单元，那么根据式（3）可以得到单元之间的相互作用系数。如图10所示，单元i的单位磁化强度在单元j的重心点处产生的切向磁场强度Gij。得到系数矩阵：

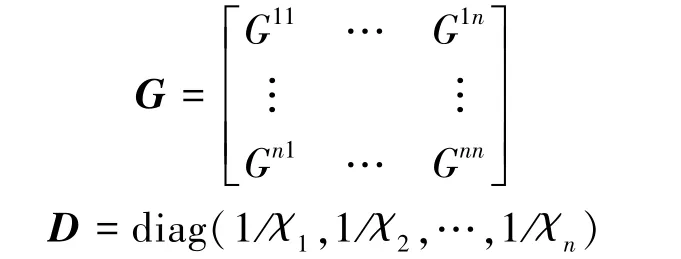
磁化强度未知数矩阵：

外部磁场矩阵：

最后得到所要求解的方程组：

求解上述方程可以得到磁化强度M。最后根据式（3）可以得到空间任意点处的磁场分布。

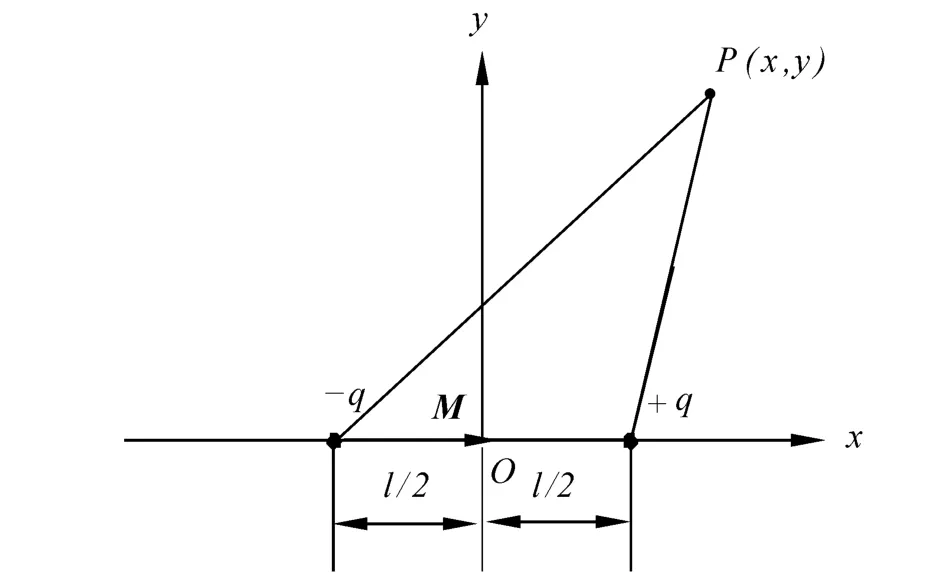
图9 细钢棒线单元的等效点磁荷分布Fig.9 Equivalent point magnetic charges of the line element

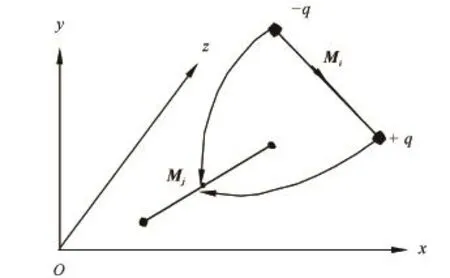
图10 线单元之间的相互作用Fig.10 The interaction of the two line elements

采用多层自适应交叉近似法算法对上述线单元磁矩量法得到的方程组进行快速求解［13-16］，在普通PC机上可以实现几十万个单元的大规模求解，可以满足绝大多数建筑物磁场分布特征的计算分析。

3.2 数值分析结果

将缩比模型的48根钢筋按照0.02 m的步长均匀划分为2 880个线单元。采用试错法调整钢筋的磁导率，使得缩比模型感应磁性的磁场特征计算值与测量值尽量接近，经过2～3次调整，二者之间差别可小于5%（如图11所示，缩比模型纵向感应磁性的磁场特征测量值与计算值高度吻合）。经计算，当钢筋的相对磁导率值设定为150时，缩比模型的纵向和垂向感应磁性的磁场特征的测量值和计算值都吻合得非常好。因此，后续分析计算中，设定钢筋的相对磁导率为150。

在地磁台、消磁站等低磁建筑物的建设过程中，需要考虑周围空间存在的建筑物产生的干扰磁场分布。在这种情形下，可以计算分析钢结构建筑物实体在其周围空间产生的磁场特征分布。如图12所示，磁场计算线位于建筑物北侧0～100 m范围内的地面上。计算该计算线上的建筑物感应磁性的磁场特征，并考虑永久磁性与感应磁性之间的比例系数1∶3，可以得到该计算线上建筑物的磁场特征总量分布，如图13所示，0～100 m的范围内，磁场幅值从6 400 nT迅速下降为0.005 nT。因此，该钢结构建筑物在周围100 m之外的区域产生的干扰磁场已可忽略不计。

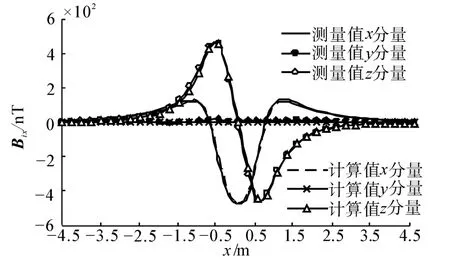
图11 缩比模型纵向感应磁场特征的测量值和计算值对比Fig.11 Comparison of the measured and calculated values of magnetic signatures of scale model＇s induced longitudinal magnetization

图12 建筑物北侧的磁场计算线（0～100 m）示意图Fig.12 Schematic diagram of the calculated line of magnetic signature in the northern side of building（0～100 m）

图13 建筑物北侧的磁场特征总量变化Fig.13 Change of the total intensity of magnetic signatures in the northern side of building

4 结论

综合采用缩比模型和数值分析技术，实现了钢结构建筑物磁场特征的精确评估。钢结构建筑物的缩比模型根据相似性定律建造，可以方便地在实验室进行磁场特征测量试验，并可分离出感应磁性和和永久磁性的磁场特征，尤其是可以在钢结构建筑物建造之前预先进行评估分析。而基于缩比模型试验数据，采用磁矩量法可以建立钢结构建筑物磁场特征的数学模型，推算出了钢结构的相对磁导率，并分析建筑物磁场特征衰减特性，并且可以根据简易缩比模型的实验数据进一步分析更复杂结构的钢结构建筑物的磁场特征。因此，所采用的缩比模型和数值分析相结合的技术手段可以方便地用于工程实际，具有较高的实用价值。

此外，所采用的技术也可以用于钢结构建筑物的非线性磁场分析，尤其是永久磁性分析，甚至可以推广应用于其他钢结构设施和设备（如机械设备、钻井平台等）的磁场分析，这将是下一步工作中的研究重点。

［1］赖加成，游永平，罗开奇.地磁台站建设中的材料磁性检测［J］.地震研究，2008，31（2）：155-159.

LAI Jiacheng，YOU Yongping，LUO Kaiqi.Magnetism test for the construction material of geomagnetic station［J］.Journal of Seismological Research.2008，31（2）：155-159.

［2］刘大明，郭成豹.非磁性建筑物空间磁场预测技术［J］.海军工程大学学报，2005，17（1）：32-36.

LIU Daming，GUO Chengbao.Prediction technique of space magnetic field of non-magnetic building［J］.Journal of Naval University of Engineering，2005，17（1）：32-36.

［3］YAMAZAKI K，KATO K，MURAMATSU K，et al.A practical method for evaluating magnetic disturbance due to buildings for the design of a magnetic testing site［J］.IEEE Transactions on Magnetics，2005，41（5）：1856-1859.

［4］ODAWARA S，HARAGUCHI Y，MURAMATSU K，et al.Magnetic field analyses of architectural components using homogenization technique［J］.IEEE Transactions on Magnetics，2010，46（8）：3313-3316.

［5］赵超，樊敬亮，周忠民，等.钢筋笼长度检测技术现状及展望［J］.地球物理学进展，2009，24（3）：1128-1135.

ZHAO Chao，FAN Jingliang，ZHOU Zhongmin，et al.Development and prospect of reinforcement cage length detection technology［J］.Progress in Geophys，2009，24（3）：1128-1135.

［6］蒲晓轩，董平，孙斌，等.灌注桩钢筋笼磁异常定量计算［J］.物探与化探，2009，33（4）：481-485.

PU Xiaoxuan，DONG Ping，SUN Bin，et al.Quantitative calculation of magnetic anomalies of steel bars in cast-in-situ piles［J］.Geophysical＆ Geochemical Exploration，2009，33（4）：481-485.

［7］王长利，刘代志.钢筋混凝土非实心圆柱体磁异常特征［J］.物探与化探，2005，29（1）：37-40.

WANG Changli，LIU Daizhi.Geomagnetic anomaly features of hollow ferroconcrete cylinders［J］.Geophysical＆ Geochemical Exploration，2005，29（1）：37-40.

［8］SUBBU P.Indoor localization using magnetic fields［D］.Denton：University of North Texas，2011：66-77.

［9］CvERMáKOVá E.Magnetization of steel building materials and structures in the natural geomagnetic field［J］.Acta Polytechnica，2005，45（6）：47-52.

［10］郭成豹，肖昌汉，刘大明.基于积分方程法和奇异值分解的磁性目标磁场延拓技术研究［J］.物理学报，2008，57（7）：4182-4188.

GUO Chengbao，XIAO Changhan，LIU Daming.Research on the continuations of magnetic field of magnetic object based on integral equation method and singular value decomposition［J］.Acta Physica Sinica，2008，57（7）：4182-4188.

［11］郭成豹，刘大明.薄钢壳物体磁特征建模研究［J］.兵工学报，2012，33（8）：912-915.

GUO Chengbao，LIU Daming.Modeling of magnetic signatures of thin-sheet objects［J］.Acta Armamentarii，2012，33（8）：912-915.

［12］GUO Chengbao，LIU Daming.Quantitative analyses of magnetic field distributions for buildings of steel structure［C］／／2012 Sixth International Conference on Electromagnetic Field Problems and Applications.Dalian，China，2012.

［13］BEBENDORF M.Approximation of boundary element matrices［J］.Numerische Mathematik，2000，86（4）：565-589.

［14］KURZ S，RAIN O，RJASANOW S.The adaptive cross approximation technique for the 3d boundary element method［J］.IEEE Transactions on Magnetics，2002，38（2）：421-424.

［15］ZHAO K，VOUVAKIS M N，LEE J F.The adaptive cross approximation algorithm for accelerated method of moments computations of EMC problems［J］.IEEE Transactions on Electromagnetic Compatibility，2005，47（4）：763-773.

［16］KATRIJN F，MARC V B.Solving a large dense linear system by adaptive cross approximation［J］.Journal of Computational and Applied Mathematics，2010，234（11）：3181-3195.

Quantitative evaluation of the magnetic signatures generated by steel structure buildings

GUO Chengbao，LIU Daming

（School of Electrical Engineering，Naval University of Engineering，Wuhan 430033，China）

In order to research the magnetic signatures generated by the steel structure buildings，a ferromagnetic physical scale model based on a typical steel structure building was made on the basis of the law of similarity.In addition，a measurement test was conducted at the magnetic fields，the magnetic signatures of the model＇s induced and permanent magnetizations were separated.Based on the test data of the scale model，a mathematical model of the steel structure building＇s magnetic signatures was established by applying the magnetic moment method，and the attenuation properties was analyzed.The evaluating results of the magnetic signatures generated by a cubic steel structure building with a side length 12 m showed that，on the ground 0 to 100 m away from one side of the building，the amplitude of the magnetic signatures decreased from 6 400 nT to 0.005 nT rapidly，while the magnetic signatures beyond 100 m away from the buildings was negligible.By combining the physical model and the numerical simulation results，the research realized a quantitative analysis of the magnetic signatures of the steel structural building.The technique is applicable for accurate evaluation of the magnetic distributions from a building around a magnetic measurement facility and the practical value is quite high.

electrical engineering；steel structure building；scale model test；magnetic signature；magnetic moment method

10.3969／j.issn.1006-7043.201305069

U665.18

A

1006-7043（2014）04-0493-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201305069.html

2013-05-27. 网络出版时间：2014-03-15 20：43：58

国家自然科学基金资助项目（51277176）.

郭成豹（1975-），男，讲师，博士.

郭成豹，E-mail：guochengbao＠gmail.com.