压力容器外部冷却两相自然循环特性理论分析

赵国志，曹欣荣，石兴伟

（哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001）

压力容器外部冷却两相自然循环特性理论分析

赵国志，曹欣荣，石兴伟

（哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001）

针对严重事故下压水堆压力容器下封头外侧与绝热层内侧环形通道内两相自然循环流动问题，利用FORTRAN语言，编写了压水堆压力容器外部冷却（external reactor vessel cooling，ERVC）一维稳态自然循环分析程序。通过分析不同摩擦系数的计算公式对两相自然循环质量流量和空泡份额计算的影响，与中国开展的REPEC（reactor pressure vessel external cooling）实验及RELAP5模拟结果对比，验证了程序的可行性。对ERVC系统重要的热工水力和结构参数进行了敏感性分析，得到结论：进口过冷度对ERVC系统内两相流量影响很大，当过冷度接近饱和值时，流量会出现峰值，进口面积、间隙宽度和水淹高度会影响质量流量峰值的大小；当过冷度高于峰值对应的过冷度，流量随过冷度增大而减小，反之随过冷度增大而增大。结果可为ERVC系统的设计和运行参数的评估提供了一种简便快速的方法。

ERVC；两相自然流动；一维稳态；质量流量；空泡份额；过冷度

压水堆在严重事故导致堆芯熔化后，压力容器外部冷却（external reactor vessel cooling，ERVC）是实现堆内熔融物滞留（in-vessel retention，IVR）的重要措施之一。其机理是压力容器下封头外侧与绝热层内侧环形通道内两相自然循环通过沸腾换热带走熔池的衰变热实现IVR，对IVR-ERVC的实验研究已有很多，其中一条重要结论是间隙内两相自然循环流动的顺畅性是决定IVR成败的重要因素，流量越大，压力容器下封头外壁的临界热流密度（critical heat flux，CHF）越大。

对于IVR-ERVC理论研究，西安交通大学开发的IVRASA分析程序主要针对熔池构型和其对下封头容器壁的传热［2］，对环形通道内两相自然循环流动并未予以考虑。本文在一维均相流模型的基础上，从稳态两相流动的质量、能量和动量守恒方程得到求解自然循环流速的方程，利用FORTRAN语言编程求解。计算结果与文献［3］中近期中国开展的REPEC（reactor pressure vessel external cooling）实验及RELAP5程序的模拟结果进行对比，并以AP1000结构为参考，对两相流动摩擦阻力计算关系式的敏感性和ERVC系统结构参数、热工水力参数对两相自然循环特性影响进行了分析，为ERVC系统的设计和运行提供一种简便快速的方法。

1 ERVC系统理论分析模型

1.1 系统概述

图1为ERVC自然循环示意图［4］。当堆腔水淹后，绝热层间隙内的水吸收下封头内熔池放出的热量而沸腾，由于浮力的作用，汽水混合物沿着绝热层环形通道向上流动，通过堆芯热段下方的出口排出，压力容器垂直段与绝热层间的环形空间相当于吸力筒，可增加两相自然循环流动的驱动压头。水蒸汽在安全壳空间内冷凝后流回安全壳内置换料水箱，与此同时，受热流体从间隙出口流进排水坑，最后通过节气阀流回堆腔，从而建立了对下封头外壁的长期自然循环冷却。

图1 ERVC系统示意图Fig.1 Schematic of ERVC system

1.2 ERVC两相自然循环一维稳态模型

ERVC系统工作压力为0.1～0.4MPa的低压环境，由于压力容器下封头与绝热层形成的朝向上的半球形流道内的两相流动受到离心力和重力是同向的，因此两相中较轻的一相是偏向下封头外壁一侧，形成了不对称流型，因此，均相流模型对于ERVC系统内两相流是一种简化处理。然而，本文寻求一种快速简便的计算ERVC系统内两相流量的方法，把ERVC系统内两相流仍近似用均相流模型进行计算。

对于一维均相流模型，其质量守恒、能量守恒方程可以写成

式中：ρ为密度，kg／m3；u为线速度，m／s；a为截面积，m2；G为质量流量，kg／s；h为焓，J／kg；q为加热功率，J／s；下标in为绝热层底部入口，c为绝热层内任意位置，out为加热段出口，TP为两相，l为单相液。

式（2）中hTP-hl＝χchlg+hsub，其中χc为质量含汽率；hlg为汽化潜热；hgs和hls分别为单相饱和汽焓和单相饱和水焓；hsub表示过冷焓，即hls-hl。

根据质量含汽率的定义，χc可以写成

动量守恒方程为

式中：等号右边第2项为摩擦压降梯度，第3项为形阻压降梯度，第4项为加速度压降梯度。

对绝热层内外整个流道进行积分，即

由于汽-液混合物离开加热段后，其两相密度在上升段不变［5］，且等于加热段出口混合物密度，则有质量守恒方程容易得知上升段内两相混合物和绝热层外侧流体线速度不变，于是，式（5）等号右边第1项对加热段、上升段和绝热层外侧3段分别进行积分并整理可得

上升段环形空间的两相平均密度为

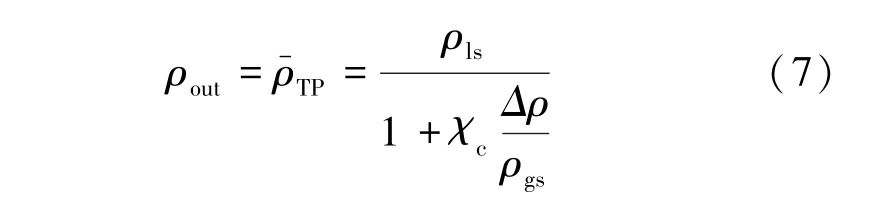
式中：ρls和ρgs分别表示饱和水和饱和汽密度，Δρ为饱和水、汽密度差。

把式（3）带入式（7），可以得到ρc和uc的关系，即

把式（8）带入式（3），可以得到χc与uc的关系，即

把式（9）带入式（6）整理可得

式（5）等号右边第2项摩擦压降和第3项形阻可以表示为

式中：f为摩擦系数；dH为通道当量直径，m；K为形阻系数；下标heat为加热段，up为上升段，down为绝热层外侧。式（11）等号右边1～3项分别为加热段、上升段和绝热层外侧摩擦压降和形阻压降，第4项为入口形阻压降。

把式（1）和（8）带入式（11），整理可得

式（12）中的摩擦系数fSP和fTP可应用麦克亚当斯关系式（13），科尔布鲁克公式（14），或者环形通道近似公式（15）计算，即

式中：ε为绝对粗糙度，m；D为直径，m。

根据Re的定义，单相和两相流动的Re为

式中：μ为动力粘度，kg／m·s；dH为水力直径，m。

两相平均动力粘度μ-TP为

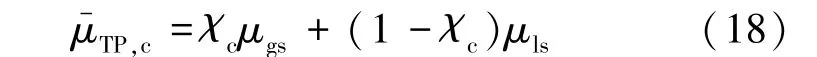
对于整个环路，式（6）等号右边第4项加速度压降为0，即

把式（10）、（12）和（19）带入式（5），整理得到关于uout的隐式方程，即

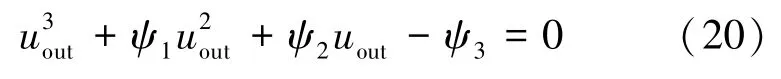
式中：

其中，

空泡份额的可用下式进行计算：

式中：υls和υgs分别为饱和液比容和饱和汽比容，m3／kg。

本文利用数值方法［6］，采用 FORTRAN语言，基于上述数学模型编写了计算ERVC两相自然循环流速的程序，其中迭代精度为10-4，通过解得的流速，根据式（9）和（24）等可以算出空泡份额等其他参数。

2 结果与分析

2.1 摩擦系数关系式的影响

分别选取式（13），当Re＞26.98（D／ε）8／7时调用式（14）前2式，当Re＞191.2／f0.5（D／ε）时调用式（14）的后式［7］和式（15）进行计算。从计算过程中看出，当选用式（14）进行迭代计算时，程序调用的全部是前2式。式（13）、（14）和（15）的计算结果见图2。

图2 摩擦系数计算公式的影响Fig.2 Effect of friction coefficient formulae

2.2 理论模型结算结果与实验和模拟数据的对比

2.2.1 理论模型计算结果与REPEC实验对比

REPEC实验由上海交通大学完成，实验与本文计算结果见图3。

图3 理论计算模型与REPEC实验结果对比Fig.3 Comparison between theory model and REPEC experiment results

实验采用全高度、全尺寸的切片实验装置，本文选取文献［3］中实验工况：下封头内壁加热功率为30%参考功率，在0.101 MPa时进口温度55℃（过冷度为 45 K），进口面积 0.005 30、0.008 84和0.017 67 m2，实验与本文计算结果见图3（a），对于3种不同的进口面积，本文计算结果与REPEC实验结果误差约为17.6%、23.6%、26%。实验工况为20%参考功率，进口面积为0.017 67 m2，进口温度为55～85℃（过冷度15～45 K），实验与文本计算结果见图3（b），过冷度为15、25、35和45 K时，本文计算结果比实验数据低22.9%，23.4%、23%和21.8%。2.2.2 理论模型计算结果与RELAP5模拟结果对比

文献［8］采用RELAP5计算了AP1000全尺寸ERVC系统在不同结构参数和热工水力参数下的质量流量，模拟结果与本文计算结果见图4。任意选取工况：熔池对下封头内壁加热功率为16 MW，在0.141 MPa下进口温度为360 K（过冷度约为22 K），进口面积为0.935和1.122 m2，水淹水位为 6和7.34 m，进口面积为0.935和1.122 m2时，本文计算结果比模拟结果低21.4%和23.1%；水淹水位为6和7.34 m时本文计算结果比模拟结果低28.7%和31%。

从与REPEC实验和RELAP5模拟结果的比较来看，质量流量的误差最高可达31%，尚在可接受的范围内，其误差可能来自于均相流模型与实际模型的差异、摩擦系数的经验公式、形阻损失系数的估计等。

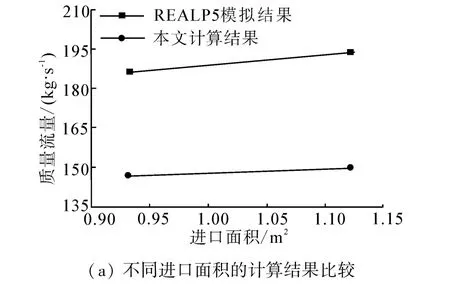
图4 理论计算模型与RELAP5计算结果对比Fig.4 Comparison between theory model and REALP5 computing results

总体来说，本程序基本可以估计大多数ERVC系统结构参数和热工水力参数对两相自然循环流量的影响趋势。

2.3 热工水力与结构参数的影响

2.3.1 进口水过冷度和加热功率的影响

事故初始时IRWST中水与安全壳内温度平衡，约为30℃，过冷度约为70 K。

在考虑10%不确定性后，AP1000熔池功率可达约50 MW［9］，图5给出了熔池功率对两相自然循环流量和空泡份额的影响。从图5（a）可以看出当过冷度高于峰值对应的过冷度时，自然循环流量随着过冷度的增大而减小，低于此过冷度时，自然循环流量随着过冷度的增大而迅速增大，这是因为当进口水的过冷度较高时，间隙内水以过冷沸腾为主，两相摩擦压降小，由下降段与上升段的密度差引起驱动压头主要用于克服形阻，因此随着过冷度增大，驱动压头减小，自然循环流量减小；当进口水的过冷度接近饱和值时，间隙内水剧烈沸腾，空泡份额很大，驱动压头大，过冷度升高，使蒸汽夹带的水滴增多从而使流量升高。功率为50、30、18、10和1 MW时，峰值对应的过冷度分别为10、6、3、2和1 K。

从图5（a）亦可看出，当加热功率大于10 MW时，若过冷度低于流量峰值对应的过冷度时，对于同一过冷度，自然循环流量随着功率的增大而减小，大于流量峰值对应的过冷度时，随着功率的增大而增大，这与文献［1］得出的结论是一致的，其主要原因是两相摩擦压降在过冷度高于峰值对应的过冷度时随着功率的升高而升高，低于此过冷度时随着功率的升高而减小。

同时从图5（a）还可以看出，当加热功率大于10 MW时，质量流量峰值的大小与加热功率基本是无关的，仅与压力、进口面积、间隙宽度和水淹水位等因素有关。功率的大小仅决定了质量流量峰值对应的过冷度大小，功率越大，峰值对应的过冷度越大。从图5（b）可以看出当过冷度较大时，空泡份额很低，间隙内水是以过冷沸腾的形式带走熔池的衰变热。

图5 加热功率对质量流量和空泡份额的影响Fig.5 Effect of heating power on mass flow rate and void fraction

2.3.2 压力的影响

AP1000安全壳的设计压力约为0.4 MPa［10］，因此计算选取的压力为0.101、0.141、0.202、0.303和0.4 MPa。当加热功率为30 MW时，压力对两相自然循环流量和空泡份额的影响见图6。

从图6（a）、（b）可以看出，只有当过冷度较低时压力对流量才有影响，当过冷度高于约10 K时，压力对质量流量不再敏感。从图6（c）、（d）可以看出，当过冷度低于10 K时，压力越高，空泡份额越大。

由于压力在流速计算公式中并未直接出现，其对流速的计算主要是通过影响流体密度、动力粘度等参数实现的。当过冷度较高时，间隙内以过冷沸腾为主，两相密度与下降段单相密度接近，由密度差引起的驱动力弱，单相摩擦压降随着过冷度的升高而增大；当过冷度较低时，空泡份额很高，见图6（c）、（d），由密度差引起的驱动力强，当压力较低时，两相摩擦压降的影响较压力较高时更明显，因此对于同一低过冷度值，其流量要低于压力较高时的流量。不同压力下，流量峰值对应的过冷度相差不大。

图6 压力对质量流量和空泡份额的影响Fig.6 Effect of pressure on mass flow rate and void fraction

2.3.3 进口面积的影响

加热功率为30 MW，压力为0.101 MPa，环形通道截面积为1.454 m2时，不同的进口面积值对两相自然循环流量和空泡份额的影响见图7。从图7很容易看出，过冷度高于20 K时，流量和空泡份额对进口面积的变化不再敏感；当过冷度低于20 K时，进口面积越大流量越大，空泡份额越小。随着进口面积的增大，峰值对应的过冷度逐渐趋近于0。

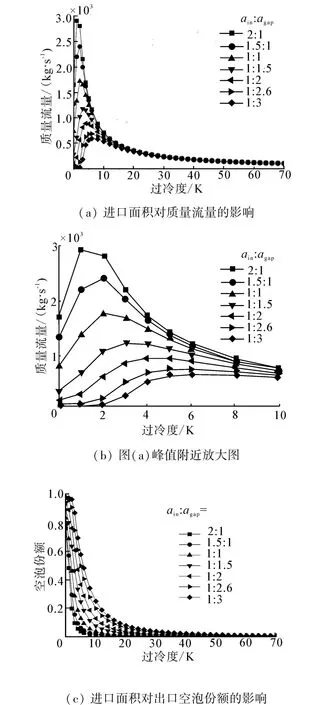
图7 进口面积对质量流量和空泡份额的影响Fig.7 Effect of inlet area on mass flow rate and void fraction

2.3.4 绝热层间隙宽度的影响

加热功率为30 MW，压力为0.101 MPa，进口面积为0.56 m2时，绝热层间隙宽度对两相自然循环流量和空泡份额的影响见图8。从图8（a）可以看出，当过冷度较高时，自然循环流量随着间隙宽度的减小而升高，当过冷度较低时，流量随着间隙的减小而降低，当间隙宽度大于0.2 m时，间隙宽度对自然循环流量的影响不大。随着间隙宽度的减小，峰值对应的过冷度升高。从图8（b）、（c）可以看出，当过冷度大于15 K左右时，间隙宽度对空泡份额的影响不大；当小于15 K左右时，间隙宽度大于0.1 m后，其对空泡份额的影响亦不大。

图8 间隙宽度对质量流量和空泡份额的影响Fig.8 Effect of width of gap clearance on mass flow rate and void fraction

2.3.5 水淹水位的影响

加热功率为30 MW，压力为0.101 MPa，进口面积为0.56 m2，绝热层间隙宽度为0.1 m时，水淹水位（仅改变图1中L的大小）对两相自然循环流量和空泡份额的影响见图9。从图9很容易看出，过冷度高于10 K时，流量和空泡份额对水淹水位的变化不再敏感；当过冷度低于10 K时，水淹水位越高流量越小，空泡份额越大，这是因为水淹水位越高，静水位压头越大。水淹水位的高低对峰值对应的过冷度没有太大影响，L为4.833 1和0.831 1 m时，质量流量的峰值也仅相差68 kg／s，约9.2%。

图9 水淹水位对质量流量和空泡份额的影响Fig.9 Effect of flooding level on mass flow rate and void fraction

3 结论

本文基于ERVC两相自然循环模型编写了一维稳态程序，理论模型计算的质量流量与实验、REALP5的计算结果最高相差31%，尚在可接受的范围内。利用本程序可简便快速的分析ERVC系统在不同的热工水力和结构参数下的自然循环流量、空泡份额等重要参数。同时获得如下结论：

1）采用麦克亚当斯、科尔布鲁克和环形通道经验公式计算的两相质量流量在较高过冷度时接近，在较低过冷度时，采用麦克亚当斯和科尔布鲁克公式计算结果接近。

2）过冷度对两相自然循环流量影响很大，当过冷度接近饱和值时，流量会出现峰值，峰值出现所对应的过冷度与功率、进口面积和间隙宽度有关。

3）压力和水淹水位对峰值对应的过冷度影响不大；进口面积、间隙宽度和水淹高度会影响质量流量峰值大小。

4）当过冷度高于峰值对应的过冷度，流量随着过冷度增大而减小，反之随着过冷度增大而增大。

［1］PARK J W.Analytical evaluation of two-phase natural circulation flow characteristics under external reactor vessel cooling［J］.Annals of Nuclear Energy，2009，36（11）：1668-1675.

［2］张亚培，秋穗正，田文喜，等.严重事故下熔融物堆内持留理论研究［R］.核反应堆系统设计技术重点实验室年报，2011：219-226.

ZHANG Yapei，QIU Suizheng，TIAN Wenxi，et al.Theoretical study on in-vessel retention during severe accident［R］.Annual Report of Key Laboratory of Nuclear Reactor System Design，2011：219-226.

［3］李飞，李永春，程旭.针对REPEC加热实验的RELAP5程旭模拟与分析［J］.原子能能科学技术，2012，46（7）：816-819.

LI Fei，LI Yongchun，CHENG Xu.Simulation and analysis on REPEC heating experimental mechanism［J］.Atomic Energy Science and Technology，2012，46（7）：816-819.

［4］THEOFANOUS T G，SALMASSI T，DINH T N.Limits of coolability in the AP1000-related ULPU-2400 configuration V facility［R］.Santa Barbara：University of California，2003.

［5］HA K S，CHEUNG F B，PARK R J，et al.Evaluations of two-phase natural circulation flow induced in the reactor vessel annular gap under ERVC conditions［J］.Nuclear Engineering and Design，2012，253：114-124.

［6］丁丽娟，程杞元.数值计算方法［M］.北京：高等教育出版社，2011：35-66.

［7］LEVY S.Two-phase flow in complex systems［M］.［S.l.］：Wiley-Interscience，1999：135-139.

［8］TAO J，TONG L L，CAO X W.A study on natural circulation flow under reactor cavity flooding condition in advanced PWR［J］.Journal of Power and Energy Systems，2011，5（3）：429-439.

［9］ESMAILI H，KHATIB-RAHBAR M.Analysis of in-vessel retention and ex-vessel fuel coolant interaction for AP1000.ERI／NRC-04-201［R］.Washington DC：Nuclear Regulatory Commission，2004：1-73.

［10］杨江，田文喜，苏光辉，等.AP1000冷段小破口失水事故分析［J］.原子能科学技术，2011，45（5）：542-545.

YANG Jiang，TIAN Wenxi，SU Guanghui，et al.Analysis of cold leg small break LOCA for AP1000［J］.Atomic Energy Science and Technology，2011，45（5）：542-545.

Theoretical analysis of the properties of the two-phase natural circulation of ERVC

ZHAO Guozhi，CAO Xinrong，SHI Xingwei

（Fundamental Science on Nuclear Safety and Simulation Technology Laboratory，Harbin Engineering University，Harbin 150001，China）

Focusing on the problem of two-phase natural circulation flow inside the loop-shape passage between the outside of the lower head of the reactor vessel and the inside of the insulator in times of severe accidents，an analysis program for one-dimensional steady-state natural circulation under the external reactor vessel cooling（ERVC）condition was done by utilizing the FORTRAN language.The effects of the calculation formulae of different friction coefficients on mass flow and void fraction of the two-phase natural circulation flow were studied.The results were compared with those obtained in the Chinese REPEC（reactor pressure vessel external cooling）experiment and the RELAP5 simulation，and the feasibility of the program was demonstrated.A sensitivity analysis was performed for the important thermal-hydraulic and configuration parameters of the ERVC system，and the following conclusion was obtained：The inlet subcooling has a significant impact on the two-phase flow in the ERVC system.When the subcooling becomes close to the saturated value，the flow will reach the peak value.The inlet area，gap width and flooding height will influence the flow peak value of the quality flow.When the subcooling is higher than the subcooling corresponding to the flow peak，the flow will decrease following the increase of the subcooling，and contrariwise，the flow increases as subcooling increases.These results may provide a simple and convenient method for assessing the design and operation parameters of the ERVC system.

ERVC；two-phase natural flow；one-dimensional steady-state；mass flow；void fraction；subcooling

10.3969／j.issn.1006-7043.201303026

TL364.4

A

1006-7043（2014）04-0437-08

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201303026.html

2013-03-11. 网络出版时间：2014-03-15 21：01：49.

核电厂严重事故安全审评关键技术研究合作资助项目（201301-WXHT-05-1）.

赵国志（1983-），男，博士研究生；曹欣荣（1965-），女，教授，博士生导师.

曹欣荣，Email：caoxinrong＠hrbeu.edu.cn.