有限元／间接边界元法求解浸水板振动特性

刘 城，洪 明，2，刘晓冰

（1.大连理工大学船舶工程学院，辽宁大连116024；2.大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024）

有限元／间接边界元法求解浸水板振动特性

刘 城1，洪 明1，2，刘晓冰1

（1.大连理工大学船舶工程学院，辽宁大连116024；2.大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024）

针对浸水板结构振动，考虑流体可压缩特性，利用间接边界元法计算附加质量矩阵，包含计算中奇异边界单元的处理。结合结构有限元法求解无限域浸水板的振动特性，通过编制的相应计算机程序，对浸水悬臂矩形平板进行了流体间接边界元与结构有限元耦合数值模拟；并对水下自由板进行了模态识别实验，实验结果验证了数值计算结果的可靠性。典型算例表明了流体介质改变了结构的动力特性，在低频段流体的可压缩性对结构的动力特性影响甚微；推导的流固耦合数值方法对研究浸水结构动力和声辐射研究有很好的参考价值。

有限元法；间接边界元法；浸水板；附加质量矩阵；矩形平板；固有频率；流体可压缩性；模态识别

当振动结构周围流体对结构振动的影响不可忽略时，称为强流固耦合问题，诸如关系到舰船结构的减振降噪性能。流固耦合工程上广泛遇到，但由于问题的复杂性，比如轻流体与重流体、可压与不可压流体以及系统振动频率的不同等，都会对耦合的物理分析模型有很大的差异。计算方法上也是包含解析、数值和实验，本文仅针对低频段强耦合流固耦合系统振动特性的边界元／有限元数值分析研究。

在低频阶段，流体介质对结构的作用可通过在结构运动方程中加入附加质量项来实现流体固体耦合［1-9］。附加质量的数值计算方法有很多种，如文献［5］利用有限元法对结构的附连水质量进行了研究，利用有限元法计算无界辐射声场时，必须人为的截断流体域，且计算量大；文献［6］和文献［7］利用直接边界元法（direct boundary element method，DBEM）求解浸水结构的附连水质量，但此方法只适用于水下封闭结构，对水下开口结构无法进行计算；对于无限大刚性障板中的板或者加筋板结构，可以通过Rayleigh积分来计算流体对结构的影响，但实际工程中水下结构多处于无限域或者具有自由液面的半无限域水域中，而非Rayleigh积分要求的具有刚性壁面的半无限域，所以该方法具有很大局限性；文献［8］通过经验公式并求解水下悬臂板的附加质量，从而求解结构的自振频率和振型，该方法只适合水下悬臂板结构，且对于不同的长宽比及厚宽比，悬臂板的附加质量计算公式还有所不同，因此该方法也具有很大的局限性。

间接边界元法（IBEM）是从直接边界元法（DBEM）推导而来，它以结构表面的压力差（双层势）和压力梯度差（单层势）为未知变量，能同时计算内场问题和外场问题，同时适用于无限域中的封闭和开口结构。间接边界元法的另一个优点是它是通过变分原理推导出系统方程，得到的系统矩阵是对称的，这种对称性使其能够更有效的与结构有限元法相结合。本文根据文献［9］利用FEM／DBEM计算水下封闭结构的固有频率的原理上，运用间接边界元法（IBEM）［10-11］推导在低频段任意浸水结构的附加质量阵的数值算法，并考虑流体的可压缩性对水下结构动力特性的影响［12］，通过编制 FORTRAN计算机程序，得到结构的附加质量阵，然后与基于有限元结构质量矩阵相叠加，实现了浸水结构系统的振动特性数值模拟，并进行了相关模态识别实验，数值计算结果与实验结果的对比验证了本文算法的准确性。

1 理论基础

1.1 间接边界元方程推导

设如图1所示结构处无限流体域中，S为结构浸水表面，S两侧均有流体域。若结构浸水表面存在振动时，结构的振动会引起周围流体介质的扰动，从而在流体域中将产生辐射压力场，而流体的扰动也会反过来影响结构的振动。对于无粘且可压缩流体，在线性小扰动的情况下，流体域中各点的压力p满足Helmholtz方程：

式中：p为计算场点声压，k＝ω／c定义为波数，其中ω为流体介质运动圆频率，c为声波在流体介质中的传播速度。在浸水振动结构表面，流体压力法向梯度与法向振动速度满足：

式中：n为结构浸水表面法向（如图1所示），vn为结构表面法向振动速度，ρ为流体介质密度。

图1 IBEM声场域及边界示意图Fig.1 Representation of acoustic domain and boundary of IBEM

利用格林公式，压力辐射域中Helmholtz微分方程（1）可转为振动结构边界上Helmholtz积分方程：

式中：S、Ω1和Ω2分别表示结构表面、外域和内域，Y为振动结构表面（源点），X为流体域中计算点（场点），对于无限域，G X，Y( )＝e-ikr／4πr为Y点处的基本解，r为源点到场点距离，C X()为影响系数，它与Y及结构表面光滑度相关。

方程（3）为直接边界元对应的外场问题边界积分方程，内场问题边界积分方程也有类似形式［9］。间接边界元是从直接边界元方程推导而来，它以结构表面的声压差（双层势）和声压梯度差（单层势）为未知变量，在边界表面两侧分别对内场问题和外场问题应用上述直接边界元内外场的Helmholtz边界积分方程，然后将两方程相加，即可得声场域内任意点的声压：

式中：σ为结构表面的法向压力梯度差（单层势），μ为结构表面的声压差（双层势），其表达式为

假设结构表面满足Neumann边界条件，由上述关系式，可得边界条件与未知量的关系为

定义如下泛函［10］：

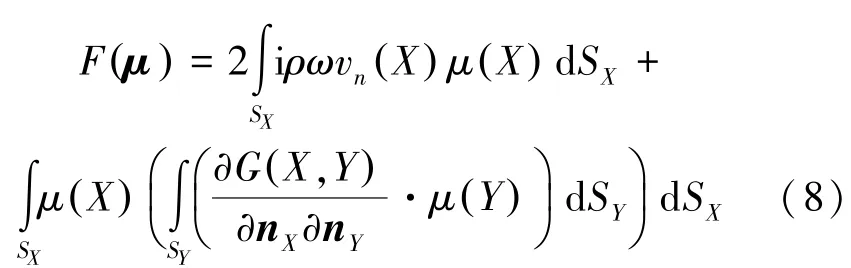
式中：泛函F（μ）具有超强奇异性，可通过下式改善其奇异性：

在边界上对方程（10）进行边界元离散，利用变分原理，即可得到系统方程，求解此系统方程可求出结构表面的声压差μ，然后利用式（4）即可求出流场中任意点的压力。

1.2 间接边界元方程的离散

本文以三结点三角形线性边界单元在流体固体耦合边界上对方程（9）进行数值离散，最终可得到如下形式的表达式：

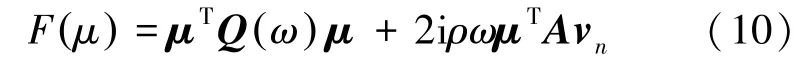
式中：Q（ω）为间接边界元的对称影响矩阵；μ为结构表面结点上的未知变量压力差列向量；A为结构表面流体单元面积矩阵。矩阵Q和矩阵A的单元块表达式如下：

利用变分原理，根据方程（15）可以得到间接边界元的表达式：

由此可以看出，影响矩阵Q（ω）为振动频率ω的函数，根据式（13）求出结构表面声压差后，任意点的压力由式（4）即可求得。

而对无粘、不可压流体，流体中声度c→∞，则k＝0，声场中任意点的压力p满足Laplace方程［12］：

与可压缩流体中的推导类似，流体的控制方程最终可写成

从上述推导中可以看出，可压缩流体与不可压缩流体中，最终得到的流体方程均可表达成式（16）的形式。需要注意的是，可压缩流体中的影响矩阵Q（ω）与频率有关，而不可压缩流体中的影响矩阵Q′与频率无关。

1.3 结构有限元与流体间接边界元耦合描述

考虑流体与结构振动的耦合影响时，结构振动方程的有限元形式为

式中：M为结构的质量矩阵；Cd为结构的阻尼矩阵；K为结构的刚度矩阵；u为结构有限元结点的位移向量，Fs为结构上作用外激励向量，Fa为结构与流体耦合面上流体作用在结构上流体动压力向量。

结构表面两侧均有流体介质时（如浸水非封闭结构），流体动压力可表示为

式中：T为方向余弦转换阵，A为结构表面流体单元面积矩阵，μ为结构表面结点压力差向量。

假设结构为简谐振动，则满足关系a＝iωv，v和a为结构振动的速度和加速度。流体变量和结构变量之间的几何关系如下：

方程（18）中的流体动压力项可以转化为

低频时忽略流体阻尼效应，流体动压力最终转化为结构的附加质量效应项：

根据前面的推导可知，可压缩流体中附加质量阵Ma与频率有关，而不可压缩流体中附加质量阵Ma与频率无关，在计算过程中需注意两者的区别。

计算出流体的附加质量阵后，水下结构流固耦合作用下的动力学方程的有限元形式变为

对应的广义特征值问题为

即

式中：Mc＝M+Ma为耦合的质量矩阵。

求解上述广义特征问题，即可求得浸水结构的固有频率和振型。

基于上述有限元和间接边界元理论，本文基于FORTRAN语言编写了相关的计算程序，其具体的程序流程如图2和图3所示。

图2 FEM／IBEM流固耦合动力分析主程序流程图Fig.2 Flow chart of the fluid-structure interaction dynamic analysis program

图3 IBEM计算附加质量阵子程序流程图Fig.3 Flow chart of the added mass matrix program

从流程图中可以看出，首先利用有限元知识构造结构的质量阵和刚度阵；然后利用间接边界元理论，根据式（21）得到结构的附加质量矩阵；最后将结构的附加质量阵和结构本身的质量阵相叠加，得到耦合的质量阵，然后求解广义特征值问题，计算出浸水结构的模态。

由间接边界元推导出的附加质量矩阵如式（21）所示，从式（21）的求解形式可以看出，附加质量矩阵是一个实数对称矩阵，且结构本身的质量阵也是一个实数对称矩阵，故耦合的质量矩阵为实数对称矩阵。为了与间接边界元耦合方便，结构有限元也是采用三角形三结点壳单元，在求得结构的刚度阵和耦合的质量阵后，即可求得结构的自振频率和振型，此类问题都可归结为求解形如式（24）所示的高阶广义特征值问题，本文应用子空间迭代法来求解此类广义特征值问题。

2 数值算例分析

对如图4所示的浸没于无限水域中的悬臂矩形弹性平板结构，平板长为0.406 4 m，宽为0.203 2 m，厚为2.67 mm，材料泊松比为0.3，杨氏模量为1.95× 1011N／m2，密度为7 700 kg／m3。分别将流体视为可压缩流体和不可压缩流体，比较流体的可压缩性对结构振动特性的影响。

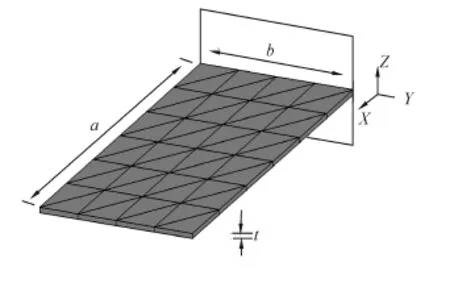
图4 矩形悬臂板单元剖分示意图Fig.4 Representation of mesh discretization for the cantilever plate

2.1 结构有限元与流体间接边界元耦合描述

假设流体不可压缩，流体的密度为1 000 kg／m3，浸水悬臂板前四阶固有频率如表1所示。

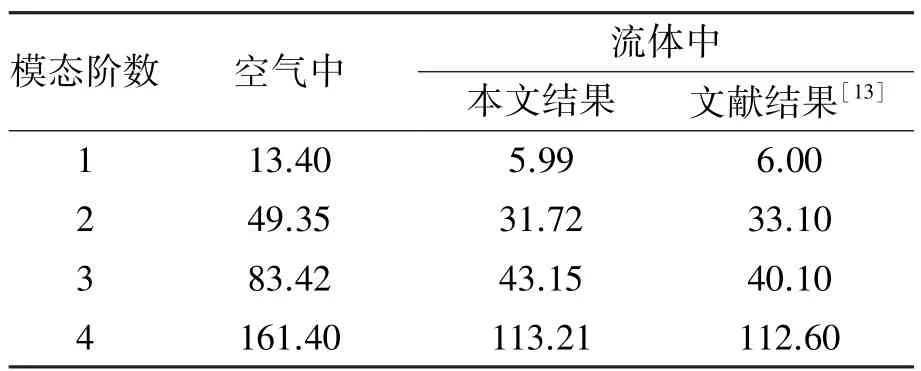
表1 空气与不可压流体中悬臂板固有频率计算结果Table 1 Natural frequency of the cantilever plate in theair and incompressible fluid Hz

从表1的计算结果可以看出，本文的计算结果与文献［13］的计算结果是相吻合的。

2.2 可压缩流体中悬臂板振动计算

从前面的理论推导中可知，在可压流体中结构的附加质量矩阵是振动频率的函数，在不可压流体中与计算频率无关。假设流体的密度1 000 kg／m3，声速1500 m／s，分别计算振动频率为10、100、500和1 000 Hz时结构的前四阶固有频率，计算结果如表2所示。

表2 可压缩流体中附加质量计算频率对固有频率的影响Table 2 Impact of the added mass matrix frequency on natural frequency of the plate in the incompressible fluid Hz

从计算结果可以看出，附加质量计算振动频率在低频范围内变化对结构的固有频率影响非常小，仅当增大到高频范围时才对结构的固有频率有较明显的影响。因此计算可压缩流体中板的固有频率时，低频段附加质量计算频率的大小对结果影响不大。

2.3 流体可压缩性对结构动力特性的影响

将流体分别视作可压缩与不可压缩2种模型下计算出的板的各阶固有频率进行对比，考虑流体的可压缩性对结构动力特性的影响，表3分别给出了结构在空气中、不可压流体和可压流体中的前四阶固有频率对比，其中可压流体中附加质量阵计算频率为10 Hz，计算结果如表3所示。

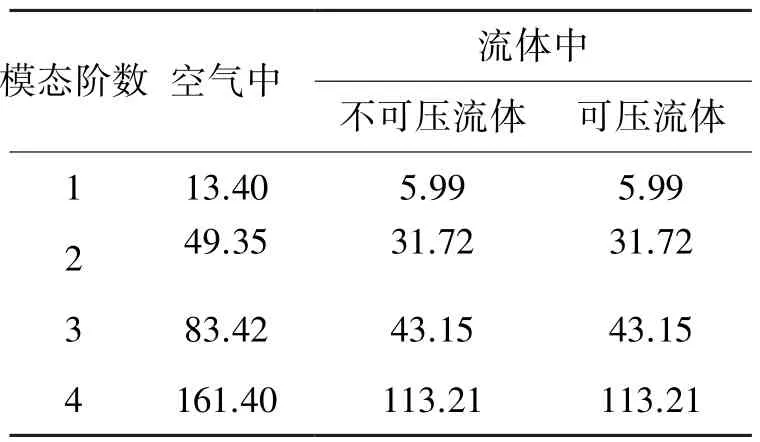
表3 流体可压缩性对固有频率的影响Table 3 Impact of fluid compressibility on the structure natural frequency Hz

从表3结果可以看出，结构在不可压缩与可压缩流体中的计算结果相差非常小，流体的可压缩性对结构的固有频率影响极其微小。因此可以说，在分析结构流固耦合自由振动频率时，可以忽略流体的可压缩性对结构固有频率的影响。

3 实验研究

为验证本文所推导的流固耦合数值方法与所编写程序的正确性，本文对水下全自由矩形钢板进行了模态识别实验，实验证明了数值计算结果的可靠性。

3.1 实验模型与仪器简介

本实验采用的是一块长为0.6 m、宽为0.25 m、厚为2.0 mm的矩形钢板。为模拟出无限大水域的自由场环境，该实验在消声水池中进行，消声水池采用长470 mm、底径直径50 mm的橡胶尖劈密排，可用空间为7.0 m×4.5 m×4.0 m。实验测量的主要仪器有东华DH5922动态信号测试分析仪、YE1311扫频信号发生器、JZK系列激振器和ICP加速度传感器。在实验过程中，用4根弹簧吊起矩形钢板放入消声水池中，这样可以模拟钢板的全自由边界条件，实验示意图如图5所示。

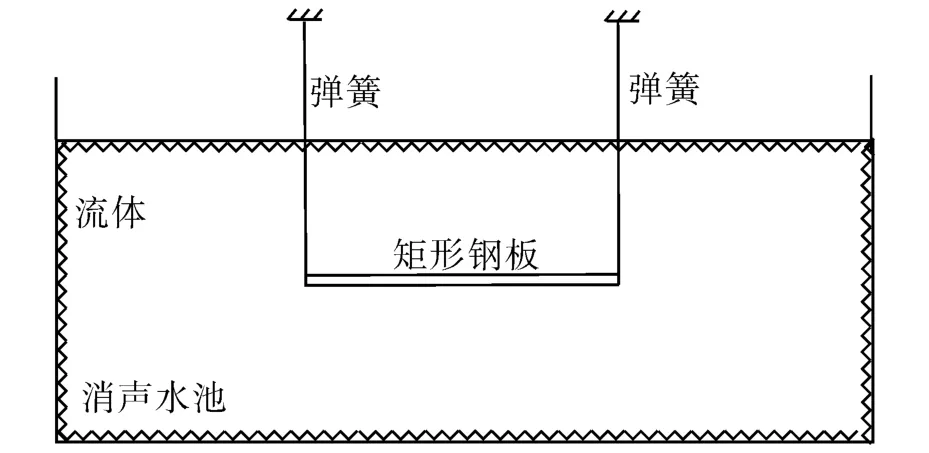
图5 水下自由板模态识别实验示意图Fig.5 Representation of modal identification experiment for the free submerged plate

3.2 实验模型的数值分析

运用本文编写的流固耦合动力分析程序来计算矩形钢板的自由模态，计算中取材料泊松比为0.3，杨氏模量为2.1×1011N／m2，密度为7 850 kg／m3；消声水池中水介质视为可压缩流体，密度为1 000kg／m3，水中声音传播速度为1 500 m／s；附加质量阵计算频率取为10 Hz，钢板的单元剖分示意图如图6所示。

图6 矩形平板单元剖分示意图Fig.6 Representation of mesh discretization for the rectangular plate

3.3 模型的实验测量

本实验在消声水池中进行。实验测量中，用4根弹簧吊起钢板放入消声水池中，采用激振器作为激励源，钢板上布置了15个加速度传感器，传感器的布置示意图如图7所示。

图7 水下自由板模态识别实验模型实物图Fig.7 Model of modal identification experiment

3.4 结果对比

对实验模型进行了耦合模态数值分析和模态识别实验后，两者得到的结果如表4所示。

表4 空气中与水中自由板前三阶固有频率实验值与数值解对比Table 4 Natural frequency of the free plate in the air and in the water

从表4结果可以看出，运用本文所推导的方法计算得到的结构振动模态结果与实验结果是相吻合的。说明本文推导的计算方法与所编写程序的正确性。图8表示的是空气中和水中全自由钢板的前3阶振型，从图中可以看出，由于流体附加质量的影响，减小了结构的固有频率，但对结构的振型影响很小。

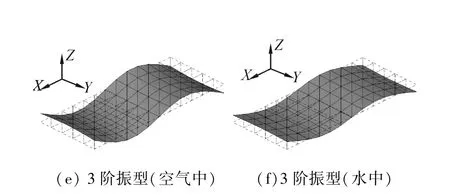
图8 空气中和水中全自由矩形钢板的前三阶振型Fig.8 The first three mode shapes in the air and water

4 结论

本文在间接边界元理论下，推导出低频段水下结构的附加质量矩阵，编写相应的FEM／IBEM流固耦合动力分析程序，考虑流体的可压缩性对结构动力特性的影响，分析了水下悬臂矩形平板的动力特性；并针对水下全自由矩形钢板进行了模态识别实验，得到如下结论：

1）本文的间接边界元求解附加质量的方法简单有效且具有可靠的精度，并为求解水下结构物的振动模态提供了一定的依据。本文方法的最大优点是能同时计算内场和外场问题，适合无限域中任意形状的复杂结构；

2）在低频段，流体对结构的影响可以忽略流体阻尼的影响，仅考虑流体的附加质量效应，及将流体作用简化为结构的附加质量项；而随着频率的增大，流体的附加质量效应减小，流体的阻尼作用增大，此时不能忽略流体阻尼作用的影响；

3）在低频段，流体的可压缩性对结构振动模态的影响甚微，在计算中可以忽略流体可压缩性对结构振动模态的影响。

［1］钱勤，黄玉盈，刘忠族.求附连水质量的一种直接方法［J］.力学与实践，1996，18（5）：19-21.

QIAN Qin，HUANG Yuyin，LIU Zhongzu.A direct solution method for the add water matrix［J］.Mechanics and Practice，1996，18（5）：19-21.

［2］王基盛，杨庆山.流体环境中结构附加质量的计算［J］.北京交通大学学报，2003，27（1）：40-43.

WANG Jisheng，YANG Qingshan.Calculation of add mass matrix of submerged structure［J］.Journal of Beijin Jiaotong University，2003，27（1）：40-43.

［3］王基盛，杨庆山，武岳，等.薄膜结构附加质量的计算方法［J］.空间结构，2003，9（3）.38-41.

WANG Jisheng，YANG Qingshan，WU Yue，et al.Calculation of add mass matrix of thin plate structure［J］.Space Structure，2003，9（3）：38-41.

［4］苏海东，黄玉盈.求半无限域流场中附连水质量的一种简便解法［J］.华中科技大学学报：城市科学版，2003，20（4）：14-16.

SU Haidong HUANG Yuying.Novel numerical method for solving added mass of structure embedded in semi-infinite liquid field［J］.Journal of Huazhong University of Science and Technology：Urban Science Edition，2003，20（4）：14-16.

［5］金占礼，王宗利，李红云，等.结构在无限流体域中振动时附连水质量的数值计算方法［J］.上海交通大学学报，2000，34（8）：1079-1082.

JIN Zhanli，WANG Zongli，LI Hongyun，et al.Numerical calculation method of the add water mass of vibratory structure in infinite fluid domain［J］.Journal of Shanghai Jiao Tong University，2000，34（8）：1079-1082.

［6］安小同，洪明，李艮田.基于FEM／BEM计算浸水结构振动特性［J］.船海工程，2011，40（6）：55-58.

AN Xiaotong，HONG Ming，LI Yintian.Calculation of vibration characteristics of submerged plates based on FEM／BEM［J］.Naval Architecture and Ocean Engineering，2011，40（6）：55-58.

［7］李华东，朱锡，罗忠，等.附连水质量的边界元法求解［J］.海军工程大学学报，2009，21（2）：45-49.

LI Huadong，ZHU Xi，LUO Zhong，et al.Calculation of the added water mass based on boundary element method［J］.Journal of Naval University of engineering，2009，21（2）：45-49.

［8］LIANG Chochung，LIAO Chingchao，TAI Yuhshiou，et al.The free vibration analysis of submerged cantilever plates［J］.Ocean Engineering，2001，28（9）：1225-1245.

［9］EVERSTINE G C.Prediction of low frequency vibrational frequencies of submerged structures［J］.Journal of Vibration and Acoustics，1991，113（2）：187-191.

［10］ALIA A，SOULI M，ERCHIQUI F.Variational boundary element acoustic modelling over mixed quadrilateral-triangular element meshes［J］.Communications in Numerical Methods in Engineerging，2006，22（7）：767-780.

［11］WANG Weiping，ATALLA N.A numerical algorithm for double surface integrals over quadrilaterals with a 1／R singularity［J］.Communications in Numerical Methods in Engineerging，1997，13（11）：885-890.

［12］张升明.流体的可压缩性对弹性结构振动的影响［J］.水动力学研究与进展，1994，9（4）：429-436.

ZHANG Shengming.The impacts on vibration characteristics of submerged structures of fluid compressibility［J］.Journal of Hydrodynamics，1994，9（4）：429-436.

［13］JEANS R A，MATHEWS I C.Solution of fluid-structure interaction problems using a coupled finite and variational boundary element technique［J］.J Acoust Soc Am，1990，88（5）：2459-2466.

The solution for vibration characteristics of submerged plates by applying FEM／IBEM

LIU Cheng1，HONG Ming1，2，LIU Xiaobing1

（1.School of Naval Architecture Engineering，Dalian University of Technology，Dalian 116024，China；2.State Key Laboratory of Structure Analysis for Industrial Equipment，Dalian University of Technology，Dalian 116024，China）

With a focus on the structural vibration of a submerged plate and consideration for the compressibility of fluid，the added mass matrix was calculated by utilizing the indirect boundary element method（IBEM）in this paper，including the treatment for the singularity boundary element in the calculation.In combination with the finite element method（FEM）for structure，the vibration characteristics of a submerged plate in the infinite fluid field were calculated.Through the use of corresponding programming，a numerical analysis of the coupling between the indirect boundary element of the fluid and the finite element of the structure was conducted for the submerged cantilever rectangular plate；in addition，a mode identification experiment was conducted on the underwater free plate.The experiment results verify the reliability of the numerical calculation results.The typical numerical example shows that the fluid medium changed the dynamic characteristics of the structure.At a low frequency band，the compressibility of the fluid had little impact on the dynamic characteristics of the fluid.The deduced numerical method for the fluid-structure coupling has excellent reference value for the dynamic research on a submerged structure and the research on acoustic radiation.

finite element method；indirect boundary element method；submerged plate；added mass matrix；rectangular plate；natural frequency；fluid compressibility；modal identification

10.3969／j.issn.1006-7043.201303052

O326

A

1006-7043（2014）04-0395-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201303052.html

2013-03-21. 网络出版时间：2014-03-15 20：44：29.

国家自然科学基金资助项目（51079027）.

刘城（1987-），男，硕士研究生；洪明（1959-），男，教授，博士生导师.

洪明，E-mail：mhong＠dlut.edu.cn