水声阵列信号处理对角减载技术

赵安邦，周彬，宋雪晶，毕雪洁

（哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001）

水声阵列信号处理对角减载技术

赵安邦，周彬，宋雪晶，毕雪洁

（哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001）

针对独立高斯白噪声背景和多个平面波干扰，尤其是低输入信噪比的情况，提出一种基于阵列信号协方差矩阵对角减载的波束形成技术。通过足够多次快拍的估计，得到接收信号稳定的协方差矩阵，对协方差矩阵进行适量的对角减载能提高阵列输出增益以及多目标的分辨能力。对基于对角减载的常规波束形成和最小方差无畸变波束形成器的阵列增益进行了仿真，分析了阵列增益随减载系数的变化关系，并研究了多目标分辨时对角减载系数的取值区间，最后仿真验证了对角减载技术提高MVDR多目标分辨能力的有效性。

对角减载；多目标分辨；阵列增益；最小方差无畸变响应；常规波束形成；阵列信号

随着制造工艺和激光校准技术的发展，声呐中的舷侧直线阵、鼻艏圆柱阵等阵元位置固定的水声信号接收阵列，其阵元位置已达到足够高的精度以至于可以忽略阵元位置误差对阵列波束形成产生的影响。而高性能信号处理平台的计算能力可以满足空间扫描间隔更小的波束输出，从而大大减小由于扫描间隔较大引起的导向矢量与目标真实方位不匹配所带来的阵列增益等性能的下降［1］。且针对静止或者相对运动缓慢的目标，可以通过增加积分时间，估计出更加准确的接收信号协方差矩阵。本文的研究均是在阵列接收信号协方差矩阵的估计足够准确的前提下开展的。

多重信号分类算法（multiple signal clsssification，MUSIC）［2-3］和旋转子空间不变算法（estimation of signal parameters via rotational invariance techniques，ESPRIT）［4-5］以及相关演变算法等高分辨率波束形成技术都要求有较高的输入信噪比。而水声阵列信号处理环境的输入信噪比较低［6］，所以目前在水声领域仍常用常规波束形成器（conventionalbeamforming，CBF）或者最小方差无畸变响应波束形成器（minimumvariancedistortionlessresponse，MVDR）［7-9］等阵列信号处理手段。

目前大部分阵列信号处理都是对相关矩阵进行某种运算，以便能优化提取目标信息，本文提出基于对角减载的阵列信号处理处理技术，将减少协方差矩阵中的噪声分量，提高声呐系统的阵列增益和多目标分辨能力。尤其对于水声通信网络［10］等水声传感器节点位置相对固定的应用领域，对于由多个传感器组成接收阵列的基站型节点，使用所提方法能增加基站接收节点的个数，降低通信误码率，从而提高整个网络的通信效率，具有一定的研究价值和应用前景。

1 基于对角减载的CBF波束形成器

常规波束形成器是独立高斯白噪声背景下的最佳波束形成器，考虑单个平面波入射，水平直线水听器阵列由N个阵元组成，t时刻阵列的输出如下

式中：A( θs)为入射平面波的方向矢量；θs为平面波水平入射角；X( t)＝[x(t)，x(t)，…，x(t)]T12N是t时刻阵列各阵元的输出信号；s( t)为入射平面波信号；N( t)＝[n1(t)，n2(t)，…，nN(t)]为阵列各阵元接收噪声，得到CBF波束形成的输出如下

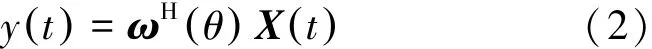
式中：ωHθ()＝ω1θ()，ω2θ()，…，ωNθ() [ ]H称为CBF波束形成权矢量。波束形成输出的平均功率为

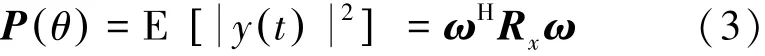
式中：Rx＝E[X( t)X( t)H]是阵列输出的协方差矩阵，展开后如下

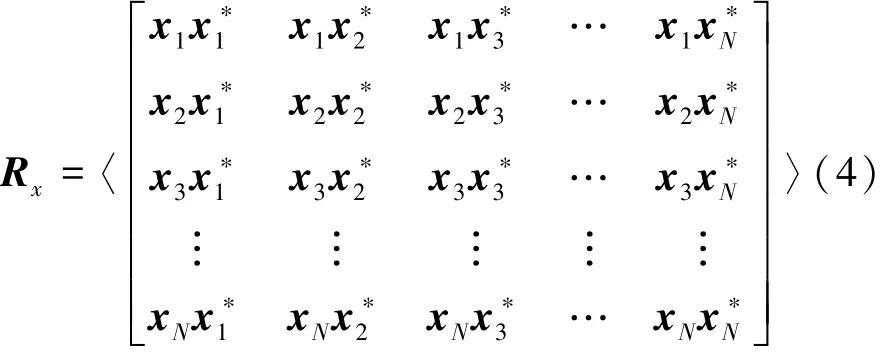
式中：〈*〉表示时间平均。在低信噪比条件下，当背景噪声满足独立各向同性高斯分布时，则有〈nin*j〉＝0。于是协方差矩阵中非主对角线元素噪声影响为零，而式（4）的主对角项信噪比较低。

为了提高主对角线项的信噪比，定义λ（0≤λ≤1）为协方差矩阵主对角线项减载系数，得到减载后的协方差矩阵如下

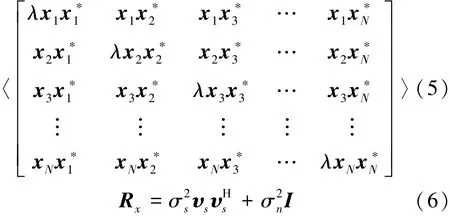
建立理想协方差矩阵模型如式（6）所示，其中σ2s为信号功率，为噪声功率，则输入信噪比SNRi＝10lg()，由CBF波束形成器可以得到ωCBF＝υk／N，υk为CBF导向矢量。阵列满足二分之一波长布阵，目标信号方位为90°，输入信噪比为－15 dB，分别使用理想噪声协方差矩阵和满足N( 0，)分布的仿真噪声进行CBF波束输出如图1所示。高斯白噪声仿真参数为采样率fs＝48 kHz，信号长度T＝1 s，阵元个数N＝8。

图1 SNRi＝－15 dB时目标方位为90°的CBF波束输出图Fig.1 CBF beam output when the target bearing is 90°（SNRi＝－15 dB）

从图1可以看到随着λ变小，CBF的输出波束变窄，旁瓣变低，说明基于对角减载技术的CBF阵列增益发生了变化。设CBF信号输出功率为Ps＝，噪声输出功率为Pn＝，其中ρn为阵列输入噪声的归一化协方差矩阵。对角减载后得到λ－1()I，＝λI。

定义阵列输出增益G如下

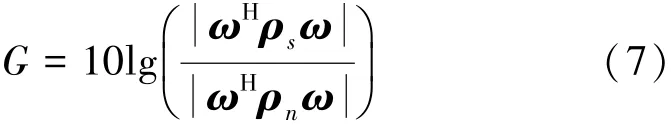
下面使用Monte Carlo法进行信噪比增益的仿真，仿真参数同图1，CBF在目标方位上的阵列增益如图2所示。

图2 SNRi＝－15 dB时CBF在目标方位上的阵列增益Fig.2 CBF array gain in target bearing when SNRi＝－15 dB

2 基于对角减载的MVDR波束形成器

使用Lagrange乘子法求得协方差矩阵对角减载后的最优权为，为Rx对角减载后的矩阵。

2.1 单个平面波干扰

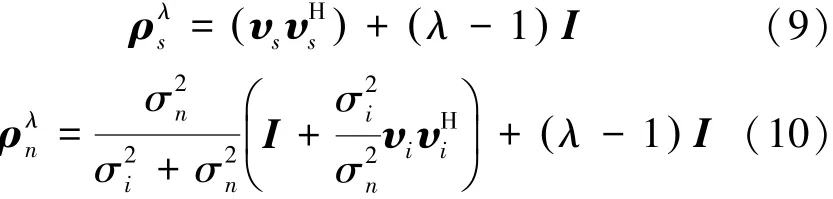
由无畸变响应定义得ωHλυs＝1，将式（9）代入Ps＝。使用Sherman-Morrison公式：

如下

由

得到基于对角减载的MVDR阵列增益如下

定义阵列输入干扰噪声比为LNRi＝10lg(／)，目标方位为90°，干扰方位为80°时，其余仿真参数同图1，阵列增益随减载系数变化的理论和仿真对比曲线如图3所示。如图3（a）当LNRi＝0时，在λ＝1／2处产生最大值，从图3（b）中可以看出，在λ＝2／3处产生最大值。

图3 单目标干扰时基于对角减载的MVDR阵列增益变化曲线Fig.3 MVDR array gain variation curve based on diagonal reduction when single disturbance

2.2 多个平面波干扰

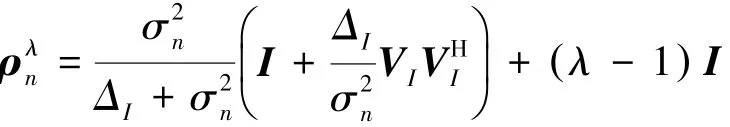
使用Woodbury公式：

进行ρλn的求逆运算。令：得到存在多个平面波干扰时，基于对角减载的MVDR波束形成器的阵列增益如下

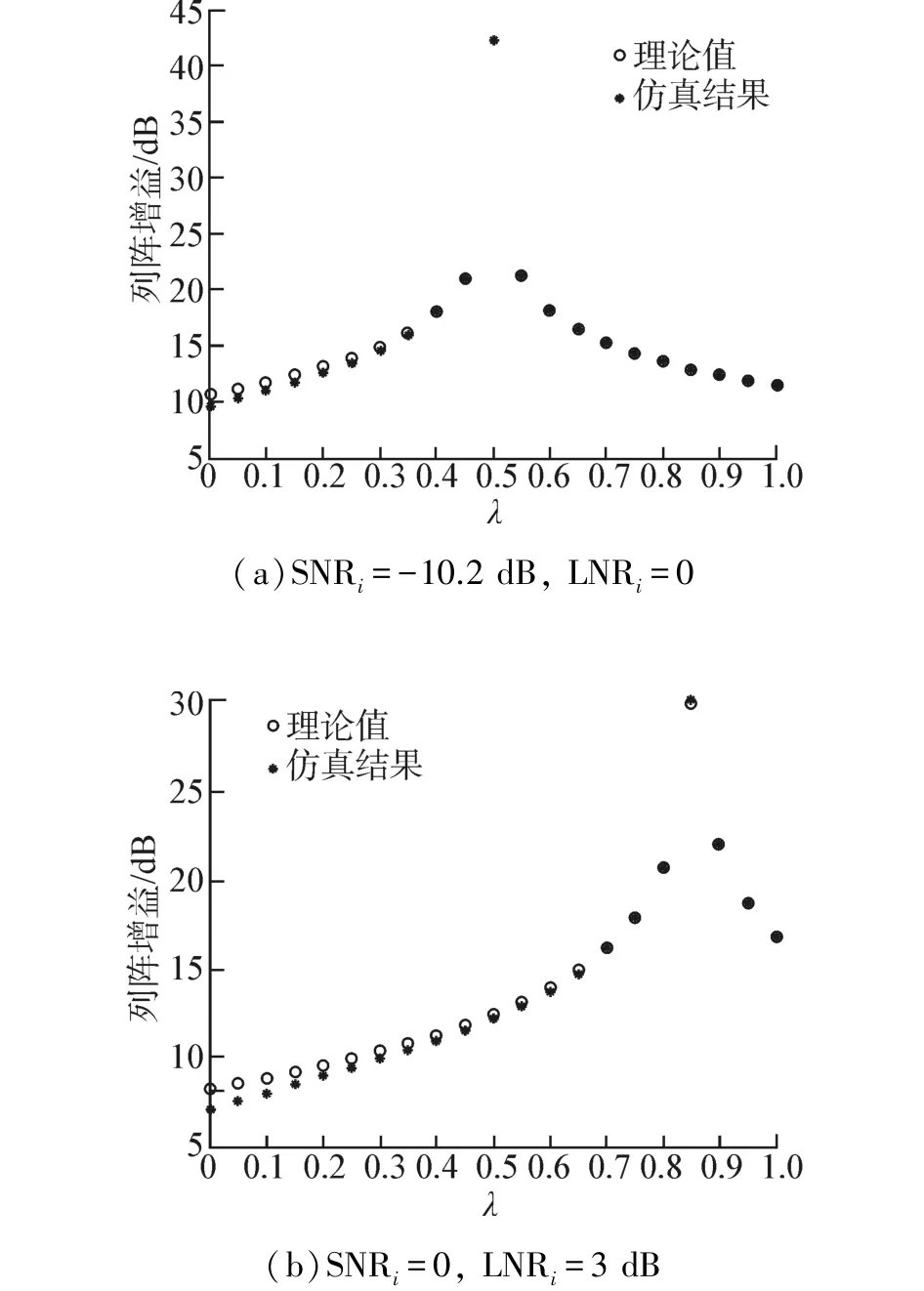
图4 多目标干扰时基于对角减载的MVDR阵列增益变化曲线Fig.4 MVDR array gain variation curve based on diagonal reduction when multiple disturbances

3 基于对角减载的MVDR分辨能力仿真

由上述理论推导和仿真结果可以看出，当尽可能减少接收信号协方差矩阵对角线元素上的噪声功率分量时，目标方向的阵列增益最高。由于MVDR是针对存在噪声场时接收平面波信号的情况下推导出的最优波束形成器，若把噪声完全减载后，会带来协方差矩阵不可逆等算法的不稳定性。若以λm表示协方差矩阵中背景噪声分量完全减载所对应的减载系数，则使用对角减载进行MVDR波束形成时，对角减载系数的取值范围应满足λm≤λ≤1。

首先仿真2个方位上等目标强度的分辨能力，处理过程直接对接收信号的协方差矩阵进行波束形成，所以对角线上元素除了干扰和噪声分量还包括信号分量。采用图1所示的仿真参数，得出不同信噪比下80°和90°方位上分辨能力仿真结果由图5所示。从图5（a）可以看到当＝＝时，对角线上的噪声分量约为1／3，所以当λ＝0.67分辨效果最好，同理当＝＝时，λ＝0.5的分辨效果最好，如图5（b）所示。

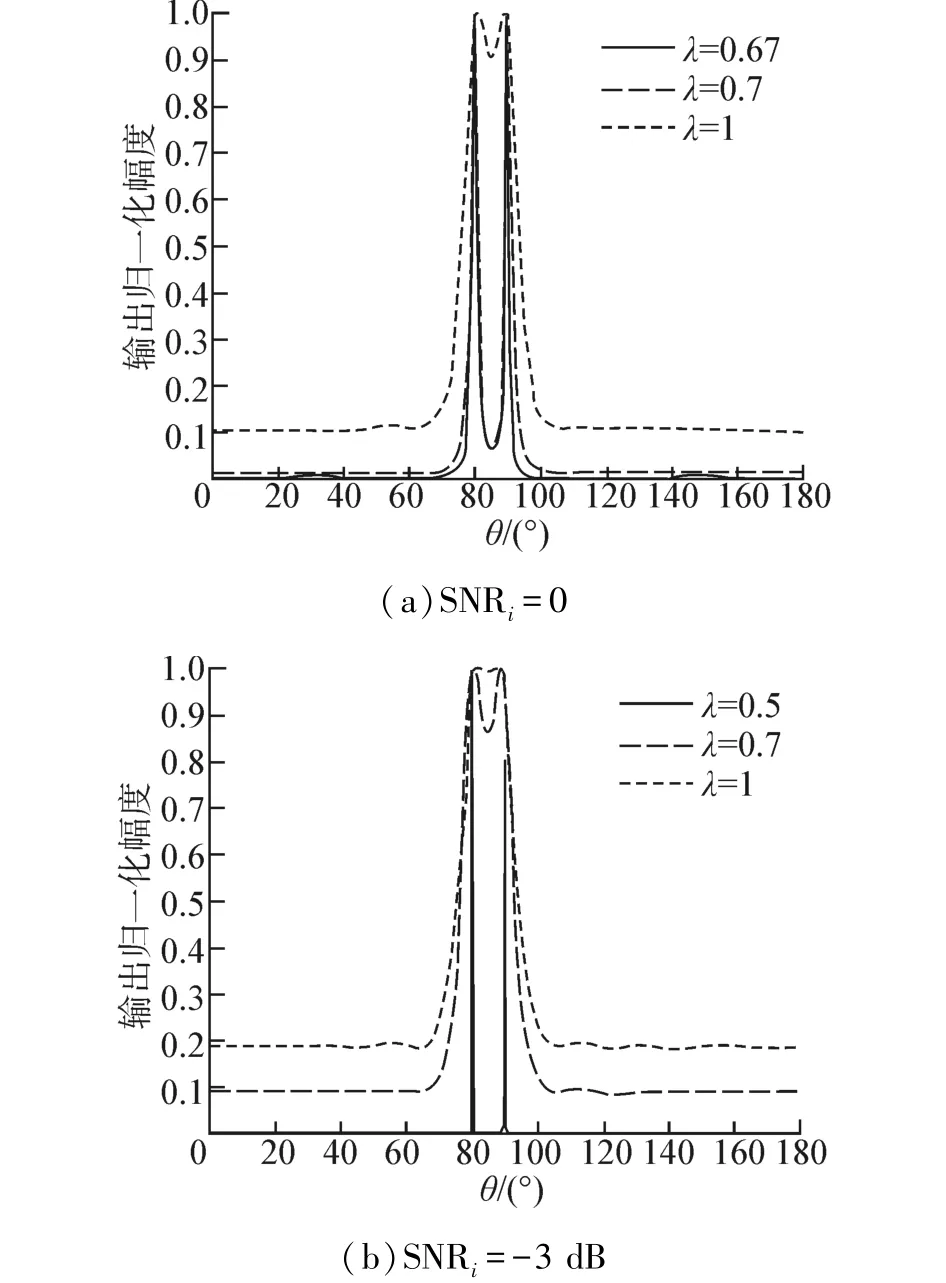
图5 不同信噪比不同减载系数下MVDR波束输出Fig.5 MVDR Beam outputs with different SNR and different reduction coefficients

对多目标时的分辨能力仿真，将目标方位增加40°、60°2个方位，保持各目标声源级相同，而且SNRi＝－15 dB，仿真结果如图6，可以看到80°、90° 2个方向通过适当减少噪声分量后能进行清晰分辨。

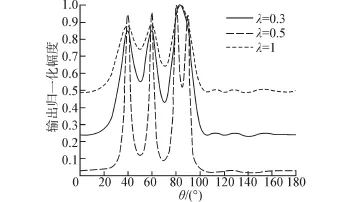
图6 不同减载系数下的MVDR多目标分辨Fig.6 MVDR multitarget distinction with different reduction coefficients

4 结束语

通过理论推导和算法仿真验证可以得出，通过较长时间的估计，在得到稳定的协方差矩阵后，通过对协方差矩阵进行适当的对角减载，能提高CBF和MVDR波束形成器的阵列增益。对于多目标干扰或进行多目标分辨时，MVDR对角减载的基本思路是尽可能减少协方差矩阵对角线上的背景噪声分量。仿真结果证明低输入信噪比时，基于对角减载技术的MVDR波束形成器有效提高了对多目标的分辨能力。

［1］HARRY L，VAN T.Optimum array processing［M］.4nd ed.New York：John-wiley and Sons，2002：48，710.

［2］BIENVENU G，KOPP L.Adaptivity to background noise spatial coherence for high resolution passive methods［C］／／Proc ICASSP.Denver，1980：307-310..

［3］VINOD V R，BOON P N，ANDY W H K.Insights into MUSICLike algorithm［J］.IEEE Transactions on Signal Processing，2013，61（10）：2551-2556.

［4］ROY R，KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques［J］.IEEE Trans ASSP，1989，37（7）：984-995.

［5］XU B Q，SUN L L，XU L，et al.Improvement of the Hilbert method via ESPRIT for detecting rotor fault in induction motors at low slip［J］.IEEE Transactions on Energy Conversion，2013，28（1）：225-233.

［6］陈阳.水声阵列信号处理理论及实验研究［D］.哈尔滨：哈尔滨工程大学，2010：35-38.CHEN Yang.Theoretical and experimental study on underwater acoustic array processing［D］.Harbin：Harbin Engineering University，2010：35-38.

［7］WU F Y，ZHOU Y H，TONG F，et al.Simplified p-norm-like constraint LMS algorithm for efficient estimation of underwater acoustic channels［J］.Journal of Marine Science and Application，2013，11（2）：228-234.

［8］陈欢，何良，杨德森，等.基于幅度补偿的MVDR水下噪声源近场定位识别方法研究［J］.振动与冲击，2012，31（2）：51-54.CHEN Huan，HE Liang，YANG Desen，et al.Underwater noise sources identification in near-field locating based on MVDR method with amplitude compensation［J］.Journal of Vibration and Shock，2012，31（2）：51-54.

［9］吴亚军.MVDR波束形成在噪声源识别中的应用［J］.鱼雷技术，2011，19（2）：101-103.WU Yajun.Application of MVDR beamforming to noise source identification［J］.Torpedo Technology，2011，19（2）：101-103.

［10］罗方方，生雪莉，梅继丹，等.基于MVDR高分辨算法的时反定位技术研究［J］.哈尔滨工程大学学报，2010，31（7）：945-950.LUO Fangfang，SHENG Xueli，MEI Jidan，et al.Time reversal mirror localization technology based on a high-resolution MVDR algorithm［J］.Journal of Harbin Engineering University，2010，31（7）：945-950.

［11］朱永建，徐鹏飞.水声通信网的研究进展及其应用［J］.通信技术，2012，45（6）：36-38.ZHU Yongjian，XU Pengfei.Development and applications of underwater acoustic communication networks［J］.Communications Technology，2012，45（6）：36-38.

［12］QIAO Gang，WANG Wei，GUO Ran，et al.Frequency diversity for OFDM mobile communication via underwater acoustic channels［J］.Journal of Marine Science and Application，2012，11（1）：126-133.

The technique of diagonal reduction processed with underwater acoustic array signal

ZHAO Anbang，ZHOU Bin，SONG Xuejing，BI Xuejie
（Science and Technology on Underwater Acoustic Laboratory，Harbin Engineering University，Harbin 150001，China）

A beamforming method based on array signal covariance matrix diagonal reduction is proposed.By estimating enough snapshots，a stable covariance matrix of the

signal is obtained.Through the appropriate covariance matrix diagonal reduction，the array output gain and the multi-target resolving ability can be improved.In this paper，the conventional beamforming（CBF）and minimum variance distortionless response（MVDR）beamformer＇s array gains were deduced and simulated based on diagonal reduction.The relationship between the array gain and reduction coefficient is analyzed and the reduction coefficient range for resolving multiple targets is studied.The results showed that the diagonal reduction method can improve the multi-target resolving ability of MVDR effectively.

diagonal reduction；multi-target resolving；array gain；minimum variance distortionless response（MVDR）；conventional beamforming（CBF）；array signal

10.3969／j.issn.1006-7043.201311054

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201311054.html

U666.7

A

1006-7043（2014）11-1327-05

2013-11-18.网络出版时间：2014-09-22.

海洋公益性行业科研专项经费资助项目（gz201005001）；国家自然科学基金青年基金资助项目（51009041）；国家自然科学基金资助项目（11374072，61371171）.

赵安邦（1978-），男，教授，博士生导师.

赵安邦，E-mail：zhaoanbang＠hrbeu.edu.cn.