多元线性回归的MATLAB实现

李艳娇，李瑞敏，陈经伟

（1.沈阳建筑大学 建筑设计研究院，辽宁 沈阳 110015；2.沈阳机床（集团）有限责任公司 设计研究院，辽宁 沈阳 110142）

在社会生活及生产实践中经常会遇到这样一种问题，即我们非常关注一个量的变化，而这个量受到另一个或是多个因素的影响.我们想要了解这些因素是如何影响我们最为关注的这个量的以及这些因素对我们最为关注的这个量的影响权重分别有多大.知道了这些，我们就可以对该量变化所反应的相关问题做出分析和评价，并对其未来发展趋势进行预测和控制.这里就要用到数理统计中一个非常重要而普遍的分析方法，即回归分析法.

MATLAB是一个非常强大的通用数学工具，利用其可以轻而易举地解决各学科领域中的一般性数学问题.下面我们首先简单介绍一下回归分析法，在此基础上结合一具体实例，详细介绍利用MATLAB进行多元线性回归分析的几种方法.

1 回归分析及多元线性回归模型

回归分析是研究一个因变量与另一个或一组自变量间定量关系的一种统计分析方法.只有一个自变量的回归分析叫做一元回归分析，有多个自变量的回归分析叫做多元回归分析.按照自变量及因变量间的关系类型，回归分析又有线性回归及非线性回归.所以就有一元线性回归、多元线性回归、一元非线性回归和多元非线性回归四种基本回归分析类型[1-2].

如果一个因变量y与k个自变量x1,x2,...,xk存在线性相关关系，那么就可以用多元线性回归模型

对其进行描述，其中未知常量a0,a1,...,ak称为回归模型系数.若n次抽样，第i次抽样数据为(yi,x1i,x2i,…,xki)，那么就有

其中 ε0,ε1,...,εn为随机误差项[1-2].回归分析的主要任务就是以误差ε0,ε1,...,εn的平方和最小为原则，求取多元线性回归模型的回归系数a0,a1,...,ak.

某单位生产部门有一具体问题，生产人员已明确他们关心的变量y与两个因素x1,x2具有线性相关关系，根据式（1）知可以用二元线性回归模型对其进行描述.车间给出的n=16个测试数据见表1.

现在需要技术部门帮助定量地确定两个因素x1,x2对他们关心的变量y的影响权重并对变量y的变化趋势作出预判以便控制.

2 基于回归算法的MATLAB编程实现

根据式（2）及表1中的16个测试数据有

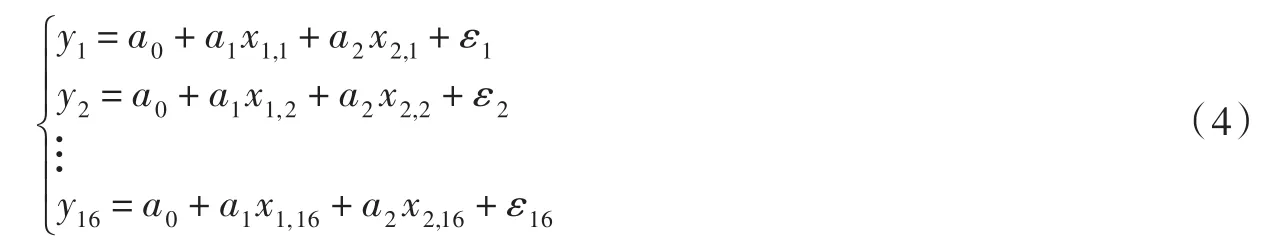
上式可以写成形式

其中：

式（5）是适定方程组，在MATLAB中用 A=inv(X)*Y即可求解，其中inv(X)是X的逆阵.也可以用左除函数“”求解，即A=XY或 A=mldiv ide(X,Y).对于适定方程组来说，XY与inv(X)*Y具有相同的意义[3-4].

基于回归算法求解上述问题的MATLAB程序如下：

x1=[0，0，0，0，0.1，0.1，0.1，0.1，0.2，0.2，0.2，0.2，0.3，0.3，0.3，0.3]；

x2=[0，0.1，0.2，0.3，0，0.1，0.2，0.3，0，0.1，0.2，0.3，0，0.1，0.2，0.3]；

y=[0，2*10^-6，10^-6，-2*10^-6，10^-6，2*10^-6，4*10^-6，-10^-6，-2*10^-6，-10^-6，0，3*10^-6，4*10^-6，-4*10^-6，2*10^-6，5*10^-6]；

X（3，3）=0；Y（3，1）=0；

for i=1：16

X（1，1）=X（1，1）+1；

X（1，2）=X（1，2）+x1（i）；

X（1，3）=X（1，3）+x2（i）；

X（2，1）=X（2，1）+x1（i）；

X（2，2）=X（2，2）+x1（i）^2；

X（2，3）=X（2，3）+x1（i）*x2（i）；

X（3，1）=X（3，1）+x2（i）；

X（3，2）=X（3，2）+x1（i）*x2（i）；

X（3，3）=X（3，3）+x2（i）^2；

Y（1，1）=Y（1，1）+y（i）；

Y（2，1）=Y（2，1）+x1（i）*y（i）；

Y（3，1）=Y（3，1）+x2（i）*y（i）；

end

A=inv（X）*Y%同A=XY

解得结果为a0=-1.0×10-7,a1=3×10-6,a2=3.5×10-6.

3 利用MATLAB预定义函数实现

式（4）可以写成形式

其中：

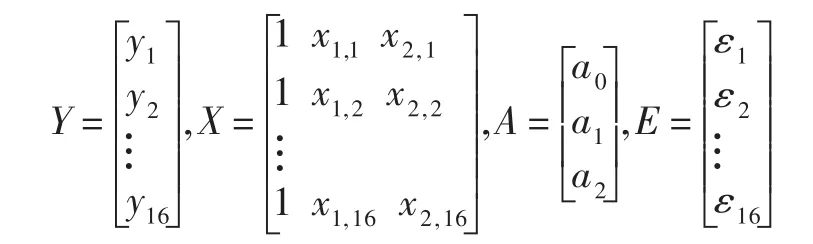
式（6）是一个超定方程组，可以用 A=regress(Y,X)来求解.在MATLAB中，regress函数返回的是Y=XA的最小二乘拟合解[5-6].式（6）方程组也可以用左除函数“”来求解，即 A=XY或 A=mldiv ide(X,Y).对于超定方程组来说，左除函数“”与regress函数相同，返回的也是方程Y=XA的最小二乘拟合解.

利用预定义函数regress求解上述问题的MATLAB程序如下：

x1=[0，0，0，0，0.1，0.1，0.1，0.1，0.2，0.2，0.2，0.2，0.3，0.3，0.3，0.3]'；

x2=[0，0.1，0.2，0.3，0，0.1，0.2，0.3，0，0.1，0.2，0.3，0，0.1，0.2，0.3]'；

Y=[0，2*10^-6，10^-6，-2*10^-6，10^-6，2*10^-6，4*10^-6，-10^-6，-2*10^-6，-10^-6，0，3*10^-6，4*10^-6，-4*10^-6，2*10^-6，5*10^-6]'；

X=[ones（16，1），x1，x2]；

A=regress（Y，X）%同A=XY

解得结果为a0=-1.0×10-7,a1=3×10-6,a2=3.5×10-6.

与上节基于回归算法编程所解得的结果相同.将其代入式（3）知生产人员关心的变量y与两个因素x1,x2之间的关系为y=-1.0×10-7+3×10-6x1+3.5×10-6x2.

4 结束语

（1）多元线性回归问题中一般会有大量数据，它的解算涉及到数理统计、线性代数、矩阵分析及微积分等诸多高等数学知识.MATLAB作为一个强大的通用数学工具，可以在没有专用软件的情况下，快速方便地解决诸如多元线性回归等一般性数学问题.

（2）在MATLAB中，有利用预定义函数及自行编程实现算法两种解决数学问题的基本方法.其中利用预定义函数更为简单快捷，不需要了解具体算法，但不一定所有问题都可以找到最适合的预定义函数；自行编写M文件需要理解原理、熟悉算法，较复杂，但可能更灵活，更适合具体问题的解决.所以实际应用中应采用二者相结合的方法以快速有效地解决问题.

[1]Chatterjee S，Hadi A S，Price B.例解回归分析[M].3版.郑明，徐勤丰，胡瑾瑾，译.北京：中国统计出版社，2004：41-43.

[2]王松桂，陈敏，陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社，2004：28-33.

[3]陈杰.MATLAB宝典[M].3版.北京：电子工业出版社，2007：82-83.

[4]Recktenwald G.数值方法和MATLAB实现与应用[M].伍卫国，万群，张辉，等，译.北京：机械工业出版社，2004：318-320.

[5]Chatterjee S,Hadi A S.Influential Observations,High Leverage Points,and Outliers in Linear Regression[J].Statistical Science,1986,1(3):379-416.

[6]许以超.线性代数与矩阵论[M].2版.北京：高等教育出版社，2008：116-120.