某型多管火箭炮射击精度对重复毁伤影响

宋谢恩，宋卫东，赵成旺，2，佟德飞

（1.军械工程学院，石家庄 050003；2.南京炮兵学院廊坊校区，河北 廊坊 065000）

某型多管火箭炮射击精度对重复毁伤影响

宋谢恩1，宋卫东1，赵成旺1，2，佟德飞1

（1.军械工程学院，石家庄 050003；2.南京炮兵学院廊坊校区，河北 廊坊 065000）

基于射击学理论和毁伤理论，采用矩阵法，建立了某型多管火箭炮射击的重复毁伤分析模型，研究了该型多管火箭炮射击误差对重复毁伤的影响，得出了射击诸元误差和射击散布误差变化对重复毁伤影响的具体规律和二者之间的不同。研究结论对于弹道修正火箭弹设计精度指标确定、弹药消耗规律研究及作战指挥决策具有参考意义。

多管火箭炮，重复毁伤，诸元误差，散布误差

引言

多管火箭炮覆盖面积大，可以同时射击多个目标点，适宜作面杀伤武器，其在战役或战术行动中主要担负歼灭或压制集结的敌有生力量和技术兵器的任务［1］。随着现代战争向信息化智能化发展，我军对普通火箭弹进行了弹道修正，减小了射击误差，提高了射击精度。

重复毁伤是面杀伤武器射击及作战效能评估中必须面对的问题，对于易损目标来说，一次覆盖即为有效毁伤，两次以上的毁伤（毁伤重叠）即为重复毁伤。若集群目标为需要两次覆盖才能毁伤的硬目标，则一次覆盖为无效覆盖，两次覆盖为有效毁伤，两次有效毁伤以上的有效毁伤为重复毁伤，以此类推［2］。本文的射击目标为集群有生力量，属于易损目标，重复毁伤应计算两次及以上毁伤。

火箭弹精度的提高，势必对重复毁伤造成影响，而重复毁伤程度的度量对于研究混合类目标的毁伤效率、目标分配优化等是非常重要的。

1 火箭炮重复毁伤分析模型

面杀伤弹药的重复毁伤问题，目前为止还没有公认的数学模型，也无法通过大模型射击进行试验并通过统计方法进行研究。本文借鉴文献［3］中提出的矩阵法及文献［4］中提出的像素法，对多管火箭炮重复毁伤与射击精度的关系进行建模分析，以期得到二者之间的关系。

像素点法的基本思想为：在图形状态下，将对应于炸点的毁伤区域用特定的颜色进行填充，经过射击后，目标区域上便形象地显示出对目标的毁伤情况。统计特定颜色的像素点数占总像素点数的比例，即为该次射击的毁伤程度，但由于其涉及计算机图形学，虽然直观，但实现起来有一定难度。矩阵法的基本思想为：将目标幅员平均划分为若干网格，建立与网格对应的矩阵，即矩阵的元素与目标幅员各个小格一一对应。各网格为最小单位（如1 m2），不可再分。以矩阵元素的值来表示毁伤次数，0为没有毁伤，1为1次毁伤，n为n次毁伤。先将矩阵元素值初始化为0。射击结束后，对矩阵元素的数值进行统计分析，得出重复毁伤情况。

1.1 重复毁伤概念

本文对于重复毁伤的研究以重复毁伤率作为指标，重复毁伤率具体可分为两种：

重复毁伤率Ⅰ，是指目标区域中被多余覆盖过的面积的累加（多覆盖一次累加一次）与总目标幅员比值，在数值上等于落入射击区域的火箭弹无重叠覆盖目标幅员所达到的毁伤与实际毁伤之间的差值。其在物理意义上更偏重于我方火力无效投入，即过于毁伤需要的火力投入。

重复毁伤率Ⅱ，是指目标区域中多余覆盖的区域（不论覆盖几次，均只计算一次）所占目标幅员的比例。在物理意义上更偏重于敌方受到重复毁伤的情况，即目标幅员中被重复毁伤区域所占比例。

1.2 射击误差计算

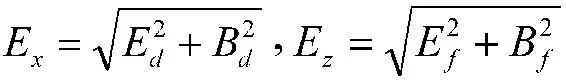
1.3 炸点位置确定与毁伤判定

设（μx，μz）为瞄准点坐标。本模型根据现有火箭炮营装备配置情况，行3标尺6方向分划射击；射击的距离差和射向间隔由最有利火力分配方法确定，具体计算如下［6］：

式中，k、n为射击时表尺数和方向分划数，Ed、Ef分别为诸元误差的距离、方向中间误差，Bd、Bf分别为散布误差的距离、方向中间误差，γ2为对二维目标实施最有利火力分配时的一个计算系数，N为射弹量，v为目标幅员面积，τ为补偿系数，在目标幅员较小时，其值为1，通常情况为简便计算，均取为1，ω为有效毁伤单元目标所需直接命中弹数，ρ为炮兵常数0.476 94。

u1，u2是两个服从标准正态分布的随机数，即u1，u2～N（0，1），可由计算机程序随机生成。

这样通过两个服从标准正态分布的随机数，射击误差的均方差和瞄准点坐标可以模拟一发弹的炸点，获取坐标。以炸点为圆心，以毁伤半径为半径的圆覆盖的网格被毁伤，将与其对应的矩阵元素值加1。

重复毁伤率Ⅰ等于重复毁伤处对应的元素值减1再求和，所得和与总元素数量之比，该指标反映无效毁伤在数量上的统计；重复毁伤率Ⅱ等于矩阵元素值大于1的网格数量占总网格数的比例，该指标反映被重复毁伤的有生力量占总体数量的比例。求出不同射击误差对应的重复毁伤率Ⅰ、Ⅱ，采用拟合插值得出重复毁伤率变化曲线。

1.4 模型初值设置

将目标幅员网格对应的矩阵初始化为零矩阵。以某火箭炮营对集群目标有生力量进行射击为研究对象，目标集结地距发射阵地20 000 m，火箭炮营下辖3个连，每连6辆自行火箭炮车，每车一次齐射40枚火箭弹，目标幅员700 m×700 m，营诸元误差Ed=74 m、Ef=26 m，散布误差Bd=106 m、Bf=58 m，毁伤幅员分别为100 m2、200 m2、300 m2、400 m2。

在研究诸元误差对重复毁伤的影响时，诸元误差初始值为Ed0=111 m、Ef0=39 m（1.5倍的射表原始诸元误差，即74×1.5=111、26×1.5=39），以0.99的幅度衰减，衰减100次（0.99100=0.366），最终Ed=40.6 m、Ef=14.3 m（约0.5倍的射表原始诸元误差，即74×0.549=40.6、26×0.549=14.3）。

在研究散布误差对重复毁伤的影响时，散布误差初始值为Bd0=159 m、Bf0=87 m（1.5倍的射表原始散布误差，即106×1.5=159、58×1.5=87），以0.99的幅度衰减，衰减100次（0.99100=0.366），最终Bd=57.9 m、Bf=31.6 m（约0.5倍的射表原始散布误差，即106×0.549=58.2、58×0.549=31.8）。

表1 初值设置

2 诸元误差对重复毁伤影响

重复毁伤率Ⅰ、Ⅱ随诸元误差变化基本一致，只是具体数值不同，详细如表2，图1所示。

表2中横向对比得出，当诸元误差一定时随着毁伤幅员的增大，重复毁伤率Ⅰ、Ⅱ也随之增大。

纵向对比可得出，毁伤幅员S一定时，重复毁伤率Ⅰ随着诸元误差的减小而增大，即射击准确度越高重复毁伤率Ⅰ越大。当射击距离误差Ed（方向误差Ef）从159 m（87 m）降低至58 m（33 m）时：

S=100 m2，重复毁伤率Ⅰ从 1.22%增大到1.94%，增大了59.0%；重复毁伤率Ⅱ从1.11%增大到1.69%，增大了52.3%；

S=200 m2，重复毁伤率Ⅰ从 3.96%增大到5.93%，增大了49.8%；重复毁伤率Ⅱ从3.35%增大到4.73%，增大了41.2%；

S=300 m2，重复毁伤率Ⅰ从 7.72%增大到11.38%，增大了47.4%；重复毁伤率Ⅱ从6.19%增大到8.47%，增大了36.8%；

S=400 m2，重复毁伤率Ⅰ从12.45%增大到18.52%，增大了48.8%；重复毁伤率Ⅱ从9.47%增大到12.85%，增大了35.7%。

毁伤幅员越大，重复毁伤率Ⅰ、Ⅱ增大的幅度越小，但当毁伤幅员增大到一定值时，这种幅度变化趋于消失。

由于不同毁伤幅员曲线类似，在此抽取毁伤幅员S=200 m2为例进行详细分析。根据数据特点，对重复毁伤率Ⅰ、Ⅱ随诸元误差变化曲线采用3次多项式拟合，并求一阶导数，如图1所示。

表2 不同诸元误差对应的重复毁伤率Ⅰ、Ⅱ

图1 重复毁伤率Ⅰ、Ⅱ随诸元误差变化曲线及其导数（S=200）

由表1、图1（a）可知，当其他射击条件一定时，重复毁伤率Ⅰ、Ⅱ随着射击诸元误差的减小而增大，其变化曲线是凸曲线，且二者形状很接近。由图表均可得出，重复毁伤率Ⅰ的值高于Ⅱ，由二者定义可知，其差值反映了毁伤次数高于两次的重复毁伤情况，且差值越大，高于两次的重复毁伤所占比例越大。由图1（a）可以明显看出，Ed、Ef越小，差值越大，说明高于两次的重复毁伤所占比例随着Ed、Ef减小而增大。

由图1（b）可知变化曲线的斜率是单调递减的，即重复毁伤率Ⅰ、Ⅱ随着射击诸元误差减小而增大的幅度越来越小。由此可知，当诸元误差较大时，其变化对重复毁伤情况影响较大；反之则较小。重复毁伤率Ⅱ的斜率值明显小于重复毁伤率Ⅰ，说明Ⅱ整体变化幅度小于Ⅰ，这与实际情况是相符的。

3 散布误差对重复毁伤影响

重复毁伤率Ⅰ、Ⅱ随散布误差变化略有不同，详细如图2、图3，表3、表4所示（表3中增幅的计算与2.2中相同）。

图2 重复毁伤率Ⅰ、Ⅱ随散布误差变化曲线及其导数（S=100）

图3 重复毁伤率Ⅰ、Ⅱ随散布误差变化曲线及其导数（S=300）

由表3横向对比可以得出，当散布误差一定时随着毁伤幅员的增大，重复毁伤率Ⅰ、Ⅱ也随之增大。

纵向对比可以得出，毁伤幅员S一定时，重复毁伤率Ⅰ随着散布误差的减小而增大，即射击密集度越高重复毁伤率Ⅰ越大，且毁伤幅员越大，重复毁伤率Ⅰ、Ⅱ增大的幅度越小。但当散布误差减小到一定值时，重复毁伤率基本不再变化。对于本文所设变化范围，整体而言散布误差变化对重复毁伤的影响大于诸元误差。但散布误差较小时，其变化对重复毁伤的影响远小于诸元误差。

分析不同毁伤幅员数据特点可知，100、200类似，300、400类似，故取S=100、300为例，对重复毁伤率Ⅰ、Ⅱ随散布误差变化曲线采用13次多项式拟合，并求一阶和二阶导数，如图2、图3所示。图2（a）中重复毁伤率Ⅰ、Ⅱ曲线均出现两个斜率突变点，整体曲线近似于3条斜率不同的直线拼接而成；图2（b）为一阶导数，显示了重复毁伤率Ⅰ、Ⅱ各自的 3种不同斜率（10-4），Ⅰ：2.1，1.2，0，Ⅱ：1.8，0.9，0，斜率均递减；图2（c）为二阶导数，其20～30、70～80之间的极值点就是斜率突变点，经求解，重复毁伤率Ⅰ、Ⅱ极值点相同，均为g=26、76（Bd=122、74，Bf=67、41）。

图3与图2意义相同，只是图3中仅出现了一个斜率突变点，g=47，斜率（10-4）Ⅰ：2.1，1.2，0，Ⅱ：1.8，0.9，0。

统计不同毁伤幅员对应的重复毁伤率Ⅰ、Ⅱ随散布误差变化曲线数据特点，得182页表4。可以明显看出，毁伤幅员越大，斜率越大，斜率突变点的位置越靠后，突变点对应的散布误差越小。但当散布误差减小到一定值后，斜率变为0，即散布误差变化对重复毁伤不再产生影响。

4 结束语

本文基于射击理论和毁伤理论，以某型火箭炮

表3 不同散布误差对应的重复毁伤率Ⅰ、Ⅱ

营对集群有生力量射击为研究对象，综合矩阵法和像素点法，建立了重复毁伤的分析模型，通过对计算结果的分析，研究了射击精度变化对重复毁伤的影响，得出了以下结论：

表4 重复毁伤率Ⅰ、Ⅱ随散布误差变化曲线数据统计

①随着射击误差的减小，重复毁伤增加，且高次数重复毁伤所占比例增加；

②在射击误差较大的情况下，射击诸元误差对重复毁伤的影响小于散布误差；反之，则大于散布误差；

③射击诸元误差在减小到一定值后，对重复毁伤情况影响基本消失。

研究成果对于火箭炮武器系统采用弹道修正弹后的毁伤效能评估及射击指挥具有参考意义，对于面杀伤武器系统重复毁伤规律的研究，是有益的探索。

［1］李新龙.多管火箭武器系统及其效能［M］.北京：国防工业出版社，2008.

［2］杨伯忠，陈运生.地炮发射子母弹子弹重叠问题研究［J］.弹道学报，1999，11（2）：67-70.

［3］杨小林，王震宇.矩阵仿真法与战斗部威力评估［J］.火力与指挥控制，2010，35（3）：86-88.

［4］陈立新.压制火炮作战能力指数研究及应用［D］.合肥：合肥炮兵学院，1995.

［5］张平乐.炮兵射击误差理论［M］.北京：解放军出版社，2004.

［6］江 华.炮兵射击基本理论分析［M］.北京：兵器工业出版社，2004.

Research on Influence of Firing Error on Repetitious Damage for Certain Multiple Rocket

SONG Xie-en1，SONG Wei-dong1，ZHAO Cheng-wang1，2，TONG De-fei1
（1.Ordnance Engineering College，Shijiazhuang 050003，China；
2.Langfang Campus of Nanjing Artillery Academy，Langfang 065000，China）

A repetitious damage analysis model is proposed with matrix-simulation method based on firing and destroys theory of artillery，and the influence of firing error on repetitious damage is studied.The influence of firing error and dispersion error on repetitious damage is analyzed through simulation result，and also the different impaction on the law of repetitious damage.Research conclusions have reference value for the determination of trajectory correction rocket design accuracy index，research of ammunition consumption law and operational command decisions.

multiple rocket，repetitious damage，data error，dispersion error

TJ393

A

1002-0640（20144）1111--0175-04

2013-08-15

2013-10-31

宋谢恩（1988- ），男，河北定州人，在读硕士研究生。研究方向：弹道学理论与应用。