导弹自动驾驶仪改进遗传模糊控制器设计*
2014-06-15潘琢金郭效哲毛艳娥
潘琢金,郭效哲,毛艳娥,杨 华
(沈阳航空航天大学计算机学院,沈阳 110136)
导弹自动驾驶仪改进遗传模糊控制器设计*
潘琢金,郭效哲,毛艳娥,杨 华
(沈阳航空航天大学计算机学院,沈阳 110136)
针对导弹飞行控制系统具有参考模型不精确,非线性时变的特点,设计了一种新型的导弹自动驾驶仪的模拟退火遗传模糊PID控制器。该控制器是利用模糊控制器的模糊推理能力,在线整定PID控制器参数,再采用遗传算法与模拟退火算法结合,离线搜索寻优模糊控制器中的隶属函数参数集。Matlab仿真实验结果表明,所设计的控制器能够使系统具有良好的动态性能、鲁棒性以及全弹道性能,利用模糊查询表可满足系统的实时性要求,工程应用前景较好。
导弹自动驾驶仪,模拟退火,遗传算法,模糊控制
引言
导弹自动驾驶仪是导弹飞行控制系统中的稳定系统,其任务是克服导弹飞行过程中所遇到的干扰,实时准确地对导弹姿态运动进行控制和稳定,使导弹自动按照预定轨迹飞行。然而,导弹飞行控制系统模型具有非线性时变的特点,传统的控制方式已不能满足其发展需求,智能控制系统是解决这一复杂对象控制问题的有效手段。本文以导弹俯仰通道为例,选取弹道上某特征点设计控制器。首先将遗传算法(GA)与模拟退火算法(SA)相结合,变为模拟退火遗传算法(GASA),然后用GASA离线寻优模糊PID控制器(FC-PID)中的隶属函数参数集,设计出模拟退火遗传模糊 PID控制器(GASAFC-PID)。
1 导弹俯仰通道数学模型
本文采用系数冻结法描述弹体角运动,即忽略导弹速度变化等次要因素,只考虑导弹的姿态变化,对其纵向短周期运动方程进行拉式变换,在运动参数偏量初始值为零的前提下,可得弹体纵向传递函数[1]:
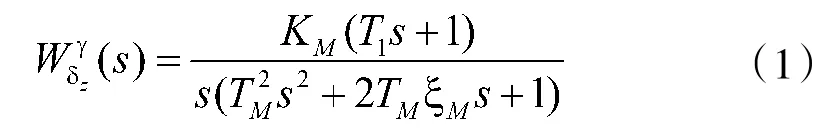
其中,KM为导弹纵向传递系数,T1为气动力时间常数,TM为纵向时间常数,ξM为相对阻尼系数。已知某弹道特征点各参数分别为:KM=0.940,T1=1.697,TM=0.206,ξM=0.097,则该特征点弹体纵向传递函数可写成如下形式:
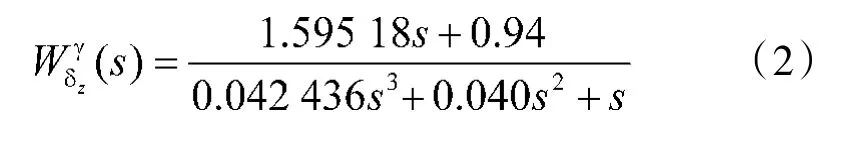
2 模糊PID控制器设计(FC-PID)
模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数字控制。PID控制是比例积分微分控制,目前已被广泛应用。
模糊PID控制是将模糊推理和PID控制结合,找出PID 3个参数Kp、Ki、Kd与e和ec(误差变化率)之间的模糊关系,在运行中不断检测e和ec,根据模糊控制规则对3个参数在线修改,以满足不同的e和ec对控制参数的不同要求,而使被控对象有良好的动、静态性能。模糊PID控制器原理图,如图1所示。
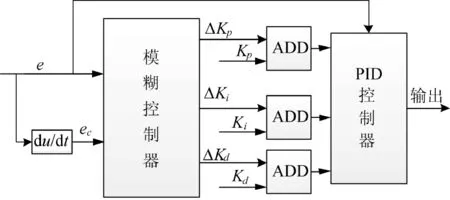
图1 模糊PID原理图
模糊PID控制器的输入变量为:e和ec,对应的语言变量分别为E、EC;输出变量为:ΔKp、ΔKi、ΔKd,对应的模糊语言变量分别为KP、KI、KD;将5个输入输出变量的模糊集均设为{NB,NM,NS,Z,PS,PM,PB};模糊论域均设为[-3,3];e的量化因子设为3,ec的量化因子设为0.5,ΔKp,ΔKi,ΔKd的比例因子分别设为1.66,1.66,0.33;选择输入输出变量的各语言变量隶属度函数都为均匀三角形。控制器的模糊控制规则如表1所示。
去模糊化采用重心法,PID控制器的初值设为:Kp=5,Ki=5,Kd=1.8。下文所介绍的控制器,均在该模糊PID控制器基础上改进完成。
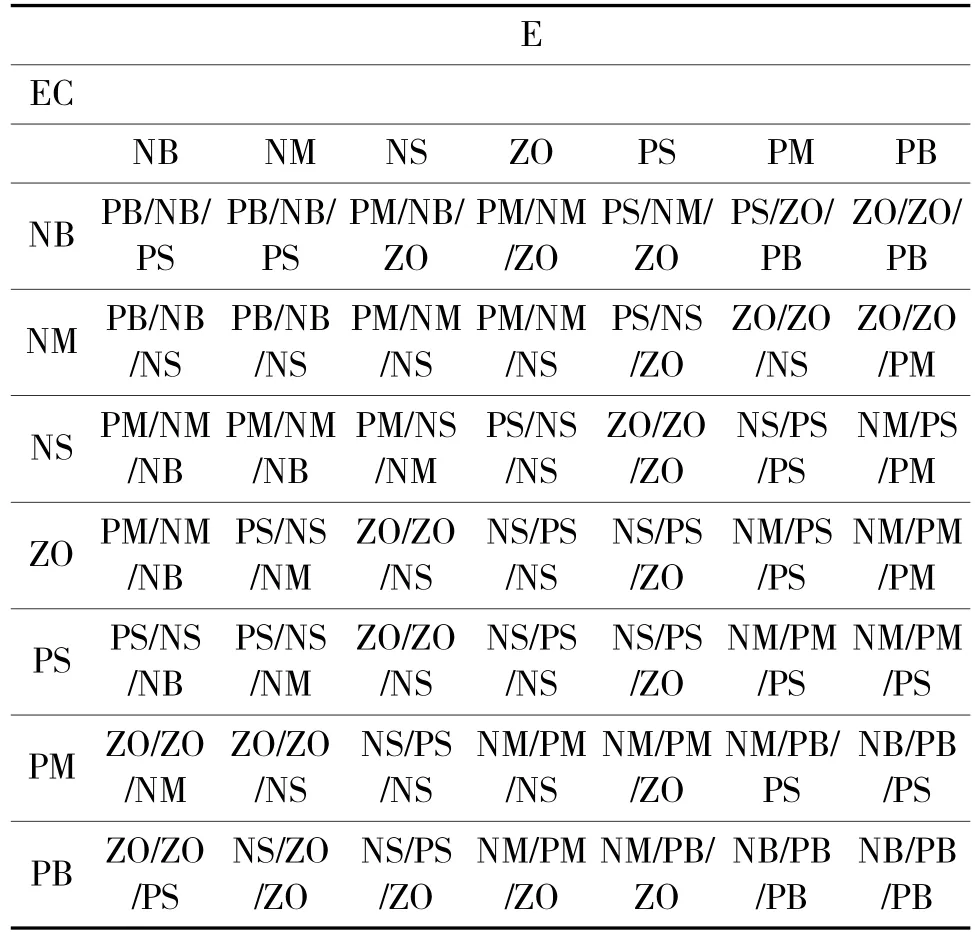
表1 模糊控制规则KP/KI/KD
3 遗传模糊PID控制器设计(GAFC-PID)
遗传算法是基于自然选择和基因遗传学原理的随机搜索算法。它使用选择、交叉和变异等基因操作,在串结构之间进行有组织但又随机的信息交换,优胜劣汰,从而逐渐逼近最优解。遗传模糊控制是利用遗传算法的特性,对模糊控制器的隶属函数、模糊规则、量化因子进行离线或在线优化。由于遗传算法的计算量较大,目前对模糊控制器在线优化意义不大,因此,本文采用离线优化模糊控制器中的隶属度函数。

图2 遗传算法优化模糊PID控制器

图3 待寻优参数的物理意义
遗传算法离线优化模糊PID控制器的步骤是:
(1)随机产生一个种群,种群规模为100;
(2)按序用每个染色体更新模糊控制器(FC)的隶属函数参数,参数的物理意义如上页图3所示。将所有FC依次更新入控制系统,引入阶跃信号运行系统,依照适应度函数计算出每个染色体的适应度值;
(3)按适应度高低进行遗传操作:选择、交叉、变异,生成子代种群;
(4)重复(2),(3)步骤,直至找到优化解,具体流程见图4所示。
3.1 隶属函数编码
前述的模糊PID控制器有E、EC、KP、KI和KD 5个输入输出变量,每个变量都拥有NB等7个语言变量。选取图3中的待定参数{a1,a2,a3,a4…a60}为待寻优参数集,以此作为遗传算法的编码串,编码方式采用实值编码。每个输入输出变量有12个待寻优参数,因此,5个变量共有60个参数,即编码串长度为60。
3.2 适应度函数的确定
适应度函数是遗传算法的关键环节,它反映出个体对于结果的好坏程度。适应度越高,表明个体更接近最优解。在本系统中,寻优的目标是阶跃响应时,快速的上升时间,较小的超调量和稳态误差。在此,构造以下目标函数:

式中,u为系统输出,u*为期望输出,λ1,λ2,λ3为常数,假设系统反馈通道的传递函数为1,则目标函数可以简化为以下形式:
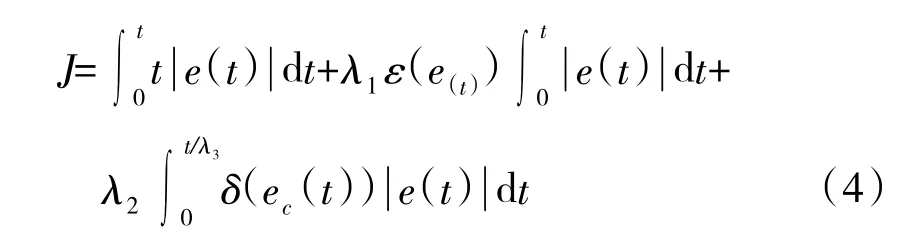
式(4)中,第一项为时间乘以误差绝对值积分(ITAE)性能指标;第二项和第三项为罚函数项,第二项的引入是为了抑制系统响应过程中的超调以及稳态误差;第三项的引入是为了防止系统在响应初期,由于PID控制器Kp过大而Kd过小导致的振颤现象,当振颤现象发生时,罚函数可判别响应曲线斜率为0的位置,也就是振荡的极点,并依极值的绝对值大小进行正比惩罚。式中取λ1=0.01,λ2= 0.5,λ3=4。系统适应度函数与目标函数的关系为:

3.3 遗传算法选择操作
选择操作采用锦标赛法,对种群择优的步骤:
(1)种群规模为100,随机从种群中选择小于100个染色体,一般选择数量为规模的一半,这里取50;
(2)在这50个染色体中,选择适应度最大的个体,作为子代染色体;
(3)循环步骤(1),步骤(2),直至子代染色体数量达到100。
这里选取选择概率Ps=0.6。
3.4 遗传算法交叉操作
交叉操作采用算术交叉的方法,算术交叉操作与染色体的基因重组在形式上不同,但却体现了父代之间信息交换的特性:
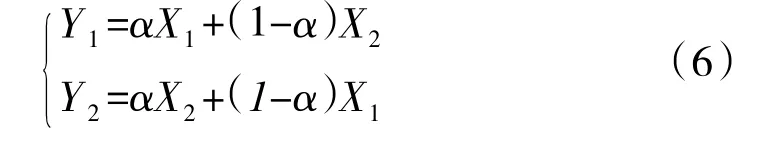
其中,Y1,Y2为子代染色体,X1,X2为父代染色体,α为(0,1)上的随机数。
3.5 遗传算法变异操作
变异操作采用均匀变异。均匀变异操作是指分别用符合某一范围内均匀分布的随机数,以某一较小的概率来替换染色体编码串中各个基因座上的原有基因值。均匀变异的具体操作过程是:
①指定染色体编码串中某些基因座为变异点;②对每一个变异点,以变异概率Pm从对应基因的取值范围内取一随机数代替原有基因值。
选取变异概率Pm=0.005。
4 模拟退火遗传模糊PID控制器设计
模拟退火算法(SA)的基本思想是:通过模拟高温物体退火过程的方法,找到全局最优或近似全局最优解。其特点是以一定的概率来接受一个比当前解要差的解,因此,有可能会跳出局部的最优解,达到全局的最优解。遗传算法(GA)很容易陷入局部最优解,因此,将SA与GA结合,其寻优能力会有所提高。
本文将SA引入GA中,使SA成为GA的一个退火算子。在优化过程中,某一染色体更新了模糊控制器(FC)的隶属函数,将新的FC换入系统中运行,适应度函数可计算出适应度值f1,对该染色体加入小扰动,即对染色体中每个基因值进行小范围的随机变化,再更新FC,运行系统,计算出此时的适应度值f2,比较f1和f2值的大小,若f1<f2,则接受新的染色体,若f1>f2,则依概率Psa接受新染色体。而后进行遗传算法的选择交叉变异操作。Psa的计算公式为:

其中,k为常数,N为遗传代数。由上式可知,f1,f2的差值越大,Psa越小,即接受新染色体的概率越小。GASAFC-PID控制器的程序流程图,如图4所示。
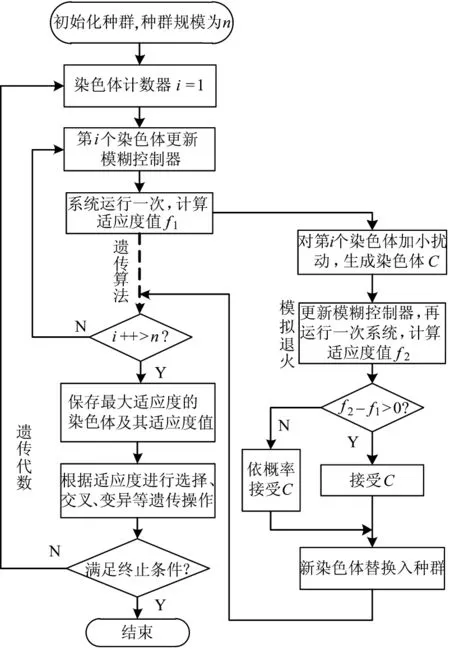
图4 GASAFC-PID程序流程图
5 Matlab仿真
本系统采用Matlab及其工具Simulink对导弹俯仰通道上的某特征点进行GASA仿真寻优。并对各控制器的性能进行了仿真比较。仿真采样时间设为0.01 s,被控对象传递函数为式(2)。
图5为采用GA寻优与采用GASA寻优的适应度比较。结果表明,GASA算法比GA算法具有更快的收敛速度和更优化的解。

图5 GASA与GA寻优比较
图6为GASA,GA寻优后,各控制器的阶跃响应比较。结果表明,PID控制器在初值为Kp=5,Ki=5, Kd=1.8的情况下,上升时间为0.565 s,超调量为13%,稳态误差为0.005,调节时间为5.2 s;普通FC-PID的上升时间为0.457 s,超调量为7.8%,稳态误差为0.001,调节时间为6 s;GAFC-PID的上升时间为0.299 s,超调量为2.35%,稳态误差为0,调节时间为1.6 s;GASAFC-PID的上升时间为0.31 s,超调量为1.6%,稳态误差为0,调节时间为1.6 s。
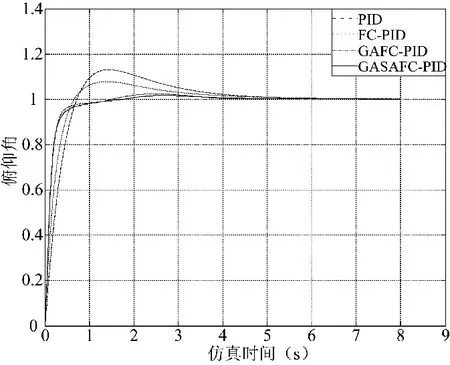
图6 各控制器阶跃响应比较
图7为各控制器在加入1倍的常值干扰后的阶跃响应,结果表明,GAFC-PID的上升时间为0.245 s,超调量为8.1%,稳态误差为0,调节时间为3.5 s;GASAFC-PID的上升时间为0.25 s,超调量为6.6%,稳态误差为0,调节时间为2.9 s。GASAFC-PID比GAFC-PID具有更高的抗干扰性能。
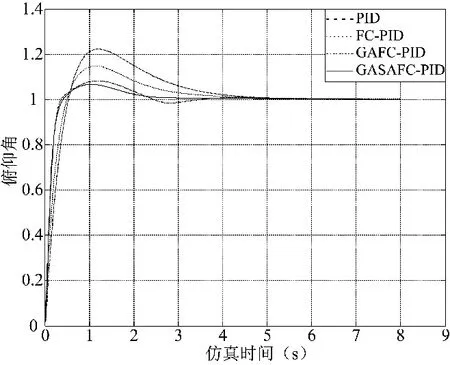
图7 加入1倍常值干扰
图8为GASAFC-PID控制器在全弹道响应的飞行包络,即各特征点的阶跃响应。结果表明,GASAFC-PID鲁棒性强,其整体性能优于其他控制器。

图8 GASAFC-PID飞行包络
6 结 论
模拟退火遗传模糊PID控制器是通过离线优化模糊PID的隶属度函数参数,使模糊控制器具有更好的控制效果,动态性能与鲁棒性均有所提高。优化后的控制器还可以通过模糊查询表,使控制器的实时性显著提高,满足工程应用中,实时计算量严苛的要求。实验证明,该控制器具有较好的应用前景。
[1]可 伟,乔海岩,史 震.基于QFT的导弹姿态稳定回路设计[J].战术导弹控制技术,2009,31(1):29-32.
[2] Sreenuch T,TsourdosA,HughesE Jetal.Fuzzy Gain-Scheduled Missile Autopilot Design Using Evolutionary Algorithms[C]//Portland:American Control Conference,2005:346-351.
[3]Moulay R D,Mohamed C,Ahmed E.Genetic Algorithms Based Fuzzy Speed Controllers for Indirect Field Oriented Control of Induction Motor Drive[J].International Journal of Circuits,Systems and SignalProcessing,2012,6(1):21-28.
[4]Zhou Y S,Lai L Y.Optimal Design for Fuzzy Controllers by Genetic Algorithms[J].IEEE Transactions on Industry Applications,2000,36(1):93-97.
[5]Rahul L N,Ron M N.Use of Genetic Algorithms and Evolutionary Strategies to Develop an Adaptive Fuzzy Logic Controller for a Cooling Coil-Comparison of the AFLC with a Standard PID Controller[J].Energy and Buildings,2012,45(2):169-180.
[6]郑鲲鹏,华建林,姜 殿.三回路驾驶仪控制下的导弹静不稳定性边界[J].四川兵工学报,2013,34(3):32-35.
[7]甘旭升,端木京顺,张小花.导弹自动驾驶仪的模糊自整定免疫PID控制[J].火力与指挥控制,2007,32(6):70-73.
Fuzzy Logic Controllers Using Modified Genetic Algorithms for Missile Autopilot
PAN Zhuo-jin,GUO Xiao-zhe,MAO Yan-e,YANG Hua
(School of Computer Science,Shenyang Aerospace University,Shenyang 110136,China)
The missile flight control system has the characteristics of model inaccuracy,nonlinearity and time-varying.This paper designs a new Fuzzy-PID controller optimized by simulated annealing genetic algorithm for missile autopilot.The new controller is to use ability of the inference of Fuzzy-PID Controller to set the parameters of PID controller,use genetic algorithm and simulated annealing algorithm to optimize the parameters of membership function of Fuzzy-PID Controller.Matlab simulation results show that the controller has good dynamic performance,robustness and good performance of every point on the trajectory.By using fuzzy lookup table,the controller can meet the real-time requirement and has a good engineering application prospect.
missile autopilot,simulated annealing algorithms,genetic algorithms,fuzzy control
TP273+.4
A
1002-0640(2014)11-0137-04
2013-08-25
2013-11-07
2013年辽宁省自然科学联合基金(2013024002);辽宁省科学基金项目(20091059);中国航空科学基金资助项目(2008ZC54)
潘琢金(1962- ),男,吉林通化人,教授,硕士生导师。研究方向:为嵌入式系统、计算机检测与控制。
