电磁催泪风暴系统引信参数分析与仿真

杨风

（武警工程大学，西安 710086）

电磁催泪风暴系统引信参数分析与仿真

杨风

（武警工程大学，西安 710086）

介绍了电磁催泪风暴系统的结构原理，应用数值分析法确定了引信线圈的发火电压标准，结合Maxwell电磁仿真软件建立了两组发射单元模型，分析得到了引信线圈的最佳位置、最优匝数及最小间距。为确定电磁感应式引信参数提供了一种较好方案。

电磁发射，电磁感应，引信，仿真

引言

经过一百多年的发展，电磁发射技术已经取得了巨大的进步，虽然在高射频和高射速领域仍然存在许多难题，但在低速方面已经可以运用到实际的装备研制上来，且与常规的化学发射方式相比，电磁发射方式具有明显的优势。

电磁催泪风暴武器系统是指能够运用电磁发射技术极速发射大量催泪弹药的武器系统。它能通过调节供电电压和弹药的发射角度，实现对弹药的射击距离和方向的控制，既可单发定点射击，也可结合其强大的高射速在短暂时间内形成大面积的催泪烟雾，驱散闹事人群，同时，具有强大的震慑作用。由于其高射速、打击距离和方向可控、噪声和污染低等优点，很好地弥补了武警部队现有装备无法达到快速驱散的装备空缺，适合武警部队处置大规模群体性事件。

1 结构原理

电磁催泪风暴武器系统主要运用单级同步感应线圈发射器技术［1］结合“金属风暴”模型构建的武器系统。系统由16管发射器组成，呈4×4矩阵结构，可拆分成12管、9管等结构。每管发射器包括4组单级感应线圈发射单元，采用多弹串联预装填技术［3］，一次可装填4枚弹，4枚弹药紧靠排列，一枚弹药对应一个发射单元，发射时，4枚弹药按前后顺序依次发射（发射管简要示意图如下页图1所示，第3、4号发射单元与第1、2号相同）。

发射时，弹药1受到驱动线圈1向前的作用力向前运动，而弹药2及后面的弹药受到向后的作用力，由于被顶死，所以不会运动。弹药1在极短的时间内达到要求速度，引信1在此过程中受到强电磁感应，成功发火，后几发弹药的引信由于准确设计，达不到发火电压，安全可靠。

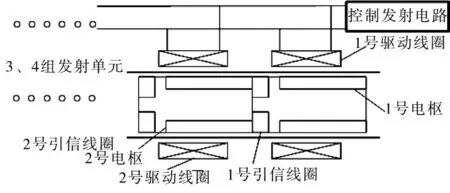
图1 发射管简要示意图

由于成本要求，电磁催泪风暴系统弹药采用简易电磁感应式电火花引信，其结构简图如图2所示。在发射过程中，受到驱动线圈磁场作用，引信感应线圈产生高压，连接在感应线圈的电极击穿空气点燃弹药。那么，引信感应线圈的匝数、位置、直径，以及前一发弹药发射时对后一发弹药引信影响的大小即引信的间距值得深入研究。

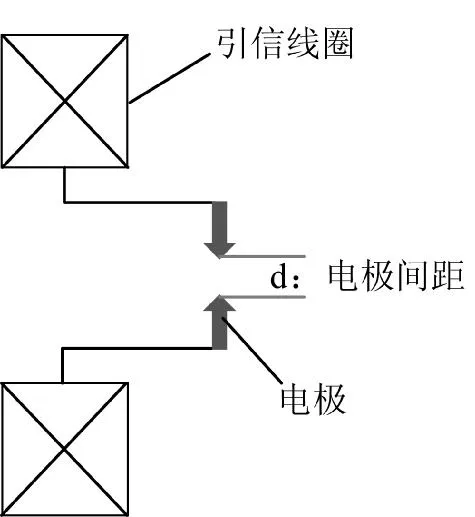
图2 引信结构简图

2 发火电压标准

根据汤姆森击穿理论，当γeαh=1+γ时，电极的击穿电压V满足：

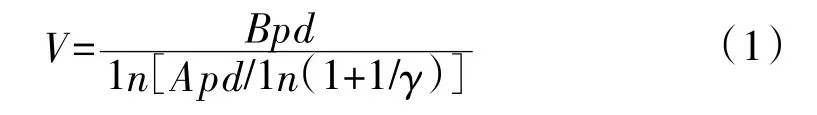
式中：p为电极间的大气电压；d为电极间距；A、B为常数；γ为二次电离系数。

由于在实际中难以得知γ的值，因此，要将式（1）变形，文献［4］通过研究，可将式（1）改写为

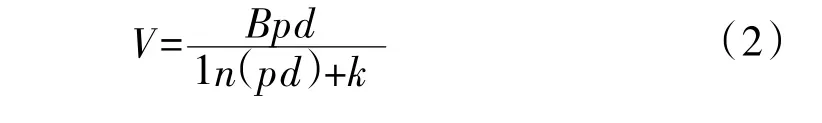
式中，k=1n［A/1n（1+1/γ）］。

文献［5］给出了常数B在空气中的具体值为2 737.5。

文献［6］通过计算得到了k的值如表1。

表1 不同压强·间距下空气的k值

因此，在标准大气压下，电极间距小于2 mm，空气的击穿电压公式可写成：

将电极间距取0.8 mm，则电极击穿电压为2.4 kV。令前一枚引信发火安全系数取1.25，后一发引信不发火安全系数取0.5，那么则要求弹药在发射过程中，前一枚引信峰值电压要超过3 kV，后一枚引信峰值电压要低于1.2 kV。

引信的电压标准已明确。要对引信线圈的感应电压进行求解，就得计算出其与驱动线圈间互感、自感与互感梯度。但困难的是自感、互感与互感梯度的计算涉及三阶椭圆积分的复杂函数［7］，基本不能得到解析解，只能用数值模拟的方法得到动态的完整解。鉴于以上难点问题，本文结合高度集成化的Ansoft Maxwell仿真软件模拟催泪弹发射的动态过程及引信的感应电压。

3 仿真过程及结果分析

3.1 仿真设置

Ansoft Maxwell［8］是基于麦克斯韦微分方程，采用有限元离散形式，将工程中的电磁场计算转变为庞大的矩阵求解。它具有准确、快捷、分布式计算、并行式计算等诸多优点，不仅可以对单个电磁机构进行数值计算，还可以对整个系统进行联合仿真。作为世界著名的商用低频电磁场有限元软件之一，Ansoft在各个工程电磁领域都得到了广泛的应用。本文采用Ansoft Maxwell 14进行电磁催泪风暴系统弹药的电磁运动仿真。

根据文献［9］可以知道，二维轴向瞬态磁场满足的齐次波动方程为：

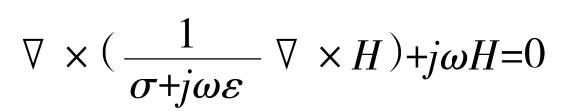
式中，σ是介质的电导率，ε是介质的介电常数，μ是介质的磁导率。

Maxwell就可以根据此微分方程进行数值求解，然后经过转化得到磁场的各种物理量。

为了便于确定弹药引信的参数，结合现阶段同类武器基本参数，将系统的发射单元参数作表2设置：

表2 系统发射单元参数

根据上述系统参数，建立Ansoft Maxwell模型如图3所示（由于系统设置隔磁材料，假设驱动线圈1通电时，驱动线圈2不会对系统磁场有影响，故驱动线圈2可省略不建）。

由于模型是轴对称形式，为了减少计算资源，采用柱面坐标。

为了模拟无限元边界，将边界条件设置为气球边界。

仿真时间参数方面，太大会占用计算资源，结合弹体出管的时间，设置为1 ms。

计算步长的选择需要慎重，太小可能不能计算收敛，太大计算精确度会降低，结合仿真时间，将计算步长设置为0.01 ms。

在Maxwell中，可以将需要优化的参数进行参数化处理，从而将其最优值找出，因此，将线圈匝数n和间距d分别做参数化处理，进行二维瞬态仿真。

图3 Maxwell模型图

3.2 仿真过程

仿真过程图如图4～图6所示。

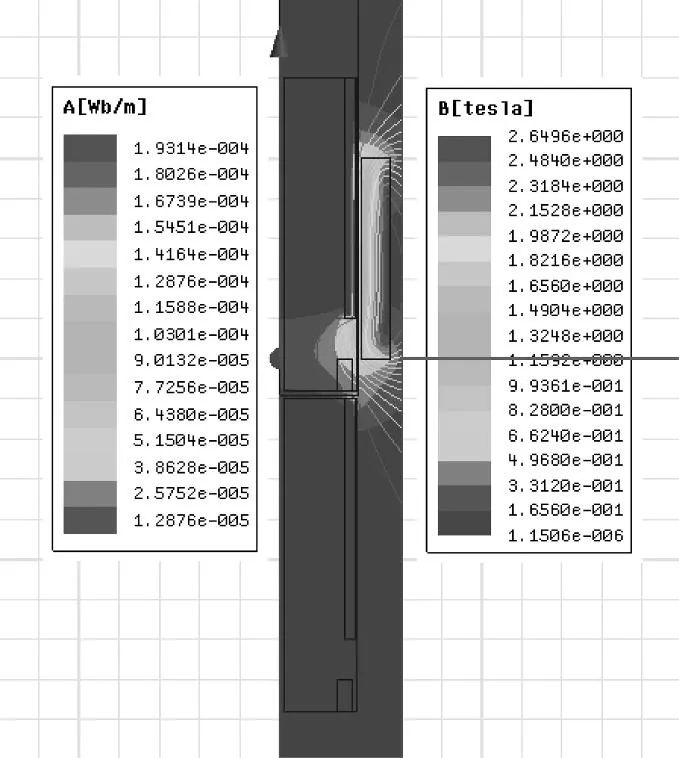
图4 系统在0.01 ms时的磁场分布

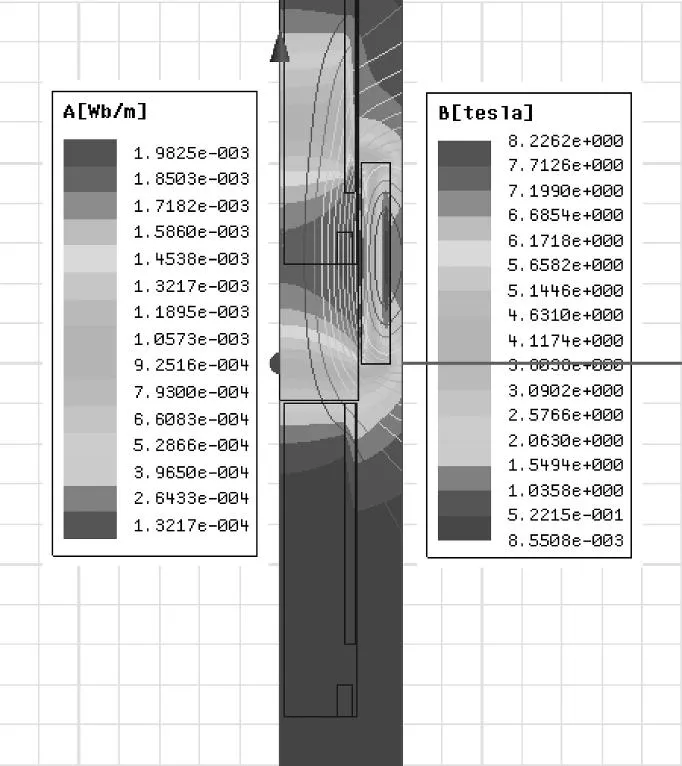
图5 系统在0.50 ms时的磁场分布

图6 系统在1.00 ms时的磁场分布

3.3 仿真结果

将匝数n参数化，可得到在不同匝数时引信1的感应电压的曲线如下页图7所示，弹药1的速度如下页图8所示。

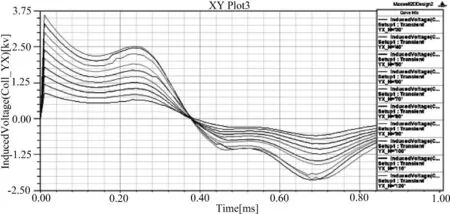
图7 在不同匝数时引信1的感应电压

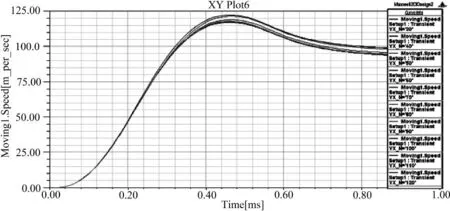
图8 在不同匝数时弹药1的速度

取引信线圈匝数为100，将引信线圈间距d参数化，可得到1弹发射时，在不同间距下引信2的感应电压的曲线如图9所示，弹药1的速度如图10所示。

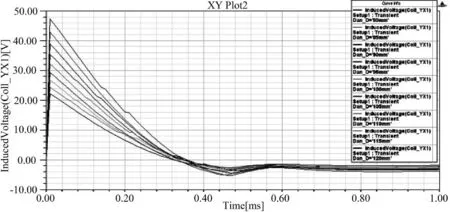
图9 在不同间距下引信2的感应电压

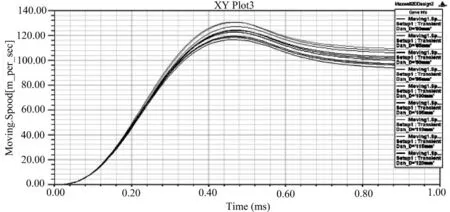
图10 在不同间距下弹药1的速度

3.4 结果分析

结果分析：从图7可以看出：当引信线圈匝数超过100（包含100）时，引信线圈感应电压超过3 kV，可以稳定发火。从图8可以看出，当取引信线圈匝数为100时，引信1和2相距超过80 mm（即弹药最小长度）时，引信2峰值电压不超过100 V，远远小于1.2 kV，保证了引信2不发火。而图9、图10可看出在引信符合要求的情况下，弹药出口速度可达100 m/s左右，符合作战需要。因此，在文中给定系统参数下，引信线圈最优匝数为100匝，最优位置为紧靠弹体最外圈，相邻引信最小间距即弹药最小长度为82 mm。

4 结束语

本文明确了简易电磁引信的发火电压标准，仿真分析了引信的各项参数，旨在为电磁催泪风暴系统引信设计提供一个合适方案，为下一步搭建实验平台提供引信的实现方法。

［1］王 莹，肖 峰.电炮原理［M］.北京：国防工业出版社，1995：93-97.

［2］于海龙.金属风暴武器发射动力学研究［D］.南京：南京理工大学动力工程学院，2008.

［3］王 莹，马富学.新概念武器原理［M］.北京：兵器工业出版社，1996：15l-152.

［4］严 璋，朱德恒.高电压绝缘技术［M］.北京：中国电力出版社，2002.

［5］Mason J H.The Deterioration and Breakdown of Dielectrics Resulting from internal Discharge［J］.Proceedings of the IEEE，1951：44-59.

［6］Bhalla M S，Craggs J D.Measurement of Ionization and Attachment Coefficients in SF6 in Uniform Fields［J］. Proceedings of the Physical Society，1962（80）：151-160.

［7］卡兰塔罗夫П Л，卡伊塔林Л.电感技术手册［S］.莫斯科：动力原子能出版社，1985.

［8］赵 博，张洪亮.Ansoft12在工程磁场中的应用［M］.北京：中国水利水电出版社，2007.

［9］赵 博，张洪亮.Ansoft12在工程磁场中的应用［M］.北京：中国水利水电出版社，2007：48.

Fuse Simulation of Electromagnetic Launch Style Tear Weapon System

YANG Feng
（Engineering University of Armed Police Force，Xi'an 710086，China）

The structure and principles of electromagnetic launch style tear weapon system are introduced.Applying the numerical analysis method to determine the standard of fuze ignition voltage，using the Maxwell electromagnetic simulation software to create two transmitting unit model，and through analysis，the paper gets the optimal location，best number of turns of the coil fuze and the minimum spacing parameter.A better solution to determine the electromagnetic induction type fuze is provided.

electromagnetic launch，electromagnetic induction，fuse，simulation

TJ43

A

1002-0640（2014）10-0179-04

2013-08-09

2013-10-07

杨 风（1991- ），男，湖南永州人，硕士研究生。研究方向：非致命武器。