复合材料Ⅰ+Ⅱ混合型周期平行裂纹尖端场

余路娟，张雪霞，赵文彬，李 婵(太原科技大学应用科学学院，太原 030024)

近年来，学者对共线周期裂纹尖端场问题做了大量研究[1-6]，而对于周期平行裂纹问题的研究相对较少。Hao[7]利用共形映射方法研究了含周期平行裂纹无限介质的弹塑性问题，得到了裂纹尖端的应力强度因子。Pak和Goloubeva[8]利用分布位错法对含双周期阵列平行裂纹压电材料的电弹性质进行了量化分析，给出了周期平行裂纹在反平面载荷作用时裂纹尖端磁场强度因子。Sanada等[9]用傅立叶变换，研究了层板玻璃纤维增强复合材料中含有周期平行裂纹时的情形，得到应力强度因子。Chen等[10]利用奇异积分方程，在无穷远处对称拉伸载荷的作用下对含周期平行裂纹无限介质的平面问题进行了研究，给出其级数形式的裂纹尖端应力强度因子。肖俊华和蒋持平[11]利用复应力函数的奇异性分析和双曲函数的周期性质确定应力函数的形式，推导了无限大各向同性弹性体中周期张开型平行裂纹问题应力强度因子的闭合解。贾红刚和聂玉峰[12]采用复变方法和待定系数法对正交各向异性纤维增强复合材料板的周期张开型平行裂纹尖端附近的应力场进行力学分析，在无穷远处对称拉伸载荷的作用下给出周期张开型裂纹尖端的应力强度因子及应力场的解析表达式。但是，所有这些结果都是在无穷远处受力得到的，未能研究裂纹面作用力下的周期平行裂纹尖端场问题。另外这些研究结果都未能很好地体现裂纹分布的周期性。因此，寻求能够更好地反映实际裂纹分布周期性的裂纹尖端场的解析解对于断裂理论研究和工程应用都有重要的意义。

本文利用复变函数方法研究了裂纹面均匀载荷作用下的正交各向异性复合材料板周期平行裂纹尖端场问题，得到Ⅰ+Ⅱ混合型周期平行裂纹尖端附近的应力强度因子和应力场的解析表达式。所得结果便于计算，对于复合材料断裂理论研究具有重要意义。

1 力学模型

本文讨论无限大线弹性正交各向异性纤维增强复合材料板Ⅰ+Ⅱ混合型裂纹尖端场问题。如图1所示，复合材料板含相距为ω、裂纹长为2a的周期平行裂纹，在裂纹上下表面受均匀分布载荷σ和τ作用，2个坐标轴平行于正交各向异性体的材料弹性主方向。

图1 混合型周期平行裂纹

正交各向异性板裂纹尖端应力场问题归结为求解下列偏微分方程的边值问题[11，13]:

(1)

假设应力函数：

U=U[x+s(y-nω)+inω](n=0,±1,±2…)

(2)

将式(2)代入控制方程式(1)，得到特征方程为：

b11s4+(2b12+b66)s2+b22=0

(3)

这是一个双二次方程，其判别式为:

当△>0时，特征方程(3)的解为[13]:

(4)

当△<0时，特征方程(3)的解为[13]:

(5)

若记：

zj=x+sj(y-nω)+nωi=xj+iyjj=1,2

(6)

利用公式(6)，控制方程可化为广义重调和方程，所以由复变函数理论可知控制方程有实值解析解，设:

(7)

根据应力和应力函数的关系，应力场公式可写为[13]：

(8)

2 周期性Ⅰ+Ⅱ混合型裂纹尖端应力场

因为边值问题(1)的偏微分方程和边界条件都是线性的，所以根据叠加原理，边值问题(1)可转化为下边两个边值问题(9)和(10)解的和，即周期性Ⅰ+Ⅱ混合型裂纹问题转化为周期性Ⅰ型和Ⅱ型裂纹问题。

(9)

(10)

利用待定系数法[13]分别解边值问题式(9)和式(10)，可得周期平行裂纹尖端附近的应力场。考虑到应力-应变关系及偏导数的加法原理，叠加原理对于应力场仍然适用，有：

σx,mix=σx,Ⅰ+σx,Ⅱσy,mix=σy,Ⅰ+σy,Ⅱ

τxy,mix=τxy,Ⅰ+τxy,Ⅱ

(11)

2.1 周期性Ⅰ型裂纹尖端场分析

为了求解边值问题(9)，选取如下Westergaard应力函数[11]：

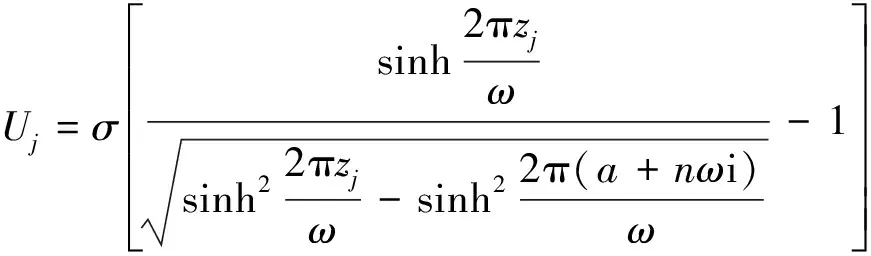
(12)

令zj-(a+nωi)=x+sj(y-nω)+nωi-

(a+nωi)=r(cosθ+sjsinθ)

则在裂纹尖端附近，当极径r→0时，有:

(13)

其中KⅠ为Ⅰ型裂纹的应力强度因子[12]。

利用待定系数法[13]解边值问题式(9)，可得周期平行Ⅰ型裂纹尖端附近的应力场解析表达式为：

(14)

2.2 周期性Ⅱ型裂纹尖端场分析

为了求解边值问题式(10)，选取如下Westergaard应力函数[11]：

(15)

当△>0时，将式(4，8，15)代入式(10)中的边界条件，可得：

(16)

当△<0时，将式(5，8，15)代入式(10)中的边界条件，可得：

(17)

将式(16)，(17)分别代入到式(7)中得到满足控制方程和边界条件的实值解析解U，从而偏微分方程边值问题(10)有解。

Ⅱ型裂纹的应力强度因子KⅡ定义为:

(18)

令zj-(a+nωi)=x+sj(y-nω)+nωi-

(a+nωi)=r(cosθ+sjsinθ)

则在裂纹尖端附近，当r→0时，有:

(19)

将式(4，16，19)和式(5，17，19)分别代入到式(8)，可得周期平行Ⅱ型裂纹尖端附近的应力场解析表达式为：

(20)

2.3 周期性Ⅰ+Ⅱ混合型裂纹尖端场分析

2.3.1 应力强度因子

按照sih[14]关于混合型裂纹应力强度因子的定义，我们可以得到Ⅰ+Ⅱ混合型周期平行裂纹的应力强度因子为:

(21)

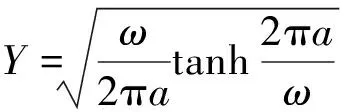
图2 形状因子Y随ω的变化曲线

2.3.2 周期平行裂纹尖端应力场

由式(11)、式(14)和式(20)可得周期平行Ⅰ+Ⅱ混合型裂纹尖端附近的应力场解析表达式为：

3 结论

研究了裂纹面内均匀载荷作用下的正交各向异性复合材料板周期平行裂纹尖端场问题。利用复变函数方法，将力学问题化为偏微分方程边值问题，再根据叠加原理，将偏微分方程边值问题化为Ⅰ型和Ⅱ型两个边值问题来求解。通过构造适当的Westergaard应力函数，将周期平行裂纹尖端应力场问题化为单一裂纹尖端应力场问题，再利用复变函数方法、待定系数法，借助边界条件，得到周期平行裂纹尖端场问题的解。

(1) 得到周期平行裂纹Ⅰ型、Ⅱ型、Ⅰ+Ⅱ混合型裂纹尖端应力强度因子的解析表达式。由于平行裂纹的周期性分布，应力强度因子的大小取决于形状因子，当裂纹间距趋于无穷大时，应力强度因子退化为含单个中心裂纹时的结果。

(2)得到周期平行裂纹Ⅰ型、Ⅱ型、Ⅰ+Ⅱ混合型裂纹尖端应力场的解析表达式。

参考文献：

[1] HAO T H.Multiple collinear cracks in a piezoelectric material[J].International Journal of Solids and Structures，2001，38：9201-9208.

[2] HWU C.Collinear cracks in anisotropic bodies[J].International Journal of Fracture，2001，52(4)：239-256.

[3] ERDOGAN F，OZTURK M.Periodic cracking of functionally graded coatings[J].International Journal of Engineering Science，1995，33(15)：2179-2195.

[4] HAUSLEX C，GAO C F，BALKE H.Collinear and periodic electrode-ceramic interfacial cracks in periodic-electric biomaterials[J].Journal of Applied Mechanics，2004，71(4)：486-492.

[5] CHEN Y Z.Collinear crack problem for a strip of functionally graded materials in anti-plane elasticity[J].Chinese Quarterly of Mechanics，2006，27：7-13.

[6] 郭俊宏，卢子兴.含周期性裂纹正交各向异性板平面问题的应力场分析[J].复合材料学报，2010，27(1)：162-167.

[7] HAO T H.An exact solution of the anti-plane parallel periodical transverse crack field in a bimaterial infinite plane[J].International Journal of Fracture，1991，47(3)：49-51.

[8] PAK Y E，GOLOUBEVA E.Electroelastic properties of cracked piezoelectric materials under longitudinal shear[J].Mechanics of Materials，1996，24(4)：287-303.

[9] SANADA K，SHINDO Y，UUDA S.Stress intensity factors for glass-fiber reinforced plastics with an infinite row of parallel cracks at low temperatures[J].Theoretical and Applied Fracture Mechanics，1998，28(3)：183-196.

[10] CHEN Y Z，LIN X Y.Periodic group crack problems in an infinite plate[J].International Journal of Solids and Structures，2005，42：2837-2850.

[11] 肖俊华，蒋持平.周期张开型平行裂纹问题研究[J].力学学报，2007，39(2)：27-282.

[12] 贾红刚，聂玉峰.正交各向异性板周期张开型平行裂纹的应力分析[J].兰州理工大学学报，2012，38(4)：169-172.

[13] 杨维阳，李俊林，张雪霞.复合材料断裂复变方法[M].北京：科学出版社，2005.

[14] SIH G C，LIEBOWITZ H.Mathematical theories of brittle fracture[M].New York：Academic Press，1968.