基于改进粒子群算法的分数阶系统辨识方法

王 强，赵志诚，桑 博(太原科技大学电子信息工程学院，太原 030024)

分数阶微积分与整数阶微积分诞生于同一时期，距今已有三百多年的历史。随着计算机技术的不断发展，分数阶微积分理论应用到了许多研究领域，如：电化学[1]，热力学[2]，生物学[3]，控制理论[4]等。研究表明，用分数阶微积分对实际动态对象和过程建模的好处很明显，分数阶模型具有更低的阶数，更少的参数，更高的建模精度等优点[5]，而且传统的整数阶系统模型是无法代替分数阶系统模型的[6]。目前对于分数阶系统辨识的研究尚处于初始阶段，没有统一的辨识方法。由于分数阶微积分的物理意义尚不能确定，目前几乎所有的分数阶系统辨识方法均不考虑模型结构参数的辨识，均是通过先验知识或者整数阶模型假设分数阶模型结构参数。文献[7]通过极大似然算法得到等效准则函数，将参数辨识问题转化为参数优化问题，模型误差主要集中在低频段；文献[8]提出了基于主元分析的分数阶系统子空间辨识方法，文献[9]基于分数阶Riemann-Liouville定义把调制函数方法扩展到分数阶系统辨识，计算量较大。文献[10]对含有一个或者两个伪极点的分数阶模型结构提出一种辨识方法，把一个无限维问题转化到有限维范围，但不能向更多伪极点分数阶模型推广。

本文提出一种基于改进的粒子群算法实现分数阶系统辨识的方法，可实现模型参数和阶次同时辨识。辨识精度高，而且易于编程实现，在有输出随机干扰的情况下也能辨识到精确的结果。

1 分数阶数学描述

分数阶微积分的发展经历了一个漫长的过程。它可以看作是整数阶微积分的推广。

1.1 分数阶微积分定义

在分数阶微积分理论发展过程中，出现了多种分数阶微积分的定义。常用的有Cauchy定义，Riemann-Liouville定义，Grumwald-Letnikov定义。

Cauchy分数阶积分定义：

(1)

式中，q为分数阶积分阶次，C为f(t)单值与解析开区域的光滑曲线，Γ为伽马函数。

Riemann-Liouville分数阶积分定义为：

(2)

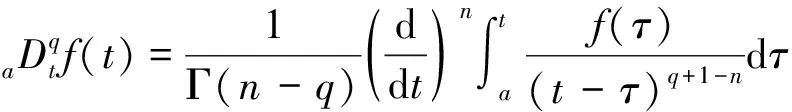
(3)

(4)

式中，h为步长，[X]表示对X的取整。当q>0，该式表示分数阶微分；当q<0，该式表示分数阶积分。

1.2 分数阶系统的数学模型

分数阶系统就是利用分数阶微分方程来描述其动态特性的系统。线性分数阶SISO系统的微分方程一般表达式：

anDαny(t)+an-1Dαn-1y(t)+…+a0y(t)=

bmDβmu(t)+bm-1Dβm-1u(t)+…+b0u(t)

(5)

式中，ai、bi为实数，微分阶次αi、βi可以为小数或者分数，u(t)为系统输入信号，y(t)为系统输出信号。在零初始条件下，其传递函数表达式为：

(6)

目前，辨识一般的分数阶系统是很困难的，因为系统的阶数很难确定。文献[11]提出连续阶次分布的概念，把分数阶系统一般表达式转化成公因子阶次表达式：

anDnαy(t)+an-1D(n-1)αy(t)+…+a0y(t)=

bmDmαu(t)+bm-1D(m-1)αu(t)+…+b0u(t)

(7)

式中，α为公因子阶次。

2 权值自适应粒子群算法

2.1 基本粒子群算法

粒子群优化算法采用“群体”和“进化”的概念，依据个体的目标函数值大小来确定最优解。

假设N维空间中，m个粒子组成一个群体，第i个粒子的位置记为Xi=(xi1，xi2，…，xiN)，其所经历的最好位置记为pbest=(pi1，pi2，…，piN)，运动速度记为Vi=(vi1，vi2，…，viN)，全局极值gbest=(gi1，gi2，…，giN)，则在迭代过程中，粒子按照式(8)、(9)更新自身速度与位置：

(8)

(9)

式中，i=1，2，3…，m；n=1，2，3…，N；c1、c2为学习因子，rand1、rand2是两个相互独立的0到1之间的随机数。

式(8)表明粒子的速度更新由当前状态、自身经验、和社会学习三部分组成，不仅平衡了局部和全局搜索能力，避免局部极小，同时使粒子间信息共享，最终到达最优位置。将粒子的位置Xi带入目标函数就得到相应的适应值fi=f(Xi).

2.2 权值自适应策略

基本粒子群算法存在容易陷入局部最优的问题，而且ω的大小会影响到算法的全局和局部搜索能力，因此可以通过调整惯性权值ω来改进算法。

本文以所有粒子当前目标函数值的平均值作为粒子评价指标，把粒子群分为三个不同的子种群，每个子群根据粒子的目标函数值自适应的调整惯性权值ω，进而增强种群多样性以提高算法的全局和局部搜索能力。

假设m个粒子的粒子群，当前所有粒子目标函数值的平均值记为favg：

(10)

式中，fi为粒子的当前适应值。

惯性权值ω值的自适应策略如下：

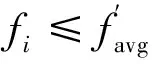
(11)

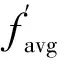
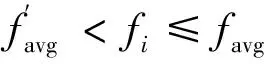
(12)

式中，ωmax为ω的最大值，iter为当前迭代次数，itermax为允许迭代最大次数。

3)当favg

(13)

式中，k1用来控制ω的上限，k1越大ω的上限越大，为使式(13)的ω值能够大于1，本文取k1=1.5，则ω∈(0.5，1.1)；k2控制式(13)的调节能力，k2过大，ω会迅速越小，使得算法的全局搜索能力不足，k2过小，ω变化不明显，容易导致算法陷入局部最优，本文选取k2=0.9.

3 分数阶系统辨识

文中将改进的粒子群算法应用到分数阶系统辨识过程中，辨识步骤如下：

1)确定搜索向量，即待辨识的参数，包括模型参数和阶次。

2)选择目标函数。将单位阶跃信号加入到实际系统中，得到输出响应y(t)，将单位阶跃信号加入到待辨识模型中，得到输出响应为yM(t)，选取算法的适应度函数为，

3)算法初始化。初始化算法相关参数，产生随机搜索向量。

4)确定截止条件。截止条件选择最大迭代次或者目标函数值。

4 仿真实例

为检验所提分数阶系统辨识方法的有效性，针对几种不同模型做如下仿真，并考虑了无输出干扰和有输出干扰两种情况。仿真取迭代次数100次为算法截止条件，即itermax=100.算法中参数设定如下：c1=c2=1.5，ωmin=0.4，ωmax=0.9.粒子初始化范围在区间(0，3)内。假设辨识的模型结构为：

仿真过程中，将本文方法与文献[12]的方法进行比较，为避免算法初始值对比较结果的影响，两种辨识方法采用同一组初始值。

1)输出响应无干扰，即在理想情况下通过上述方法对系统进行辨识。

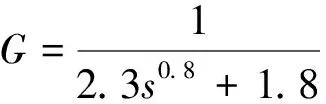
利用本文方法得到的系统辨识结果为：目标函数值f=3.086 2e-28，a1=2.300 0，a0=1.800 0，β=0.800 0.模型的单位阶跃响应如图1，目标函数值的对数随迭代次数变化曲线如图2.由图可见，辨识模型与实际系统的单位阶跃响应曲线高精度拟合，算法迭代20次时，辨识的误差值为0.001 6，文献[12]辨识的误差值为1.214 8，由此表明，本文方法仅需较少的迭代次数就可辨识到期望的系统模型。

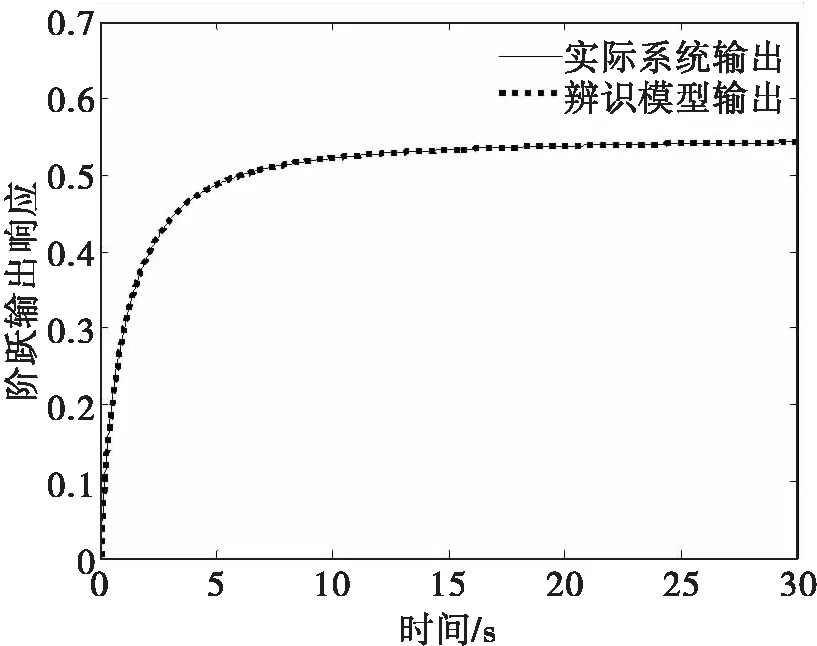
图1 模型Ⅰ及其辨识模型的阶跃响应

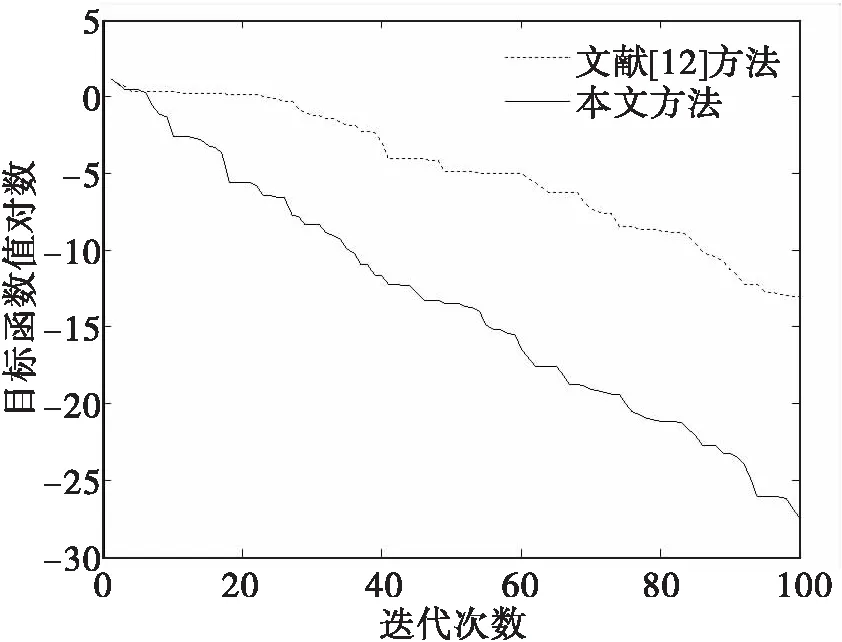
图2 模型Ⅰ目标函数值的对数变化曲线

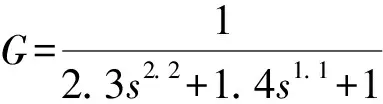
该模型为成比例分数阶系统模型，取α=2β，利用本文方法得到的系统辨识结果为：

f=7.684 6e-23，a2=2.300 0，a1=1.400 0，a0=1.000 0，β=1.100 0.如图3所示，实际系统与辨识模型的单位阶跃响应曲线几乎完全拟合。同样，由图4可见，对于成比例分数阶系统，本文方法优于文献[12]的方法。

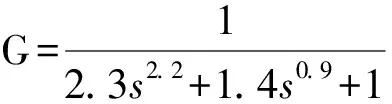
该模型为不成比例分数阶系统模型。利用本文方法得到的系统辨识结果为：目标函数值f=4.756 4e-20，a2=2.300 0，a1=1.400 0，a0=1.000，α=2.200 0，β=0.900 0，其阶跃响应及目标函数值变化如图5、6所示。由图可见，实际模型与辨识模型的单位阶跃响应曲线高精度拟合。对于不成比例分数阶系统，本文方法优于文献[12]的方法，能够得到很好的辨识效果。

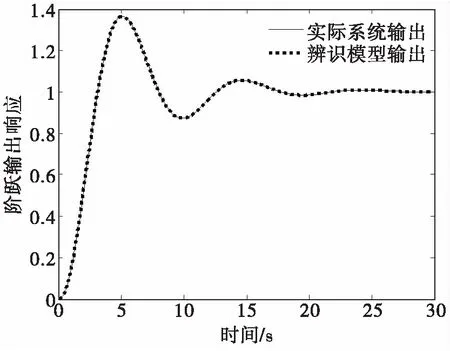
图3模型Ⅱ及其辨识模型的阶跃响应

Fig.3StepresponseofmodelⅡanditsidentificationmodel

图6 模型Ⅲ目标函数值的对数变化曲线

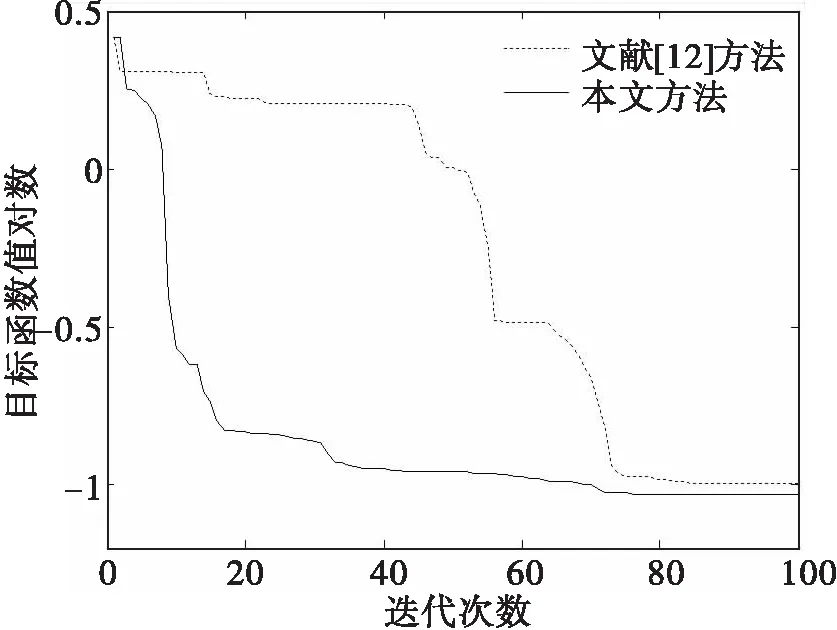
图8 有干扰时模型Ⅲ目标函数值的对数变化曲线

2)输出响应有干扰，在输出响应y(t)上叠加-0.03～0.03的随机干扰。下面仅对模型Ⅲ进行有随机干扰的仿真分析。

利用本文方法得到的系统辨识结果为：目标函数值f=0.091 0，a2=2.287 0，a1=1.366 8，a0=0.999 3，α=2.187 6，β=0.891 5.如图7，有随机干扰的实际系统单位阶跃响应与辨识模型的单位阶跃响应曲线基本一致。同样，由图8表明，在输出响应有干扰的情况下，本文方法明显优于文献[12]方法，在迭代到10次之后，本文方法辨识的误差值明显小于文献[12]方法辨识的误差值。

5 结论

按照粒子目标函数值的不同，将粒子群分为三个子种群，引入惯性权值自适应律来改进基本粒子群算法，并利用改进的粒子群算法提出一种分数阶系统辨识方法，实现对分数阶系统的模型参数和阶次参数同时辨识。方法选取实际系统与辨识系统的输出误差平方和为目标函数。仿真结果表明，本文方法可有效辨识成比例和不成比例分数阶系统，算法辨识精度较高。

参考文献：

[1] OLDHAM K B.Fractional differential equations in electro-chemistry[J].Advances in Engineering Software，2010，41(1)：9-12.

[2] GABANO J D，POINOT T.Fractional modeling and identification of thermal systems[J].Signal Processing，2011，91(3)：531-541.

[3] MAGIN R L.Fractional calculus models of complex dynamics in biological tissues[J].Computers & Mathematics with Applications，2010，59(5)：1586-1593.

[4] 桑海，赵志诚，孟香，等.交流伺服系统的一种PIλDμ控制器设计方法[J].太原科技大学学报，2013，34(6).

[5] 苏密勇，谭永红，王子民，等.同元次分数阶模型的一种具有稳定约束的频域辨识算法[J].四川大学学报：工程科学版，2012，44(2)：130-134.

[6] ZHANG X，CHEN Y Q.Remarks on fractional order control systems[C]∥American Control Conference (ACC).Montreal，Canada，2012：5169-5173.

[7] LI W，PENG C，WANG Y.Identifying the fractional-order systems with frequency responses：A maximum likelihood algorithm[C]∥International Conference on Radar.Cheng Du，China，2011，2：1943-1948.

[8] ZENG L，CHENG P，YONG W.Subspace identification for commensurate fractional order systems using instrumental variables[C]∥Proceedings of the 30th Chinese Control Conference (CCC).Yantai，China，2011：1636-1640.

[9] LIU D Y，LALEG-KIRATI T M，GIBARU O，et al.Identification of fractional order systems using modulating functions method[C]∥American Control Conference (ACC).Washington DC，USA，2013：1679-1684.

[10] NAZARIAN P，HAERI M.Identification of fractional order model structures using conversion of infinite terms of a response to finite terms[C]∥7th International Conference on Electrical and Electronics Engineering (ELECO).Bursa，Turkey，2011:391-395.

[11] HARTLEY T T，LORENZO C F.Fractional-order system identification based on continuous order-distributions[J].Signal processing，2003，83(11)：2287-2300.

[12] MAITI D，CHAKRABORTY M，KONAR A.A novel approach for complete identification of dynamic fractional order systems using stochastic optimization algorithms and fractional calculus[C]∥International Conference on Electrical and Computer Engineering.Dhaka，Bengal，2008：867-872.