基于几何速度稳定性的最优觅食微粒群算法

樊卫兵(山西中医学院，太原 030024)

微粒群算法[1-2](Particle Swarm Optimization，PSO)是一种模拟鸟群飞行、鱼群游动等社会行为的群体智能优化算法，该算法由于速度较快、编程简单，现已广泛应用于许多实际问题[3-5]。

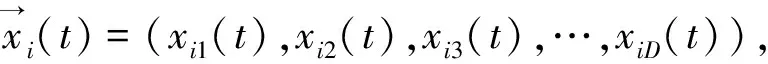
xij(t+1)=xij(t)+vij(t+1)

(1)

vij(t+1)=wvij(t)+c1r1(pij(t)-xij(t))+
c1r1(pgj(t)-xij(t))

(2)

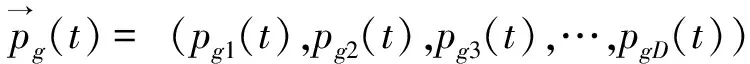
标准微粒群算法较为简单，它仅仅粗步模拟了鸟群的觅食行为，但经过自然界数以万年的发展，鸟类一般都具有些特定的觅食模式，比如最优觅食策略。为此，Y Chu等人将最优觅食策略引入微粒群算法，提出了最优觅食微粒群算法[7-8]。本文针对最优觅食微粒群算法，讨论其稳定性条件，并给出了惯性权重的随机选择策略。

1 最优觅食微粒群算法

经过亿万年的演化，动物的食物源一般均不是唯一的，因此，在觅食过程中就有一个食物选择的问题。经过动物学家的研究，我们发现动物在觅食过程中，鸟群总是选择最有利的食物，而不是最喜欢吃的食物[9]，这就是最优觅食策略，该策略表明，动物在选择食物时，总是趋于耗费更低的能量而获得更多地能量，以达到能效最优，从而提高生存概率。 在微粒群算法中，每个微粒都在搜索空间中觅食，它们一般倾向于搜索食物源较多的位置，而这一点显然与上述的最优觅食策略相悖。因此，从这个角度出发，我们将最优觅食策略引入微粒群算法。

由于适应值函数表示食物源的多寡，可定义微粒群中某一微粒i受到的能效吸引为它和其它个体的适应值差别与两个体之间距离的比值，即:

(3)

其中，Fik表示微粒i对微粒k的能效作用力，Fik>0表示微粒i受到微粒k的能效吸引，Fik<0表示微粒i能效排斥微粒k，Fik=0表示微粒i与微粒k处于能效平衡状态。称其它微粒对微粒i的最大能效作用力为Fi,max，即:

Fi,max=arg max{Fis(t)|s=1,2,…,D}

(4)

基于上述结论，Chu YF等人提出了下面的速度更新方式：

vij(t+1)=ωvij(t)+c2r2(pgj(t)-xij(t))+
c3r3(aij(t)-xij(t))

(5)

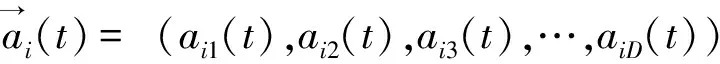
2 基于几何速度稳定性的参数选择

考虑如下动态系统：

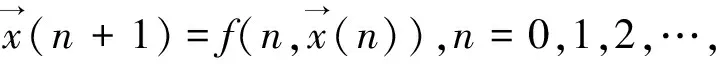
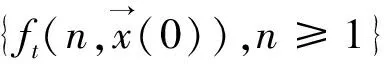
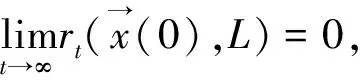
2)如果收敛具有指数速度，即存在正数θ<1和K1,K2使得:

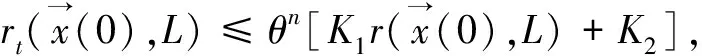
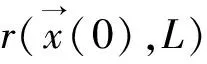
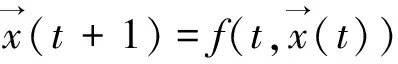
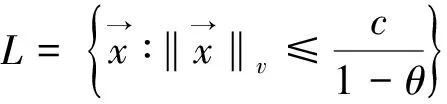
下面就利用上述定理来分析最优觅食微粒群算法的几何速度稳定性。为了方便起见，设φ2=c2r2，φ3=c3r3，φ=φ2+φ3，则最优觅食微粒群算法的速度与位置进化方程可改写为：

vij(t+1)=wvij(t)-φxij(t)+φ3aij(t)+φ2pgj(t)

xij(t+1)=wvij(t)+(1-φ)xij(t)+φ3aij(t)
+φ2pgj(t)

转换为矩阵形式：

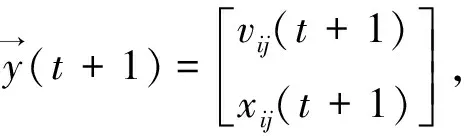
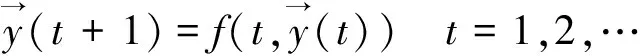
考虑欧式空间的∞范数，则有:

而

|φ3aij(t)+φ2pgj(t)|≤(c1+c2)·max{xmax,-xmax}

其中，[xmin,xmax]D为定义域空间，取c=(c1+c2)·max{xmax，-xmin},则定理中的c存在且非负。

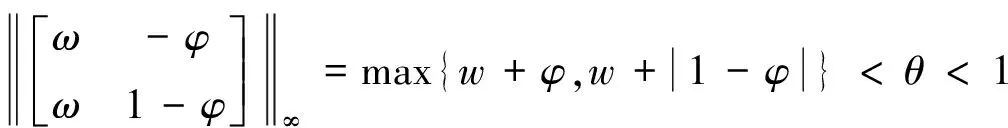
假设θ=0.9，此时可进行如下讨论：

1)当0<φ<0.5时，ω+φ<ω+1-φ<0.9<1，即0<ω<φ-0.1；

2)当0.5≤φ<1时，ω+1-φ<ω+φ<0.9<1，即0<ω<0.9-φ；

3)当φ>1时，不成立；

综上所述，ω和φ的参数选择为:

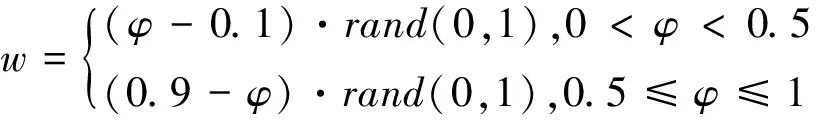
(6)

为了和其他的算法进行区别，因此将本文中的改进算法称为基于几何速度稳定性的最优觅食微粒群算法(optimal foraging particle swarm optimization with geometric speed stability，简称OFPSO_GSS).

下面给出具有几何速度稳定性的最优觅食微粒群算法(OFPSO_GSS)的流程：

1)依照初始化过程，对粒子群的随机位置和速度进行初始设定；

2)按照式(6)中得到的惯性权重ω进行设置；

3)利用最优觅食微粒群算法的进化方程更新各微粒的速度及位置向量；

4)计算每个微粒的适应值；

5)更新各微粒的个体历史最优位置与群体历史最优位置；

6)如未达到结束条件通常为足够好的适应值或达到一个预设最大迭代次数，则返回步骤2.

3 仿真实验

为了能提供更加准确的分析，考虑两种距离度量，分别为欧氏距离和逻辑距离，其欧氏距离定义为：

相应地，逻辑距离为：

dij=|j-i|

在算法比较中，考虑欧氏距离为度量标准的最优觅食算法(optimal foraging particle swarm optimization with Euclid distance，OFPSOED)、逻辑距离为度量的最优觅食算法(optimal foraging particle swarm optimization with logical distance，OFPSOLD)、标准微粒群算法(standard particle swarm optimization，SPSO)、带时间带时间加速常数的微粒群算法[11](MPSO_TVAC)及被动聚集微粒群算法(Particle swarm optimization with passive congregation，PSOPC)[12]进行比较，并选择如下5个典型的测试函数进行测试：

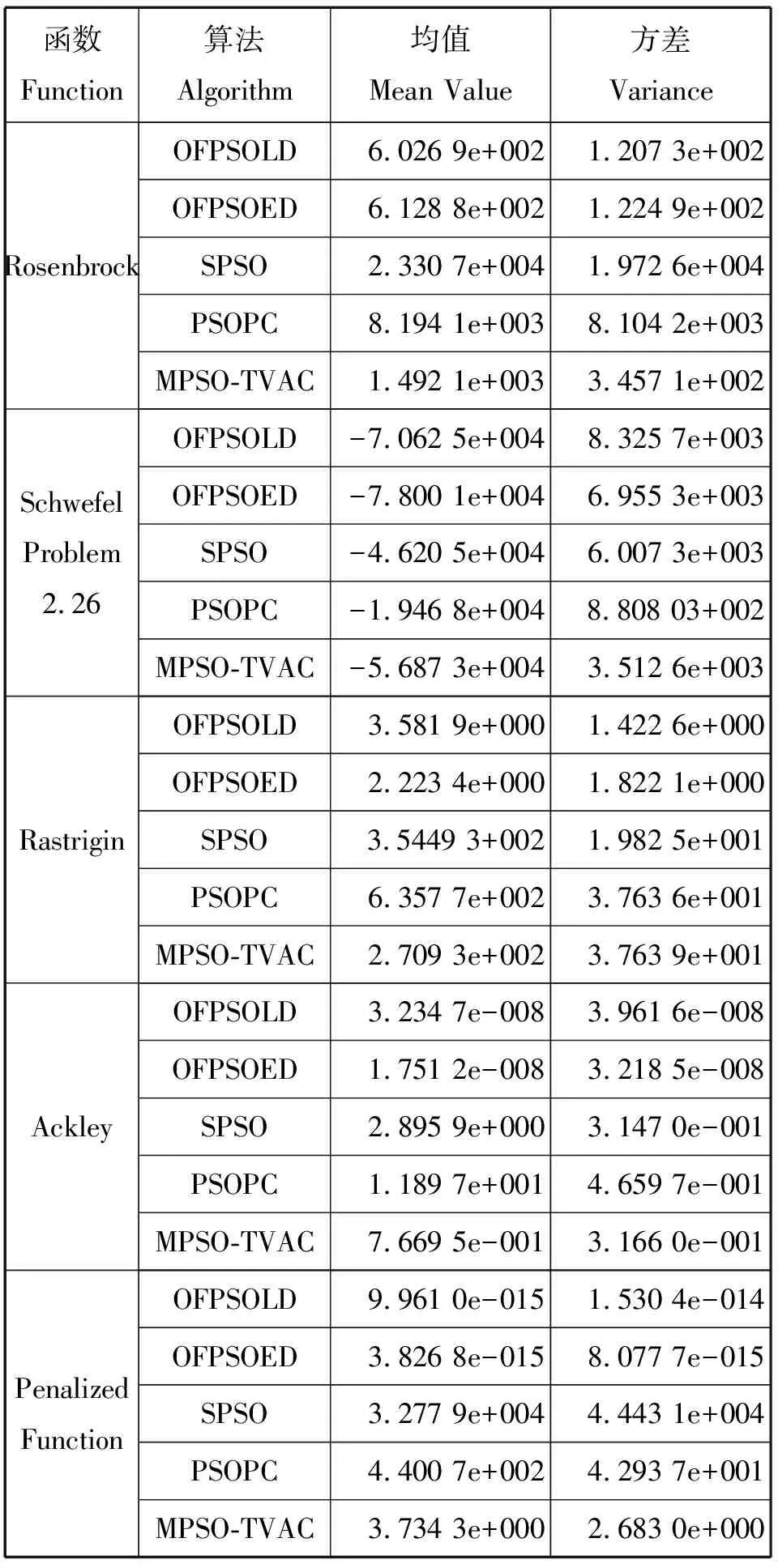
表1 300维算法性能比较

Rosenbrock Function：

Schwefel Problem 2.26 Function：

min(f2)=f2(420.968 7，…,420.968 7)=-418.982 9n

Rastrigin Function：

-5.12≤xi≤5.12,min(f3)=f3(0,…,0)=0.Ackley Function：

min(f4)=f4(0,…，0)=0

Penalized Function：

sin2(3πxi+1)]+(xn-1)2[1+sin2(2πx30)]}+

min(f7)=f7(1,…,1)=0,其中：

SPSO与OFPSO_GSS的加速度常数均为2.0，SPSO与MPSO_TVAC的惯性参数ω从0.9线性递减至0.4.而OFPSO_GSS的惯性权重按照公式(6)进行选择。对于MPSO_TVAC而言，其认知系数从2.5线性递减至0.5，而社会系数则从0.5线性递增至2.5.

表1为五个算法在五个测试函数中的性能比较，结果表明对于高维多峰优化问题，两种最优觅食微粒群算法都优于其它三种算法，并且欧氏距离为度量标准的最优觅食算法性能更佳。

4 结论

最优觅食微粒群算法是一种高效的改进微粒群算法，该算法通过引入动物的最优觅食策略，较为真实地模拟了动物的觅食行为。本文利用几何速度稳定性分析了最优觅食微粒群算法的稳定性，给出了稳定性条件。为验证其性能，本文选取了五个算法在5个典型测试函数下进行性能比较，仿真结果证明了该策略的有效性。

参考文献：

[1] KENNEDY J，EBERHART R C.Particle swarm optimization[C]∥Pro-ceeding of1995 IEEE International Conference on Neural Net-works.USA：New York：NY，1995.1942-1948.

[2] EBERHARTR C，KENNEDY J.A new optimizer using particle swarm theory[C]∥Proceedings of the Sixth International Symposiumon MicroMachine and Human Science.USA：New York，NY，1995.39-43.

[3] 郭研，李南，李兴森.多模式多资源均衡及基于动态种群的多目标微粒群算法[J].控制与决策，2013，28(1)：131-136.

[4] 江善和，纪志成，张日东，等.基于种群年龄模型的动态粒子数微粒群优化算法[J].系统工程理论与实践，2012，32(11)：2550-2556.

[5] 刘朝华，章兢，李小花，等.免疫协同微粒群进化算法的永磁同步电机多参数辨识模型方法[J].自动化学报，2012，38(10)：1698-1708.

[6] 崔志华，曾建潮.微粒群优化算法[M].北京：科学出版社，2011.

[7] CHU YF，CUI Z H.Neighborhood sharing particle swarm optimization[C]∥Proceedings of the 8th IEEE International Conference on Cognitive Informatics.Hong Kong，2009:521-526.

[8] CUI ZH，CHU Y F.Nearest neighbor interaction PSO based on small-world model[C]∥Proceedings of the 10 International Conference on Intelligent Data Engineering and Automated Learning.Spain，2009:633-640.

[9] 尚玉昌.行为生态学[M].北京：北京大学出版社，2001.

[10] 朱伟.时变离散动态系统的渐近稳定性和几何速度稳定性[J].应用科学学报，2004，22(2)：252-254.

[11] RATNAWEERA A，HALGAMUGE S K ，WATSON H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J].Transactions on Evolutionary Computation，2004，8(3)：240-255.

[12] HE S，WU Q H.A particle swarm optimizer with passive congregation[J].BioSystems，2004，78(1)：135-147.