弹塑性接触变形下的接触热导分形模型
2014-06-13马丽娜
马丽娜
(太原科技大学机械工程学院,太原 030024)
由于人们注意到接触热阻在实际工作中带来的各种问题的重要性,所以对接触热阻进行了大量的理论研究建模工作;Chang[1]提出同时考虑弹性和塑性变形,建立了CEB模型,但仍旧无法完整的阐述接触临界点的接触参数不连续的事实。文献[2-5]均指出,结合面的接触机制若只考虑完全弹性或完全塑性变形的情况或者同时考虑弹性、塑性变形都不可避免地存在着缺陷,因为结合面的真实接触历程必然要经历弹性、弹塑性和塑性变形三种变形阶段,正是基于此建立了相应的弹性、弹塑性、塑性三种变形机制下的分形模型。鉴于此,本文将研究建立考虑结合面弹性、弹塑性、塑性三种接触变形机制的接触热阻分形模型,并与文献[6]实验实例结果进行比较,以验证所建模型的正确有效性。
1 接触热阻
机械结构或系统中结合面是大量存在的[7],宏观上来看零件之间的结合面的接触是完全接触,但由于工程表面的微观不平,结合面两接触面之间的接触只是发生在某些微凸峰处,接触面积只是因为凸峰之间的接触变形而产生的,而其他的矮凸峰和凹谷处则存在空隙,当热流经过结合面时,主要的传热方式有[8-10]:(1)接触面之间的热传导;(2)通过间隙介质的热传导。由于间隙介质的导热系数与固体间的导热系数一般相差很大,即间隙介质的导热系数一般较结合面固体材料的导热系数小,因而会引起结合面附近热流发生改变,形成对热流的附加阻力,即接触热阻。当一定的热流通过接触面时,两接触表面之间会产生一个间断而又明显的温差。相对于零件材料对热流的阻力,接触热阻对热流的阻力更大更明显,与零件材料、接触面压力、粗糙度、介质等多种因素相关,进而导致了问题的复杂性[10]。

图1 接触面附近热流变化[9]Fig.1 Heat flux change near the contact surface
一般说来,在接触界面中,真实的接触面积即实际的接触面积是非常小的,文献[10]指出实际的接触面积只占名义接触面积的1%-10%,两个接触面之间的间隙如图2(a)所示。接触的表面一般情况下都处理成如图2(b)所示。在这个模型中,接触表面被假设成一组圆柱,半径是相当于实际接触面积,高度相当于表面的粗糙度,如图2(c)所示。源自该模型的等价的接触热导如式(1)所示[11]。

图2 接触热导理论模型图Fig.2 The theoritical model of contact thermal conduction
热分析中,接触热阻对热流的影响由接触系数h反映,其表达式为[11]:
(1)
式中:hc——接触面的等价接触热导;
δ——材料的表面粗糙度;
λ——材料的热导率;
λf——间隙介质的导热系数;
h0——实际接触面积的接触热导;
a——实际接触面积;
A——名义接触面积;
C——比例系数;
P为不同接触状态下的接触载荷。
(2)
将式(2)代入式(1)得:
(3)
结合面上实际接触面积的接触热导h0主要受材料的表面如被氧化的表层的影响,如图3所示。
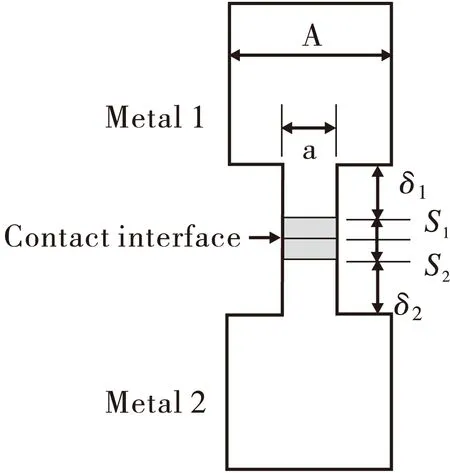
图3 表面的计算模型Fig.3 Calculation model for supposed surface layer
结合面上实际接触面积的接触热导h0为:
(4)
式中,S2、S1分别为图3中所假设的表面层的厚度。
将式(4)代入式(3)可以得到:
(5)
在真空介质下,λf=0,式(5)可以简化为:
(6)
2 结合面接触热导在不同接触变形机制下的理论分形模型
2.1 完全弹性接触变形机制下的接触热导模型
微凸体的变形在弹性范围内,一般采用赫兹接触理论来分析,则此时单个微凸体法向接触载荷为[12,14]:
(7)

式中:E1、E2——两接触材料的弹性模量;
v1、v2——两接触材料的泊松比。
根据文献[5,7]微凸体顶端的变形量w与微接触截面积a′的关系式以及微凸体曲率半径为:
(8)
(9)
将式(8)、(9)代入(7)可得:
(10)
微接触截面积为a′的接触点大小的分布函数[15-16]:
(11)
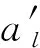

则整个结合面上所有产生弹性接触的微凸体的接触载荷为:
当分形维数D≠1.5时,
(12)
分形维数D=1.5时,
(13)
将式(12)、(13)代入式(6),则可以得到结合面上所有产生弹性接触的微凸体的接触热导为:
当分形维数D≠1.5时,

(14)
当分形维数D=1.5时,
(15)
2.2 完全塑性接触变形机制下的接触热导模型
微凸体法向变形量处于完全塑性变形的范围时,即δ≥76.4δc时[12](δc为微凸体从完全弹性变形过渡到弹塑性变形时的临界变形量),当微凸体即将处于完全塑性变形时,此时完全塑性变形阶段的单个微凸体,其塑性接触点的截面积a′与法向塑性接触载荷pp的关系为[10]:
pp=kσya=Ha=Ha′
(16)
式中:H——较软材料的硬度;
σy——较软材料的屈服强度。
则整个结合面上所有产生塑性接触的微凸体的法向接触载荷Pp为:

(17)
当分形维数D≠1.5时,
(18)
当分形维数D=1.5时,
(19)
将式(18)、(19)代入式(6),则可以得到结合面上所有产生塑性接触的微凸体的接触热导为:
当分形维数D≠1.5时,
76.4(2-D)/(1-D)·ψ(2-D)/2
(20)
当分形维数D=1.5时,
(21)
2.3 弹塑性接触变形机制下的接触热导模型
微凸体的变形量δc≤δ≤76.4δc时[12],微凸体的变形处于弹塑性过渡变形阶段,这一阶段的单个微凸体法向接触载荷为:
(22)
则整个结合面上弹塑性接触载荷为:

(23)
相应的,结合面上产生弹塑性接触的微凸体的接触热导为:
(24)
2.4 结合面上的总接触热导
结合面的法向接触载荷P为完全弹性、塑性接触及弹塑性接触载荷之和,即:
P=Pp+Pep+Pe
(25)
当分形维数D≠1.5时,
(26)
当分形维数D=1.5时,
(27)
将式(26)和(27)分别代入式(6)可得接触热导的表达式:
当分形维数D≠1.5时,
(28)
当分形维数D=1.5时,
(29)
3 结合面接触热导分形模型的仿真
为了验证该接触热导的分形理论模型的正确性,这里选择文献[6]的实验实例作为比较参照对象,即将本文的得到的理论模型的仿真结果与文献[6]实验结果进行比较。
文献[6]的实验实例条件为:常温常压、结合面之间的媒质为空气,两零件的材料均为304不锈钢,材料表面的加工方法未研磨方法,结合面相关参数如表1所示。

表1 表面相关参数Tab.1 The related parameters of surface
文献[6]的实验结果如图4所示。

图4 文献[6]接触热导实验值Fig.4 The experimental values of contact thermal conduction
本文所建模型的仿真计算结果如图5所示。
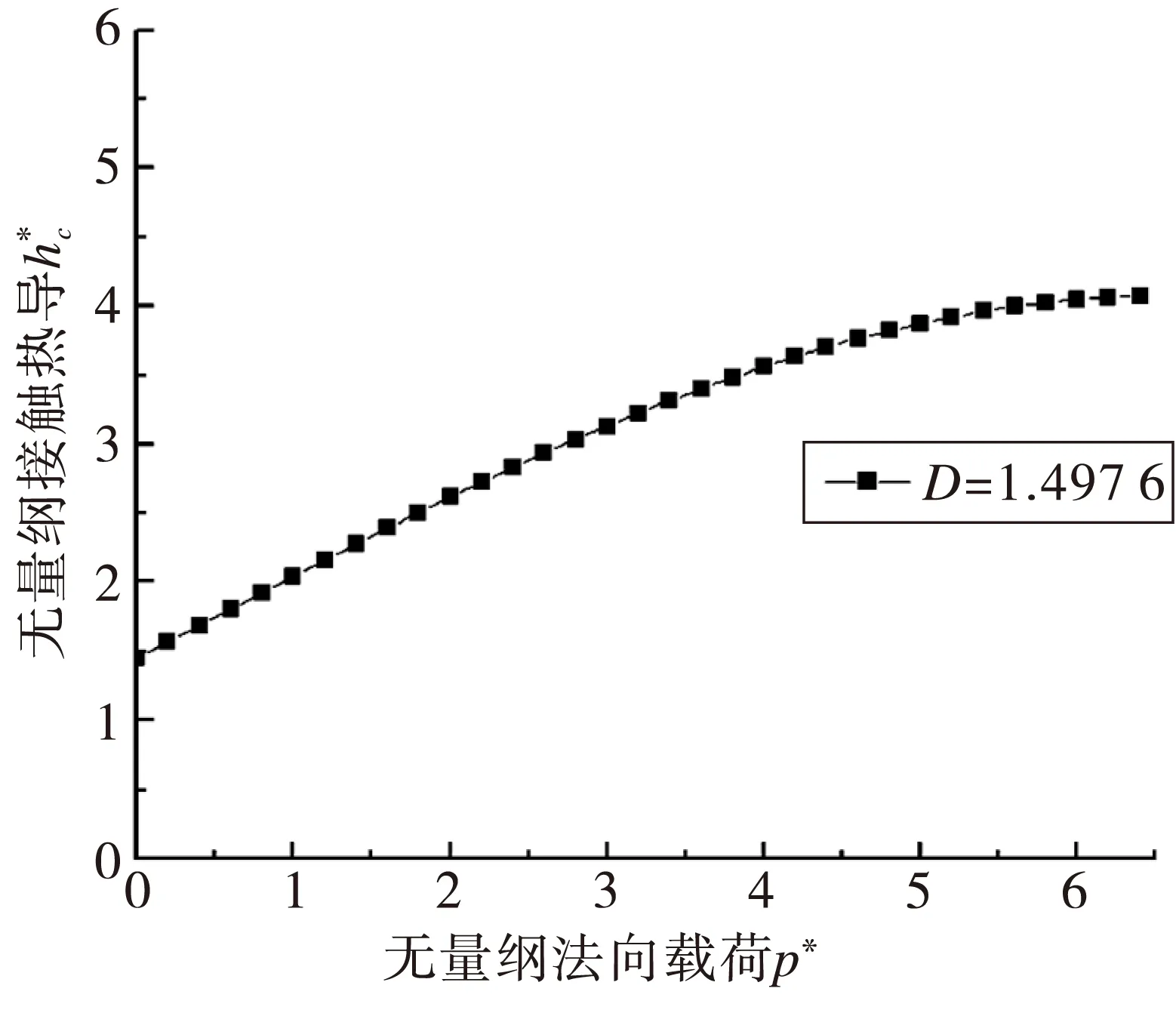
图5 接触热导仿真计算结果Fig.5 The results of contact thermal conduction
由图4与图5可以看出,模型的仿真计算结果与文献[6]的实验结果吻合较好,证明了本文所建模型的正确性。
4 结论
(1)建立了一种结合面接触热导的分形模型,它是作用在结合面上的法向载荷P的复杂非线性函数。
(2)接触热导与两零件材料性能参数——硬度H、复合弹性模量E*等有关。
(3)当结合面的压力增大时,接触热导会随着结合面压力的增大而增大,即接触热阻会随压力的增加而减小。
(4)分形维数D与接触热导之间的关系基本上是分形维数D越大,接触热导也越大,即接触热阻越小。
参考文献:
[1] TING-YUCHEN,WEI-JIUMMWEI,JHY-CHERNGTSAI.Optimum design of headstocks of precision Iathes[J].Internationgal Journal of Machine Tool Manufacture,1999,39:1961-1977.
[2] KOGUT L,ETSION I.Elastic-plastic contact analysis of asphere and a rigid flat[J].ASME:Journal of Applied Mechanics,2002,69(5):657-662.
[3] JACKSON R L,GREEN I.A finite element study of elastoplastic hemispherical contact against a rigid flat[J].ASME :Journal of Tribology,2005,127:343-354.
[4] CHUNG J C,LIN J F.Variation in fractal properties and Non-Gaussian distributions of microcontact between elastic-plastic rough surfaces with mean surface separation[J].ASME:Journal of applied mechanics-transactions,2006,73:143-152.
[5] 赵永武,吕彦明,蒋建忠.新的粗糙表面弹塑性接触模型[J].机械工程学报,2007,43(3):95-101.
[6] 赵兰萍,徐烈.低温真空下固体结合界面间接触热导的实验研究[J].中国空间科学技术,2003(1):51-55.
[7] 林黎柏.表面粗糙度微观接触力学的研究[D].台湾台南:国立成功大学,2006.
[8] MAJUMDAR A,TIEN C L.Fractal Network Model for Contact Conductance[J].ASME:Journal of Heat Transfer,1991,113:516-525.
[9] MAJUMDAR A,BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces[J].ASME:Journal of Tribology,1991,113(1):1-11.
[10] MAJUMDAR A,BHUSHAN B.Role of Fractal geometry in roughness charaterization and contact mechanics of surfaces[J].ASME:Journal of Tribology,1990,112(2):205-206.
[11] 尤晋闽,陈天宁.基于分形接触理论的结合面法向接触参数预估[J].西安交通大学学报,2011,45(9):1275-1280.
[12] 葛世荣,TONDER K.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80.
[13] 葛世荣,索双富.表面轮廓分形维数计算方法的研究[J].摩擦学学报,1997,17(4):354-361.
[14] 兰国生,张学良,丁红钦,等.基于分形理论的结合面改进模型[J].农业机械学报,2011,42(10):217-223,229.
[15] 顾慰兰,杨燕生.温度对接触热阻的影响[J].南京航空航天大学学报,1994,26(3):342-350.
[16] MAJUMDAR A ,BHUSHAN B.Fractal Model of Elastic-Plastic Contact Between Rough Surface[J].ASME:Journal of Tribology,1991,113(1):1-11.
[17] A MAJUMDAR,TIEN C L.Fractal Network Model for Contact Conductance[J].ASME:Journal of Heat Transfer,1991,113:516-525.
