二维环面网络的边容错哈密尔顿性

高晓慧，李 晶，谢秀梅

(1.太原科技大学应用科学学院，太原 030024；2.大同市广灵一中，山西 大同 037500)

1 背景介绍

直连网络是一种常见的网络拓扑结构，已经广泛应用于多处理器系统，多计算机系统以及集群系统中。随着并行计算机互连网络和VLSI技术的迅速发展，系统中的并行处理机越来越多，仍采用传统的网络互连结构已不能满足需求。于是人们对并行计算机互连网络拓扑结构进行了大量的研究[1-4]，并对其中的一些拓扑结构已研制出了相应的商用和研究用的并行计算机系统。网络是一种完全对称的直连网络拓扑结构，它具有很多优秀的网络特性[5]，如规则对称性，路径多样性以及良好的扩展性。因此它广泛应用于许多商用系统中，例如，2004年底评出的全球超级计算机TOP100中排名首位的IBM BlueGene/L就采用网络；而另一家通信设备制造商，Avici公司在其推出的世界上第一台太比特路由器中也采用网络作为其交换网络拓扑。

图嵌入是将一个客图映射到一个主图中的一项技术，是评价一个网络性能的重要指标。 因此，对采用结构的多处理器系统进行嵌入研究是非常必要的。许多应用如结构仿真和处理器分配都可以用图嵌入来建模。在并行处理系统中，由于路和圈的结构均被用于模拟线性数组，所以在图嵌入问题中经常会选择路和圈来作为客图[6]。图的容错性是指当网络中出现故障时，该网络仍然具有的一些好的性质。二维网络是二维网络的扩展，它比网络具有更好的性能，近十几年来人们对网络的容错嵌入进行了大量的研究。Jung-Heum Park等人[7]证明了故障边数为1时，Torus(m,n)是哈密尔顿的，其中m≥2，偶数n≥4.Hee-Chul Kim等人[8]证明了故障元素的个数为2时，Torus(m,n)是哈密尔顿的，其中m,n≥3，且n是奇数。Yonghong Xiang等人[9]证明了故障边数为3时，Torus(m,n)是哈密尔顿的，其中m,n≥3且每个顶点至少有2度。本文主要研究故障边数达到4，在一类条件假设下，二维网络的哈密尔顿圈嵌入问题。具体来讲，证明了在假设条件下，二维(偶数)在具有至多4条故障边时仍包含哈密尔顿圈。

(1)每个顶点的度至少是2；

(2)不存在具有两个度为2的不相邻的顶点的4圈。

2 预备知识

一个二维m×n的环面(记作Torus(m,n)，其中m,n≥3)是由mn个顶点构成，且每个顶点用vi,j来表示，其中1≤i≤m，1≤j≤n.两个顶点vi,j与vi′,j′相邻当且仅当i′=i，j′=j±1(模n)或j′=j,i′=1±1(模m).对于每个i，边(vi,1,vi,n)称为行环绕边；对于每个j，边(vi,j,vm,j)称为列环绕边。图1(a)为Torus(3,4).注意到Torus(m,n)是一个4正则图(每个顶点的度为4)，且连通度κ(G)=4.将Torus(m,n)的所有列环绕边删去所生成的图记作Row-Torus(m,n).图1(b)为Row-Torus(3,4)，它是一个3连通的偶图。

图1 Torus(3,4)和Row-Torus(3,4)Fig.1 Torus(3,4) and Row-Torus(3,4)

设G是Torus(m,n)或Row-Torus(m,n).E(G)代表G的边集。Row(a∶b)是由{vi,j∶a≤i≤b,1≤j≤n}生成的G的子图；Col(a∶b)是由{vi,j∶ 1≤i≤m,a≤j≤b}生成的G的子图。Row(a∶a)和col(a∶a)可以分别用Row(a)和Col(a)来表示。为方便，称所有Row(a)上的边为行边，所有Col(a)上的边为列边。设(vi,j,vi,j+1)为Row(i)上一条行边，其中1≤i≤m.若与这条行边相邻的两条列边(vi,j,vr,j)与(vi,j+1,vr,j+1)同时非故障，其中r=i-1或r=i+1，则称这条边是r-行扩展边。列扩展边类似定义。

当m和n都是偶数时，Torus(m,n)是偶图；如果n是偶数，Row-Torus(m,n)也是偶图。对偶图G中的一个顶点vi,j，若i+j是偶数，则称它是偶顶点，否则是奇顶点。一条路P=〈v0,v1,…,vt〉是使得任意两个连续的顶点都相邻的一条互不相同的顶点序列。经过图G所有顶点恰一次的路是Hamilton路。在一个偶图G中，若不同部中的任意两个顶点s与t，均存在一条从s到t的Hamilton路，则G是Hamiltonian-Laceable[10]。经过G的每个顶点恰一次的圈被称为图G的Hamilton圈。称一个包含Hamilton圈的图是Hamilton图。

大量的文献研究了Torus(m,n)和Row-Torus(m,n)的拓扑性质，得到了许多好的研究结果。本文中用到了以下的结论：

引理1[7]：设F是Row-Torus(m,n)的一个故障边集，其中m≥2，偶数n≥4.若|F|≤1，则Row-Torus(m,n)-F是Hamiltonian-laceable.

由上述定理，有下面的结论：

推论1：设F是Row-Torus(m,n)的一个故障边集，其中m≥2，偶数n≥4.若|F|≤1，则Row-Torus(m,n)-F是Hamiltonian.

引理2[7]：设F是Row-Torus(m,n)的一个故障边集，其中m≥3，偶数n≥6.若|F|=2且这2条故障边不同时与一个3度顶点关联，则Row-Torus(m,n)-F是Hamiltonian.

3 主要结果的证明

这一部分将证明：在满足条件(1)与(2)的前提下，Torus(k,k)是4边容错的Hamilton图，其中偶数k≥6.

令F是Torus(k,k)的故障边集，且|F|≤4.为了方便，用Fr(Fc)表示所有故障行(列)边集合。不妨设|Fr|≥|Fc|，则|Fr|≥2.对于每个j∈{1,2,…,k}，记Cj=Col(j)，记Ej,j+1为Cj与Cj+1之间的行边集合，即Ej,j+1={(vi,j,vi,j+1)|i∈{1,2,…,k}}，其中j+1模k.

定理1：如果存在一个j′∈{1,2,…,k}，使得|Ej′,j′+1∩F|≥2，那么Torus(k,k)-F是Hamiltonian.

证明：由于|Ej′,j′+1∩F|≥2且|F|≤4，所以Torus(k,k)-Ej′,j′+1中至多有2条故障边。注意到Torus(k,k)-Ej′,j′+1与Row-Torus(k,k)同构。如果Torus(k,k)-Ej′,j′+1至多有1条故障边，或者有2条故障边但不同时与一个3度顶点关联，则分别由推论1与引理2知Torus(k,k)-Ej′,j′+1-F中存在Hamilton圈，故Torus(k,k)-F是Hamiltonian.

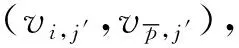
情况1另1条故障边是(vi,j′-1,vi,j′).

由于条件(1)成立且Torus(k,k)-Ej′,j′+1中至多有2条故障边，所以边(vi,j′,vi,j′+1)与边(vp,j′-1,vp,j′)非故障。又Torus(k,k)-Cj′与Row-Torus(k-1,k)是同构的，由引理1得，Torus(k,k)-Cj′中存在一条从vp,j′-1到vi,j′+1的Hamilton路P0.令P1=Cj′-(vi,j′,vp,j′).连接P0与P1，如图2(a)所示，得到Torus(k,k)-F中的一个Hamilton圈。

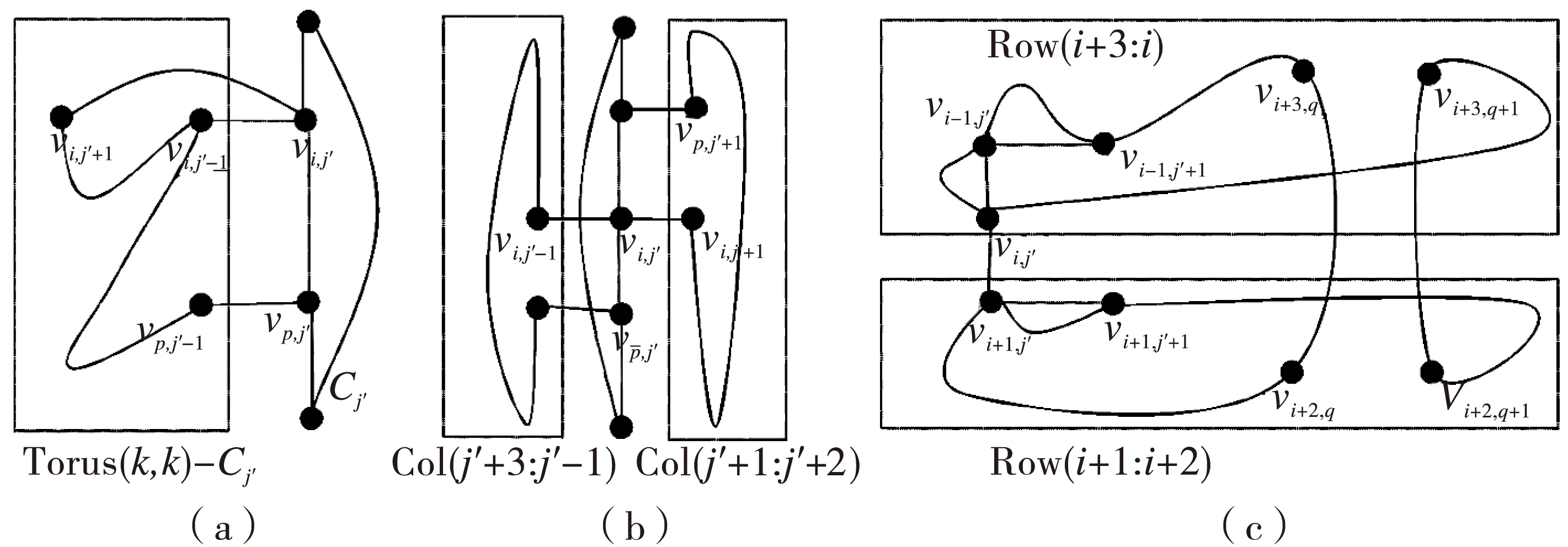
下面考虑对于任意的j∈{1,2,…,k}，当|Ej,j+1∩F|≤1时，Torus(k,k)-F仍然是Hamiltonian.首先讨论一种特殊的情况：

定理2：如果存在一个j′∈{1,2,…,k}，使得Cj′中存在1条故障边与2条故障行边相邻，那么Torus(k,k)-F是Hamiltonian.

证明：令e0=(vp,j′,vp+1,j′)是Cj′中满足上面条件的故障边，其中p∈{1,2,…,k}，则与e0相邻的2条故障行边的集合是W0={(vp,j′-1,vp,j′),(vp+1,j′,vp+1,j′+1)}或者是W1={(vp,j′,vp,j′+1),(vp+1,j′-1,vp+1,j′)}，不妨设前者成立。那么W1中的2条边均非故障。由于|Fr|≥2，所以Cj′中至多有2条故障列边。

如果Cj′中仅有1条故障边e0，令P0=Cj′-e0.注意到Torus(k,k)-Cj′与Row-Torus(k-1,k)同构，由引理1得，Torus(k,k)-Cj′-F中存在一条从vp+1,j′-1到vp,j′+1的Hamilton路P1.连接P0与P1，如图3(a)所示，得到Torus(k,k)-F中的一个Hamilton圈。

如果Cj′中有2条故障边e0，e1，则e1一定不与e0相邻。考虑Torus(k,k)中Row(p-1∶p+1)与Row(p+2∶p-2)两部分。注意到Row(p-1∶p+1)与Row-Torus(3,k)同构，且至多有3条故障边。令F′={(vp,j′-1,vp,j′),(vp,j′,vp+1,j′)}，由引理2得，Row(p-1∶p+1)-F′中存在经过边(vp+1,j′,vp+1,j′+1)的Hamilton圈C0，令P2=C0-(vp+1,j′,vp+1,j′+1)，又Row(p+2∶p-2)与Row-Torus(k-3,k)同构，由引理得，Row(p+2∶p-2)-F中有一条从vp+2,j′到vp+2,j′+1的Hamilton路P3.连接P2与P3，如图3(b)所示，得到Torus(k,k)-F中的一个Hamilton圈。

定理3：如果存在一个j′∈{1,2,…,k}，使得Cj′中有且仅有2条故障边，那么Torus(k,k)-F是Hamiltonian.

证明：令边(vp,j′,vp+1,j′)与(vq,j′,vq+1,j′)是Cj′中的2条故障列边，其中p,q∈{1,2,…,k}，p≠q，则另2条故障边为行边。需考虑Cj′中的任意1条故障边至多与1条故障行边相邻，则W0={(vp,j′,vp,j′+1),(vp+1,j′,vp+1,j′+1),(vq,j′,vq,j′-1),(vq+1,j′,vq+1,j′-1)}或W1={(vp,j′,vp,j′-1),(vp+1,j′,vp+1,j′-1),(vq,j′,vq,j′+1),(vq+1,j′,vq+1,j′+1)}是非故障边集，不妨设W0是非故障边集。令P0=Cj′-(vp,j′,vp+1,j′)-(vq,j′,vq+1,j′).

选择一个整数p*如下：如果(Ej′,j′+1∪Ej′-1,j′)∩F≠φ，令P*=j′+1；否则令P*是沿j′+1,j′+2,…,k,1,2,…,j′-2的顺序，第一个满足Ep*,p*+1∩F≠φ的整数。由定理1，设|Ep*,p*+1∩F|=1.由P*的选取知，Torus(k,k)-Cj′-Ep*+1,p*+2中Col(j′+1∶p*+1)与Col(p*+2∶j′-1)都至多包含1条故障边。注意到Col(j′+1∶p*+1)与Row-Torus(|p-j′|+1∶k)同构且|p-j′|+1≥2，由引理1知，Col(j′+1∶p*+1)-F中存在一条从vp,j′+1到vp+1,j′+1的Hamilton路P1.当Col(p*+2∶j′-1)仅有1列，即p*+2=j′-1时，Cj′-1-(vq,j′-1,vq+1,j′-1)是一条从点vq,j′-1到vq+1,j′-1的Hamilton路P2.当Col(p*+2∶j′-1)至少有2列时，同理Col(p*+2,j′-1)-F中存在一条从点vq,j′-1到点vq+1,j′-1的Hamilton路P2.连接P0，P1和P2，如图4所示，得到Torus(k,k)-F中的一个Hamilton圈。

定理4：如果存在一个j′∈{1,2,…,k}，使得Cj′中存在1条故障的非(j′-1)-列扩展边，Cj′+1中存在1条故障的非(j′+2)-列扩展边，那么Torus(k,k)-F是Hamiltonian.

证明：不妨设e0=(v1,j′,v2,j′)是Cj′中1条故障的非(j′-1)-列扩展边，e1=(vp,j′+1,vp+1,j′+1)是Cj′+1中1条故障的非(j′+2)-列扩展边，其中1≤p≤k/2.显然边(v1,j′-1,v1,j′)与(v2,j′-1,v2,j′)中仅有1条故障边，边(vp,j′+1,vp,j′+2)与(vp+1,j′+1,vp+1,j′+2)中也仅有1条故障边.注意到Torus(k,k)-Cj′-Cj′+1与Row-Torus(k-2,k)同构，由引理1知，Torus(k,k)-Cj′-Cj′+1是Hamiltonian-laceable.

如果p=1，令P0=Cj′-e0，P1=Cj′+1-e1，连接P0与P1得到Col(j′∶j′+1)-F的Hamilton圈C0.由|Ej′,j′+1∩F|≤1且k≥6，则Cj′中存在一条(j′-1)-列扩展边(vq,j′,vq+1,j′)，其中q∈{2,3,…,k}.令P2=C0-(vq,j′,vq+1,j′).显然，Torus(k,k)-Cj′-Cj′+1中存在一条从vq,j′-1到vq+1,j′-1的Hamilton路P3.连接P2与P3，得到Torus(k,k)-F中的一个Hamilton圈。

图3 定理2的示意图Fig.3 An illustration for Theorem 2

图4 定理3的示意图Fig.4 An illustration for Theorem 3

下设p≠1，根据2条故障行边的位置，对以下3种情况进行讨论：

情况1(vp+1,j′+1,vp+1,j′+2)或(v1,j′-1,v1,j′)是故障边。

由对称性，不妨设(vp+1,j′+1,vp+1,j′+2)是故障边，则边(vp,j′+1,vp,j′+2)非故障。由于2≤p≤k/2且偶数k≥6，则p+2≤k/2+2且vp+2,j′≠v1,j′.那么(vp+2,j′-1,vp+2,j′)是非故障边。Torus(k,k)-Cj′-Cj′+1中存在一条从vp,j′+2到vp+2,j′-1的Hamilton路P4.如图5(a)所示，在Col(j′∶j′+1)-F中找到一条从vp+2,j′到vp,j′+1的Hamilton路P5，连接P4和P5，构造了Torus(k,k)-F的一个Hamilton圈。

情况2(vp,j′+1,vp,j′+2)与(v2,j′-1,v2,j′)是故障边。

当p=2时，全部故障边都确定，如图5(b)所示，边(v1,j′-1,v1,j′)与(v3,j′+1,v3,j′+2)是非故障的。Torus(k,k)-Cj′-Cj′+1中存在一条从v1,j′-1到v3,j′+2的Hamilton路P4.令P5=Cj′-e0，P6=Cj′+1-e1.那么〈v1,j′-1,v1,j′,P5,v2,j′,v2,j′+1,P6，v3,j′+1,v3,j′+2,P4,v1,j′-1〉为Torus(k,k)-F的一个Hamilton圈。

由条件(2)知，p≠3.当p≥4时，(v1,j′-1,v1,j′)与(v3,j′+1,v3,j′+2)均是非故障边。Torus(k,k)-Cj′-Cj′+1中存在一条从v1,j′-1到v3,j′+2的Hamilton路P4.注意到Cj′-e0-(vp,j′,vp+1,j′)是由从点v1,j′到点vp+1,j′的路P7与从点v2,j′到点vp,j′的路P8组成；Cj′+1-e1-(v2,j′+1,v3,j′+1)是由从点vp+1,j′+1到点v2,j′+1的路P6与从点vp,j′+1到点v3,j′+1的路P10组成。如图5(c)所示，构造Torus(k,k)-F的一个Hamilton圈：〈v1,j′-1,v1,j′,P7,vp+1,j′,vp+1,j′+1,P9,v2,j′+1,v2,j′,P8，vp,j′,vp,j′+1,P10,v3,j′+1,v3,j′+2,P4,v1,j′-1〉.

定理5：设F是Torus(k,k)的一个故障边集且|F|≤4，其中偶数k≥6，若条件(1)与条件(2)满足，则Torus(k,k)-F是Hamiltonian.

证明：只需证明|F|=4的情形即可，不失一般性设|Fr|≥|Fc|，则|Fr|≥2.由定理1，只需考虑|Ej,j+1∩F|≤1，其中1≤j≤k.令e0=(v1,1,v1,k)是Fr中的1条故障行边，另1条故障边为e1=(vi′,j′,vi′,j′+1)，其中i′∈{1,2,…,k}，j′∈{1,2,…,k-1}.Torus(k,k)-Ek,1-Ej′,j′+1中有2条故障边。注意Torus(k,k)-Ek,1-Ej′,j′+1中Col(1∶j′)与Row-Torus(j′∶k)同构；Col(j′+1∶k)与Row-Torus(k-j′∶k)同构。下面讨论两种情况：

情况1Col(1∶j′)与Col(j′+1∶k)中各有1条故障边。

首先假设Col(1∶j′)与Col(j′+1∶k)都至少包含2列。显然Cj′中存在一条(j′+1)-列扩展边(vp,j′,vp+1,j′)，其中p∈{1,2,…,k}.由引理1知，Col(1∶j′)-F中存在一条从vp,j′到vp+1,j′的Hamilton路P0；Col(j′+1∶k)中存在一条从vp,j′+1到vp+1,j′+1的Hamilton路P1.连接P0与P1，得到Torus(k,k)-F的一个Hamilton圈。

其次假设Col(1∶j′)与Col(j′+1∶k)中的一个仅包含1列，不失一般性设Col(1∶j′)仅包含1列，即j′=1且Col(1∶j′)=C1.令Col(1∶j′)中的故障边e2=(vq,1,vq+1,1)，其中q∈{1,2,…,k}.如果e2同时与2条故障行边e0，e1相邻，由定理2知结论成立。如果e2至多与{e0,e1}中的1条故障边相邻，则e2是2-列扩展边或是k-列扩展边，不妨设e2是2-列扩展边。令P2[vq,1,vq+1,1]=C1-(vq,1,vq+1,1).由引理1知，Col(2∶k)-F中存在一条从vq,2到vq+1,2的Hamilton路P3.连接P2与P3，得到Torus(k,k)-F中的一个Hamilton圈。

图5 定理4的情况1与情况2Fig.5 Cases of Theorem 4.(a) Case 1;(b)and(c) Case 2

情况2Col(1∶j′)与Col(j′+1∶k)中，有一个包含2条故障边。

不失一般性，设Col(1∶j′)中有2条故障边，Col(j′+1∶k)中无故障。如果Col(1∶j′)仅有1列，这种情况在定理3中讨论过。下面设Col(1∶j′)中至少包含2列：

情况2.1Col(1∶j′)中至少包含3列。

若Col(1∶j′)中的2条故障边不同时与一个3度顶点关联，由引理2知，Col(1∶j′)-F中存在一条Hamilton圈C.注意到C至少经过Cj′中的3条边，则选择C∩Cj′中的一条(j′+1)-列扩展边(vp,j′,vp+1,j′)，其中p∈{1,2,…,k}.令P0=C-(vp,j′,vp+1,j′).显然Col(j′+1∶k)中存在一条连接vp,j′+1与vp+1,j′+1的Hamilton路P1.将P0与P1连接，构造了Torus(k,k)-F的一个Hamilton圈。

如果Col(1∶j′)中的2条故障边同时与一个3度顶点关联，不妨设它是点vq,j′，其中q∈{1,2,…,k}.由定理2与定理3，只需考虑Cj′中仅有1条故障边，且这条故障边不与e1相邻的情况，设Cj′中的故障边为(vq,j′,vq+1,j′)，显然(vq,j′,vq+1,j′)是(j′+1)-列扩展边。令F′=F∩E(Col(1∶j′))-(vq,j′,vq+1,j′)，则|F′|=1.由引理1知，Col(1∶j′)-F′中存在一条从vq,j′到vq+1,j′的Hamilton路P2.又Col(j′+1∶k)中存在一条连接vq,j′+1与vq+1,j′+1的Hamilton路P3.连接P2与P3，构造Torus(k,k)-F的一个Hamilton圈。

情况2.2Col(1∶j′)仅包含2列，即j′=2.

显然，Col(1∶ 2)中至少有1条故障列边。如果C1中存在1条故障的k-列扩展边，或者C2中存在1条故障的3-列扩展边，则构造Hamilton圈的方法如情况2.1第二自然段。

如果Col(1∶ 2)中的2条故障边都是列边，由定理3与4知结论成立。下面考虑1条故障边是行边(即E1,2中的边)的情况。不失一般性，设Col(1∶ 2)中的故障列边在C2中。Torus(k,k)中的4条故障边为：e0=(v1,1,v1,k)，e1∈E2,3，e2∈E1,2，e3∈E(C2).重新划分Torus(k,k)，即Torus(k,k)-E1,2-E2,3由子图C2与Col(3∶ 1)两部分组成，而且C2和Col(3∶ 1)中各包含1条故障边，同情况1一致。

综上所述，Torus(k,k)-F是Hamiltonian.

参考文献：

[1] ZHU X，HUANG Z，ZHANG J，et al.Granular computing based intrusion detection model upon network monitor data streams[C]∥Pervasive Computing and Applications，Nanjing.2007：414-418.

[2] LI W.Using genetic algorithm for network intrusion detection[C]∥Proceedings of the United States Department of Energy Cyber Security Group，Mississippi State.2004：1-8.

[3] FARAOUN K M，BOUKELIF A.Neural networks learning improvement using the K-means clustering algorithm to detect network intrusions[J].International Journal of Computational Intelligence，2006，3(2)：161-168.

[4] LEE S C，HEINBUCH D V.Training a neural-network based intrusion detector to recognize novel attacks[J].IEEE Transactions on Systems，Man and Cybernetics，2001，31(4)：294-299.

[5] OH S H，KANG J S，BYUN Y C，et al.Intrusion detection based on clustering a data stream[C]∥Software Engineering Research，Management and Applications，South Korea.2005：220-227.

[6] 马雪，原军，张宪敏.容错元立方体的边泛圈性[J].太原科技大学学报，2013，34(5)：398-400.

[7] PARK J H，KIM H C.Fault-hamiltonicity of product graph of path and cycle[M].Computing and Combinatorics.Springer Berlin Heidelberg，2003.

[8] KIM H C，PARK J H.Fault hamiltonicity of two-dimensional torus networks[C]∥Proc of Workshop on Algorithms and Cmputation WAAC'00，Tokyo.2000：110-117.

[9] XIANG Y，STEWART I A.Bipancyclicity in k-ary n-cube with faulty edges under a conditional fault assumpition[J].IEEE.Transactions on Parallel and Distributed Systems，2011，22(9)：1506-1513.

[10] 王世英，李晶，杨玉星.互连网络的容错嵌入[M].北京：科学出版社，2012.