圆环形活塞声源的辐射阻抗

曹 辉，张吉伟，白钧元

(陕西师范大学陕西省超声重点实验室，陕西西安 710100)

超声聚焦技术在超声诊断、超声探伤以及超声检测中的应用已受到人们的广泛关注[1]。在超声聚焦技术中，若沿着一条直线实现点的聚焦，就可以采用由同心圆环形活塞声源构成的聚焦阵，因此对同心圆环形活塞声源的辐射声场特性的研究就不可避免。在一个声学振动系统中，对声源辐射声场的研究主要有辐射声压指向特性和辐射阻抗特性两方面的内容。对于圆环形活塞辐射声源来说，文献[2－3]已经对其声场的指向特性做了详细的研究。另外，辐射阻抗是评价一个振动系统声学特性的重要参量，常被用来评价声学系统对外界的辐射声功率和估计声源的同振质量等[4]，因此研究同心圆环形活塞声源的辐射阻抗在实际中具有重要意义。

本文以同心圆环形活塞声源为研究对象，根据同心圆环形活塞声源表面的几何关系，利用微元法计算出了一定尺寸圆环形活塞声源振动时的辐射阻抗的理论值。并分析了在ω＜8.5kHz范围内活塞声源的各参量与圆环形活塞声源的辐射阻抗之间的关系，得出了一定尺寸同心圆环形活塞声源的同振质量和平均辐射声功率。为进一步研究圆环形活塞声源聚焦技术奠定了理论基础。

1 辐射阻抗

如图1所示，同心圆环形活塞声源的内径为a，外径为b，圆心都为o。圆环形活塞声源振动时会向周围的媒质辐射声波，从而在周围的媒质中就会产生辐射声场。由于圆环形活塞声源本身也处于自身所辐射的声场之中，所以圆环形活塞声源本身就必然受到辐射声场的反作用。圆环形活塞声源振动时，表面附近各处的声压是不均匀的，因此活塞表面各处所受到辐射声场的作用也不相等。根据辐射阻抗的定义

可知，只需求得辐射声场的反作用力就可计算出圆环形活塞声源的辐射阻抗的大小。式(1)中Zr为辐射阻抗，F为辐射声场的反作用力，u=uaejωt为振元的振速。将圆环形活塞表面分割成无限多个小面元，如图1所示。

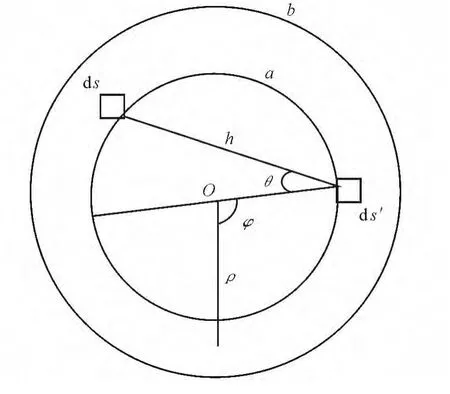
图1 圆环形活塞积分示意图Fig.1 The integral schematic diagram of ring piston

设面元ds的振动在面元ds'附近的媒质中产生的声压为dp。若面元ds与面元ds'之间的距离为h，则声压

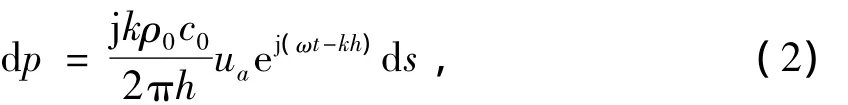
式中:k为波数，ρ0为媒质密度，c0为声波在媒质中的传播速度，ω为角频率。

根据式(2)可知，圆环形活塞上所有面元在ds'附近产生的总声压为

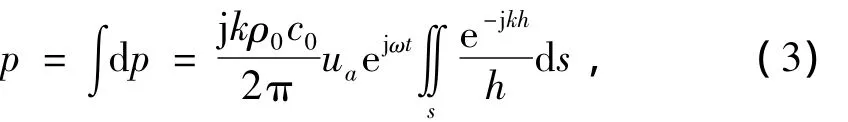
因此面元ds'受到辐射声场的反作用力f为

dF=－pds'， (4)式(4)中的负号表示dF的方向与ds'的运动方向相反。将式(3)代入式(4)，并对ds'积分，得到整个圆环形活塞表面受到自身辐射声场的反作用力为

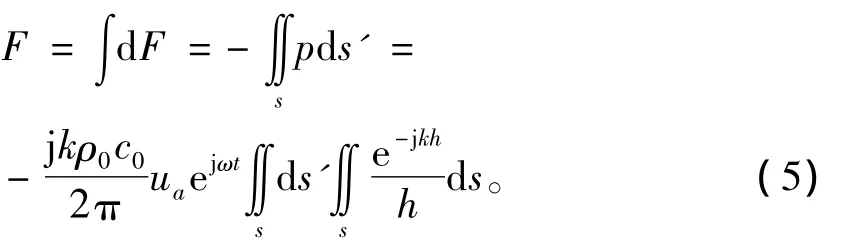
根据式(5)分析可知，活塞上每一对面元(面元ds与面元ds')的相互作用力会出现两次:一次是由于ds'振动在ds上产生的力;一次是由于ds振动在ds'上产生的力。由于这两个力大小相等，所以我们只考虑这一对面元之间相互作用力中的一个，然后再乘以2即可。

如图1所示，h为面元ds与面元ds'之间的距离，ρ为圆环极径，θ为直线h与通过ds'的一条直径之间的夹角，φ为极径ρ和圆心o与面元ds'连线的夹角。根据以上几何关系可得如下关系:ds=hdhdθ，ds'= ρdρdφ。积分上下限为:≤ h≤2ρcosθ，a≤ρ≤b，0≤φ≤2π。由上述分析可知，对面元ds与面元ds'积分之后，再乘以2就可得到辐射声场的反作用力f为

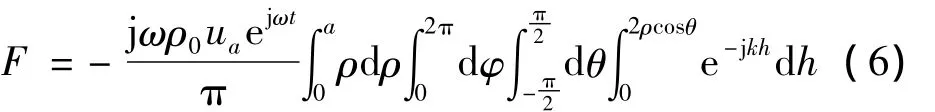
对上式(6)逐次积分可求得f的值为

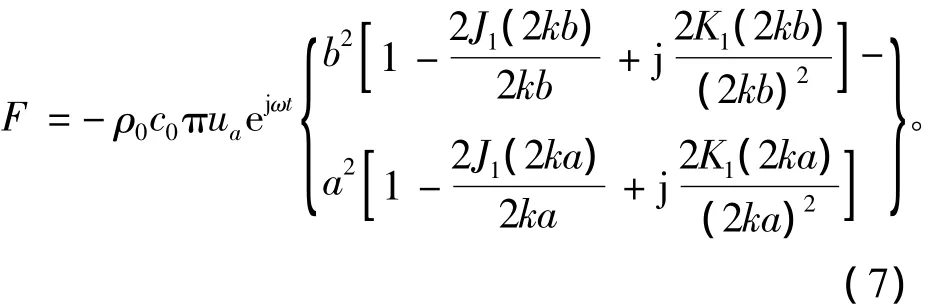
式(7)中，K1(x)是一阶修正贝塞尔函数，J1(x)是一阶柱贝塞尔函数。由于式(7)中包含贝塞尔函数，结果较为繁琐不便于分析，所以引入两个新函数

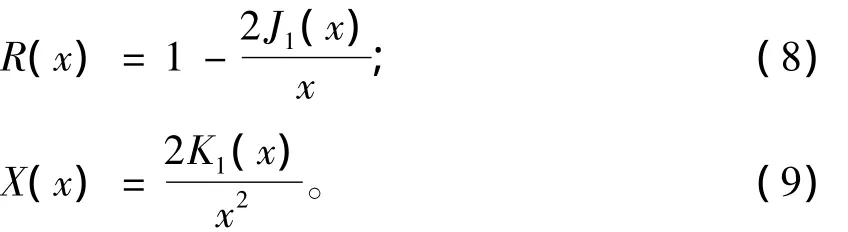
于是上式(7)可以简化为

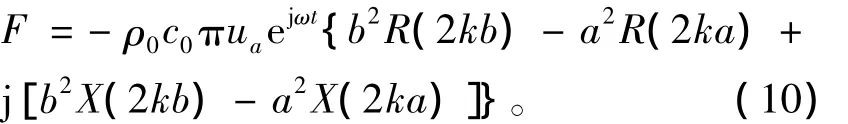
从上式(10)可以看出，声场的反作用力与活塞声源的振动频率、活塞声源的尺寸(包括活塞的内径尺寸、外径尺寸)密切相关。

对式(10)进一步简化，在ω ＜8.5kHz范围内，根据圆环形活塞声源的大小(内径 a=0.01m，外径b=0.02m)和函数R(x)、X(x)的性质，可得函数R(x)和X(x)的取值表达式为

因此，综合式(10)，(11)，可得圆环形活塞声源受到辐射声场的反作用力为

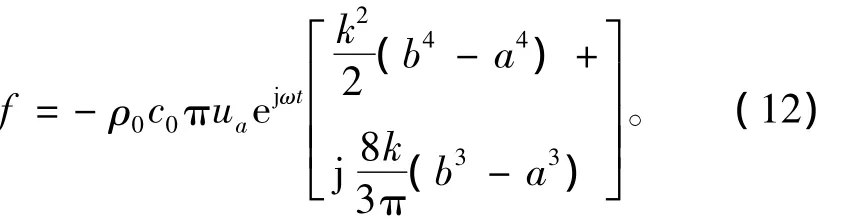
再根据式(1)中辐射阻抗的定义就可计算出圆环形活塞声源的辐射阻抗为

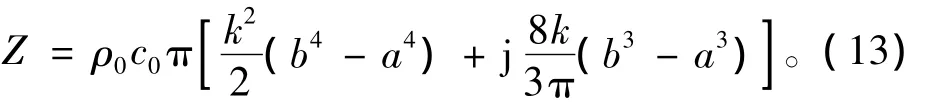
2 特性分析

由式(13)可知圆环形活塞声源系统的辐射阻抗由实部和虚部组成，分别称其为辐射阻Rr和辐射抗Xr，并将频率ω与波数k的关系ω=kc0代入式(13)就可以得到辐射阻和辐射抗表达式

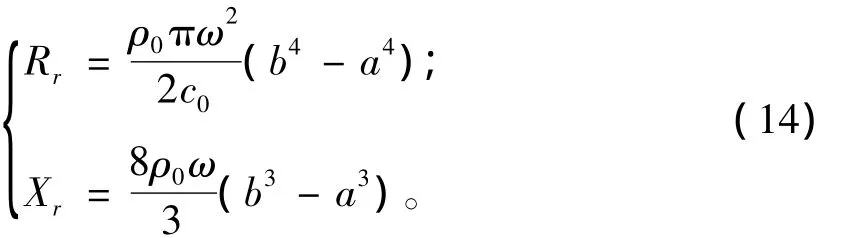
进一步可求得圆环形活塞声源的同振质量为

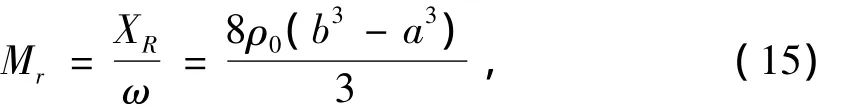
圆环形活塞声源的平均辐射声功率为

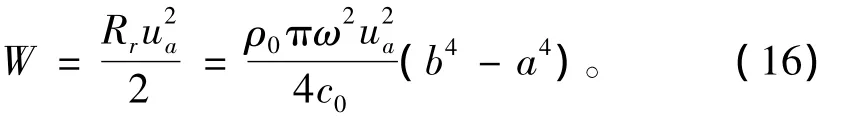
由式(13)和(14)分析可知，在媒质条件一定时，圆环形活塞声源的辐射阻抗与活塞声源的尺寸和振动频率密切相关。

根据圆环形活塞声源的辐射阻抗的表达式(14)，若已知圆环形活塞声源的尺寸a=0.01m，b=0.02m，则圆环形活塞声源的辐射阻抗与振源频率ω之间的关系如图2所示。

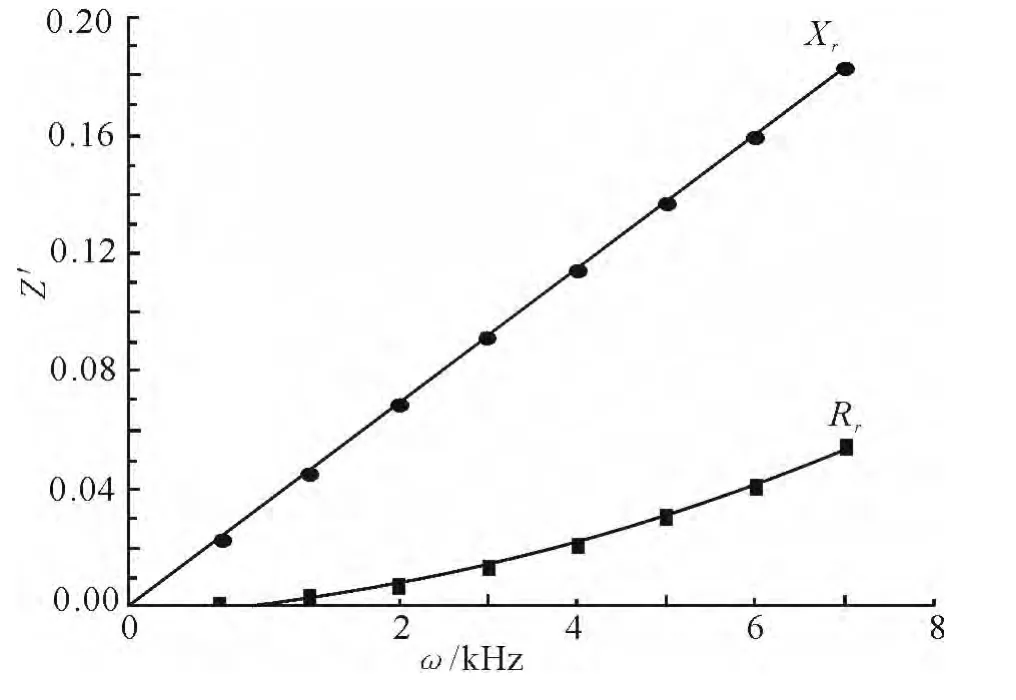
图2 圆环形活塞的辐射阻抗与振源频率之间的关系Fig.2 The relationship between radiation impedance from ring piston and frequency of vibration source

若已知圆环形活塞声源的内径a=0.01m和圆环形活塞声源的振动频率ω=3.4kHz(经计算在其他ω＜8.5kHz的时频率也有相似规律)，则圆环形活塞声源的辐射阻抗与圆环形活塞声源的外径b之间的关系如图3所示。

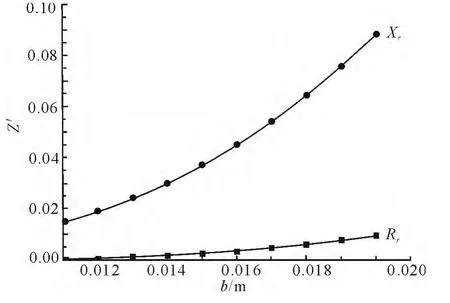
图3 圆环形活塞的辐射阻抗与声源外径b之间的关系Fig.3 The relationship between radiation impedance from ring piston and external radius b

若已知圆环形活塞声源的外径b=0.02m和圆环形活塞声源的振动频率ω=3.4kHz，则圆环形活塞声源的辐射阻抗与圆环形活塞声源的外径a之间的关系如图3所示。图1、图2、图3中Z'表示圆环形活塞声源的辐射阻抗的相对值。

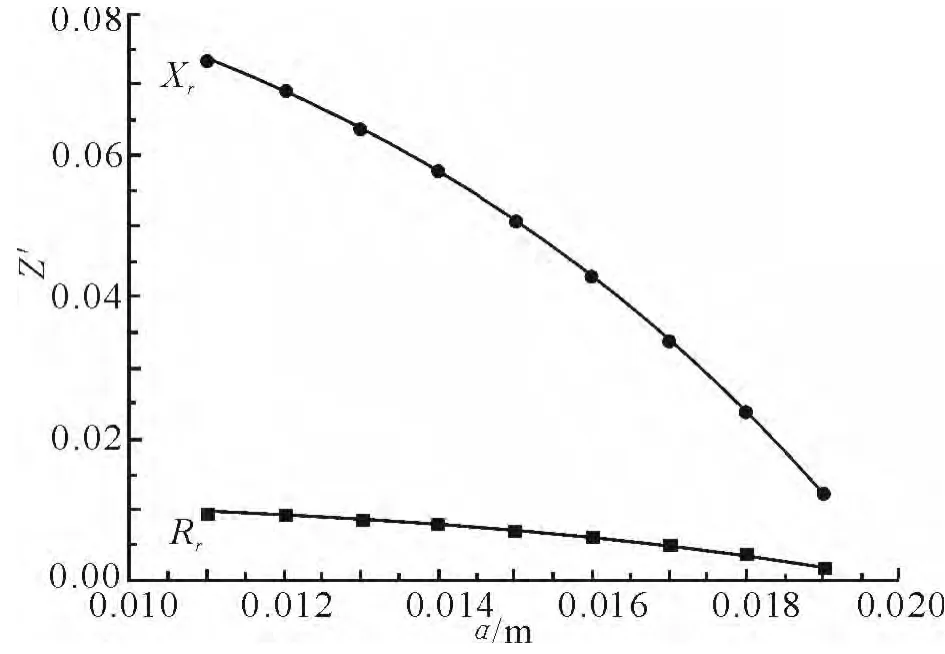
图4 圆环形活塞的辐射阻抗与声源内径a之间的关系Fig.4 The relationship between radiation impedance from ring piston and insiade radius a

从而进一步分析，当圆环形活塞声源的大小一定时，其辐射阻抗只与振源的振动频率有关，由图2可知:圆环形活塞声源的辐射阻和辐射抗都随着振源频率的增大而增大，其中辐射抗随振源频率的增加比辐射阻随频率的增加更快，说明圆环形活塞声源的辐射抗比辐射抗受频率的影响更大。当圆环形活塞声源的振动频率和内径一定时，由图3可知:圆环形活塞声源的辐射阻和辐射抗都随着活塞声源外径的增大而增大，并且辐射抗的值大于辐射阻的值。当圆环形活塞声源的振动频率和外径一定时，由图4可知:圆环形活塞声源的辐射阻和辐射抗都随着活塞声源内径的增大而减小，并且辐射阻的值小于辐射抗的值。综合图3和图4可看出，a或b的变化实际上就是圆环形活塞声源的环宽的变化，辐射阻抗随环宽的增大而增大，反之亦然。因此，圆环形活塞声源的环宽和振动频率是决定其辐射阻抗的关键参量。若假设圆环形活塞声源的内径a为0，则其变为半径为b的圆形活塞声源。经计算此时的圆形活塞的辐射阻为和辐射抗为与文献[4]中的结果相符。

3 结语

声源的辐射阻抗是评价一个振动系统声学特性的重要参量，研究同心圆环形活塞声源的辐射阻抗在实际中具有重要意义。本文以同心圆环形活塞声源为研究对象，在ω＜8.5kHz范围内，根据同心圆环形活塞声源表面的几何关系，利用微元法计算出了一定尺寸圆环形活塞声源振动时的辐射阻抗的理论值。并分析了影响圆环形活塞声源的辐射阻抗的因素，结果表明:圆环形活塞声源的辐射阻抗与声源的振动频率、活塞声源的外径和内径密切相关。辐射阻抗随着振动频率的增大而增大;随内径a的增大而减小;随外径b的增大而增大。并且辐射抗的值大于辐射阻的值，上述参量的变化对辐射抗的影响较大。最后得出了一定尺寸同心圆环形活塞声源的同振质量和平均辐射声功率。为进一步研究圆环形活塞声源聚焦技术奠定了理论基础。

[1]任惠娟，贺西平，胡新伟.方形活塞声源辐射的数值计算[J].陕西师范大学学报(自然科学版)，2006，34(3):52-55.

[2]李锦，任中杰，林书玉.环状活塞换能器辐射声场研究[J].陕西师范大学学报(自然科学版)，2003，31(4):28-31.

[3]任惠娟，贺西平，扈风.环状活塞声源辐射声场指向性研究[J].陕西师范大学学报(自然科学版)，2007，35(3):40-43.

[4]杜功焕，朱哲民，龚秀芬.声学基础[M].南京:南京大学出版社，2001.

[5]何琳，朱海潮，邱小军，等.声学理论与工程应用[M].北京:科学出版社，2006.

[6]马大猷.声学手册[M].北京:科学出版社，2004.

[7]何祚镛，赵玉芳.声学理论基础[M].北京:国防工业出版社，1981.

[8]高立民，曹辉.液体中光击穿所激发声场的研究[J].光子学报，2011，40(10):1586-1589.

[9]曹辉，尚志远.液体中光击穿所激发声场的方向性[J].西北大学学报(自然科学版)，2003，33(1):19-22.