基于偏心率向量含约束多圈Lambert问题

黄英志，泮斌峰，唐 硕

(西北工业大学航天学院，陕西西安 710072)

Lambert问题作为二体轨道的边值问题，通常定义为[1]:“二体问题中，给定两个终端位置向量和转移时间，求转移轨道”。作为天体力学中的经典问题，又由于其在空间技术应用方面和数学上的重要性，从高斯时期起，Lambert问题吸引了大量学者的关注，从而有多种求解方法被提出来。

Lambert问题最早的求解方法可追溯到高斯，他利用圆锥曲线的几何性质解决了此问题。Lancaster[2]第一次提出使用无量纲量 x=作为迭代变量数值求解Lambert问题，统一了椭圆、抛物线和双曲线全部转移轨道。Battin[3]沿用 Lancaster提出的积分变量，利用二点边值问题的不变量(Invariance)拓展改进了Gauss的方法，并弥补了Gauss方法在转移角为180°时的奇异问题。Sun[4]同样以 x为变量，详细研究了轨道转移时间的极值特性，给出了多圈Lambert问题中解与最大飞行圈数的关系。在以其他积分变量为基础的研究中，Nelson[5]使用航迹角γ为迭代变量对问题进行求解，然而他未能给出转移时间相对于γ的解析导数，只使用二分法进行搜索;Jaemyung[6]同样使用γ为迭代变量，但给出了解析导数信息，使得数值解算更加容易收敛。特别值得注意的工作来自 Avanzini[7]，他首次提出使用偏心率向量垂直于转移弦线的分量大小eT为迭代变量，建立了以其为变量的描述体系，并给出了转移时间相对于eT的解析导数，便捷而直观地解决了 Lambert问题;Quan He[8]将Avanzini的工作推广到了多圈Lambert问题。以上对Lambert问题的解均是从纯数学角度描述而并未考虑实际工程中的约束情况，Zhang[9]首次提出了将近地点与远地点的约束加入Lambert问题的求解中，从而从多解中筛选出满足工程约束的解。然而，Zhang 沿用 Prussing[10]的方法，使用轨道半长轴a为迭代变量。由于a并非转移时间的单值函数，故而使得约束函数的描述复杂且难以分析其分类讨论繁杂冗长。本文使用横向偏心率向量大小eT为积分变量，详细讨论了以其为变量的轨道参数特性，给出了约束函数的特性分析，求解了引入轨道约束的多圈Lambert问题。从求解过程可看出，与Zhang提出的方法相比，本文提出的方法解算次数更少，求解过程更为直接且讨论过程更为简捷。

1 横向偏心率向量描述方法

经典Lambert问题如图1所示，其中F表示重力场的中心，P1和P2为初始与终端位置，其分别对应以F为中心的终端向量r1和r2;Δθ表示两终端向量间的夹角，即转移角;c表示连接P1与P2两点的弦长，e为偏心律向量。

根据文献[1]的推导，当给定了Lambert问题的几何条件后，其偏心率向量e唯一决定了轨道的形状，并且在P1P2的投影是一定值。这也就是说，偏心率向量可以分解成为垂直于P1P2的“横向”可变分量eT和平行于P1P2的定常分量eF。这一性质使得我们可以使用偏心率向量的横向分量eT来唯一描述转移轨道的性质。

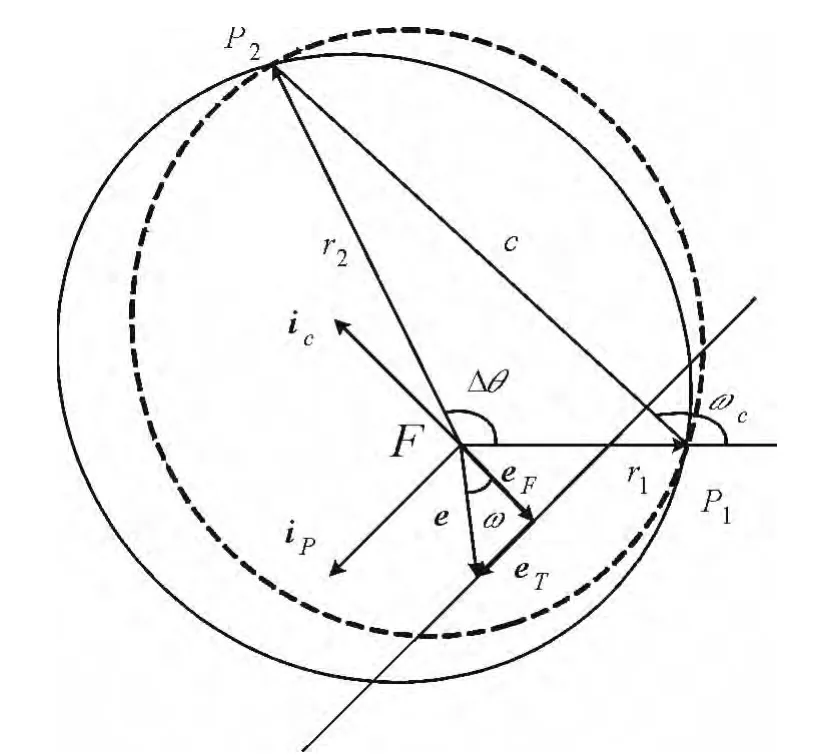
图1 Lambert问题的几何构型Fig.1 Geometry of the Lambert problem

纵向分量可表示为[1]:

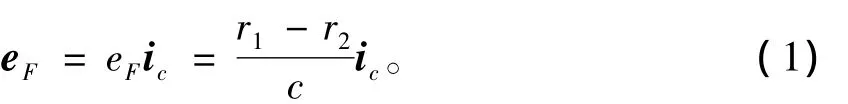
其中ic表示沿P1P2方向的单位向量。横向分量eT的大小用eT表示，定义与横向单位向量ip同向时为正，ip与P1P2垂直。横向分量eT与纵向分量eF的和即为偏心率向量:

从而偏心率的大小可写为

当横向分量eT等于零时，偏心率向量退化为eF且与弦线P1P2平行，此时的转移轨道为Battin所定义的Lambert问题中的基本椭圆(Fundamental Ellipse)，该椭圆的长半轴与弦线P1P2平行，如图1实线椭圆所示。基本椭圆的基本参数可以作为转移轨道参数的中间量，其偏心率、半长轴以及半通径由以下公式给出

式中角标F表示其为基本椭圆轨道下的量。

在基本椭圆轨道的基础上，我们以半通径为中间量建立一般转移轨道与基本椭圆的联系，从而以 eT为变量得到一般椭圆的参数。根据Avanzini[6]给出的公式有

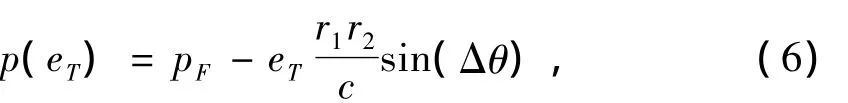
则由轨道力学基本关系可得轨道的半长轴为

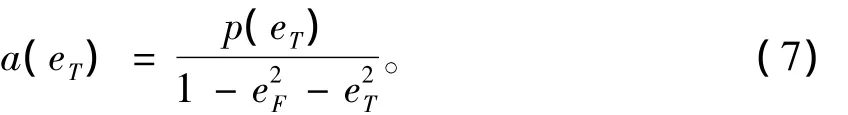
在轨道平面内定义r1及其垂线方向为参考直角坐标系两轴方向，ωc为ic与r1的夹角，则ic可表示为(cos ωc，sin ωc)T，ip可表示为(－ sin ωc，cos ωc)T，从而对一般转移轨道，其偏心率向量可表为

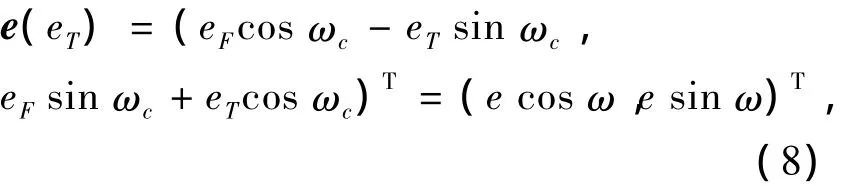
则e相对参考向量r1的角度ω可表为

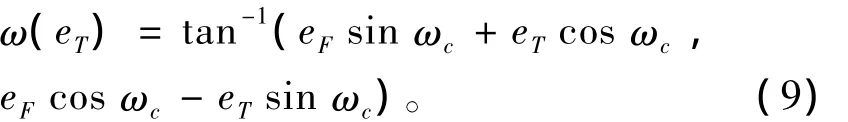
式中的tan－1(x，y)为四象限反正切函数。根据上式由几何关系可得到P1和P2两点的真近点角为

由偏近点角与真近点角的关系可得到终端点处的偏近点角为

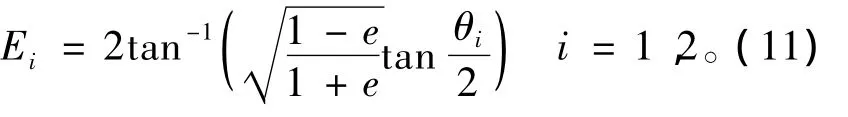
由式(1)－(11)可见，在给定了Lambert问题的几何参数r1，r2以及Δθ以后，转移轨道的基本参数如半长轴a，半通径p，终端点的真近点角θ1θ2以及偏近点角E1E2都可表为横向离心率eT的函数，从而建立了以eT为自变量的参数体系。Lambert问题的轨道转移时间是以上参数的函数，从而成为了eT的单值函数。轨道转移时间Δt可表示为[7]

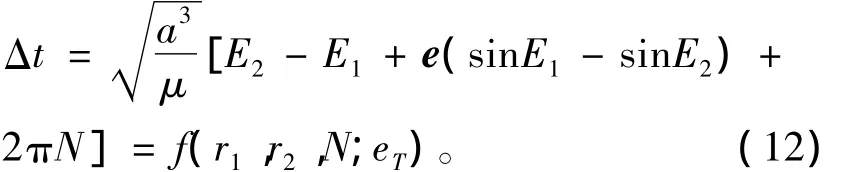
式中N为转移轨道的圈数。式(12)表明，当多圈Lambert问题几何参数r1和r2以及圈数N给定以后，转移时间Δt就成为了eT的函数，且由于函数曲线特性良好，最简单的牛顿迭代法就足以很快收敛到给定Δt的解。牛顿迭代法所需的导数信息可由式(12)对eT直接求导得到，Quan He[7]给出了该式导数求解过程，本文不再赘述。值得注意的是，对于多圈Lambert问题，我们只考虑椭圆轨道，故eT应限制在一定范围内。事实上，由于椭圆轨道偏心率满足0＜e＜1，于是结合式(3)有:

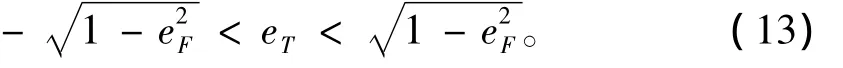
由于eF的取值范围被限制在(－1，1)内，故而数值迭代变得十分方便。图2给出了多圈Lambert问题转移时间Δt相对于eT的曲线，圈数N取0－5，其几何参数采用归一化参数，取r1=1，r2=2，Δθ=120°，μ =1。由图2 可见，Δt是 eT的单值函数，且其导数在eT上下界两点以外的地方皆为有界的。当N=0时，Δt随eT单调递增;当N ＞0时，同一Δt对应两个eT的解，Δt在eT的上下界处趋于无穷大，并存在一个导数为零的极小值。正如Prussing[10]得出的结论，在给定Δt以后，多圈Lambert问题一共有2Nmax+1个解，其中Nmax是最大允许的转移轨道圈数。

在得到以上公式及性质以后，即可数值求解出给定Δt值后的对应所有可能的解。

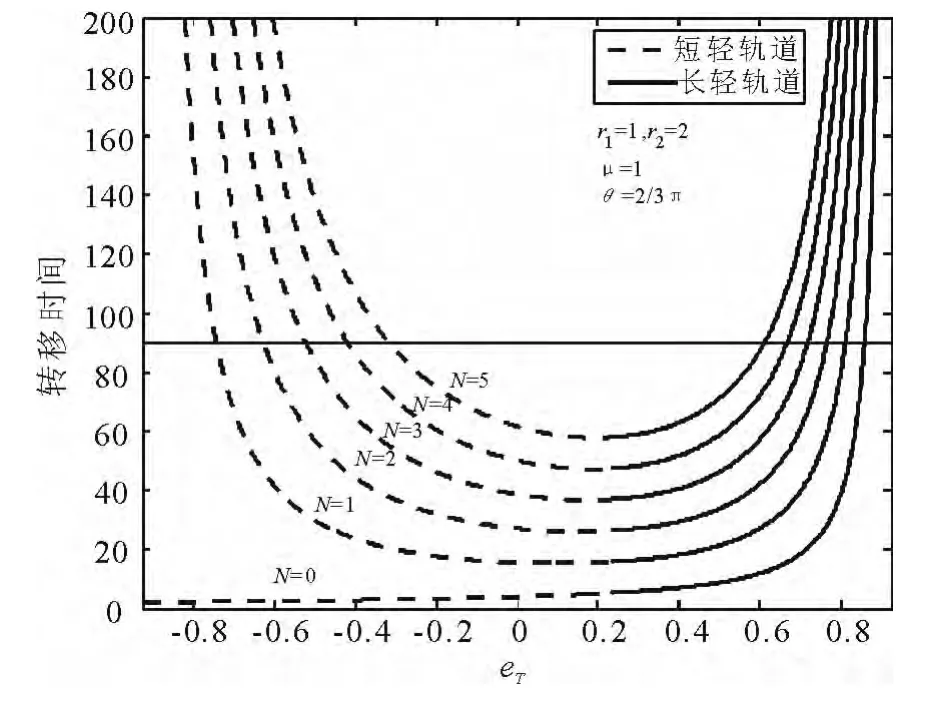
图2 归一条件下转移时间随eT的变化关系Fig.2 Transfer time as a function of eT

2 轨道性质与横向偏心率关系

在以半长轴a为自变量描述Lambert问题时，对同一轨道转移时间，有两个不同的a值的解，分别对应所谓的长径(long－path)和短径(short－path)轨道，造成了分析的困难。由于Lambert问题中轨道与eT是一一对应的，故而同一个eT有两个a值相对应。事实上，确定了轨道的半长轴以后，了解其属于长径轨道还是短径轨道对轨道分析具有重要意义，因此本节讨论半长轴与eT的关系。由式(6)和(7)知

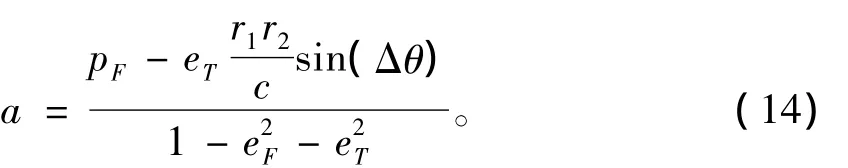
轨道长径与短径的分界点位于a对eT的导数为零的点，对(14)式求导有:

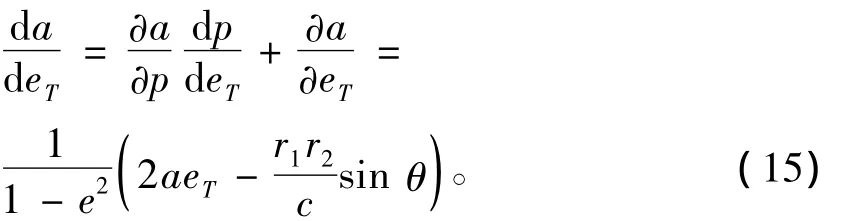
对于椭圆轨道有e＜1，故而极值点有

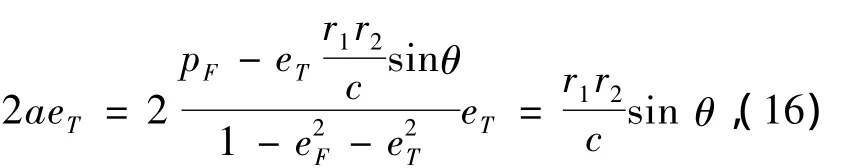
令

式(16)化简为

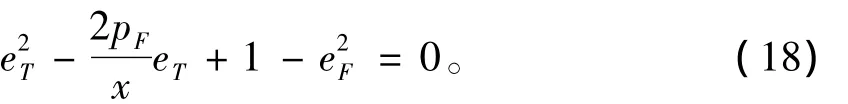
二次方程(18)的解为

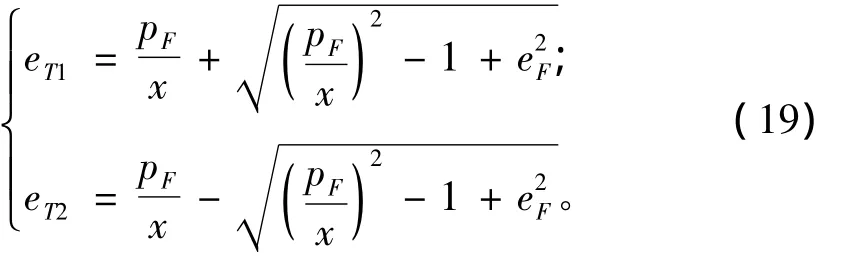
注意到eT须满足式(13)，故知其必处于(－1，1)内。对式(19)分析可知，当θ∈(0，π)时，eT1单调递增且趋于正无穷(由于为正且趋于零);θ∈ (π，2π)时，eT2单调递增且趋于正无穷，故其在对应的区间上都不满足式(13)的约束，如图3所示。由以上分析可知半长轴的极小值点为

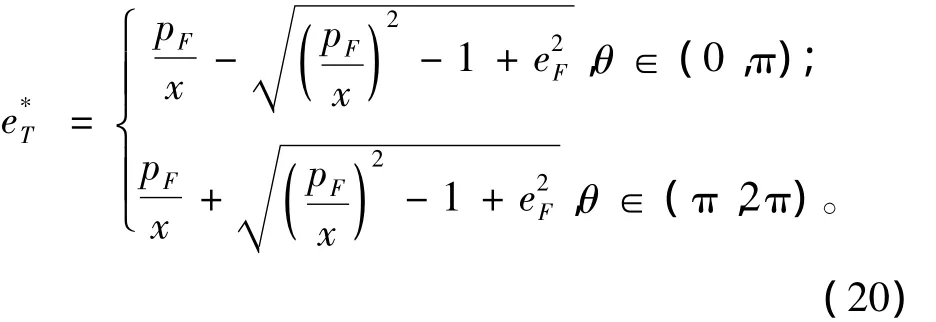
如图1所示，当eT为负时，e所指向的近地点位于转移弧线上，转移轨道属于短径，故当eT小于e*T时，转移轨道为短径，反之为长径。图4给出了 r1=1，r2=2，Δθ=120°时a与eT的关系，其中虚线表示短径，实线表示长径。由此关系分析图2，同样以虚实线表示了轨道的长径短径性质，可见其属性由式(20)决定，即e*T完全由Lambert问题的几何参数决定，故应注意在图2中长短径的分界点并不位于每条Δt－eT曲线的极值点，亦即同一N值Lambert问题的两个解并不一定分别对应长径和短径轨道。

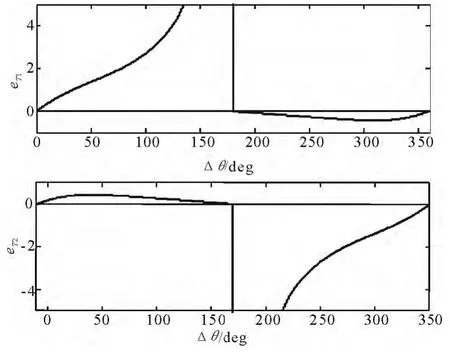
图3 长短径分界点与转移角的关系Fig.3 Locations of dividing point as a function of transfer angle

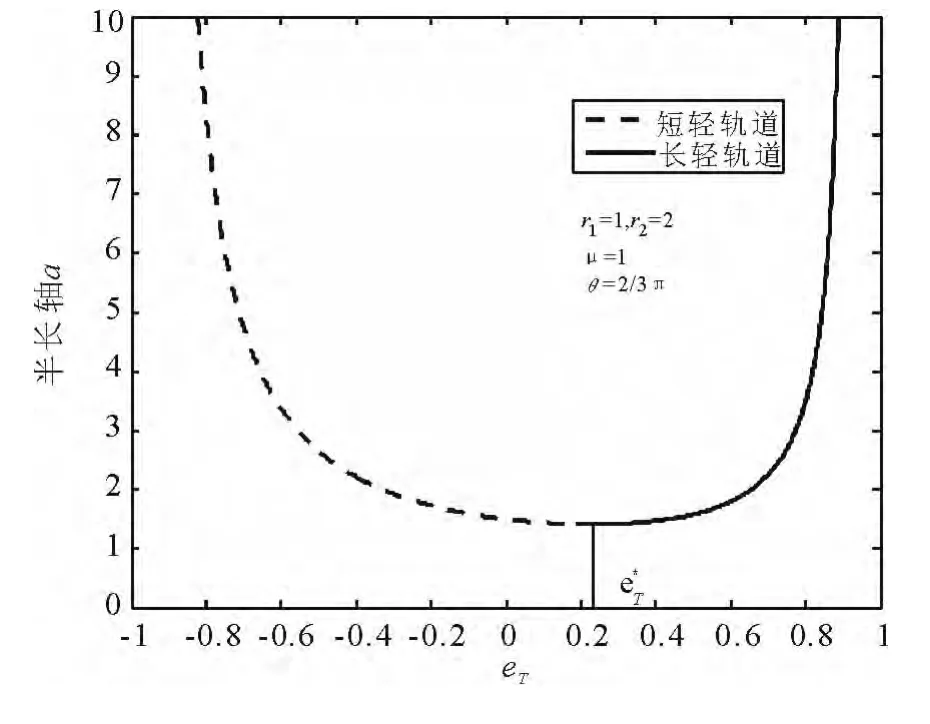
图4 轨道半长轴与eT的关系曲线Fig.4 Semimajor axis as a function of eT

在确定了e*T的值以后就可以很快地判断所求出的Lambert解究竟属于长径轨道还是短径轨道。

3 约束函数的特性分析

在采用以上方法可以求解出所有满足Δt条件的Lambert转移轨道并确定其轨道性质，然而这些轨道并不全都满足物理和工程上的约束。Zhang[8]提出了两种对轨道的约束:①轨道的近地点高度应大于某定值，以避免落入近地大气中;②轨道的远地点高度应小于某定值，以避免卫星可用观测时间过短。然而，Zhang在文中使用半长轴a为变量进行分析，a的非单值性使得对两种约束建立的函数无法精确分析，从而使得讨论变得十分复杂。下面的讨论使用eT为变量对两种约束进行分析，并极大简化讨论的过程。

为了使得轨道满足近地点及远地点的约束，要求以下不等式成立:

其中Rp表示近地点高度下限，Ra表示远地点高度的上限，其均为定值。由式(21)的约束条件，定义约束函数f函数和F函数，分别要求满足

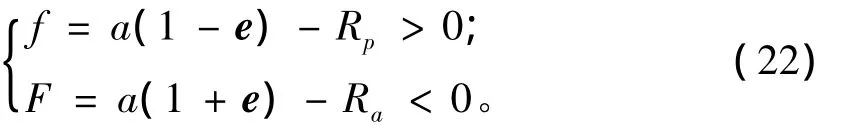
由式(22)的两个不等式限制可以进一步缩小eT的范围，从而减少迭代求解的次数，并排除不满足实际需求的轨道。通过观察f函数和F函数相对于eT的关系曲线形式，可见f函数随eT变化为先增后减，F函数则为先减后增，二者分别存在一个极大值及一个极小值点。如果能证明两个约束函数分别满足这样的增减关系，那么在式(22)限制下的eT取值范围将满足十分简洁的形式，即:

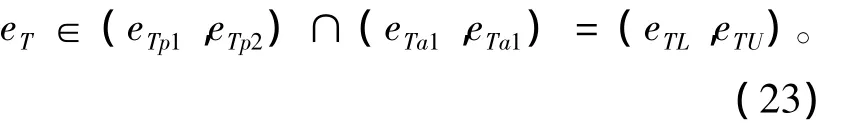
其中eTp1，eTp2及eTa1，eTa2分别是f－eT曲线和F －eT曲线与y=0的交点，分别位于各自极值点左右两边。下文先证明这两个约束函数在eT的范围(－1，1)内分别只有一个极值点，并确定极值点的位置;然后给出式(23)中eT范围的确定方法。

对于f函数，其极值点位于对eT导数为零处，对eT求导得:

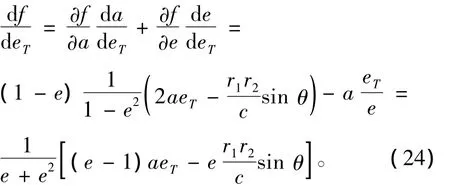
令式(24)左端为零，则有等式右端括号内为零:

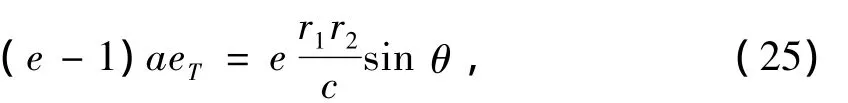
代入(3)，式(6)和(7)得

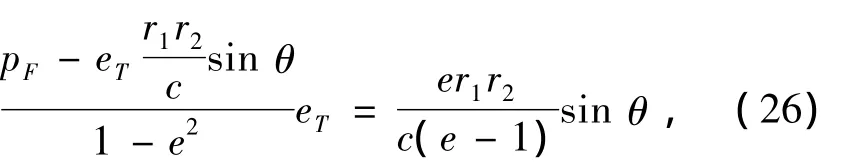
代入式(17)并整理得

同理，对于F函数，其对eT求导得

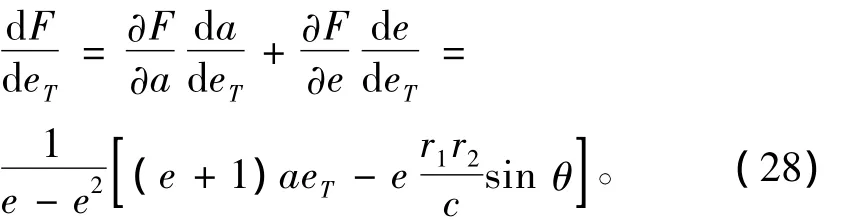
取式(28)右端括号内为零有:

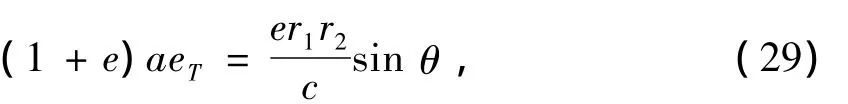
代入式(3)，(6)，(7)及式(17)并整理得到:

综合式(27)及式(30)，我们得到两种约束函数f函数和F函数的极值条件:

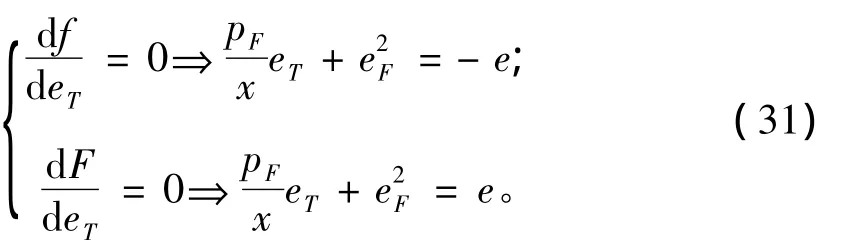
式(31)等效为

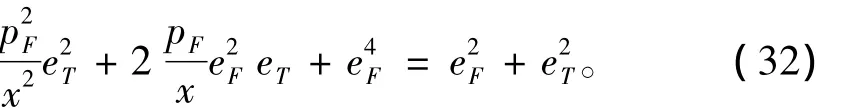
整理为关于eT的二次方程:

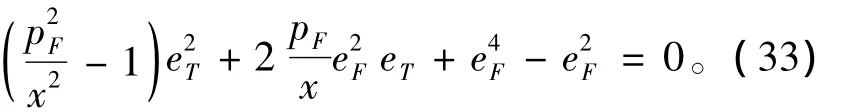
为了确定根的分布情况，取eTr1和eTr2分别表示式(34)右端取“+”号和“－”的根，定义辅助函数来判断所得根为哪个约束函数的极值，由式(31)可知，G=0时说明其为f函数的极值，G≠0时说明其为F函数的极值。图5表示r1=1，r2=2时，eTr1和eTr2随夹角Δθ变化的曲线以及对应的G函数值，其中实线表示方程的根值，虚线表示辅助函数G的值。

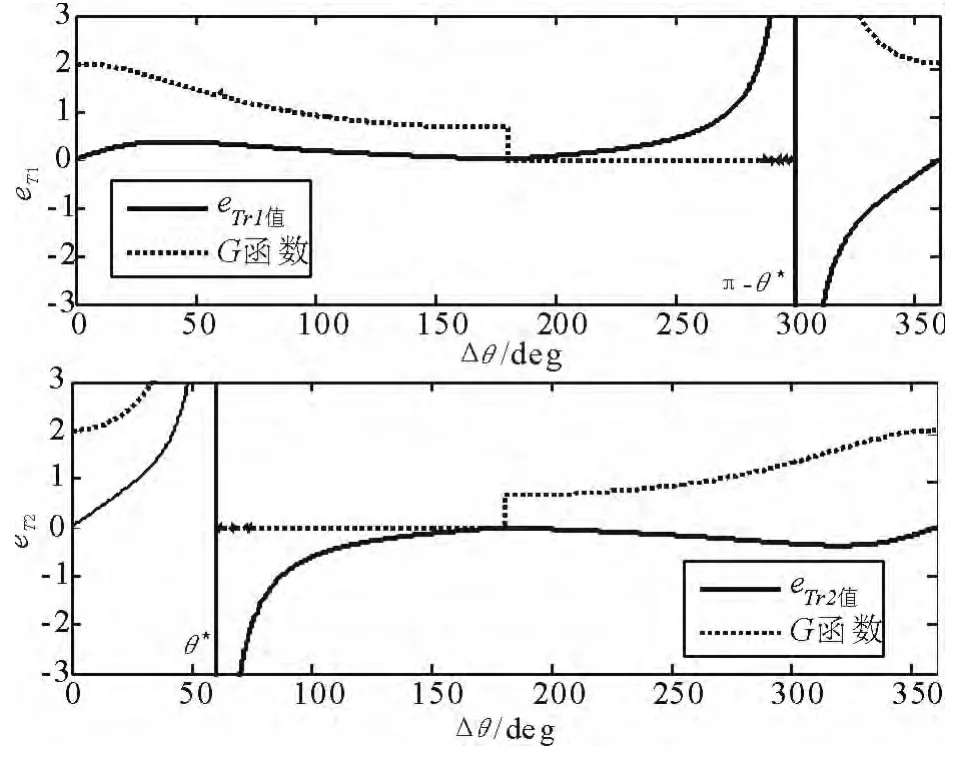
图5 约束函数极值点与转移角的关系曲线Fig.5 Extremum points of constrain functions as a function of transfer angle

对图5分析可见，当θ∈(0，π)时，对eTr1有0 ＜ G ＜ 2，故eTr1为f函数的极值;当θ∈(θ*，π)时，对eTr2有G=0，故eTr2为F函数的极值点;当θ∈(0，θ*)时，对eTr2有G ＞2，说明此根无效应舍去。其他区间的分析类似，方程根分布情况综合为表1所示。需注意的是θ*的值由式(34)右端的分母为零对应，即由解得。

表1 约束函数极值点分布Tab.1 Extremum points of constrain functions

综上可得，在区间eT∈(－1，1)上可能有一个根或没有根必有一个根，又由于f与F皆为连续函数，故其在讨论区间内最多只有一次增减性的变化，式(23)成立。

在确定了两约束函数的增减性质后，式(23)的求解本身并不困难。对于f函数，令f=0有

代入式(3)，(6)和(7)得:

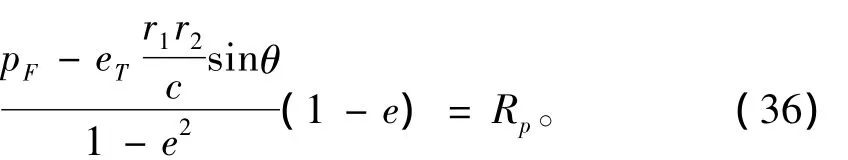
整理可得:

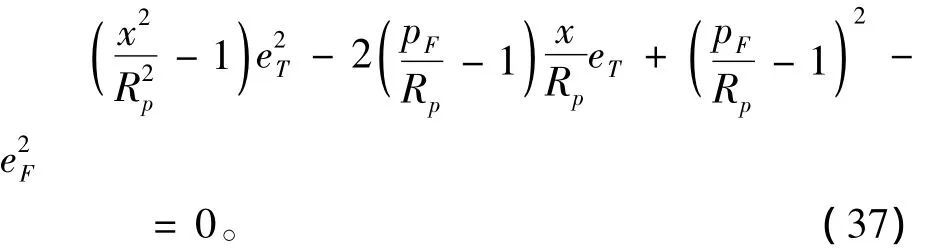
由式(37)可见f=0的解是一个一元二次方程的两个根，其解的分布情况符合以上对f函数增减性的分析。与上同理易求解出F=0的两个解，同样为一个二次方程的两个根。值得注意的是，式(37)只是f=0的必要条件而非充分条件，对于超出eT取值范围式(13)的根应去除而以相应范围边界代之。

将两种约束条件下eT的取值范围式(23)施加到式(12)的数值解算过程，即可得到满足实际约束条件的转移轨道。

4 解算过程

在确定了eT的范围后，首先可确定可行解轨道运行的圈数。在Lambert问题中给定转移时间后，转移圈数成为eT的函数，有:

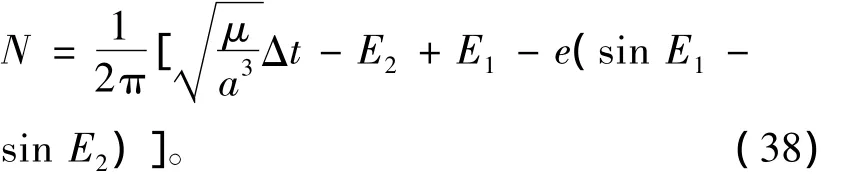
假设N(eT)在eTm处达到极大值，即

如图6所示，在式(23)的限制范围内，N－eT曲线与整数值的横轴交点即为可行解，则在给定Lambert问题所有数学解中，可行解的运行圈数N满足:

1)若eTm＞eTU，则

「N(eTL)⏋≤ N ≤⎿N(eTU)」;

2)若eTm＜eTL，则

「N(eTU)⏋≤ N ≤⎿N(eTL)」;

3)若eTL＜eTm＜eTU，则

N ∈ (min(「N(eTL)⏋，「N(eTU)⏋)，⎿Nmax」)。

应注意情况3)中相同的运行圈数N可能对应两条轨道。

在求得满足约束的可行圈数N之后，以求得的约束边界eTL和eTU为迭代初始变量，经迭代计算即可求出所有可行解。须注意的是，通过这种迭代策略，有可能迭代到约束边界以外的解，最极端的情况可能求出2n个解(n为可行解个数)，须用式(23)将边界外的解滤除。在实际的解算过程中，迭代通常会顺利收敛得到所求的n个解。

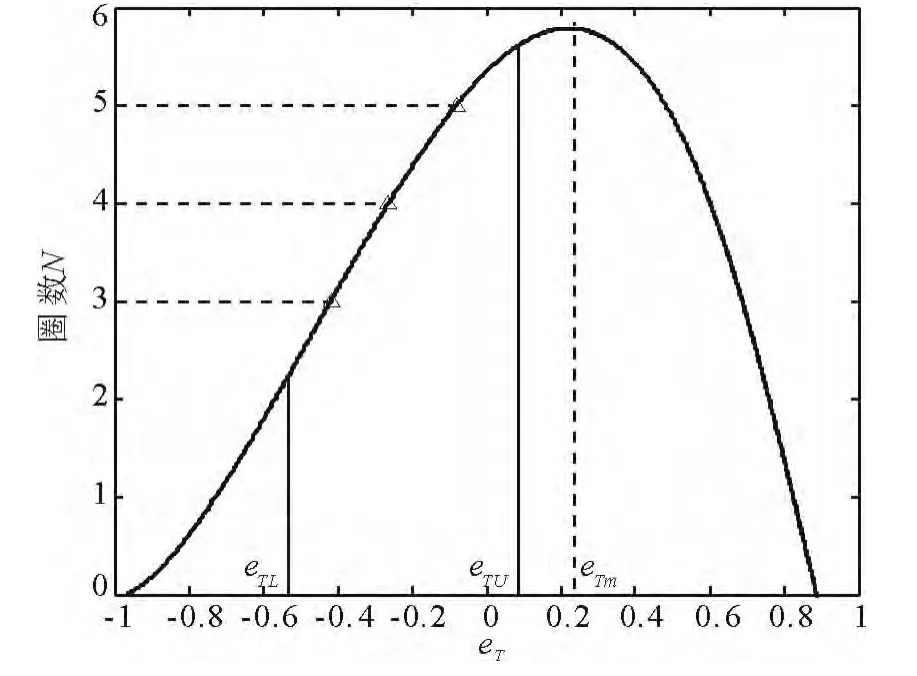
图6 轨道运行圈数Fig.6 Revolution number

5 算例与结果分析

取终端向量r1=RE+1 000 km，r2=1.5 r1，转移角为θ=2π/3，地球引力常数为μ=3.986×1014。图8为转移时间相对于eT的变化曲线。给定转移时间Δt=5×104s，首先由牛顿迭代法求解出所有11个可能的eT解(Nmax=5)作为验证的参考，如表2所示。

表2 所有多圈问题的解Tab.2 All solutions for multiple － revolution problem

现在考虑施加约束，令Rp=RE+350 km，Ra=RE+20 000 km，图7给出f函数与F函数随eT的变化曲线。由式(37)解出eTp1=－0.765 5，eTp2=0.083 5，eTa1= － 0.532 9，eTa2=0.762 2，由式(38)得满足约束条件的轨道必须位于范围eT∈(－0.532 9，0.083 5)内。轨道长、短径分界点为=0.254 7。约束边界处轨道圈数满足「N(eTL)⏋ =3，⎿N(eTU)」=5，故可行轨道满足 N=3，4，5。分别对3条轨道以eTL= －0.532 9为初始猜测进行迭代计算，结果分别收敛至eT3，eT4和eT5，迭代次数分别为 4，5，5 次。至此，得到了全部11个解中满足工程约束的3条可行轨道，且3条可行的轨道皆为短径轨道。所求出的轨道解如图8中上三角符号所示。

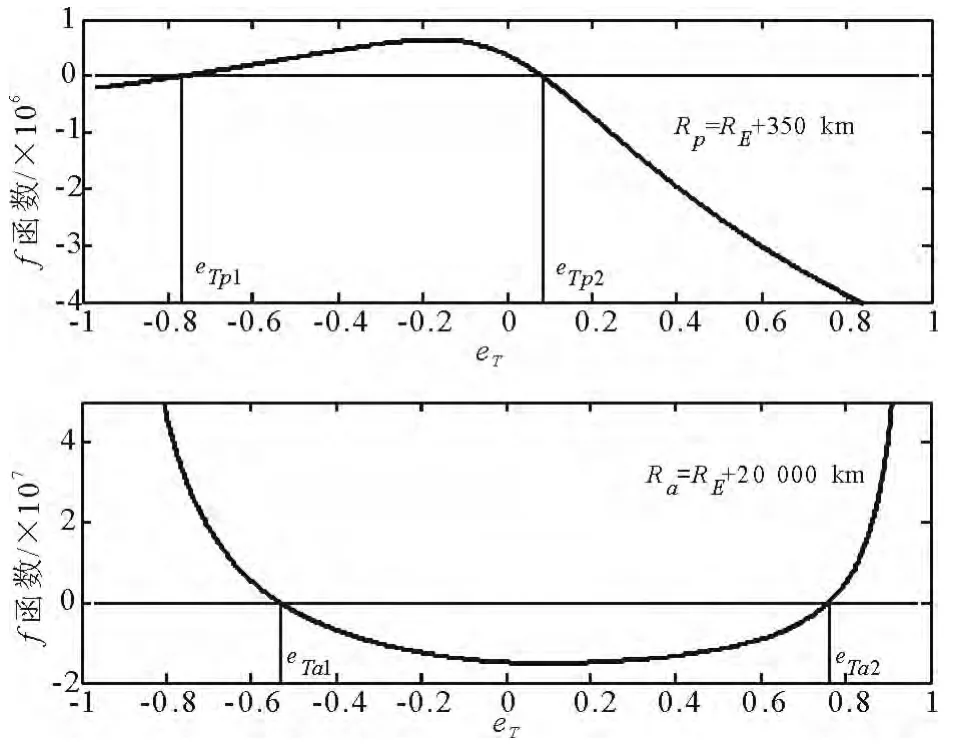
图7 两种约束函数随eT的变化关系Fig.7 Constrain functions versus eT

图8 转移时间对比eT及可行解Fig.8 Transfer time versus eTand feasible solutions

6 结 论

本文研究了考虑工程约束的多圈Lambert问题，建立了使用eT描述Lambert问题的整个参数体系，证明了两约束函数在eT的区间内最多只有一次增减性的变化，从而可以分别使用其与上下限的两个交点作为eT的界限，缩小搜索范围。使用约束边界作为迭代计算的初始猜测，可直接解算出满足约束条件的解，排除不可行解。与之前使用半长轴a作为积分变量分析约束函数相比，本文采用的方法所需解算次数更少，且更加简单有效，避免了大量的讨论过程。数值算例验证了本文所述方法的简便性与有效性。

[1]BATTIN R.An Introduction to the Mathematics and Methods of Astrodynamics[M].Revised Edition ed.Reston，VA:AIAA Education Series，AIAA，1999:295－297.

[2]LANCASTER R，BLANCHARD C.A Unified Form of Lambert's Theorem [R].NASA Technical Note，1969D－5368.

[3]BATTIN R H，VAUGHAN R M.An elegant lambert algorithm [J].Journal of Guidance，Control，and Dynamics，1984，7(6):662－670.

[4]SUN F T.On The Minimal Time Trajectory and Multiple Solutions of Lambert's Problem [R].Provincetown:AAS/AIAA Astrodynamics Specialists Conference，1979.

[5]NELSON S L，ZARCHAN P.Alternative approach to the solution of lambert's problem [J].Journal of Guidance，Control，and Dynamics，1992，15(4):1003－1009.

[6]AHN J，LEE S.Lambert algorithm using analytic gradients [J].Journal of Guidance，Control，and Dynamics，2013，36:1751－1761.

[7]AVANZINI G.A simple lambert algorithm [J].Journal of Guidance，Control，and Dynamics，2008，31(6):1587－1594.

[8]HE Q，LI J，HAN C.Multiple－Revolution solutions of the transverse－eccentricity－based lambert problem[J].Journal of Guidance，Control，and Dynamics，2010，33(1):265－268.

[9]ZHANG G，MORTARI D.Constrained multiple－revolution lambert's problem[J].Journal of Guidance，Control，and Dynamics，2010，33(6):1776－1784.

[10]PRUSSING J E.A class of optimal two－impulse rendezvous using multiple－revolution lambert solutions[J].The Journal of the Astronautical Sciences，2000，48(2 － 3):131－148.