韧性材料的微裂纹扩展与分叉的晶体相场模拟

高英俊， 罗志荣， 邓芊芊， 黄礼琳， 林 葵

（1.广西大学广西有色金属及特色材料加工重点实验室，南宁 530004；2.广西大学物理科学与工程技术学院，南宁 530004）

韧性材料的微裂纹扩展与分叉的晶体相场模拟

高英俊1，2， 罗志荣1，2， 邓芊芊1， 黄礼琳1， 林 葵1

（1.广西大学广西有色金属及特色材料加工重点实验室，南宁 530004；2.广西大学物理科学与工程技术学院，南宁 530004）

采用晶体相场方法研究韧性单晶材料在双轴拉伸条件下微裂纹扩展与分叉的演化过程，分析应变、温度、初始裂口形状等因素对裂纹扩展和分叉的影响.结果表明：对于简单的单向拉伸，应变需要达到一定的临界值，裂纹扩展才会启动.对于二组相互垂直的双轴拉伸作用，当应变达到临界值后，裂纹扩展过程中会发生分叉现象.温度越高，裂纹扩展越快且分叉越多.裂纹在扩展过程中，体系能量不断降低，当裂纹出现分叉时，体系能量降低得更快.在裂纹扩展过程中，有时是会在裂尖处前方出现微小的空洞，类似在裂纹尖端前方出现位错发射情况，这些微小的空洞逐渐扩大连成裂纹.本文所得结果与相关模拟结果和实验结果符合.

晶体相场方法；微裂纹扩展；应变；韧性材料

0 引言

材料在介观和宏观尺度上的性能在很大程度上由其内部的微观缺陷，例如，空位、空洞、位错、晶界和微裂纹所决定.这些缺陷起因于在原子尺度发生的复杂非平衡动力学过程.就目前所采用的多尺度模拟方法来说，对这些微观特征结构的实时演化过程的建模和模拟是一个重大挑战.相场方法是当今研究微观结构演化的强有力的数值计算方法［1－2］.传统的相场方法［3－7］是建立在平衡态均匀场的基础上的，忽略了许多由原子的周期排列结构产生的物理特性，难以反映晶体学结构特性以及原子尺度的行为信息，因而无法从根本上阐明微观组织演化过程中原子尺度上的动力学机理.虽然，目前可用分子动力学方法［8－9］模拟预测这些微结构演化动力学过程，且能准确地描述这些现象，但该方法适用的特征时间尺度主要在原子振动时间尺度（10－12到10－14秒），不易拓展到扩散时间尺度（10－6秒），并且，分子动力学要求加载的应变率很大，通常达到107～1010s－1，与实际工业的应变速度102s－1相差甚远［10，11］.最近，Elder等［11－13］基于密度泛函理论提出了晶体相场（phase-field-crystal，PFC）模型.该模型给出了新的自由能函数形式，引入的序参量为局域密度场，它将无序相（例如液相等）的密度场定义为一常数，将固相的密度场表示成周期性函数（波）的形式，进而通过周期的原子密度函数表现晶体的晶格结构.这样的周期结构的密度场就很自然地与弹性效应、晶粒取向和位错的运动等由周期结构产生的物理特性紧密地关联起来［13］.PFC模型既可以描述晶体学结构特性以及原子尺度的行为，又可以揭示时间尺度为10－6秒量级的原子、缺陷运动的行为特征.由此可以预见，PFC方法在今后的微结构演化的研究中将展现其强大的优势，能够广泛地应用到材料微结构研究的各个领域，为研究原子尺度组织结构的10－6秒量级的行为特征，例如研究晶体内部的空位、位错的运动、晶界的迁移和微裂纹扩展及其对材料宏观性能的影响，提供先进和强有力的计算方法.

目前，PFC方法已经有一些具体的应用，例如，模拟位错滑移和攀移［10］、相结构转变［14］、异质外延生长［15］、纳米晶粒长大［16］等.PFC方法最新的研究前沿和发展方向［17－21］之一主要集中在：将加工变形的外界作用因素引入PFC模型中，建立形变和位错动力学的PFC模型，用于超塑性、疲劳、断裂、蠕变等行为和性能的机理研究.尽管传统相场法和其它方法对材料的裂纹扩展研究已有较多的报道［22－25］，但是应用先进的PFC方法开展微裂纹扩展和分叉的研究工作还少见有报道.本文应用PFC方法模拟在双轴拉伸应变作用下纳米级微裂纹扩展与分叉的演化过程，详细分析应变、温度、初始缺口形状等因素对微裂纹扩展和分叉的影响.

1 PFC模型与方法

1.1 体系的能量密度函数

与传统的相场模型不同，PFC模型的自由能密度函数是通过对原子密度场变量取极小值得到的［11］.因此，该模型能够揭示晶体学结构特性以及原子尺度的行为.对于固态金属材料，其原子的位置不依赖于时间，呈规则排列.因此，要求相场变量必须能够反映原子周期性排列的特征.引入周期性相场变量，其局域位置的最大值对应于原子的位置；另一方面，液相中的原子位置随时间随机变化，取时间平均可看成为常量.符合这两方面要求的相场变量定义，可用保守的原子密度场函数作为相场变量，其表达式［11］可写成

式中，等号右边第一项反映晶格原子的周期排列结构特征，第二项反映液相的原子无规则运动，平均值为一个常量.此时体系无量纲的自由能函数［11］可以写成

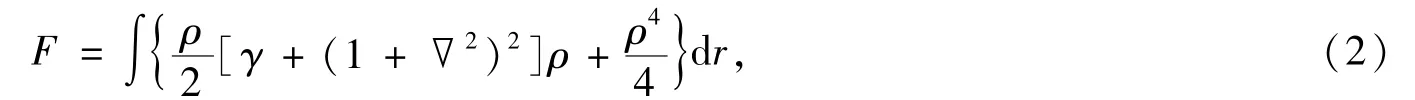
式中，γ是反映体系温度的参数，∇2为Laplace算子.该能量模型自洽地包含了晶体结构的物理特征，例如，多晶取向、弹性效应、塑性变形等.

1.2 二维体系的极小自由能密度函数

其中，ρ0和γ为体系自由能函数的两个重要参数.由体系的极小自由能密度函数，可以计算并画出体系不同相结构区的相图.对于二维体系，相区有均匀无序相和固相，且固相又有三角格子相和条状相两种，文献［11］已给出三角格子相和条状相的自由能函数形式.利用这些相的自由能函数，再按照平衡相图的计算方法得到的二维相图如图1（a）所示.其中，L、T和S分别代表均匀无序相、三角格子固相和条状固相.

1.3 演化动力学方程与数值化处理

保守的原子密度场变量的演化可用与时间相关的Cahn-Hilliard动力学方程描述

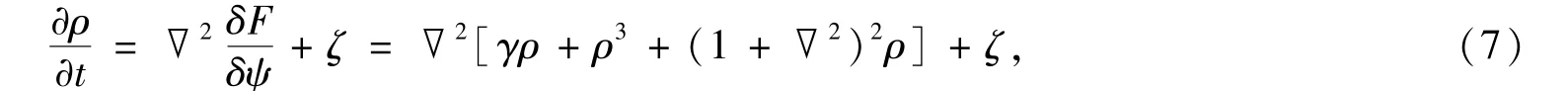
式中，ζ为高斯随机噪声项，具有零平均值．本文不需考虑ζ的作用.

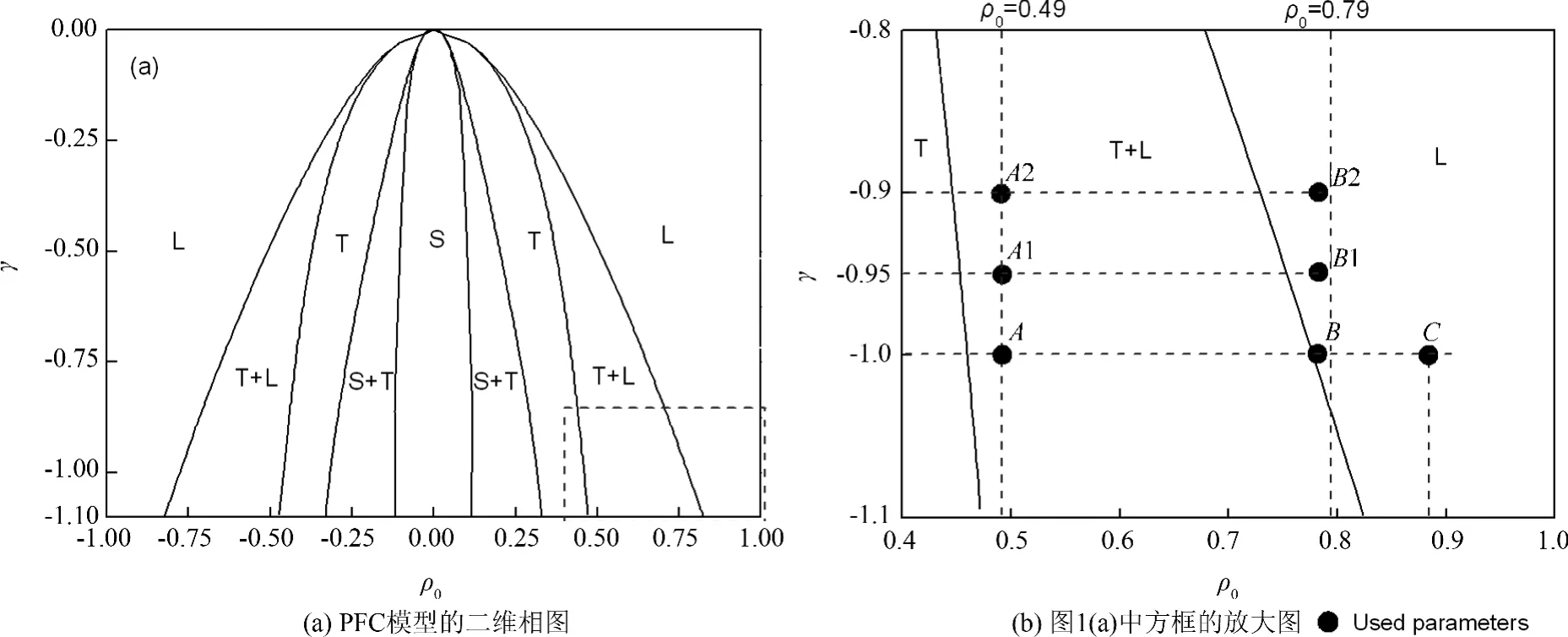
图1 （a）PFC模型的二维相图［11］；（b）（a）中方框的放大图Fig.1 （a）2D phase diagram of PFCmodel（b）Enlarged map of the rectangle block in（a）

为求解复杂的动力学方程式（7），还必须将动力学方程在时间和空间上进行离散化处理，即采用数值求解的办法.在本文的数值求解中，采用显型Euler迭代公式［26］

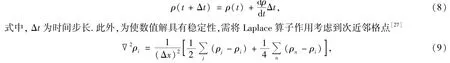
式中，Δx为空间步长，j和n分别代表i的最近邻格点与次近邻格点.

1.4 施加应变的方法

在受到拉伸作用后，样品中所有格点的坐标位置都会发生相应的变化.因此，可通过格点的坐标位置变换来反映应变的作用所引起的样品变形.设变形前的样品中格点位置的坐标用（x，y）表示，受拉伸作用引起变形后，格点位置的坐标用（x′，y′）表示．样品在x方向和y方向分别受到应变εx和εy的拉伸作用下，变形前后坐标变换关系为x′＝x／（1＋εx）和y′＝y／（1＋εy）．由于应变作用引起样品变形，其内部原子密度函数变为ρ（x′，y′） ＝ρ（x／（1＋εx），y／（1＋εy）），因此，在考虑应变作用引起变形的情况下，原子密度函数表达式（4）将变换为ρ（x′，y′），体系的能量也随之发生相应的变化，但控制演化的动力学方程的形式保持不变．将样品变形后的原子密度函数ρ（x′，y′）代入动力学方程（7）中，按照数值化计算步骤进行数值求解，然后进行可视化处理［5］，即可得到裂纹扩展的演化细节图.本文模拟不涉及具体材料的物性参数，所用参数均已无量纲化处理［11］，并将连续空间离散为四方格子，采用周期性边界条件.计算区域网格为1 024×512 gp（gp表示格子点数），空间步长设为Δx′＝Δy′＝π／3，时间步长Δt＝0.05，其它参数在下节中介绍.

1.5 初始裂口的设置

根据图1给出的相图，选取体系自由能密度函数的温度参数γ＝－1.0，原子密度参数ρ0＝0.49（图1（b）中的A点），位于液相与三角格子固相共存区.本文模拟单晶样品，其原子的排列方向与x轴夹角θ为15°.在样品的中心位置，挖出一个缺口作为初始裂纹的位置.为了便于比较，设置了两种初始裂口，分别为20×10 gp的长方形缺口和直径为16 gp的圆形缺口，缺口面积近似相等，其局部放大图如图2所示.缺口处周围的原子环境如图2（a）和2（c）所示，图2（b）和2（d）为缺口周围原子密度分布图.缺口处的参数设为γ＝－1.0，ρ0＝0.79（图1（b）中的B点），其正好处在液相与三角格子固相共存区附近的液相区.选取该点的参数的好处在于有利于三角晶相结构向裂纹结构转变.

图2 初始裂口的局部放大图（εx和εy分别为x方向和y方向的应变.）Fig.2 Local enlarged zone of initial crack rim（εxandεyare strains in x and y direction.）

2 结果与分析

2.1 应变对裂纹的影响

设置初始裂口为长方形，如图2（a）所示.图3为样品在y方向单轴拉伸作用下经过5.0×105ts（ts表示时间步数）演化的裂纹扩展情况，其中y方向的应变分别为εy＝7%、7.5%和8%.由图3（a）可见，对于单轴拉伸情况，当εy＜7.5%时，裂纹不扩展；当εy≥7.5%时，裂纹才开始扩展．由此可见，裂纹沿x方向扩展的临界应变约为7.5%.

图3 5.0×105ts时裂纹扩展情况（εx＝0%）Fig.3 Crack propagation at t＝5.0×105ts andεx＝0%

设置初始裂口为长方形，如图2（a）所示.样品同时受到x和y方向的双轴拉伸作用，设沿y方向的应变保持εy＝10%，沿x方向的应变分别为εx＝0%、3%、5%、7%、7.5%和8%，经过5.0×105ts演化的裂纹扩展分布如图4所示.由图4（a）可见，当εx＝0%时，裂纹扩展方向沿着原子间距最宽的方向进行，与x方向的夹角为15°，个别地方出现转折（图4（a1）），然后又恢复到原来的前进方向；图4（a1）给出了图4（a）的裂纹波折区域的放大图.由图4（a1）可见，裂纹的边缘与原子的排列方向平行，在转折处转折方向与原方向夹角约为60°.当εx＜5%时，裂纹不出现分叉，存在锯齿边缘，裂纹扩展的形状像一把“剑”.当εx＝5%时（图4（c）），在裂纹前端转折处，开始出现微小空洞（见图4（c）中圆形区域）.当εx＞7%时，裂纹在扩展中开始出现分叉，εx越大，分叉越多．例如，当εx＝8%时（图4（f）），由主裂纹分叉为子裂纹，子裂纹又分叉为孙子裂纹，形成了多枝状结构，且裂纹越来越宽.由图4中还可以看到在裂纹周围出现灰白波纹分布，这是在裂纹周围形成的原子位移的细微变化，反映了裂纹周围弹性应变场分布发生的畸变.图5是体系能量随时间的变化曲线.由此可见，应变εx越大，能量降低就越快，表明裂纹扩展也越快，分叉也越多．当εx较小时，能量变化曲线近似为直线，表明这一过程中，裂纹扩展过程不分叉．裂纹要出现分叉，施加的εx存在一个临界值，在本文设定的条件下，由图5可见，该εx的临界值接近7%．当εx＞7% 时，曲线下降速率明显加快，表明开始出现裂纹显著分叉．由图4的裂纹变化情况，可以看到裂纹演化的形状变化特征：开始时，施加的εx较小，裂纹形状像一把“剑”；随着应变εx增加，裂纹出现分叉扩展，逐渐长成“虾”状；最后，当εx≥8%时（图4（f）和（g）），出现多个分支结构，裂纹形状变成了“蟹”状.文献［28］也给出了类似的现象.

图4 5.0×105ts时裂纹扩展情况（εy＝10%）Fig.4 Crack propagation asεy＝10%at t＝5.0×105ts

图6给出了图4（b）中虚线方形区域内裂纹尖端B的扩展速率曲线.由该图可见，裂纹沿直线扩展过程中，速率较快，在转折处，裂纹扩展速率减小；从转折到恢复直线扩展，速率有一个加速突变的过程，然后又恢复到近似匀速运动过程.在转折处，出现速率振荡现象［29］，见图6中速率的峰和谷.由图5的变化趋势和图6速率的变化特点可以预测，当应变εx大于临界值后继续增加，则裂纹扩展速度加快，导致分叉更快、更多，将使得裂纹扩展速率出现更复杂的振荡情况.类似文献［29］指出的裂纹扩展速率超过临界值后，发生裂纹分叉，裂纹扩展速率出现振荡现象.

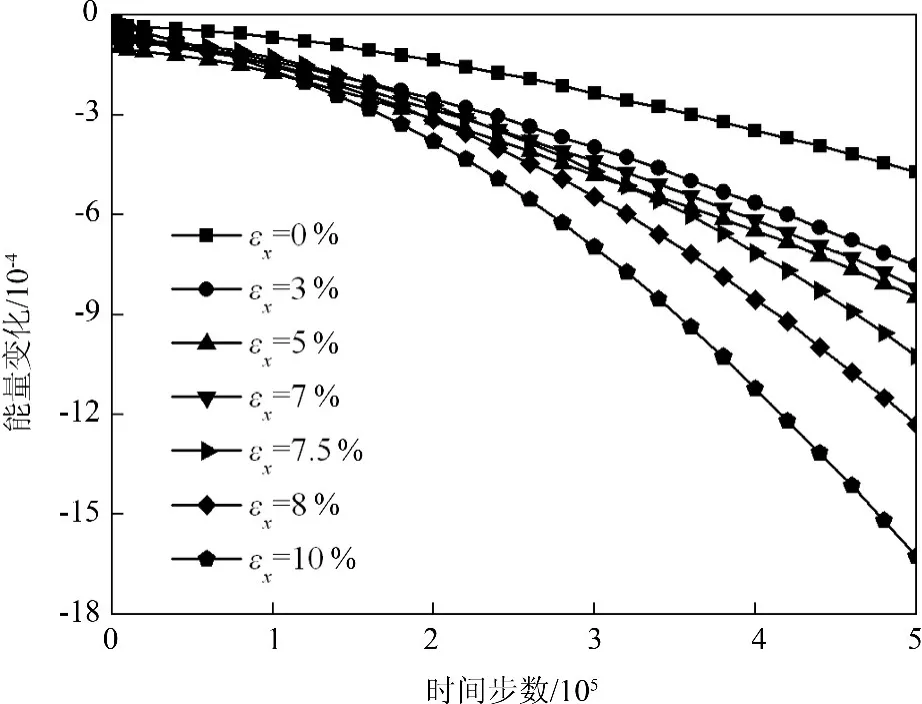
图5 不同εx对应的能量曲线（εy＝10%）Fig.5 Energy curves atεy＝10%and differentεx

图6 在图4（b）中虚线方形区域内裂纹尖端B的裂纹扩展速率振荡曲线Fig.6 Oscillations of crack propagation in Fig.4（b）rectangle block at crack tip B

2.2 温度参数对裂纹扩展的影响

设置初始裂口为长方形，如图2（a）所示，在裂口处取ρ0＝0.79，温度参数分别取γ＝－1.0、－0.95和－0.90（分别对应图1（b）中的B点、B1点和B2点）得到3类样品.对样品施加的应变为εx＝8% 和εy＝10%.图7给出了演化4.0×10 ts时不同温度参数取值情况下的裂纹扩展形貌图.由图7（c）可见，γ＝－0.9对应温度较高的情况，裂纹扩展较快，分叉也较多；γ＝－1.0对应温度较低的情况，裂纹扩展较慢，分叉也较少．图8给出了三种温度参数值情况下的体系能量随时间的变化曲线．由图可见，体系能量随着演化时间增加而减小．γ＝－0.9时，能量曲线减小最快；γ＝－1.0时，能量减少最慢.在最初的演化时间里，能量曲线随时间线性地减小，经过一段时间后，曲线开始向下弯曲，能量降低有加速趋势，表明从此时开始，裂纹开始分叉，随后的裂纹扩展过程中，出现更多的裂纹分叉；裂纹扩展分叉越多，体系能量降低得越快.能量曲线降低的本质原因是由于弹性应变能的释放要比裂纹界面能（表面能）引起的能量增加要大得多，使得体系总能量随着裂纹长大不断降低，裂纹得以扩展.

图7 4.0×105ts时取不同温度参数值γ对应的裂纹扩展形貌图Fig.7 Crack propagation with different temperature parameterγat t＝4.0×105ts

2.3 初始裂口形状及周围原子密度的影响

设置的初始裂口为圆形，如图2（c）所示.同时施加的应变为εx＝8%和εy＝10%，温度参数γ＝－1.0．为研究初始裂口处的原子密度的影响，裂口处的初始原子密度ρ0设置了两种值，分别为0.79（图1（b）中的B点）和0.90（图1（b）中的C点）.图10（a）和（b）分别给出了这两种ρ0参数下演化5.0×105ts时的裂纹分叉形貌图.从图10可见，ρ0＝0.90时，裂纹分叉较多，分枝较丰富，沿x方向和沿y方向都发展较快，且发展较均衡；而ρ0＝0.79时，相对而言裂纹沿x方向的发展较快，而沿y方向扩展较慢．由图9能量曲线变化可见，体系能量减小较快的是ρ0＝0.90情况．因为初始裂口处原子密度ρ0＝0.90比ρ0＝0.79偏离相图的晶相与均匀无序相共存区更远，不利于三角格子固相的稳定，而有利于裂纹的扩展.由图10还可见，在裂纹的扩展过程中，多个裂纹的子分枝出现锯齿折线结构.在分叉的地方，有的是先在分叉处前方出现微小的空洞，类似在裂纹尖端前出现位错发射，然后这些微小的空洞逐渐连成裂纹.这是由于裂纹尖端处存在非线性弹性与塑性变形作用而引起的现象，文献［30］也观察到类似的结果.

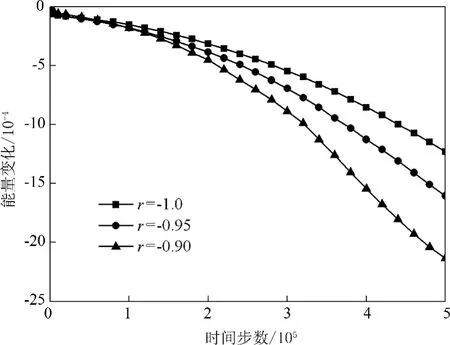
图8 取三种不同温度参数值（γ＝－1.0，－0.95和－0.90）对应的能量曲线Fig.8 Energy curves with different parameter（γ＝ －1.0， －0.95 and －0.90）

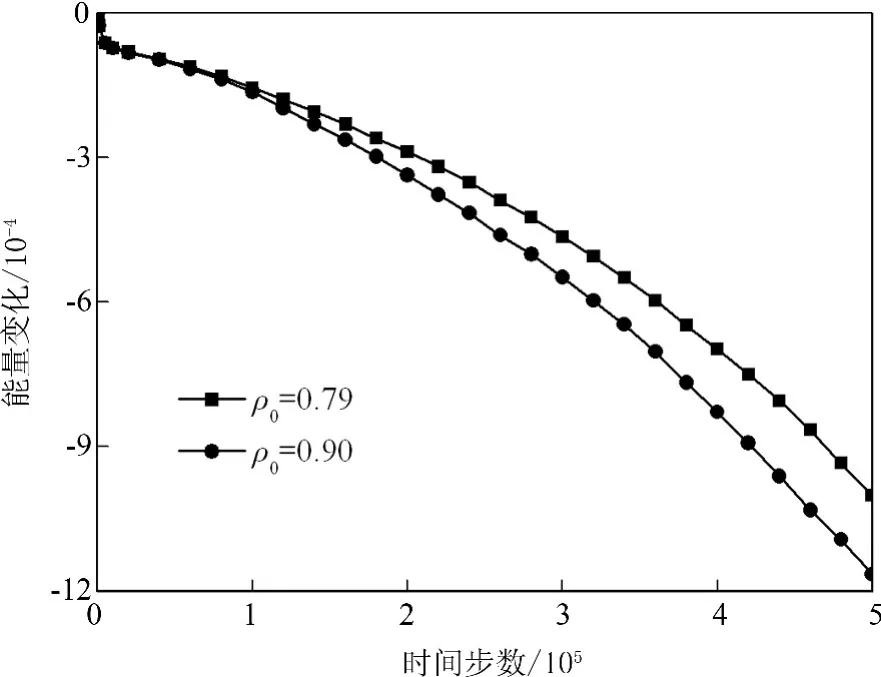
图9 初始圆形裂口处ρ0分别为0.79和0.90时的能量曲线Fig.9 Energy curves asρ0＝0.79 and 0.90 at circular crack rim

图10 圆形初始裂口在应变εx＝8%和εy＝10%情况下的裂纹形貌图（5.0×105ts）Fig.10 Crack propagation asεx＝8%andεy＝10%at circular crack rim

图10（a）与图4（f）所对应的设置条件，除了初始裂口形状不同，其它条件相同.对比两图可以发现，圆形裂口的裂纹沿x方向的扩展占有较明显的优势，而长方形缺口的裂纹较均匀的向四周扩展.主要原因是PFC方程的高度非线性和初始裂口形状不同将会导致裂纹周围的原子作用环境不同，可见，初始裂口形状，对裂纹扩展也有明显的影响［24］.

3 结论

采用PFC方法能够在原子空间尺度和扩散时间尺度较好地研究分析模拟韧性材料的裂纹扩展和分叉的详细过程和细节.主要结论如下：

1）裂纹的扩展方向沿着原子间距最宽的方向进行，施加的应变存在一个临界值，超过该临界值，裂纹扩展才得以启动；对于裂纹分叉，需要x和y方向的应变达到临界应变值才能出现裂纹分叉.

2）体系的温度参数取值较小时，则裂纹发展较快，分叉也较多.裂纹在扩展过程中，体系能量在不断下降；当裂纹出现分叉时，体系能量减少得更快.裂纹的子分枝出现锯齿折线结构，可看成裂纹扩展过程的振荡现象.在裂纹扩展过程中分叉的地方，有时是先在裂尖处前方出现微小的空洞，类似在裂纹尖端前方出现位错发射，然后逐渐连成裂纹.裂口处原子密度对裂纹扩展有明显影响.

3）裂纹扩展的形状变化特征：当施加单轴拉伸，应变较小时，裂纹形状像一把“剑”；同时施加x和y方向的双轴拉伸作用，随着应变增加，裂纹形状转变成“虾”状；最后，裂纹出现多个分支结构，裂纹形状变成了“蟹”状.

［1］Moelans N，Blanpain B，Wollants P.An introduction to phase-fieldmodeling ofmicrostructure evolution［J］.Calphad，2008，32：268－294.

［2］Wang Y，Li J.Phase field modeling of defects and deformation［J］.Acta Mater，2010，58：1212－1235.

［3］Chen LQ.Phase-field models formicrostructure evolution［J］.Annu Rev Mater Res，2002，32：113－140.

［4］Steinbach I.Phase-field models in materials science［J］.Modell Simul Mater Sci Eng，2009，17：73001.

［5］高英俊，罗志荣，胡项英，等.相场方法模拟AZ31镁合金的静态再结晶过程［J］.金属学报，2010，46：1161－1172.

［6］罗炳池，王海鹏，魏炳波.液态三元Ni-Cu-Pb偏晶合金相分离的相场模拟 ［J］.科学通报，2009，54：7－11.

［7］王锦程，李俊杰，杨玉娟，等.定向凝固界面形态演化及其稳定性的相场法研究 ［J］.中国科学：E辑，2009，38：16－23.

［8］Millett P C，Selvam R P，Saxena A.Molecular dynamics simulations of grain size stabilization in nanocrystallinematerials by addition of dopants［J］.Acta Meterialia，2006，54：297－303.

［9］Holm E A，Foiles SM.How grain growth stops：A mechanism for grain-growth stagnation in pure materials［J］.Science，2010，328：1138.

［10］杨涛，陈铮，董卫平.应力诱发双位错组亚晶界湮没的晶体相场模拟［J］.金属学报，2011，47：1301－1306.

［11］Elder K R，Grant M.Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals［J］. Phys Rev E，2004，70：051605－20.

［12］Elder K R，KatakowskiM，Haataja M，GrantM.Modeling elasticity in crystal growth［J］.Phys Rev Lett，2002，88：245701－5.

［13］Berry J，GrantM，Elder K R.Diffusive atomistic dynamics of edge dislocations in two dimensions［J］.Phys Rev E，2006，73：031609－16.

［14］高英俊，罗志荣，黄创高，等.晶体相场法研究二维六角结构向正方结构转变 ［J］.物理学报，2013，62（5）：050507－010.

［15］Yu Y M，Backofen R，Voigt A.Morphological instability of heteroepitaxial growth on vicinal substrates：A phase-field crystal study［J］.JCryst Growth，2011，318：18－22.

［16］Gao Y J，Wang JF，Luo ZR，Lu Q H，Liu Y.Nano-twin structure simulation with phase field crystalmethod［J］.Chinese JComputational Physics，2013，30（4）：577－581.

［17］Stefanovic P，Haataja M，Provatas N.Phase field crystal study of deformation and plasticity in nanocrystallinematerials［J］. Phys Rev E，2009，80：046107.

［18］Chan PY，Tsekenis G，Dantzig J，et al.Plasticity and dislocation dynamics in a phase field crystalmodel［J］.Phys Rev Lett，2010，105：015502.

［19］Huang Z F，Elder K R，Provatas N.Phase-field-crystal dynamics for binary systems：Derivation from dynamical density functional theory，amplitude equation formalism，and applications to alloy heterostructures［J］.Phys Rev E，2010，82：21605.

［20］Jaatinen A，Ala-Nissila T.Eighth-order phase-field-crystalmodel for two-dimensional crystallization［J］.Phys Rev E，2010，82：061602.

［21］Hakim V，Karma A.Laws of crackmotion and phase-fieldmodels of fracture［J］.JMech Phys Solid，2009，57：342－368.

［22］Spatschek R，Brener E，Karma A.Phase field modeling of crack propagation［J］.Philos Mag，2011，91：75－95.

［23］高英俊，罗志荣，黄礼琳，林葵.韧性材料的微裂纹扩展和连通的相场方法模拟 ［J］.中国有色金属学报，2013，23（7）：1892－1899.

［24］Huang S，Zhang S，Belytschko T，et al.Mechanics of nanocrack：Fracture，dislocation emission，and amorphization［J］.J Mech Phys Solids，2009，57：840－850.

［25］Livne A，Bouchbinder E，Svetlizky I，et al.The near-tip fields of fast cracks［J］.Science，2010，327：1359－1363.

［26］Chen L Q，YangW.Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters：The grain-growth kinetics［J］.Phys Rev B，1994，50：15752－15756.

［27］Oono Y，PuriS.Computationally efficientmodeling ofordering ofquenched phases［J］.Phys Rev Lett，1987，58：836－839.

［28］Imbeni V，Kruzic J J，Marshall G W，et al.The dentin—enamel junction and the fracture of human teeth［J］.Nature Materials，2005，4：229－232.

［29］Sharon E，Fineberg J.Confirming the continuum theory of dynamic brittle fracture for fast cracks［J］.Nature，1999，397：333－335.

［30］Buehler MJ，Abraham F F，Gao H J.Hyperelasticity governs dynamic fracture at a critical length scale［J］.Nature，2003，426：141－146.

date：2013－08－21；Revised date：2013－11－25

Phase-Field-Crystal Modeling of Microcrack Propagation and Branching in Ductile Materials

GAO Yingjun1，2，LUO Zhirong1，2，DENG Qianqian1，HUANG Lilin1，LIN Kui1
（1．Guangxi Key Laboratory for Non-ferrousMetal and Featured Materials，Guangxi University，Nanning 530004，China；2．College of Physics Science and Engineering，Guangxi University，Nanning 530004，China）

Morphology ofmicrocrack propagation and crack branching of single crystal ductile materials under tensile are simulated with phase-field-crystalmethod.It shows that shape of notch has a strong effect on crack propagation.With uniaxial tension crack propagation appears if only strain reaches a critical value.With biaxial tension a crack branches if only strain reaches a critical value. Temperature parameter takes significant effects on crack propagation.The smaller the temperature parameter is（the temperature is higher），the faster the cracks propagate and themore the crack branches are.It is observed that free energy of system decreaseswith time and decreases faster after crack starts to branch.During crack propagation，disconnectedly isolated cavities around themain cracks can be found and these defects become new cracks.They grow up along a line and become a branching crack.Simulated results are in agreementwith other simulations and experimental results.

phase-field-crystalmethod；microcrack propagation；strain；ductilematerials

TG111.5

A

1001-246X（2014）04-0471-08

2013－08－21；

2013－11－25

国家自然科学基金（51161003）；广西自然科学基金重点项目（2012GXNSFDA053001）；广西大学广西有色金属及特色材料加工重点实验室开放基金（GXKFJ12-01）及广西大学科研基金（XJZ110611）资助项目

高英俊（1962－），男，博士，教授，博士生导师，主要从事材料微结构设计与计算模拟实验研究，E-mail：gaoyj＠gxu.edu.cn