非均质低渗透油藏非线性流动数值模拟

姚 军， 黄 涛， 黄朝琴

（中国石油大学（华东）石油工程学院，山东青岛 266580）

非均质低渗透油藏非线性流动数值模拟

姚 军， 黄 涛， 黄朝琴

（中国石油大学（华东）石油工程学院，山东青岛 266580）

提出一种适用于非均质低渗透油藏非线性流动数值模拟的方法.通过引入单元边界压力和速度两组物理量，在单个网格单元中构造数值计算格式，可精确地获取每个网格单元的压力梯度.以单相非线性渗流问题为出发点，详细阐述该方法的基本原理；通过数值算例验证方法的正确性和适用性.

非均质；低渗透油藏；非线性渗流；油藏数值模拟

0 引言

随着我国油气田勘探开发的不断深入，低渗透油藏已成为我国增储上产的主要领域［1］.大量低渗透渗流实验和生产实践表明［2－4］：油气流动存在最小启动压力梯度，其渗流曲线偏离了经典的达西定律，具有显著的非线性特征.许多专家学者对其流动机理进行了大量研究，提出了多种非线性渗流模式，包括拟启动压力梯度模型、三阶段模型、非线性连续性模型等［5－7］，并进行了相应的数值模拟研究［8－11］.现有的低渗透油藏非线性流动数值模拟，大都是采用传统的有限差分法或控制体积有限差分.此类方法均基于相邻单元中心点的物理量值来构造数值计算格式，求取驱替压力梯度，进而结合渗流曲线来进行判断和求解.然而，对于非均质低渗透油藏，不同区域甚至不同网格单元的渗流模式不尽相同，数值模拟中必须获取各网格单元的压力梯度，并选择相应的渗流模式，此时上述传统的数值计算方法已无法满足要求.

对此，在控制体积有限差分法的基础上，通过引入界面中心点压力，提出了一种新的数值算法.该算法基于单个网格单元来构造数值计算格式，能够精确地获取每一网格单元的压力梯度，单元间则通过流量连续条件联系起来.并以此为基础，建立了一套非均质低渗透油藏非线性流动数值模拟方法.

1 渗流数学模型

由于受启动压力梯度的影响，低渗透油藏流体流动存在明显的动边界［12－13］.实验结果表明［14］：低渗透油藏渗流模式一般为如图1所示的渗流曲线（实线OA－AE），A点表示孔隙介质中最大孔道中的流体流动时的启动压力梯度，B点表示最小孔道中流体流动时所需的启动压力梯度，曲线AD上一点Di的平均启动压力梯度为Ci，C为直线DE与横坐标轴的交点，即拟启动压力梯度，D为曲线转直线的折点.

之前很多研究采用简化的拟启动压力梯度渗流模式，即用直线OC、CE来描述渗流过程.拟启动压力梯度模型在计算时对于在低压力梯度时阻力较小的大孔道中的流动估计偏低，因而综合经济技术指标会偏低.考虑某一封闭低渗透油藏区域Ω中的不可压缩单相液体的等温渗流过程，为简单起见，本文仅研究各向同性问题，并假设岩石微可压缩，对于拟启动压力梯度其数学模型如下：

图1 典型非达西渗流曲线Fig.1 Non-Darcy flow curve

其中，υ为渗流速度，K为渗透率张量，μ为流体粘度，p为油藏压力（或流动势），λ为启动压力梯度，φ为岩石孔隙度，q表示源汇项.

对于实际非线性渗流曲线（图1实线部分），文献［15－17］建议采用动态渗透率的概念，即渗透率和启动压力梯度是随着压力梯度的增大而增大的，当压力梯度大于某一临界值时渗透率和启动压力梯度不再发生变化，如图2所示.此时，可求出每个驱替压力梯度对应的渗透率及启动压力梯度，具体如下：①由岩心做出低渗介质渗流曲线图；②由驱替压力梯度，找到对应于渗流曲线上的渗流点；③对该渗流点沿渗流曲线方向做切线，该切线的斜率即为渗透率，而切线与驱替压力梯度坐标轴的交点即为该压力梯度时孔道的启动压力梯度.显然，对于动态渗透率模型，每一个压力梯度值对应一个拟启动压力梯度模型，因此，本文将重点阐述拟启动压力梯度渗流数学模型及其数值求解方法.对于图2实线所示的非线性渗流模式，其渗流数学模型仅需改变方程（1），其中，在曲线AD段渗透率是驱替压力梯度函数，具体如下

图2 渗透介质的渗透率随压力梯度的变化Fig.2 Mutative permeability vs.pressuregradient

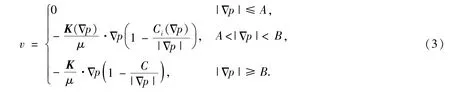
2 数值计算格式构造

假设油藏区域Ω∈R2被一组互不重叠的多边形网格Ω＝｛Ωi｝所剖分，如图3所示.

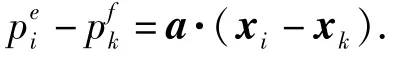
图3 网格单元分析示意图Fig.3 Schematic of grid analysis

由方程（1）易知边界面上的法向渗流速度vf与压力梯度Δp、启动压力梯度λ之间有

然，方程（15）中的第一行对应于方程（1）Darcy定律，第二行对应于方程（2）质量守恒定律，第三行则表征了单元边界面上的法向速度连续性条件.上述方程的系数矩阵表达式：

其中，Ne为网格单元总数；Ii＝Em．从方程（16）可知：方程（15）中的各系数矩阵仅与网格单元的几何信息和油藏参数有关，而对网格的几何形状没有特殊要求，求解方便，原则上适用于任何复杂网格.并且方程（14）中启动压力项只与每个网格单元有关，对于非均质油藏只需改变每个单元启动压力梯度，所以具有很好的适应性.

3 数值算例

通过简单的二维单相流算例对低渗透油藏数值模拟进行分析.考虑如图4（a）所示二维1／4五点井网模型，油藏长100 m，宽100 m，在（0，0）点有一注入井，在（100，100）点有一采出井，注入和采出的速度均为17.28 m3·d－1.采用三角网格剖分，节点数为190，单元数为330，如图4（b）所示.

图4 油藏几何信息图Fig.4 Reservoir geometry information

3.1 算例1

拟启动压力梯度模型：设渗透率Kx＝Ky＝0.1 md（10－3μm2），Kxy＝Kyx＝0，初始油藏压力Pe＝Pf＝10 MPa，拟启动压力梯度λ＝0.1 MPa·m－1，岩石压缩系数Cf＝8.64×10－4MPa－1，流体粘度μ＝1 mPa·s，t＝200 d（天）.

从图5可以看出，在拟启动压力梯度模型渗流过程中，存在明显的动边界，当驱替压力小于启动压力时，油藏中的流体是不流动的，油藏压力保持初始值不变.当压力传播到整个油藏时，会形成优势通道，流体流速较快.

图5 算例1压力及速度分布Fig.5 Distributions of pressure and velocity in Example 1

3.2 算例2

非线性渗流模型：该模型与上述拟启动压力梯度模型基本相同，唯一区别是，渗透率和启动压力梯度随驱替压力梯度增大而增大，当达到某一临界值时保持不变，其对应关系见表1.图6为非线性渗流模型不同时刻压力及速度分布图.

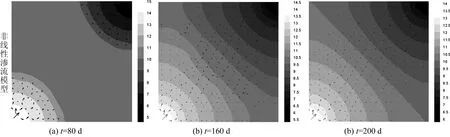
图6 算例2压力及速度分布Fig.6 Distributions of pressure and velocity in Example 2

如图7所示，对比两个模型不同时间步t＝80、160、200 d注采井点连线之间压力分布，可看出拟启动压力梯度模型在同一时间步中，压力传播范围较非线性渗流模型小，且靠近源点处相对于初始地层压力压差大；而在非线性渗流模型中，压力传播较快，油藏较早达到稳态.这是因为拟启动压力梯度模型是一种简化的渗流模式，模型假设了一个启动压力梯度（图1中的C点），当驱替压力梯度小于该启动压力梯度时，地层中的流体是不流动的.而实验结果表明实际渗流模式应为图1实线所示，当驱替压力梯度大于某值（图1中的A点）时，流体已经开始流动.所以说，对比2类模型，由于流体流动所需要的启动压力大，拟启动压力梯度模型在计算时对于在低压力梯度时阻力较小的大孔道中的流动估计偏低，因而综合经济技术指标会偏低，非线性渗流模型近似图1实线部分所示渗流模式，计算时更符合实际.

图7 不同时刻两种模型井间连线压力值Fig.7 Pressures between two model's wells

3.3 算例3

非线性渗流模式算例中均采用了相同的渗透率、启动压力梯度随驱替压力梯度变化曲线，对于非均质油藏，由于计算过程中针对每个网格单元均求出了驱替压力梯度，所以只要给定区块甚至网格单元的变化曲线，都可以求出网格单元相应的渗透率以及启动压力梯度，这也是该方法的优势所在，为了简单起见，均采用同一变化曲线，见表1.

考虑与算例2中非线性渗流相同的模型，唯一区别是其渗透率分布不同，在此算例中渗透率Kx、Ky通过MatLab的随机函数randn生成，Kxy＝Kyx＝0，如图8（a）所示，图8（b）、8（c）、8（d）为不同时刻压力及速度分布.

低渗透油藏非均质性极强，网格之间渗透率差别较大，如图8（a）所示.从数值模拟结果看出，流体主要沿着渗透率较大的网格流动、流速较大，压力传播快，符合实际，并且本文提出的方法适用于非均质性油藏.

图8 算例3压力及速度分布Fig.8 Distributions of pressure and velocity in Example 3

4 结论

1）提出一种适用于非均质低渗透油藏流动数值模拟方法，以单相渗流问题为出发点，详细阐述了方法的基本原理，并通过数值算例验证了方法的正确性.

2）新方法仅基于单个网格单元的信息来构造数值计算格式，理论上适用于任何复杂网格，可精确地获取每个网格单元的压力梯度，适用于非均质低渗透油藏数值模拟，尤其是不同区域或网格单元具有完全不同渗流模式的情形.

3）本文仅对非均质低渗透油藏的单相渗流问题予以研究，下一步将该方法推广至两相、多相渗流以及三维问题.

［1］Wang Guangfu，Liao Rongfeng，Li Jianglong，et al.The development situation and future of low permeability oil reservoirs of SINOPEC［J］.Petroleum Geology and Recovery Efficiency，2007，14（3）：84－89.

［2］Miller R J，Low P F.Threshold gradient for water flow in clay systems［J］.Soil Science Society of America Proceedings，963，27（6）：605－609.

［3］Lv Chengyuan，Wang Jian，Sun Zhigang，et al.An experimental study on starting pressure gradient of fluids flow in lowpermeability sandstone porous media［J］.Petroleum Exploration and Development，2002，29（2）：86－89.

［4］Wan Quanlin，Tan Hai，Lv Dongliang，et al.An experimental study on threshold pressure gradient in low permeability reservoir［J］.Petroleum Geology and Recovery Efficiency，2011，18（1）：97－100.

［5］Huang Yanzhang.Nonlinear percolation feature in low permeability reservoir［J］.Special Oil＆Gas Reservoirs，1997，4（1）：9－14.

［6］Yao Yuedong，Ge Jiali.Study on non Darcy flow pattern in low permeability oil reservoir［J］.Xinjiang Petroleum Geology，2000，21（3）：213－215.

［7］Xiao Zengli，Pu Chunsheng，Qin Wenlong，et al.Nonlinear percolation feature of low permeability reservoirs and its effect ［J］.Oil Drilling＆Production Technology，2007，29（3）：105－107.

［8］Guo Yongcun，Lu Detan，Ma Linxiao，et al.Numerical simulation of fluid flow in low permeability reservoir using finite difference method［J］.Journal of Hydrodynamics，2004，19（3）：288－293.

［9］Han Hongbao，Cheng Linsong，Zhang Minglu，et al.Physical simulation and numerical simulation of ultra-low permeability reservoir in consideration of starting pressure gradient［J］.Journal of University of Petroleum，China（Natural Science Edition），2004，28（6）：49－53.

［10］Xue Guoqing，Li Ming，Wang Daocheng，et al.Numerical simulation of low permeability and heterogeneous reservoir［J］. Fault-Block Oil and Gas Field，2007，14（4）：43－44.

［11］Yang Zhengmin，Yu Rongcheng，Su Zhixin，et al.Numerical simulation of the nonlinear flow in ultra-low permeability reservoirs［J］.Petroleum Exploration and Development，2010，7（1）：94－98.

［12］Guo Yongcun，Zeng Qinghong，Wang Zhongxun.Numerical simulation of low permeability flow with moving-boundary using meshless methods［J］.Engineering Mechanics，2006，23（11）：188－192.

［13］Liu Wenchao，Yao Jun，Wang Jianzhong.Front tracking for moving boundary of non-Darcy seepage flows in low-permeability porous media［J］.Chinese Journal of Computational Physics，2012，29（6）：823－827.

［14］Yan Qinglai，He Qiuxuan，Yu Ligang.A laboratory study on percolation characteristics of single phase flow in low-permeability reserviors［J］.Journal of Xi'an Petroleum Institute，1990，5（2）：1－6.

［15］Lei Qun，Xiong Wei，Yuan Jiangru，et al.Behavior of flow through low-permeability reservoirs［A］.SPE 113144，2008.

［16］Yao Jun，Liu Shun.Well test interpretation model based on mutative permeability effects for low-permeability reservoir［J］. Acta Petrolei Sinica，2009，30（3）：430－433.

［17］Yin Zhilin，Sun Wenjing，Yao Jun.Numerical simulation of the 3D oil-water phase dynamic permeability for low-permeability reservoirs［J］.Acta Petrolei Sinica，2011，32（1）：117－121.

Numerical Simulation of Nonlinear Flow in Heterogeneous and Low-permeability Reservoirs

YAO Jun，HUANG Tao，HUANG Zhaoqin
（School of Petroleum Engineering，China University of Petroleum，Qingdao 266580，China）

A numerical method is developed to model nonlinear flow in heterogeneous and low-permeability reservoirs.In order to obtain pressure gradient of each gridcells precisely，we introduced two sets of physical quantities，cell face pressures and surface efflux for each gridcell.Principle of the method is elaborated based on single-phase fluid flow problem.Several numerical examples are presented to demonstrate efficiency and applicability of the scheme.

heterogeneity；low-permeability reservoirs；nonlinear porous flow；numerical simulation

date：2013－10－15；Revised date：2014－02－19

TE348；TE319；O241.82

A

2013－10－15；

2014－02－19

国家重点基础研究发展计划（2011CB201004），国家自然科学基金（51234007），国家重大科技专项（2011ZX05014-005-003HZ）和中央高校基本科研业务费专项资金（13CX05007A，14CX02042A，13CX05017A，14CX06091A）资助项目

姚军（1964－），男，山东临沂，博士生导师，主要从事油气田开发工程教研工作，E-mail：RCOGFR_UPC＠126.com

1001-246X（2014）05-0552-07