一种适合基于原子尺度有限元方程的低通滤波边界条件

任国武， 汤铁钢， 李庆忠

（中国工程物理研究院流体物理研究所，四川绵阳 621999）

一种适合基于原子尺度有限元方程的低通滤波边界条件

任国武， 汤铁钢， 李庆忠

（中国工程物理研究院流体物理研究所，四川绵阳 621999）

发展一种基于原子尺度的有限元动力学方程，其动态行为跨越了从原子尺度到宏观尺度.理论计算该方程的色散关系和动力学散射特征.在此基础上，基于滤波器的概念，设计低通滤波边界条件用于减少网格增大带来的高频反射波，同时又保证低频振动波传播不受影响.通过一维数值模拟，计算了能量反射和透射系数，展示低通滤波边界条件可以吸收高频反射波而不影响低频波的传播.

有限元；滤波；反射系数

0 引言

多尺度模拟是一个复杂而非常活跃的研究领域，材料断裂、湍流现象等研究引起了广泛的关注.过去十多年间，不同研究者发展了多种多尺度方法［1］，跨越了从原子尺度到宏观尺度，在探索材料的断裂、位错等现象［2－12］的物理机制等方面取得了许多富有性的成果.多尺度方法的思想是在包含有非线性变形的区域采用精细的模拟方法，如第一性原理［4，10］或分子动力学，而在外围变形较小的区域采用近似的模拟方法，如有限元方法.然而，不同模拟尺度上物理模型的差异必然要带来耦合的问题，从而造成一些非物理的现象发生，比如虚假波反射［13］.

当前主要的目标是发展有限温度多尺度模拟方法模拟动力学问题，由于耦合边界造成的声子反射，从而造成边界区存在温度梯度，以至整个耦合体系很难达到热力学平衡.因此在耦合边界考虑有效的边界条件用于吸收这些虚假的高频反射很有必要.已有一些方法［14－21］解决这个问题，如精确边界条件、吸收边界条件等等.但是这些方法整体上是吸收来源于原子区域的所有振动模，包括在有限元区域体现长程相互作用的低频波.因而在整个模拟过程中还是限制于准静态过程，难以建立带有热力学耦合的多尺度模拟方法.

本工作中，我们发展一种基于原子尺度的有限元方法，利用发展的低通滤波边界条件来解决网格增加造成的虚假反射问题.数值模拟证实该方法能有效消除高频的反射波而不影响低频波传播.

1 模型及方法

我们建立的动力学有限元模型，如图1所示.考虑到初始整个模拟体系由无穷多个原子构成，可采用经典的Lagrangian力学来描写.在不考虑外力的作用下，该体系的Lagrangian量等于其动能减去势能，表示为

其中u是原子位移场，MA是原子质量mμ的对角矩阵，V（u）是原子体系的多体相互作用势.

现在把不同长度的单元分配到整个原子体系，由于外载作用下有些区域出现非线性变形，甚至有断裂键，采用细单元来描述，而有些区域则变形很小，可包含多个原子的大单元，由此整个原子体系的自由度就被减少.图1清晰展示了该体系局部某个区域内有些单元长度刚好为原子间距离，有些单元则包含多个原子.对于图1所示的一维模型，我们采用两节点的单元.为方便理论推导，每个单元的长度hl是原子距离aμ的整数倍，即hl＝nlaμ．依据动力学约束条件，每个单元内原子的位移场可以表示为u＝Jd，d是节点的位移场，J是一插值函数.利用该条件能实现整个体系自由度的减少.通过插值计算得到单元内所有原子的位移场.

图1 一维有限元模型示意图Fig.1 Schematic illustration of one-dimensional FE model

把原子和节点位移场关系代入式（1）后，求解在受约束后的有限元动力学方程，

其中M和K分别是质量矩阵和刚度矩阵，

从式（3）中可看出，质量矩阵与离散原子质量有关，刚度矩阵与原子间相互作用势能有关.因此，我们称式（2）为基于原子尺度的动力学方程（atomic-based finite element method，简写为AFEM）.

为了推导式（2）对应于图1有限元模型的具体形式，J选择为线性插值函数，一维情形下在节点k处为

其中，xk为节点k的位置，它是一个局域的函数，在节点处的值为1，而在次近邻节点以及次近邻单元之外其值为0.因此我们将利用J的定义来推导AFEM的质量和刚度矩阵形式，并与传统有限元求得矩阵作比较.

通过理论推导首先获得集成的AEFM质量矩阵形式为

其中，ζl＝（nl－1）（nl＋1）／6nl，ηl＝nl－2ζl，是一个三对角的质量矩阵，矩阵元值依赖于单元长度与原子间距比值nl.

同时计算了相应的刚度矩阵，从形式可以看出，它是依赖于原子体系的势函数，因而为了方便理论推导，选取的势函数只考虑了最近邻和次近邻的简谐相互作用

其中f1和f2分别为最近邻和次近邻的力常数.上面给出的刚度矩阵表达式具体写为

式（6）代入式（7）得到集成刚度矩阵为

由此得到了AFEM的质量和刚度矩阵，与网格单元的长度有关.当单元长度与原子间距离相等时，质量矩阵只含有对角元，刚度矩阵为五对角元，这与原子体系下获得动力学方程是相同的.当单元的长度为无穷大时，质量矩阵对应为连续情形下的一致质量矩阵，刚度矩阵退化为连续情形，此时AFEM运动方程过渡为连续弹性理论离散后的有限元方程.因此我们发展的一维AFEM模型建立了从原子区域过渡到连续区域，在靠近原子长度的单元，节点的相互作用展现了非局域的特性，节点的相互作用除了最近邻外，还包括了次近邻的作用；单元长度趋向无穷大时，此时节点作用表现为局域性，具有与传统有限元方法相同的性质.

2 AFEM方程的动力学行为

2.1 色散关系

基于理论推导得到的AFEM方程，可计算动力学色散关系.单元大小都相同且长度为hl，每个单元中包含的原子数目为nl个.在引入正则的平面波解di＝d0ei（qx－ωt）代入运动方程（2）后，得到对应的动力学方程.

所以，AFEM模型的频谱为

为了比较，我们也求得了在此条件下的传统有限元方法，由集中质量矩阵近似和连续弹性常数描述的动力学方程，

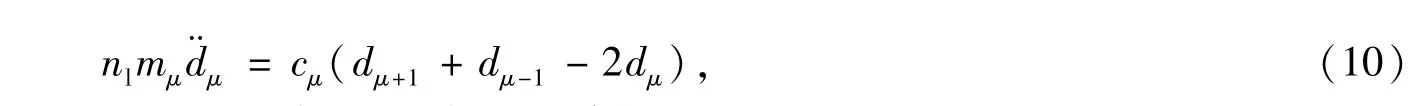
其中cμ＝（f1＋4f2）／nl．注意上式中的dμ为节点位移.对应的频谱表示为

原子模型的运动方程为

对应的声子谱是

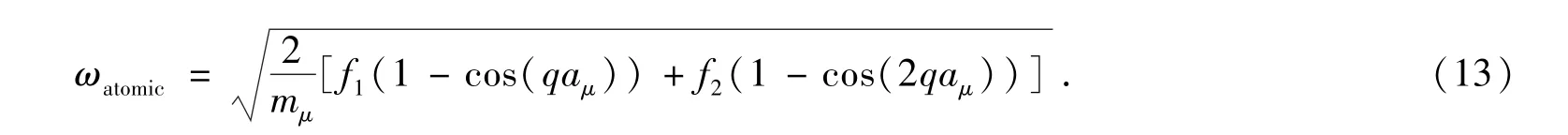
在图2，我们给出以上三种情况的频谱.计算中我们选择了有限元区域内每个单元的原子数目为20.在考虑周期性边界条件后，其相应Brillouin边界的波矢为π／20.由图中比较可以看出，在长波区域，也就是波矢q靠近0的区域，这三个方法得到频谱曲线相近.但是在靠近Brillouin边界时，AFEM模型计算的谱相对于原子模型的误差是低于传统有限元方法的，表明AFEM包括更多的与原子区域相同的振动模，并且AFEM模型在Brillouin内所得到的频谱是优于传统有限元方法.

2.2 反射系数

接下来分析AFEM方程的散射问题.由于单元长度的变化，在能量守恒的有限元区域，必然会有反射的发生，短波模不允许在整个区域中传播，因此这些非物理的反射波在动力学模拟过程中会造成局域的热，在界面产生温度梯度，而这些热会让整个体系处于非平衡的状态.我们将用散射方法来定量分析这个问题，即计算反射系数和透射系数.

为了方便计算，只考虑单元增大一倍的情形.入射波在细单元的区域，在节点k处单元增加，在界面出发生反射，一部份会继续传播到粗单元，而一部分会反射回细单元，因此在细单元和粗单元的位移为平面波形式

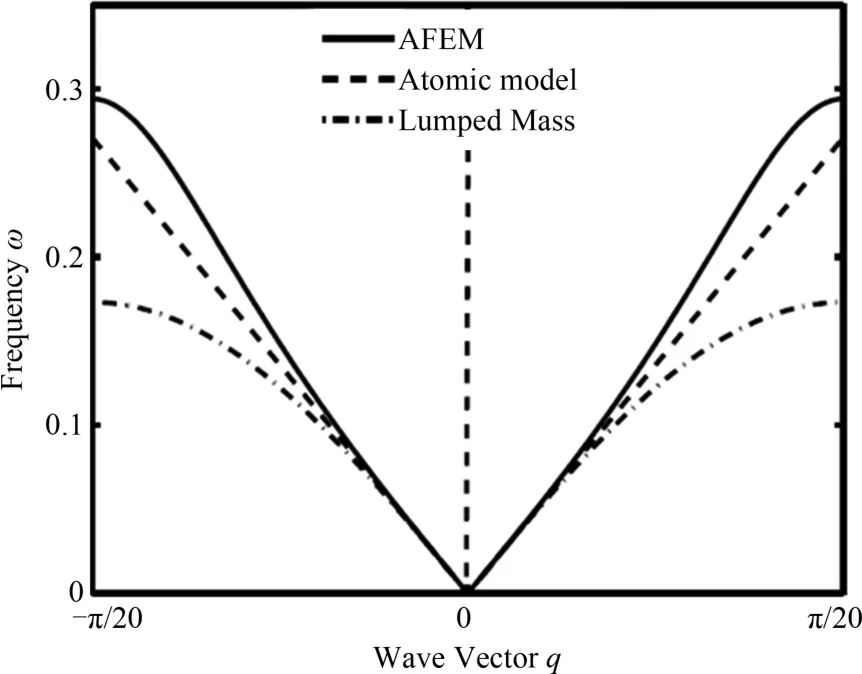
图2 AFEM、原子模型以及集中质量近似的有限元模型色散关系Fig.2 Dispersion relations of AFEM，atomic model and FE model with lumped mass approximation

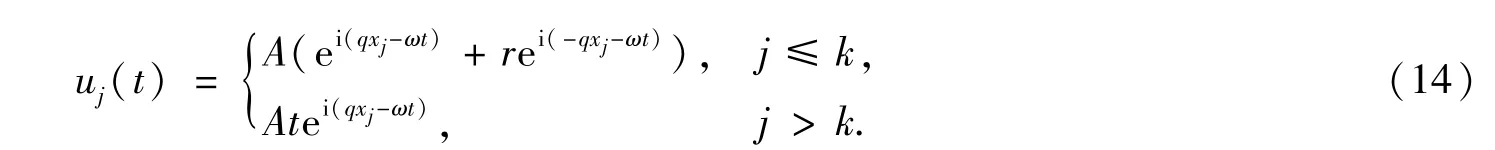
反射系数和透射系数则表达成R＝｜r｜2，T＝｜t｜2．波矢q与频率的关系经由动力学矩阵得到.至于系数A只是表示波的振幅大小，而反射系数和透射系数是个比值，因此可选择A等于1.虽然位移场是由多个频率组合而成，但由于方程是简谐性的，所以只考虑单频就可以了.把式（14）代入AFEM的运动方程（2）得到

式（15）是代表节点的运动方程.变换uj（t）为

注意节点的质量只有最近邻有作用，而节点的力作用项除了最近邻外还包括有次近邻作用.代入式（14）有

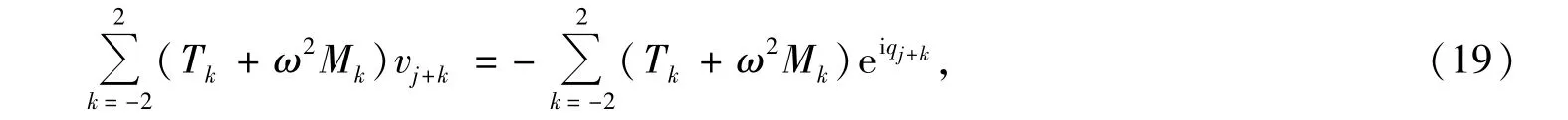
式（19）需要注意的是M项，只有在｜k｜＜2才不为零.表面上看，解决上式的v项需要求解所有的节点数才行，但是由于在远离单元突变的区域外，这些节点的v项是相等的，只是存在相位的差别.利用数值解得到相应的反射系数.

图3给出了随波矢变化的反射系数，同时也计算了集中质量近似下传统有限元方法的结果.从图可以看出，在采用AFEM后反射系数降低了很多.AFEM发生全反射时的最低频率为π／2，而传统有限元方法的最低频率为π／6.因此很显然，采用AFEM后意味着有更多的低频模能传播到粗单元的区域，降低了声子散射.然而，大量的高频振动模仍然被反射了，其携带的声子能量反射回细网格区域，造成这个区域的温度局域身高，从而导致整个包含有细和粗网格区域间出现能量梯度，体系处于非平衡热力学状态.这是一种非物理的热能，需要被消除.为此我们发展了一个基于低通滤波边界条件的方法用于耗散这些高频反射波.

图3 AFEM和集中质量近似的有限元模型反射系数Fig.3 Reflection coefficients of AFEM and FE with lumped mass approximation

3 低通滤波边界条件

滤波器方法在信号处理中有着广泛的应用，用来处理不同频率信号波的传播，在实际应用中加入一些适合的电子元件（如RLC电路），就可以实现哪些波通过，哪些波被消除，这种方法的理论指导就是在输入信号和输出信号之间构建一个传输函数.它的作用就是对输入信号进行过滤，得到需要的输出信号.这个方法一直被应用于电路中，近些年来，已经有学者把它应用到了计算模拟之中，获得生物分子中有用的原子振动信息.

3.1 理想传输函数

在动力学模拟中，每个原子的振动是随时间变化的，它们也可以被看成是一个信号，称为原子信号.原子的相互作用就是不同原子信号间的相互传播.因此在原子系统可构造在原子信号间传递的传输函数.

考虑最简单的一维模型，原子与原子间的相互作用只考虑最近邻简谐势来描述，其中力常数为k1，运动方程为

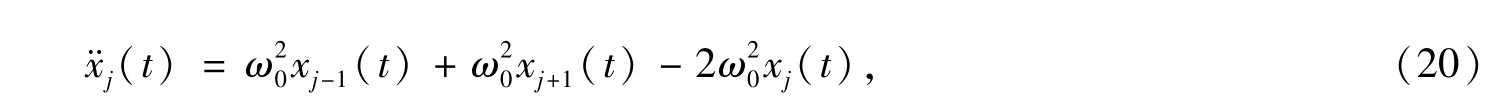
其中ω0

2＝k1／mμ，mμ为原子的质量．对于n个原子的体系，这样对应的方程有n个．在以下的推导中，令k1和mμ为单位1.经由Laplace变换，方程（20）可变换为

对于无穷长的原子链，且其中原子不受外力作用下，可近似θj＝θj＋1，得到

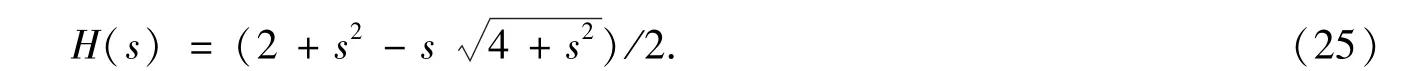
在频域空间，H（iω）的模为1，表明所有的振动模可无阻来回传播.注意到虽然H（s）的推导是基于无穷长原子链，但从定义看出它描述局域的近邻原子间振动传输关系.

3.2 低通滤波耗散边界条件

以上我们得到了理想原子模型情况下的传输函数，希望在这个模型的基础上设计一个与原子信号相关的低通滤波器来处理提出的虚假反射问题.所设计的滤波器依赖于AFEM得到的反射系数，目的是过滤掉在波矢大于π／nl时的全反射，而让低频的通过.在此情况中，通过色散关系变换反射系数与波矢的关系为反射系数与声子振动频率的关系.需要注意的是发生全反射时对应的频率为ωt.所以待设计的低通滤波器的要求是过滤掉频率大于ωt的波，而不影响低于这个频率波的传播.

通过一系列的设计和分析，得到满足要求的低通滤波器，其数学形式为

事实上，在得到这个结果前，我们已经做了其他耗散方法的低通特性测试，比如Lagevin耗散，获得其传输函数，在引入多个耗散层的条件下，得到了整体传输函数随频率的关系，给出其滤波特性，结果证实了添加一定数目的耗散项后，所有来源于原子区域的波都能被吸收掉.通过得到的传输函数，模拟中能定量分析如何加入耗散层过滤掉所有反射的波.

在频域空间，传输函数H（s）模随频率的变化如图4.在图4中，虚线是理想的滤波器设计，也就是如果能设计出大于ωt的波被完全过滤的滤波器，而不会影响低频波的传播，那将是最完美的，但是由于物理模型的限制，实际设计的滤波器由实线表示，显而易见它是一个低通的滤波器，虽然它也过滤掉了一些不该滤掉的低频波，但是对高频的过滤基本可满足要求，大大减少高频的反射.对我们而言，最为关心的是传输函数的模，事实上在实际模拟中，它对应于能量多少，而相位作用会带来色散效应，在这里暂时略去这方面的分析.其中的参数β虽说是一个可调参数，但是在分析中发现，它的大小不会影响滤波的特性，仍保持了低通滤波器的性质.在下面我们将给出详细的说明.

由低通滤波的数学形式，基于Laplace逆变换获得对应时空域下的运动方程，表示为

图4 传输函数与振动频率关系（虚线为理想的传输函数，实线为依赖实际原子模型的传输函数.）Fig.4 Schematic illustration of transfer function and vibrated frequency（The dashed line is an ideal transfer function while the solid line is a realistic one relying on atomic model.）

从等式（27）发现运动方程中多余的部分是近邻原子的速度二阶差分，由于这个方法是过滤高频的声子，而不影响低频声子传播，因此这个方法称为声子滤波器方法（PFM）.从运动方程中看出，这个低通滤波耗散方法只是比Lagevin耗散多了两个次近邻项，造成对低频的耗散影响变小.参数β的选择是非常重要的，在实际的应用中，可选择多个β项来耗散高频的反射波，一般而言，最好选择其值逐渐增加的原则，如果值太大，会出现过衰减的情况，反而会增强反射.

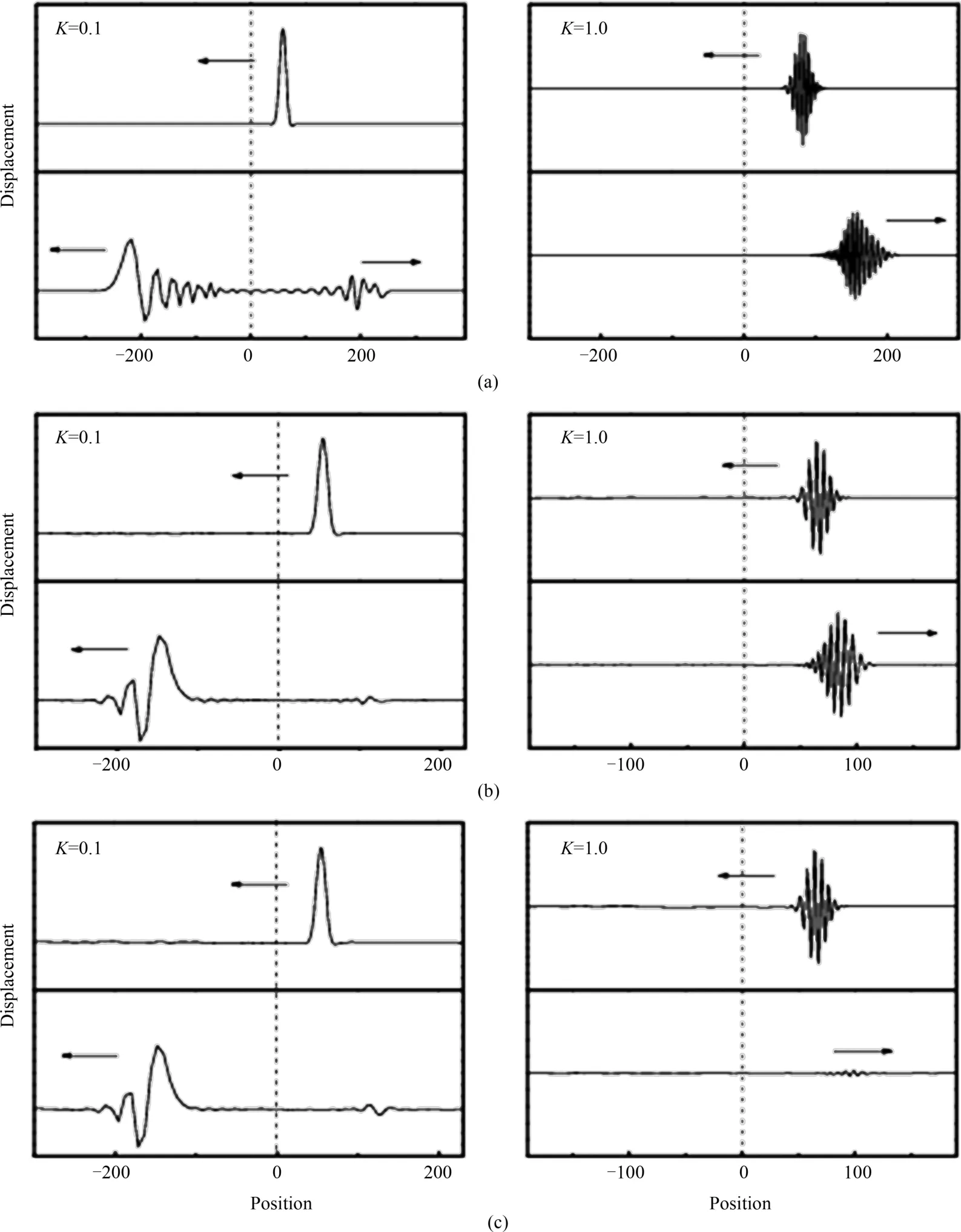
图5 波矢K＝0.1和K＝1.0的波包在一维模型中的传播，（a）集中质量近似的有限元方法，（b）AFEM，（c）AFEM加滤波耗散方法Fig.5 Wave-packet propagation of wave vectors of K＝0.1 and K＝1.0 in one-dimensional model，（a）lumped mass FE；（b）AFEM；（c）AFEM with PF method

通过理论的分析，以上得到的低通滤波耗散方法满足了要求，虽然与理想的情况差别很大，但是从本质上，这个传输函数展示了低通性质.而β项的选择，我们只是做了简单地分析.事实上，可以通过数值优化β来定出所需的传输函数满足理想情况，达到完全过滤掉高频波而不影响低频波的传播.

4 一维数值模拟结果

我们将实施一维有限元动力学模拟，模型如图1.在最左边是均匀大小的粗单元，然后往右逐渐变小至细单元，长度为原子间距.最长单元的长度是原子间距的8倍.在实施模拟开始时，整个区域的质量矩阵和刚度矩阵需要提前生成，而且在以后都不发生变化.速度－Verlet算法用于整个模型的时间积分.

在模拟过程中，我们将采用Gaussian波包作为测试信号，其形式

其中K是平均波矢.把这个波包作为初始位移加入细单元区域，x0是波包的中心位置，σ波包的宽度.

为了比较，模拟条件选择了三种：①传统有限元方法，集中质量近似；②AFEM；③AFEM＋声子滤波方法.采用了两个不同的波矢K＝0.1和K＝1.0作为测试输入.测试的结果如图5所示，对于图5中的每个子图，虚线表示的是网格逐渐增大的过渡区域，左边为粗网格区域，右边为细网格区域.每个图示的上下两个波包图，对应于两个时刻用于说明波包在从初始的原子区域以及经过过渡区域后到达的粗单元区域.首先分析波矢K＝0.1时，它位于图形的左边.从图可以看出在采用AFEM后，低频的波包完全地进入了粗网格区域，而条件（1）的模拟方法，仍然有部分被返回.同时也发现引入低通滤波耗散方法后，对这个波矢影响很小.对于图形的右边波矢K＝1.0的模拟，如果不采用滤波方法，显然波完全被反射回细网格区域，而采用滤波方法后，这个反射波基本被消除了.因此，图5展示不同条件下的波包传播过程，证实AFEM加上低通滤波方法保证了K＝0.1波能传播到组单元区域，而过滤掉了K＝1.0的波包传播.

通过定义在细网格区域和粗网格区域间能量占有率，我们计算在某个波矢K下对应的反射系数和透射系数，结果如图6所示.从反射系数可以看出，如果不考虑低通滤波方法，由之前分析可知全反射发生位置大约在π／8处.所以很显然，发生全反射的波矢宽度远大于需要透射的波矢宽度.在AFEM下加入滤波耗散方法后，大部分的虚假反射波消除了.同时从透射系数可以看到，对低频传播影响很小.所以对整个Brillouin区计算得到的反射系数和透射系数，进一步证实我们设计的耗散方法具有低通滤波性质.虽然也看到在反射系数中K＝0.5的位置有稍强的反射，原因主要是选择的耗散参数β没有很好地被优化，这将是后续的工作.

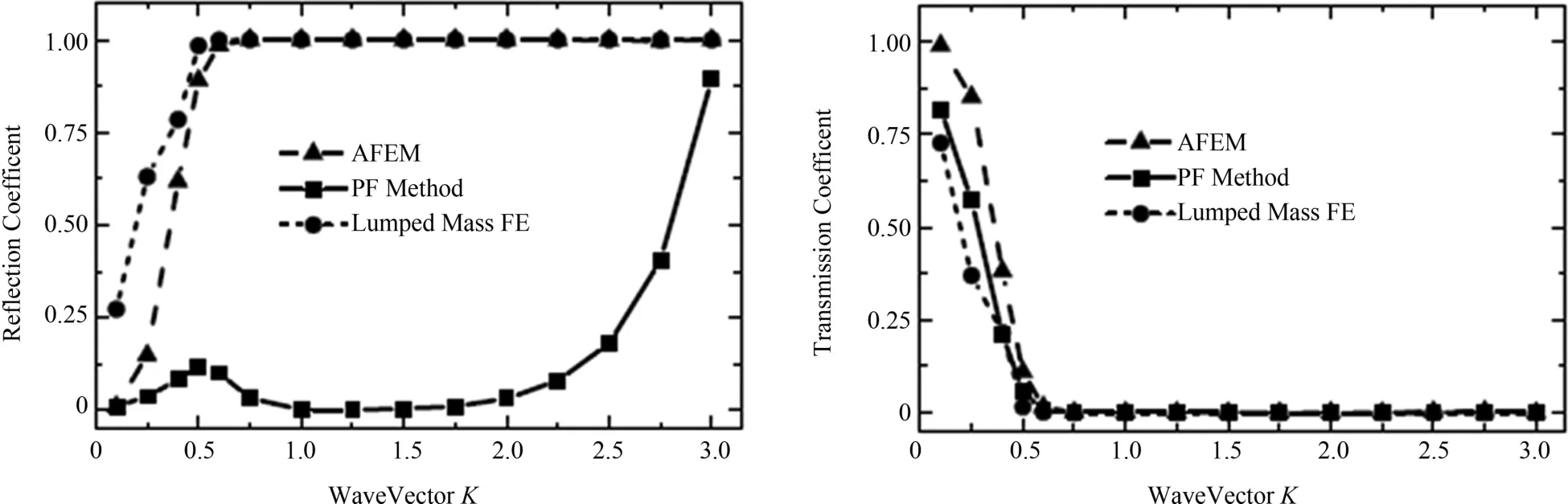
图6 三个不同模拟条件的反射系数和透射系数Fig.6 Reflection and transmission coefficients with three simulation conditions

5 结论

我们发展了一个基于原子尺度的有限元动力学方程.详细的理论推导给出一维情形下AFEM的质量矩阵和刚度矩阵具体形式，展示了其跨越从非局域的原子模型到局域的连续模型.比较其他物理模型，色散关系的计算证实AFEM拥有更多的振动频率，散射计算结果表明AFEM也具有更高的截止全反射波矢.但是由于单元增加造成的无法避免虚假波反射，引入了一种不同以往的耗散方法.这个耗散方法基于滤波器的原理，目的是为了消除高频的反射波，而不影响低频的透射波，从而保证粗单元区域具有低频的动力学行为.数值模拟不同波矢的传播特性，以及反射和透射系数的计算证实了低频滤波耗散方法有效地消除了大多数的反射波，而对低频波影响很小，同时在低频区域AFEM基本没有影响低频波的衰减.

原子尺度下的声子是应力波及热量传播的载体，分别对应于低频和高频振动模.宏观上则体现于连续力学本构关系和热传导方程.耦合原子和连续区域的模型后，为保证原子区域的物理信息能有效地传播到连续区域，原子区域的所有振动模需被分离为低频和高频.低频的振动模需要保证传播到连续区域体现力学特性而高频则需要被收集作为能量体现热传播.建立多尺度模型后，由于大网格的存在导致高频振动模被反射回原子区域，造成该区域局域温升，体系处于非热力学平衡.本工作的目的是消除高频振动模而不影响低频振动传播，这个思想在近来发展的热力学耦合多尺度方法可以看到［22］，本文的低通滤波耗散边界更容易实现.因此，我们发展的这个多尺度算法为发展热力学耦合的多尺度方法提供了一条新的途径.

［1］Miller R E，Tadmor E B.A unified framework and performance benchmark of fourteen multiscale atomistic／continuum coupling methods［J］.Modell Simul Mater Sci Eng，2009，17：1－51.

［2］Kohlhoff S，Gumbsch P，Fischmeister H F.Crack propagation in bcc crystals studied with a combined finite-element and atomistic model［J］.Phil Mag A，1991，64：851－878.

［3］Tadmor E B，Ortiz M，Phillips R.Quasicontinuum analysis of defecs in solids［J］.Phil Mag A，1996，73：1529－1563.

［4］Broughton J Q，Abraham F F，Bernstein N，Kaxiras E.Concurrent coupling of lengh scales：Methodology and application ［J］.Phys Rev B，1999，60：2391－1403.

［5］Rudd R E，Broughton J Q.Coarse-grained molecular dynamics：Nonlinear finite elements and finite temperature［J］.Phys Rev B，2005，72：144104.

［6］Wanger G J，Liu W K.Coupling of atomistic and continuum simulations using a bridging scale decomposition［J］.J Comp Phys，2003，190：249－274.

［7］Miller R，Tadmor E B，Phillips R，Ortiz M.Quasicontinuum simulation of fracture at the atomic scale［J］.Modelling Simul Mater Sci Eng，1998，6：607－638.

［8］Park H S，Liu W K.An introduction and tutorial on multiple-scale analysis in solids［J］.Comput Methods Appl Mech Eng，2004，193：1732－1772.

［9］Warner D H，Curtin W A，Qu S.Rate dependence of crack-tip processes predicts twinning trends in fcc metals［J］.Nature Mater，2007，6：876－881.

［10］Peng Q，Zhang X，Hung L，Carter E A，Lu G.Quantum simulation of materials at micro scales and beyond［J］.Phys Rev B，2008，78：054118.

［11］徐云，陈军，陈栋泉.加载条件微裂纹动力学行为的多尺度模拟［J］.北京理工大学学报，2010，30：357－360.

［12］邵宇飞，王绍青.基于准连续介质方法模拟纳米晶体Ni中裂纹的扩展［J］.物理学报，2010，59：7258－7265.

［13］Bazant Z P.Spurious reflection of elastic waves in nonuniform finite element grids［J］.Comput Meth In Appl Mech Eng，1978，16：91－100.

［14］Zhou S J，Lomdahl P S，Thomson R，Holian B L.Dynamic crack processes via molecular dynamics［J］.Phys Rev Lett，1996，76：2318－2321.

［15］Qu S，Shastry V，Curtin W A，Miller R E.A finite-temperature dynamic coupled atomistic／discrete dislocation method［J］. Modell Simul Mater Sci Eng，2005，13：1101－1118.

［16］Doll J D，Myers L E，Adelman S A.Generalized Langevin equation approach for atom／solid-surface scattering：Inelastic studies［J］.J Chem Phys，1975，63：4908－4914.

［17］Cai W，Koning M，Bulatov V V，Yip S.Minimizing boundary reflections in coupled-domain simulations［J］.Phys Rev Lett，2000，85：3213－3216.

［18］E W，Huang Z.Matching conditions in atomistic-continuum modeling of materials［J］.Phys Rev Lett，2001，87：135501.

［19］Yang J Z，Li X.Comparative study of boundary conditions for molecular dynamic simulations of solids at low temperature［J］. Phys Rev B，2006，73：224111.

［20］To A C，Li S.Perfectly matched multiscale simulations［J］.Phys Rev B，2005，72：035414－1－8.

［21］Jones R E，Kimmer C J.Efficient non-reflecting boundary condition constructed via optimization of damped layers［J］.Phys Rev B，2010，81：094301.

［22］Mathew N，Picu R C，Bloomfild M.Concurrent coupling of atomistic and continuum models at finite temperature［J］.Comput Methods Appl Mech Engrg，2011，200：765－773.

Low-pass Filter Boundary Condition for Atomic-based Finite Element Method

REN Guowu，TANG Tiegang，LI Qingzhong
（Institute of Fluid Physics，China Academy of Engineering Physics，Mianyang，Sichuan 621999，China）

An atomic-based finite element method is developed，spanning from atomic scale to macroscopic one.With theoretical deduction dispersion relation and dynamic scattering behavior are calculated.For spurious reflection caused by non-uniform grid，lowpass filter boundary condition is designed to effectively eliminate the reflection of high-frequency phonons，while keeping low-frequency ones transparent.These schemes are demonstrated with numerically calculating reflection and transmission coefficients in onedimensional modeling.

finite element；filter；reflection coefficient

date：2013－09－12；Revised date：2013－12－19

O242

A

2013－09－12；

2013－12－19

国家自然科学基金（11102191）及流体物理研究所发展基金（SFZ20120402）资助项目

任国武（1981－），男，助理研究员，主要从事材料力学计算研究，E-mail：guowu.ren＠gmail.com

1001-246X（2014）05-0514-09