多群辐射输运计算的输运综合加速方法
2014-06-09李双贵杭旭登
李双贵, 杨 容, 杭旭登,2
(1.北京应用物理与计算数学研究所,北京 100094;2.计算物理实验室,北京 100088)
多群辐射输运计算的输运综合加速方法
李双贵1, 杨 容1, 杭旭登1,2
(1.北京应用物理与计算数学研究所,北京 100094;2.计算物理实验室,北京 100088)
研究多群辐射输运计算的源迭代输运综合加速方法,通过优化灰体输运综合加速,构造了双层嵌套的输运综合加速方法.数值算例表明新方法较灰体输运综合加速进一步提高计算效率,且适用于吸收系数强间断的高维复杂几何问题.
多群辐射输运;离散纵标方法;源迭代;输运综合加速方法
0 引言
辐射输运是一种重要的能量传输机制,广泛存在于天体物理、惯性约束聚变,武器物理等诸多研究领域中[1-3].高温系统中,热物质不断发射光子,光子在传输过程中又被物质吸收从而加热物质,同时被加热的物质又发射更多的光子,实现辐射场与物质的能量交换.描述辐射输运过程的基本方程为光子输运方程(Boltzmann方程)和物质能量守恒方程[4].输运方程的确定论数值模拟中,离散纵标(简称SN)方法[5]是应用最为广泛的方法之一.由于SN方程的自变量多(空间三个,角方向二个,还有时间变量和能量变量),离散后得到的代数系统非常庞大复杂,研究其高效、快速求解算法[6-8]一直是相关研究领域的热点问题之一.为了避免代数矩阵的显式构造和直接求逆,SN方程通常采用源迭代算法求解.光性薄区域,源迭代算法快速收敛,简单有效.光性厚区域,辐射被物质反复吸收和再发射,源迭代算法很难收敛,计算费时,必须寻求快速收敛的迭代算法.
粒子输运理论中扩散综合加速方法[9](diffusion synthetic acceleration,DSA)是较为有效的一种源迭代加速方法.该算法利用源迭代过程中迭代解收敛最慢的部分具有弱的空间和角度依赖,通过求解源迭代误差方程的低阶扩散近似方程加速源迭代收敛.健壮而稳定的扩散综合加速方法要求低阶扩散算子的空间离散与高阶输运算子的空间离散相容(即加速方程的离散采用被加速方程的离散渐近极限形式),这使得DSA方法仅在一维和二维正交网格的数值模拟中能得到了很好的应用[9-11].在二维非正交网格上推导与输运算子空间离散相容的扩散方程离散格式相当困难,即便得到也形式复杂,编程实现繁琐,而且高维扩散方程离散后迭代求解也不容易,使得扩散综合加速方法的有效性难以保证.此外,Warsa等人[12]发现即便相容离散的扩散综合加速方法,在高维问题求解中也会由于吸收系数的强间断而失效.
输运综合加速方法[13-14](transport synthetic acceleration,TSA),由于其加速方程为低阶SN角度离散的输运方程,其空间离散与被加速方程的离散格式一致,不受空间离散相容性条件限制.此外,输运综合加速算法中加速方程仍为输运方程,数值求解可沿用被加速方程的程序模块,程序实现难度降低.利用源迭代误差方程的特点,设计快速收敛的输运综合加速方法,是提高复杂几何输运问题计算效率的有效途径之一.
将灰体输运综合加速(grey transport acceleration,GTA)方法[13]推广应用于加速二维柱几何任意四边形拉氏网格上多群辐射输运方程的源迭代求解,并对加速算法进行优化设计,进一步挖掘加速效率.利用TSA方法[14]对灰体输运方程的源迭代求解进行内层加速,设计了双重嵌套的输运综合加速算法,并进行数值例证,给出方法可行性结论.
1 辐射输运方程及其数值求解
假定辐射场非平衡,物质处于局部热动平衡状态,描述辐射输运问题的辐射输运方程和物质能量守恒方程为[4]

这里已对输运方程作多群处理,即把光子频率区间ν∈(0,∞)分为G个子区间(群):Δνg=(νg+1/2,νg-1/2),g=1,…,G.Ig为第g群光子的辐射强度,σg为群吸收系数,Ω为光子运动方向,r为空间变量,c为光速,B(T,ν)为Planck函数,Te为物质温度,ρ为物质密度,Cve为比热.
由于物质属性(这里指群吸收系数和比热)以及Planck函数都是关于物质温度大尺度变化的非线性函数,方程(1)和(2)为非线性强耦合方程组.数值求解方程(1-2)一般采用隐式时间差分格式,其向后欧拉时间离散格式分别为


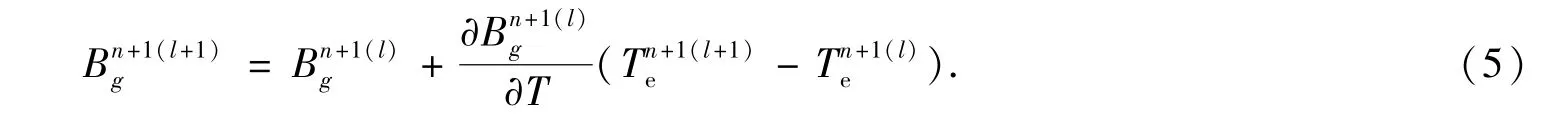
利用展开式(5),方程(4)可化为(为方便计,以下方程将略去时间上标n+1)

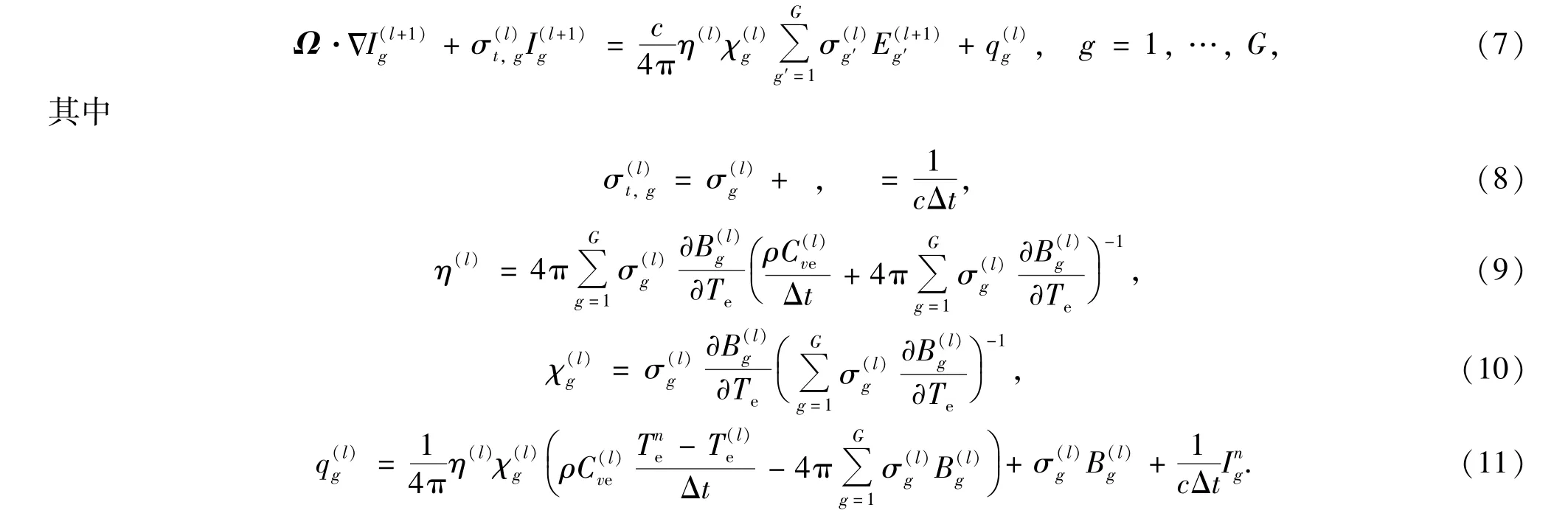
方程(7)与方程(3)比较,方程(3)的发射项(右端的第一项)已化为方程(7)的人为散射项(右端第一项)和源项q(l)g中的一部分.这样,问题(1)-(2)归结为迭代求解方程(7)和方程(6).
2 源迭代算法
源迭代算法应用于求解多群辐射输运方程(7).在每一Newton-Picard混合迭代步中,方程(7)是线性输运方程,为方便计略去非线性迭代上标后可写为

这里Ig为未知量,其余的量为已知量.由于方程(12)中群辐射强度通过发射项(右端第一项)相互耦合在一起,为了避免代数矩阵的显式构造和直接求逆,通常对方程(12)采用源迭代(source iteration,SI)求解(即通过迭代右端的耦合项,实现辐射强度在频率之间的耦合).方程(12)的源迭代算法具体描述为(k为源迭代指标)
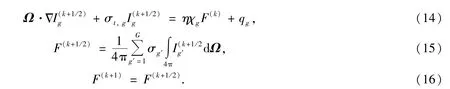
利用标准的Fourier分析源迭代算法的收敛效率.定义
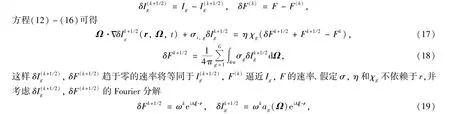
这里|ξ|=1,0<λ<∞.如果|ω|<1,|ω|最大的Fourier模以最慢的速度收敛于零,如果|ω|>1,则|ω|最大的Fourier模以最快的速度发散.将式(19)代入(17)、(18)可得
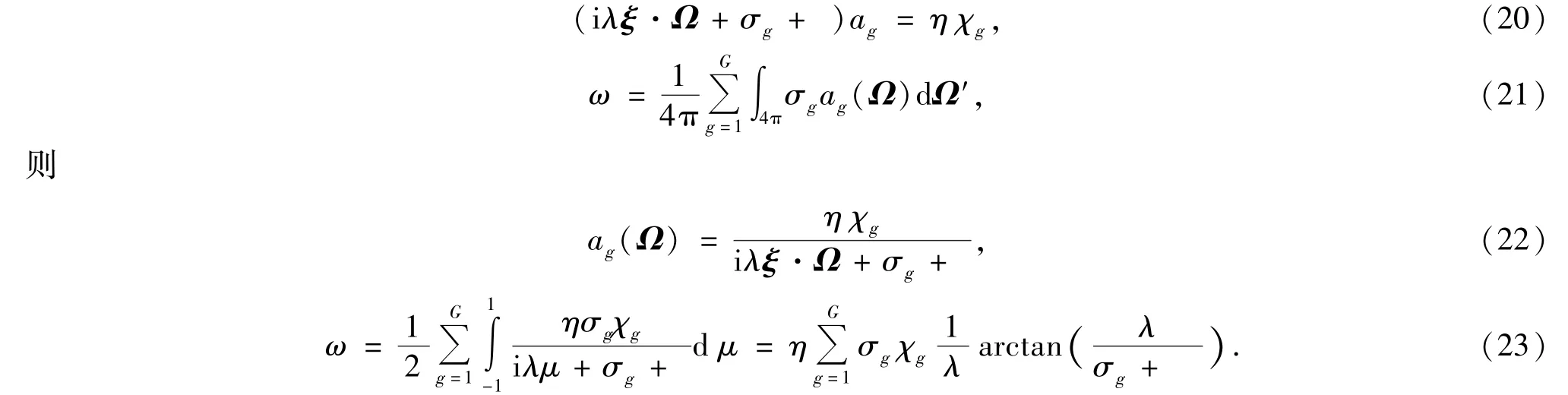
对任意给定频率分群g,式(23)中方括号内的项是λ的递减函数,在λ=0处取最大值.由此

ρL即为源迭代的谱半径,由上可知0<ρL<1,故源迭代是收敛的.但在高温光性厚介质区域σ很大,由(8)和(9)式可知η→1, /σg→0,则ρL→1,源迭代尽管收敛,但收敛很慢.降低谱半径ρL的最直接办法是取比较小的时间步长,由此计算步大大增加,导致误差累积,所以有必要寻求比源迭代方法收敛更快的迭代算法.
3 灰体输运综合加速
综合加速算法的基本思想是对源迭代误差方程进行恰当的近似,以近似方程的解修正源迭代解,达到加速的目的.上一节的分析已知当λ≈0时,ρL→1,取加速方程为误差方程在λ=0时的近似,即可捕捉源迭代过程中收敛最慢的解.利用方程(22)关于λ的展开式
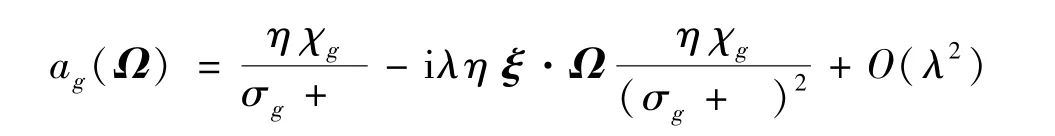
中λ→0时解的特征,Larsen[13]构造了源迭代算法(14)-(16)的灰体输运综合加速(GTA)

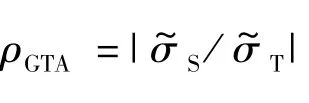

4 双层嵌套的输运综合加速
GTA算法(25)-(28)中,源迭代求解方程(27)的计算量较方程(25)已显著降低,这是因为方程(27)为单群方程且其谱半径ρGTA<ρL.但当σgΔt很大时,ρGTA→ρL→1.源迭代求解方程(27)至收敛需要的计算量增加,从而降低加速效率.双层嵌套输运综合加速方法是在GTA算法的基础上,进一步加速方程(27)的迭代求解,优化算法,提高整个算法的加速效率.
考察加速方程(27),其形式上相当于具有各项同性散射源项的单群线性中子输运方程,因此可以采用标准的源迭代加速方法对其源迭代求解进行加速.考虑到算法设计需要适应二维复杂几何应用问题以及降低程序实现的难度,借鉴Ramone和Adams[14]提出TSA方法对方程(27)进行加速.引入松弛因子β∈[0,1]构造(27)的加速方程,其散射截面为,为保持粒子守恒,总截面为

至此得到求解多群辐射输运方程(12)-(13)的双层嵌套输运综合加速算法


这里k为外层迭代指标,s为内层迭代指标,方程(33)的边界条件同(31).若方程(33)采用源迭代求解,其迭代收敛谱半径ρTSA为

方程(33)较方程(31)更容易迭代收敛.
双层嵌套输运综合加速算法(19)具有如下特点:
1)鉴于源迭代算法中收敛最慢的解与角度弱相关,加速方程(33)和(31)可以采用较方程(29)更低阶(S4或S2)的角度离散,从而减少计算量.
2)采用自适应策略.迭代过程中监测源迭代数值谱半径
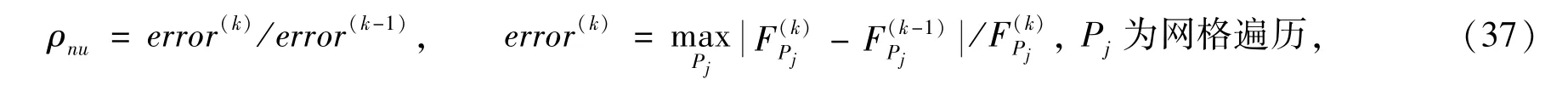
仅当谱半径大于某一给定值(~0.5)时根据需要启动加速方程(31)和(33)的求解,并对源迭代解进行修正.
3)方程(33)和(31)作为源迭代误差方程的近似并不要求精确求解,实际计算中可以结合问题特点通过选取参数β和适当调整迭代收敛标准,实现算法的最优化.
4)加速方程的求解可沿用求解输运方程(29)的程序模块,程序实现的复杂度大幅降低.
5)采用输运综合加速,避免了扩散综合加速算法稳定性条件对空间离散相容性条件的要求,适用于高维复杂几何问题.
6)SN输运方程若采用先进的预条件Krylov子空间方法求解,方程(31)和(33)仍可以作为预条件子加速其快速收敛.
5 数值结果
5.1 计算条件
算例为实际应用领域中的简化模型,考虑二维柱几何下的辐射传输计算.输运方程的空间离散均采用简单隅角平衡方法[15-16](适用于二维任意多边形凸网格),角度微分项由菱形差分近似,多群辐射输运方程(29)角度离散采用S8;光子频率分群为20群,辐射群吸收系数取自数据库[17];部分物性参数采用实际气体状态方程.
考察的算例中光厚介质为常密度Pb(ρ=10.5 g·cm-3),图1为辐射和电子温度为10 MK时,网格跨度约5×10-4μm时针对不同频率光子的光学厚度.由于不同频率的光子其自由程相差悬殊,以光子服从平衡谱(Planck谱)分布为例,对大部分光子而言网格的光学厚度约为10.随着温度的升高或降低,光子自由程也会有所增长或缩短.在本文所设计的算例中,光厚介质Pb的网格剖分对大部分光子而言总是光性厚的(光学厚度大于1).
为了有效避免假收敛(迭代算法收敛很慢,相邻两次迭代值相差很小,但远离收敛解,从而导致非物理解),多群辐射输运方程的源迭代收敛标准error(k)<ε中取ε=10-5.为提高算法计算效率,加速方程(31)和(33)都采用低阶角度离散(S2),在迭代计算中并不要求充分收敛,而是给定收敛标准ε=10-3或不超过最大允许迭代次数.这里我们定义加速方程(31)、(33)的最大允许迭代次数为NGTA、NTSA.在数值模拟中可采用参考经验值,单层GTA加速时取NGTA≈20,双层嵌套加速时取NGTA≈10,NTSA≈7.方程(33)中β取值为0.2.文献[16]已初步考察了GTA算法计算二维柱几何模型的加速效率(全过程计算相对于源迭代加速比约为6),由于在计算初始阶段时间步长很小,从而源迭代谱半径小收敛快,算法难以体现加速效果,反而增加了多余的计算量.本文考虑算法的自适应优化策略,仅当谱半径ρL大于某一给定值(≈0.5)时进行加速.这里单纯考察算法的加速效率,在物理时间10-4μs<t<5.0×10-4μs区间段(ρL>0.5),采用定步长Δt=5.0×10-6μs计算.
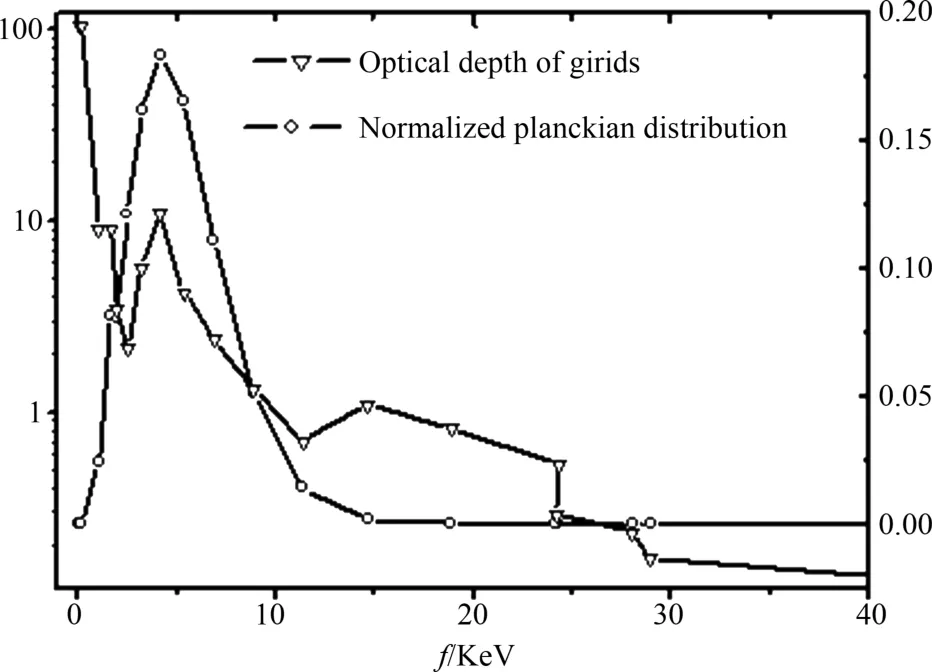
图1 网格的光学厚度(T=10 MK,ρ=10.5 g·cm-3)Fig.1 Optical depth of grids(T=10 MK,ρ=10.5 g·cm-3)
5.2 均匀介质算例
辐射在高Z介质Pb圆柱体内传输.圆柱半径为0.01 cm,高为0.01 cm,圆柱外表面均为自由面,圆柱体下底面Z=0处给辐射等效温度为11.6 MK的均匀恒温辐射源.整个区域分为20×20个四边形网格(见图2).

图2 20×20非矩形网格Fig.2 20×20 quadrilateral grids

图3 源迭代的理论谱半径和数值谱半径(算例1)Fig.3 Theoretic and numerical spectral radius of SI(Example 1)
在光性厚的介质中,辐射被物质反复吸收和再发射,反映到数值计算中源迭代算法收敛谱半径趋于1,迭代很难收敛.图3为源迭代算法的理论谱半径(式(24))和数值谱半径(式(37)),二者非常接近(≈0.98),数值谱半径略低于理论谱半径,理论公式很好地反映源迭代算法的收敛状态.图4为未加速和加速算法迭代求解方程(12)-(13)的数值谱半径,GTA加速算法和双重嵌套加速算法中数值谱半径较简单源迭代算法明显缩小,分别由0.98缩小至0.4和0.2左右.迭代收敛所需求解多群输运方程的平均次数由192.5次降为12次和5次(见表1).尽管迭代过程中增加了两个单群输运方程(31)和(33)的计算,但增加的计算量远小于提高收敛速度所减少的计算量,凸显其加速效率:完成计算源迭代需要76.25分钟,单层GTA算法需5.25分钟,而双层嵌套加速仅需3.08分钟,较源迭代算法获得了24倍的加速.图5为t=5.0×10-4μs时,不同迭代算法求解得到的辐射温度分布,计算结果完全吻合,证明双层嵌套的加速算法提高了计算效率,但不改变数值解.
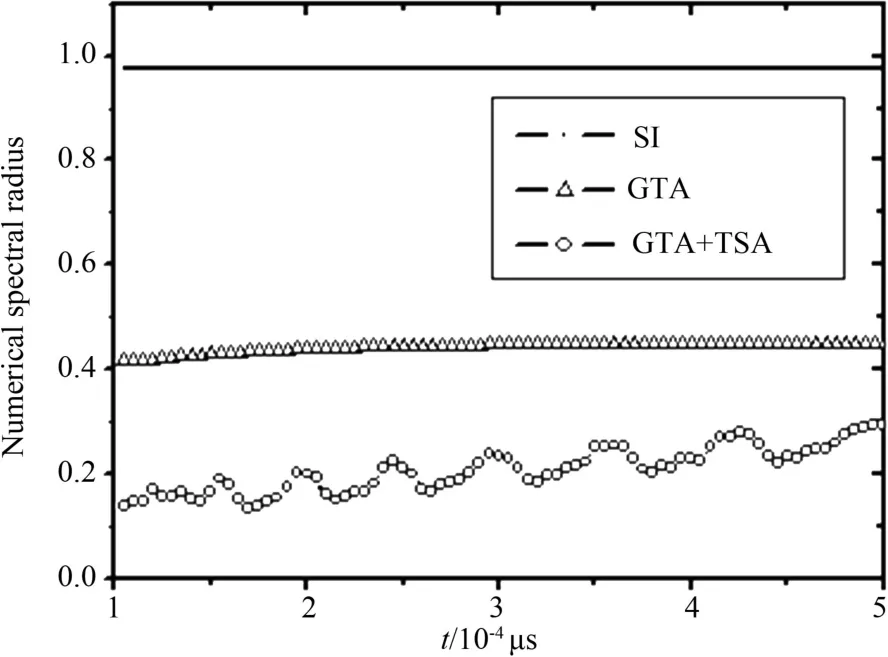
图4 加速和未加速算法的数值谱半径(算例1)Fig.4 Numerical spectral radius of unaccelerated and acclelerated algorithms(Example 1)
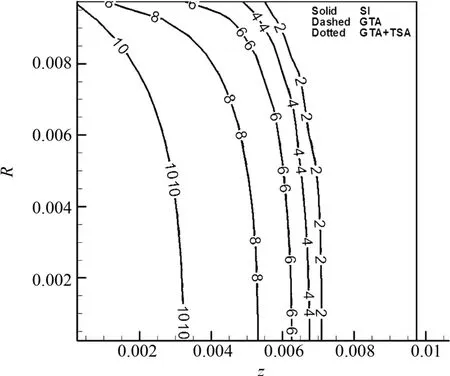
图5 加速和未加速算法的辐射温度分布(算例1)Fig.5 Radiative temperature snapshot of unaccelerated and acclerated algorithms(Example 1)
5.3 吸收系数强间断的多介质算例
鉴于Warsa等人[12]发现即便相容离散的扩散综合加速方法,在高维计算中也会由于吸收系数的强间断而失效,故有必要考察加速算法求解吸收系数强间断问题的有效性.
辐射在填充CH介质的Pb管中传输.圆柱半径为0.28 cm,高为1 cm,半径为0.25 cm以内的中心区域为低密度的CH介质(ρ=0.05 g·cm-3).四边形网格剖分(CH区域:20×5,Pb介质区:20×30).圆柱外表面均为自由面,圆柱体下底面Z=0处半径为0.25 cm的中心区域给辐射等效温度为20.0 MK的均匀恒温辐射源.
GTA算法和双重嵌套加速算法的数值谱半径约为0.4和0.2(见图6),平均迭代次数由源迭代算法所需的277.6次分别降为14次和7.2次(见表2),获得约17倍和27倍的加速比,加速算法保持了稳定的加速效率.t=5.0×10-4μs时,考察光薄的CH泡沫中辐射温度和电子温度的轴向分布,图7表明不同迭代算法求解得到计算结果吻合很好,数值解稳定.辐射从输运管右端逃逸前在CH泡沫中的谱分布与Planck谱存在偏离(见图8),可见辐射并没有达到平衡状态.图7和图8表明算例中辐射与物质、辐射自身都未能达到平衡状态,也论证了采用多群输运建模的必要性.
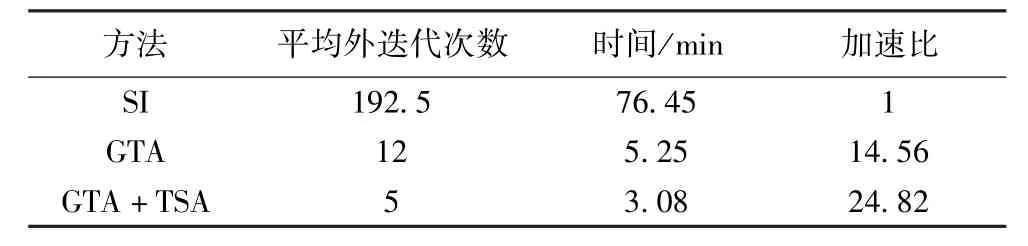
表1 加速和未加速算法的计算结果比较(算例1)Table 1 Computational comparison of unaccelerated and acclelerated algorithms(Example 1)

表2 加速和未加速算法的计算结果比较(算例2)Table 2 Computational comparison of unaccelerated and acclelerated algorithms(Example 2)

图6 加速和未加速算法的数值谱半径(算例2)Fig.6 Numerical spectral radius of unaccelerated and acclelerated algorithms(Example 2)
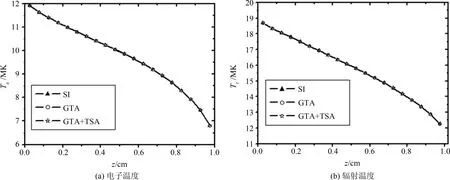
图7 CH介质中沿Z轴的温度分布(左:电子温度;右:辐射温度)Fig.7 Snapshots of temperature along Z axial in CH medium(left:material temperature,right:radiation temperature)
6 结论
将灰体输运综合加速应用于加速二维柱几何多群辐射输运方程的源迭代求解,采用TSA方法加速灰体输运方程的迭代求解,设计了双重嵌套的输运综合加速方法.数值算例表明:在高温光性厚区域多群辐射输运计算中源迭代算法收敛谱半径接近1,GTA方法能较源迭代方法获得15倍左右的加速比,双重嵌套输运综合加速方法获得了25倍左右的加速比(较单层GTA方法提高了约40%的计算效率).算法适用于非规则网格的多维问题,且在吸收系数强间断的多介质问题中保持了稳定的加速效率.

图8 输运管右端CH泡沫的辐射谱分布Fig.8 Spectrum of radiation energy in CH foam before leaking from transport pipe
[1]Bowers R L,Wilson J R.Numerical modeling in applied physics and astrophysics[M].Boston:Jones and Bartlerr Publishers,1991.
[2]Pei W B.The contruction of simulation algorithms for laser fusion[J].Commun Comput Phys,2007,2:255-270.
[3]Tian Zhou,Guo Yonghui,Qiao Dengjiang.Two-dimensional numerical simulation of radiation hydrodynamics in underground strong explosions[J].Chinese Journal of Computational Physics,2012,29(3):361-368.
[4]Pomraning G C.The equations of radiation hydrodynamics[M].New York:Pergamon Press,1973.
[5]Lewis E E,Miller W R.Computational methods of neutron transport[M].New York:John Wiley&Sons,1984.
[6]Turchsin B,Ragusa J C,Morel J E.Angular multigrid preconditioner for Krylov-based solution techniques applied to the Snequations with highly forward-peaked scattering[J].Transport Theory and Statistical Physics,2012,41:1-22.
[7]Morel J E,Yang T Y B,Warsa J S.Linear multifrequency-grey acceleration recast for preconditioned Krylov iterations[J]. Journal of Comput Phys,2007,227:244-263.
[8]Wei Junxia,Yuan Guangwei,Yang Shulin,Shen Weidong.A parallel algorithm with interface prediction and correction for time-dependent transport equation in 2D cylindrical geometry[J].Chinese Journal of Computational Physics,2012,29(2):198-204.
[9]Adams M L.Fast iterative methods for discrete-ordinates particle transport calculation[J].Progress in Nuclear Energy,2002,40:3-159.
[10]Morel J E,Wareing T A,Smith Kenneth.A linear-discontinuous spatial differencing scheme for SNradiative transfer calculations[J].Journal of Comput Phys,1996,128:445-461.
[11]Li Shuanggui,Feng Tinggui.Diffusion-synthetic acceleration method for diamond-differenced discrete-ordinates radiative transfer equations[J].Chinese J Comput Phys,2008,25(1):1-6.
[12]Warsa J S,Wareing T A,Morel J E.Krylov iterative methods and the degraded effectiveness of diffusion synthetic acceleration for multidimensional SNcalculation problems with material discontinuities[J].Nucl Sci Eng,2004,147:218-241.
[13]Larsen E.A grey transport acceleration method for time-dependent radiative transfer problems[J].J Comp Phys,1988,78:459-480.
[14]Ramone G L,Adams M L and Nowak P F.A transport synthetic acceleration method for transport iteration[J].Nul Sci Eng,1997,125:257-283.
[15]Adams M L.Subcell-balance methods for radiative transfer on arbitrary grids[J].Transport Theory and Statistical Physics,1997,26(4):385-432.
[16]Li Shuanggui,Hang Xudeng,Li Jinghong.Calculations of two dimensional strong-coupled radiative transfer problems[J]. Chinese J Comput Phys,2009,26(2):247-253.
[17]Xu Yan,Lai Dongxian,Feng Tinggui.Establishment of multi-groups atomic parametric database[J].High Power Laser and Particle Beams,1997,9(4):533-537.
Transport Synthetic Acceleration Methods for Multi-group Radiative Transfer Calculations
LI Shuanggui1,YANG Rong1,HANG Xudeng1,2
(1.Institute of Applied Physics and Computational Mathematics,Beijing 100094,China;2.Laboratory of Computational Physics,Beijing 100088,China)
Convergence of source iteration is analyzed for multi-group radiative transfer calculations.A two-level nesting transport acceleration method is developed.Numerical results show speedup factors of the scheme are higher than that of GTA method.The scheme is feasible for non-rectangle grid calculations of 2D problems with large discontinuities of material properties.
multi-group radiative transfer;discrete ordinate method;source iteration;transport synthetic acceleration
date:2013-09-10;Revised date:2014-01-30
O434.11
A
2013-09-10;
2014-01-30
国防基础科研计划(B1520110011)、国家自然科学基金(91130002)和国家863高技术惯性约束聚变专题资助项目
李双贵(1976-),女,湖南衡东,博士,副研究员,从事辐射输运计算方法与数值模拟研究,E-mail:lishg@iapcm.ac.cn
1001-246X(2014)05-0505-09
