降雨入渗过程中土质边坡稳定性计算

邢小弟，张 磊，谈叶飞，邱城春，谢兴华

(1.南京水利科学研究院 交通运输部通航建筑物建设技术行业重点实验室，江苏 南京 210029；2.河海大学 水利水电学院，江苏 南京 210098；3.山东黄河河务局，山东 济南 250011；4.青海玉能电力开发有限公司，青海 西宁 810007）

降雨入渗过程中土质边坡稳定性计算

邢小弟1，2，张 磊3，谈叶飞1，邱城春4，谢兴华1

(1.南京水利科学研究院 交通运输部通航建筑物建设技术行业重点实验室，江苏 南京 210029；2.河海大学 水利水电学院，江苏 南京 210098；3.山东黄河河务局，山东 济南 250011；4.青海玉能电力开发有限公司，青海 西宁 810007）

在室内试验资料基础上，提出了土体抗剪强度与降雨入渗时间以及土体含水率的函数关系，修正了考虑土条间相互作用力的简化毕肖普方法，使之能够体现边坡土体含水率变化引起的土体强度降低现象。采用Fortran语言设计平台，开发了耦合饱和-非饱和渗流有限元计算与边坡稳定极限平衡方法(修正的简化Bishop方法）的计算程序，考虑边坡土体抗剪强度参数随着降雨入渗发展、含水率变化而变化，采用饱和-非饱和渗流计算降雨期间边坡土体含水量变化以及扩展过程。计算了物理试验模型在降雨条件下，土坡内部渗流发展过程，以及边坡安全度的变化情况。计算结果与试验结果吻合，与修正前简化Bishop方法计算得到的边坡安全系数相差35%左右。本文提出的计算方法为降雨诱发土质滑坡研究提供了一种新的可供参考的定量分析方法。

降雨入渗；抗剪强度；压力水头；边坡稳定性

滑坡在我国地质灾害中占很大比重［1］。降雨是引发边坡失稳的重要因素［2-4］，因此研究降雨过程中边坡安全系数计算方法具有重要的现实意义。国内有关边坡稳定计算的规范多推荐传统的极限平衡分析法，极限平衡分析法采用饱和土体有效应力计算土坡的安全系数。在计算降雨情况下的边坡稳定性时，主要考虑由降雨入渗引起坡体内部浸润面抬高，含水土体重度增加而导致土条下滑力增加，并未考虑由此导致的土体抗剪参数的降低。忽略这一因素，将使计算得到的安全系数偏高，不利于合理评价边坡安全性［5-6］。本文依据室内试验资料，提出了土体抗剪强度参数与含水率变化的函数关系，修正简化Bishop方法，在Fortran语言平台上，开发了饱和-非饱和渗流与边坡稳定性计算相结合的计算模型。其中饱和-非饱和渗流模型采用文献［7］改进的饱和-非饱和渗流有限元计算方法，研究边坡安全系数随降雨入渗的变化过程以及边坡滑裂面的位置变化。

1 土体抗剪强度随降雨入渗变化规律

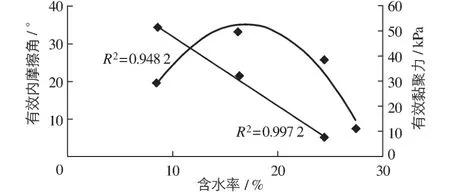
图1 含水率与有效内摩擦角和有效黏聚力的关系Fig.1 Relationship curves of moisture content-effective internal friction angle and moisture contenteffective cohesion

由于模型边坡为重塑土按照一定干密度经过压实而成，根据土体的实际状态，选取模型边坡土样，在保证干密度相同的条件下，将水均匀地喷洒在烘干的土体上并搅拌均匀，配置后的土样放置在密封容器内24 h使水分均匀分布。测得4组不同含水率，每组包含4个试样，利用三轴剪切渗透试验仪按照不固结不排水方法测定土样的抗剪强度参数，得到不同含水率下土体的应力应变关系。在τf-σ平面内绘制强度包线，得到土体的强度参数与含水率关系(见图1），并进行曲线拟合［8］。由图1可见，有效内摩擦角与含水率成线性关系，随着含水率的增加，有效内摩擦角减小；有效黏聚力先随含水率增加而增大，在含水率达到17%时，达到最大值，然后随之减小。

式中：ω为土体质量含水量；C′为土体有效黏聚力；φ′为土体有效内摩擦角，当土体饱和时，φ′=2.5°，土体含水量为37.5%时，φ′=4.52°，当37.5%＜ω＜40%时，φ′按插值法取值，当ω为其他取值时，按式(1）计算。

2 计算模型基本原理

2.1 简化Bishop计算方法修正

简化毕肖普安全系数公式［9］为：

考虑降雨入渗时，非饱和土采用Fredlund双应力变量强度公式［10］，饱和土采用库伦强度准则，简化毕肖普安全系数公式为：

传统计算时，有效内摩擦角及有效黏聚力均是常数，这与实际情况不符，根据本文试验可知，抗剪强度参数与土体含水率存在一定关系，将式(1），(2）代入式(4）可得

式中：Fs为边坡安全系数；Wi为土条重力；b为土条宽度；θ为土体体积含水率；θr为土体残余含水率；θs为土体饱和含水率；τf为土体破坏时的剪应力；c′为土体有效黏聚力；φ为土体有效内摩擦角；σ为土体破坏时滑面上的法向总应力；ua为孔隙气压力；uw为孔隙水压力；(σ-ua）为土体破坏时滑面上的净法向应力；(uauw）为土体的基质吸力；mai中包含安全系数Fs，因此要通过迭代求解计算确定。

2.2 渗流计算原理

根据质量守恒原理及表示各向异性的达西定律，则各向异性饱和-非饱和渗流方程可表示为：

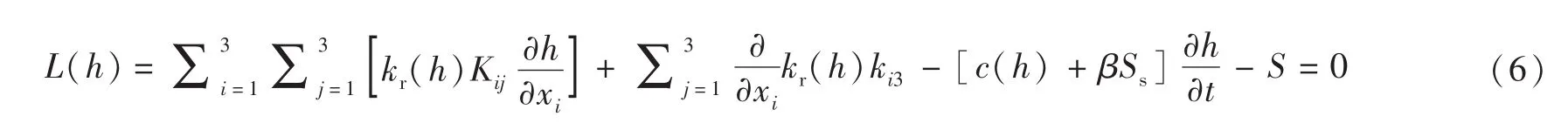
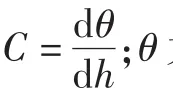
边坡表面即为降雨入渗边界，当其孔隙水压力小于零时为流量边界，否则为零压力水头边界。土中的初始压力水头值是在未考虑降雨条件下计算的初始含水率下边坡的稳定渗流情况所对应的孔隙水压力分布。土体的非饱和渗透系数可以采用土-水特征曲线或者是根据VG模型推求得到。

3 算例验证

试验边坡采用张磊［11］等人设计的室内人工降雨边坡模型，降雨强度为50 mm/h，坡比为1：1.5，边坡长50 cm，高33.4 cm。试验前制备所需土样，采用分层击实法制造边坡模型，利用孔隙水、含水率传感器监测降雨下边坡土体内的含水率及孔隙水压力的变化情况，直线位移传感器量测边坡局部表面的滑动位移，雾化喷头控制降雨强度。

计算使用上述试验边坡，几何特性及渗流边界如图2所示。该土的饱和渗透系数为7.488×10-5m/s，初始质量含水率为6.5%。非饱和水力参数采用试验获得的土-水关系曲线(图3）。由于测得的饱和含水率是土壤抽气饱和后的饱和含水率，而在降雨试验中，土体难以达到完全饱和状态，故计算时选取降雨试验达到的饱和含水率。图中测点A，B及测点1～3为研究辅助截面上的特征点。

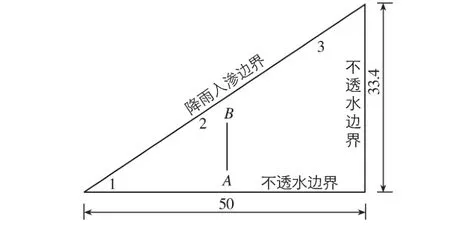
图2 边坡几何特性及渗流边界(单位：cm）Fig.2 Slope model and seepage boundary(unit：cm）

图3 土水特征曲线Fig.3 Soil-water characteristic curve

图4是各特征点含水率变化趋势。由图可见特征点在降雨持续2 h后都达到饱和状态，坡脚处测点1最早达到饱和，点A晚于点B含水率显著升高。

图4 各特征点含水率变化Fig.4 Variations of water content of measuring points

由此推论：在均匀降雨条件下，随着雨水入渗，高程较高点处的雨水在进入土体之后，由于重力作用，逐渐向高程较低处移动，导致靠近边坡坡脚处点的含水率增长迅速，坡脚处先趋于饱和。测点1～3含水率开始变化时间和含水率峰值接近，故选取测点2和A，B进行比较，计算和试验得到的最大含水率相对误差分别为11%，0和17%，含水率开始变化时间相对误差分别为0，20%和0。可见，各测点在含水率峰值及含水率开始变化时间上的最大相对误差是20%，计算精度符合要求；各测点试验值与计算结果在变化趋势上互相吻合。

由于试验中采集压力水头的仪器不能量测负压力水头，而在计算时由于已知土体含水量，根据土-水压力曲线计算的压力水头值作为渗流计算的初始压力水头。图5为各测点压力水头变化趋势。可见，计算边坡在降雨入渗过程中孔隙水压力与试验结果的变化趋势一致；测点1的孔隙水压力启动早且变化快，该点位于边坡坡脚，位置最低；在同一时刻，沿坡脚向上特征点的孔隙水压力减小，且随着高程的增加，达到相同的孔隙水压力所需时间增加，这是由于在降雨过程中，雨水在边坡表面入渗后逐渐向坡脚处渗流，使得坡脚处的孔隙水压力先增大。试验中由于边坡表面排水不通畅，导致试验值偏大。

图5 各测点压力水头变化Fig.5 Variation of pressure heads of measuring points

依据上述渗流计算的暂态含水量及压力水头，分别采用修正前后的Bishop方法计算不同时刻下边坡的安全系数值(图6），得出在降雨历时2.3 h时，边坡最小安全系数的滑面是以(X，Y）=(18，30）为圆心，R= 19 cm为半径的圆弧(图7）。

图6 圆弧边坡的安全系数变化趋势Fig.6 Variation of safety coefficients of the arc slope

图7 试验降雨2.3 h边坡滑面位置Fig.7 Position of slope slip in 2.3 h rainfall tests

本文方法计算得该圆弧的安全系数随着雨水入渗一直降低直到趋于稳定值，2.3 h时为0.963。表明降雨开始时，由于雨水的入渗，土体含水率慢慢增大，基质吸力下降，边坡的安全系数迅速降低，土体在趋于饱和时，边坡安全系数缓慢降低，说明基质吸力对于边坡稳定安全具有重要作用；修正前计算的该圆弧在2.3 h的安全系数为1.501，在降雨过程中其安全系数随着降雨的持续一直降低且数值比本文方法偏大，说明修正后的计算模型与实际情况更加相符。

4 结 语

(1）在总结物理试验的基础上提出了边坡土体抗剪强度参数随含水率变化的经验计算式，随着降雨的持续，边坡土体含水率增加，基质吸力降低，土体抗剪强度也随之降低，从而使边坡处于不稳定状态。

(2）将饱和-非饱和渗流程序与修正后的简化Bishop方法结合在一起，在Fortran语言平台上编制了利用修正后的简化Bishop方法计算降雨下的边坡稳定程序。经试验模型验证，该方法符合实际情况，可用于计算降雨下的边坡安全系数及其滑面位置。

(3）在相同的计算条件下，修正后的简化Bishop方法对应的边坡安全系数小于修正前的相应值；随着降雨的持续，修正前的安全系数一直降低，修正后的安全系数在非饱和时降低很快，之后趋于稳定。

本文研究对象为重塑砂土，由于天然土体性质十分复杂，不同种类土样的抗剪强度与含水率所对应的函数关系可能不同，其规律有待进一步研究。

［1］中华人民共和国国土资源部.2012中国国土资源公报［M］.北京：中华人民共和国国土资源部，2013.(Ministry of Land and Resources of the People′s Republic of China.China land and resources communique in 2012［M］.Beijing：Ministry of Land and Resources of the People′s Republic of China，2013.(in Chinese））

［2］郑明新，王全才.降雨滑坡的时空预测新方法［J］.中国地质灾害与防治学报，1997，8(3）：45-49.(ZHENG Min-xin，WANG Quan-cai.A new method about time and space predication of rainy landslides［J］.Chinese Journal of Geological Hazards and Control，1997，8(3）：45-49.(in Chinese））

［3］钟荫乾.滑坡与降雨关系及其预报［J］.中国地质灾害与防治学报，1998，9(4）：81-86.(ZHONG Yin-qian.Landslide related to rainfall and it′s forecasting［J］.Chinese Journal of Geological Hazzards and Control，1998，9(4）：81-86.(in Chinese））

［4］殷坤龙，韩再生，李志中.国际滑坡研究的新进展［J］.水文地质工程地质，2000，27(5）：1-4.(YIN Kun-long，HAN Zai-sheng，LI Zhi-zhong.Progress of landslide researches in the world［J］.Hydrogeology and Engineering Geology，2000，27 (5）：1-4.(in Chinese））

［5］PETERS R R，KLAVETTER E A.A continuum model for water movement in an unsaturated fractured rock mass［J］.Water Resources Research，1988，24(3）：416-430.

［6］TSAPARAS I，RAHARDJO H，TOLL D G，et al.Controlling parameters for rainfall-induced landslides［J］.Computers and Geotechnics，2002，29(1）：1-27.

［7］胡云进.裂隙非饱和渗流试验研究及有地表入渗的裂隙岩体渗流数值分析［D］.南京：河海大学，2001.(HU Yun-jin. Testing study on unsaturated seepage in fracture and numerical analysis on seepage in fracture rock mass due to surface infiltration［D］.Nanjing：Hohai University，2001.(in Chinese））

［8］张磊.含水率变化对边坡稳定影响试验研究［D］.南京：河海大学，2012.(ZHANG Lei.Experimental study on the changes of water content influence on slope stability［D］.Nanjing：Hohai University，2012.(in Chinese））

［9］殷宗泽，钱家欢.土工原理与计算［M］.北京：商务印书馆，1981：587.(YIN Zong-ze，QIAN Jia-huan.Geotechnical principles and calculation［M］.Beijing：Commercial Press，1981：587.(in Chinese））

［10］FREDLUND D G，RAHARDJO H.Soil mechanics for unsaturated soils［M］.New York：Wiley and Sons Inc，1993.

［11］张磊，郭海庆，谢兴华，等.人工降雨入渗边坡破坏试验研究［J］.水利水运工程学报，2013(6）：21-27.(ZHANG Lei，GUO Hai-qin，XIE Xing-hua，et al.Experimental study on artificial rainfall infiltration into slope［J］.Hydro-Science and Engineering，2013(6）：21-27.(in Chinese））

Calculation method for soil slope stability under the action of precipitation infiltration

XING Xiao-di1，2，ZHANG Lei3，TAN Ye-fei1，QIU Cheng-chun4，XIE Xing-hua1
(1.Key Laboratory of Naυigation Structure Construction Technology，MoT，Nanjing Hydraulic Research Institute，Nanjing 210029，China；2.College of Water Conserυancy and HydropoWer，Hohai Uniυersity，Nanjing 210098，China；3.YelloW Riυer Shandong Bureau，Jinan 250011，China；4.Qinghai Yushu Electric PoWer Deυelopment Co.，Ltd.，Xining 810007，China）

Based on the model test data，presenting the soil shear strength parameters and precipitation infiltration time as a function of the moisture content，modifying the simplified Bishop calculation model make it being able to reflect the phenomenon that the strength of the soil mass would be reduced by the change in the moisture content of the slope soil mass.With the aid of Fortran program，a program which is coupling saturated-unsaturated seepage finite element method and limit equilibrium slope stability(a corrected simplified Bishop method）is developed in this study.The program takes into account the slope soil shear strength parameters changed along with the development of precipitation infiltration，using saturated-unsaturated seepage for calculating variation and expansion process of the moisture content of the slope soil mass during rainfall.Through physical model tests，slope seepage in the development process and the process of change in the slope safety degree under the rainfall conditions have been calculated and analyzed.And the calculated results are good in agreement with the experimental research results，which differs by about 35%from the slope safety factor given by the simplified Bishop method before correction.This corrected simplified calculation method for slope stability will provide a new useful reference for the calculation of precipitation-induced landslides.

precipitation infiltration；shear strength；pressure head；slope stability

P642.22 文献标心码：A

1009-640X(2014）03-0098-06

2013-12-23

邢小弟(1986-），女，河北保定人，硕士研究生，主要从事渗流水力学研究。E-mail：nhrixx@163.com