基于FLUENT的库区涌浪数值模拟

邓成进，袁秋霜，侯延华，贾 巍

(中国水电顾问集团西北勘测设计研究院有限公司，陕西 西安 710065）

基于FLUENT的库区涌浪数值模拟

邓成进，袁秋霜，侯延华，贾 巍

(中国水电顾问集团西北勘测设计研究院有限公司，陕西 西安 710065）

基于流体计算软件FLUENT，模拟某水电站库区近坝变形体可能失稳后下滑引起库区水面变化过程，分析初始涌浪形成以及涌浪在对岸爬坡和涌浪沿岸传播的过程；研究挡水建筑物对库区涌浪沿岸传播的影响，得出初始涌浪高度，以及对岸、沿岸、坝址处的最大浪高，并与潘家铮法估算结果进行对比分析。分析结果表明，数值模拟能较好反映波浪爬坡和沿岸传播过程，真实模拟库区水体相互作用；由于库区涌浪运动受大坝建筑物阻挡作用，库区水面的反复震荡和涌浪叠加，会形成更高的涌浪。计算的初始涌浪及库区各处的最大涌高更符合实际情况，可为近坝库区的工程设计及涌浪灾害的预防提供参考。

库区；滑坡体；爬坡过程；最大浪高；涌浪叠加；挡水建筑物；数值模拟

库区存在的滑坡、崩滑体等不良地质体在失稳后高速滑入库中，产生的高速波浪足以对沿岸及下游建筑物和居民生命财产构成巨大威胁。1963年发生在意大利瓦依昂水库的滑坡［1］、1982年发生的鸡扒子滑坡、1985年发生的新滩滑坡［2］、2003年发生的千将坪滑坡等库区滑坡失稳后激起的巨大涌浪，均造成了巨大的人员伤亡和财产损失。因此，研究库区滑坡涌浪受到国内外学者的广泛关注。但是，由于库区涌浪受多种因素影响且十分复杂，涌浪形成的边界条件和初始条件难以明确定义，滑坡涌浪的计算还没有一种通用的方法。目前，研究库区滑坡涌浪的手段主要有物理试验、经验计算公式和数值模拟等［3-5］。其中，经验公式法主要有：Noda法、潘家铮法、中国水利水电科学研究院经验公式法、美国土木工程学会法、Slinger-land& Voight公式等。物理模型试验也取得一定的经验，殷坤龙等［6］采用物理试验方法研究了三峡水库库岸滑坡问题。随着计算机及数值理论的迅速发展，采用FVM，FEM，VOF等方法能较好地模拟流体飞溅、融合等复杂自由表面现象，因此，基于流体力学的涌浪数值模拟有了一定程度的研究［7-9］。然而，现有数值模拟方面的研究主要集中在模拟滑块垂直入小水槽内，而对在宽广水域中的涌浪问题研究较为欠缺，也很少有尝试通过数值模拟研究挡水大坝对库区涌浪传播的影响。

本文采用FLUENT软件建立某库区近坝库岸变形体失稳后产生涌浪的数值模型，模拟滑体滑动后库区涌浪形成及传播的过程；计算分析了大坝对库区涌浪传播过程的影响，得出初始涌浪高度、涌浪沿岸的传播高度以及涌浪到达大坝时的爬坡高度，并将其结果与潘家铮法估算的涌浪高度进行对比分析，为工程设计提供参考。

1 基于FLUENT软件的数值模拟方法

FLUENT软件是一种基于有限体积法发展起来的通用商业流体计算动力学软件包，用于模拟从不可压缩到高度可压缩范围内的复杂流体运动，在水工泄水建筑物水力学计算方面应用广泛。

1.1 控制方程

对于二维的瞬态流，其基本控制方程包括：连续性方程和以速度和压力为变量的动量守恒方程。

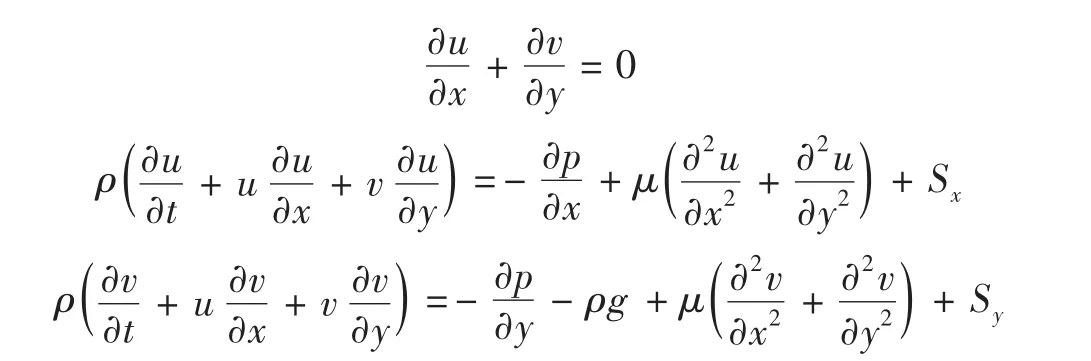
式中：ρ为流体密度；u和υ分别为流体在x和y方向的速度分量；μ为动力黏性系数；Sx和Sy分别为x和y方向附加动量源项。

1.2 体积分数方程

FLUENT软件采用VOF(Volume of Fluid）方法追踪自由面，VOF方法能很方便地处理自由面大变形和自由面拓扑结构发生变化等复杂情况。在VOF方法中，引入了体积分数aq的概念，用于定义单元内第q相流体所占体积与单元体积的比值。aq=0表示q相物质为空；aq=1则代表q相物质充满；0＜aq＜1，则表示该单元为交接面单元。水库水面的波浪流动属于水气分层两相流，aq满足方程：

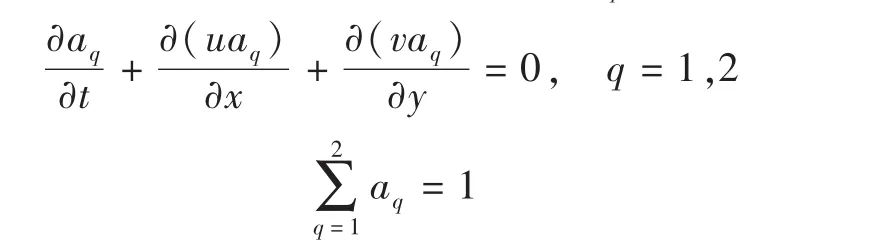
1.3 数值求解方法

利用有限体积法(FVM）建立离散方程，从而进行数值计算。本文控制方程中的扩散项采用中心差分格式，对流项采用如下离散格式：压力方程选用Body Force Weighted格式，体积分数选用几何重构法，动量方程、湍动能方程和湍流耗散率方程则选用二阶迎风格式。FLUENT软件进行求解的过程中，有3种压力-速度耦合方式可供选择，分别为SIMPLE，SIMPLEC和PISO。本文离散方程的数值求解采用速度压力耦合的PISO算法。

1.4 动网格技术

在FLUENT软件中，动网格技术主要用于处理由于流域边界运动而引起的流域特征，包括流域形状、速度、压力等改变的流动问题。流体边界的运动引起网格的拉伸和变形，每一时间步的网格更新需根据新的边界条件位置得出。FLUENT软件提供了3种变形区域内的网格更新方法，包括基于弹性变形的网格更新法、动态网格层变法和局部网格重构法。

2 涌浪传播过程模拟

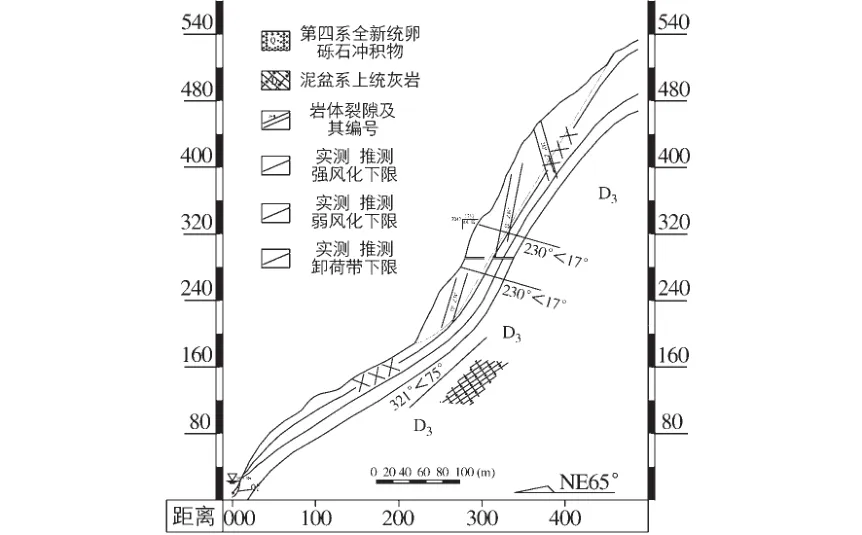
图1 变形体A区计算剖面(单位：m）Fig.1 Calculating profile of deformation zone A (unit：m）

2.1 滑体滑速计算

变形体总量约372万m3，位于库区右岸河道拐弯处，其下游河道相对较平直，距下坝址约1.7 km。因变形体规模较大、分布高程高，现状条件下变形迹象明显，在未来电站的运行条件下其一旦失稳将对下游建筑物的运行存在严重的威胁，故在本设计阶段针对近坝库岸变形体进行稳定性分析和评价，对可能失稳后涌浪高度进行预测，以研究涌浪对库区沿岸建筑物的影响。

涌浪计算的前提是滑速计算，目前对于滑坡失稳后滑速计算方法很多，其中应用较多的主要有潘家铮法。该方法把滑坡体剖分为若干条块，更接近实际滑坡体结构，同样具有可操作性强等特点。因此，本文采用潘家铮法计算变形体可能失稳后的最大滑速，具体计算方法可参考文献［6］。以该变形体A区为例(见图1），将整个滑体划分12个条块，条块宽度为ΔL=20 m，滑带抗剪参数tanφ=0.499，c=259 kPa；滑坡开始滑动ΔL为1步，共计算12步，其中在第7步时，滑体滑速达到最大，其值为υ=24.29 m/s。

2.2 涌浪模拟模型

该变形体为近坝库岸边坡，为了分析涌浪传播至对岸和涌浪沿河道传播的规律，分别建立对岸涌浪计算模型和沿河岸涌浪二维计算模型(图2），数值模型的几何模型和网格划分利用FLUENT软件的前置处理器GAMBIT完成。考虑动网格模型的操作性，数值模拟简化如下：①滑体简化为矩形刚性滑体，岸坡简化为梯形谷；②为了考虑滑体受水的阻力和地形的影响，假定滑体以一定的速度入水后，即开始减速；③模拟计算时，水位为正常蓄水位，此时水深为250 m，假定坝顶高程比正常水位高5 m，即大坝高255 m，上游坡比为1：1.4，坝顶宽度12 m，不考虑坝顶防浪墙作用。

初始涌浪计算模型见图2(a），库区右岸均简化为59°斜坡，模型总高551 m，库底宽度为64 m，水深250 m，滑体简化为矩形刚体，厚度为25 m，落水点距对岸的水面宽度约为280 m。计算模型共计51 593个节点，152 279个单元。模拟计算时间步Δt=0.5 s，计算总时间为54 s。

沿河岸模拟计算简化为二维平面模型，其局部模型(推荐坝址处，距落水点2 130 m）见图2(b），水深250 m，大坝高255 m。计算模型共计89 735个节点，193 717个单元。模拟计算时间步Δt=0.5 s，计算总时间为195 s。

图2 河道涌浪形成过程计算模型Fig.2 Numerical model for surge formation process

2.3 涌浪模型初始化参数

上述2个模型的计算参数一致：模型计算采用二维非定常分离隐式求解算法；采用VOF两相流，初相和第二相分别设置为空气和水，自由面重构为Geo.Reconstruct格式。湍流模型采用RNG κ-ε模型，近壁区采用标准壁面函数法，除模型顶部为压力进口边界，其他均为壁面边界，2个模型初始化后见图3。

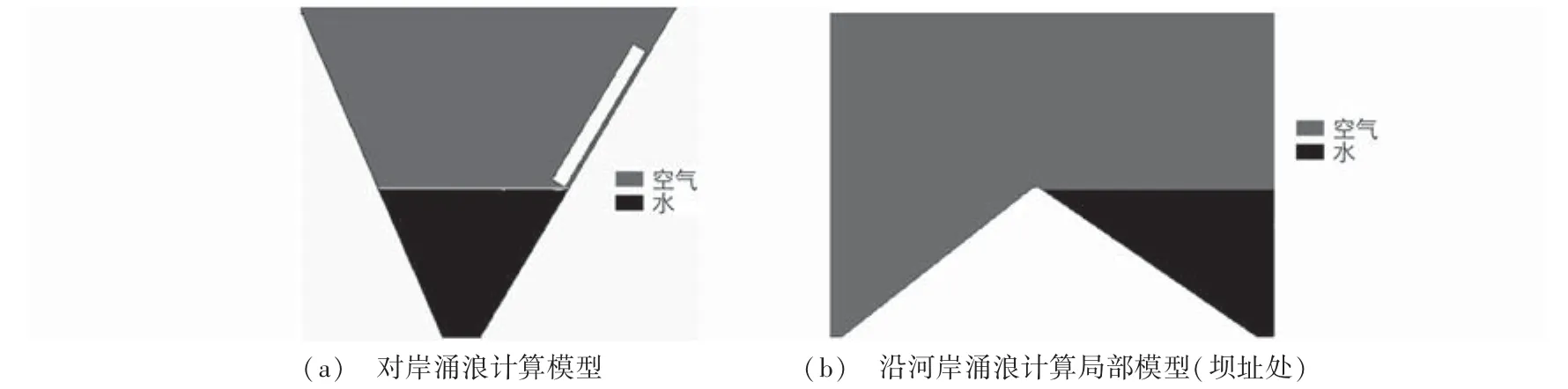
图3 涌浪数值模型初始化Fig.3 Initialization for surge numerical model

计算考虑重力影响，设空气密度为周围环境的流体密度。本文采用刚性滑块的模拟滑动入水，其运动边界类型属于刚性运动边界，因此在动网格模型中选用了基于弹性变形的网格更新法和局部网格重构法。滑体入水速度为24.29 m/s，并采用UDF编写速度程序实现。

3 涌浪形成过程及形态分析

3.1 初始涌浪形成过程

滑体入水后，初始涌浪高度变化过程线见图4。(右岸）水面随时间的变化形态见图5。由图可知，滑体入水时高速挤压和冲击水面，水面开始翻卷，并溅起巨大浪花，形成初始涌浪；在t=4 s时，初始涌浪高度达最大值(22.04 m）；而后涌起浪花开始下降，伴随波浪飞溅及其破碎，水体相互作用形成第1次波峰向对岸推进。

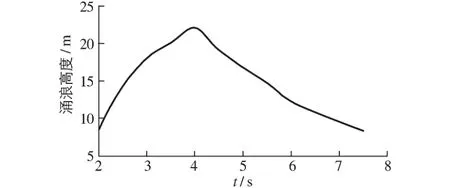
图4 落水点初始涌浪高度变化Fig.4 Changes in surge height with time

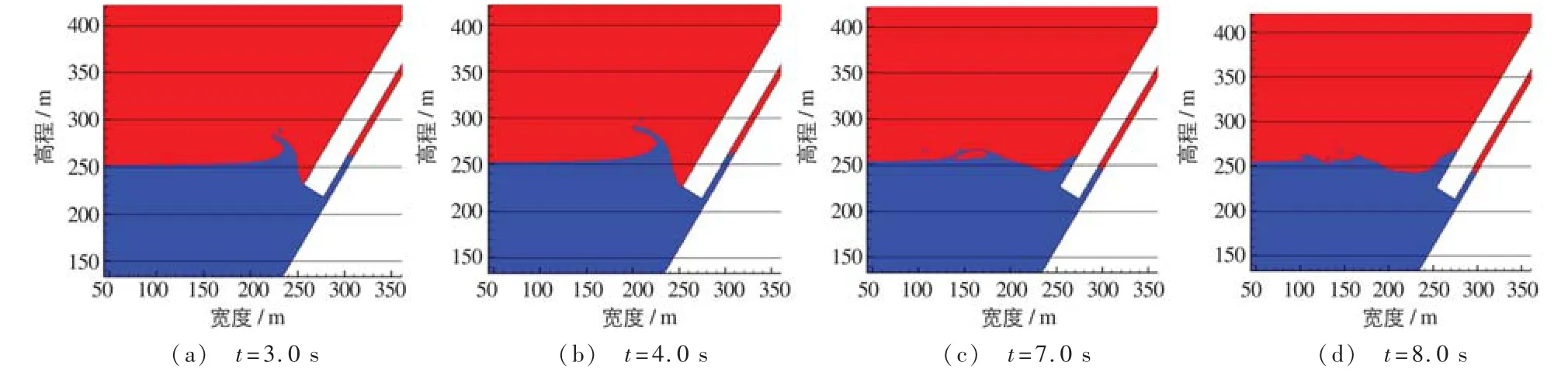
图5 入水点涌浪形态随时间的变化Fig.5 Changes in surge patterns with time

3.2 对岸涌浪形态分析

滑体入水后，涌浪高度变化过程见图6。对岸(左岸）水域水面随时间的变化见图7。其由图6和7可知：涌浪传播至对岸后经历了沿岸爬坡、跌落、叠加、衰减的过程，可分为以下3个阶段：

(1）初始涌浪爬升阶段。当t=11.5 s，初始涌浪传播至左岸附近水域，由于涌浪的持续推进，该区域的水体受到了岸壁(左岸）和涌浪的双重挤压作用，水面升高较快。当t= 12.5～13.0 s时，初始涌浪到达岸边，在左岸迅速爬升，涌浪最大爬坡高度为13.58 m。

(2）涌浪跌落和次浪碰撞叠加阶段。涌浪爬升至最高点后快速跌落最低点，其水面的变化形态见图7所示。此时(t=21.0 s），由于右岸涌浪次波峰传播此水域，水面的落差较大，在巨大落差的作用下水体又开始朝左岸推进，并再次在左岸坡迅速爬升，形成更高的涌浪，在t=26.0 s时达到最大，涌浪爬坡最大高为18.58 m。

(3）涌浪衰减阶段。涌浪爬坡达到最高点后，左岸涌浪高度不断衰减，其中，在t=37.0 s时，高度为14.25 m，在t=49.0 s时，高度为8.22 m。

上述分析表明，初始涌浪在左岸引起的涌浪高度为13.58 m，但随着初始涌浪的跌落和次波的碰撞叠加作用，水库水面发生反复震荡现象，其最大涌浪高度达到18.58 m。

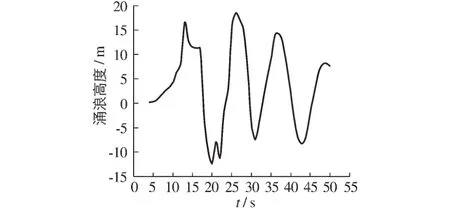
图6 对岸涌浪高度变化过程线Fig.6 Height-change hydrograph of surge with time of the other bank side

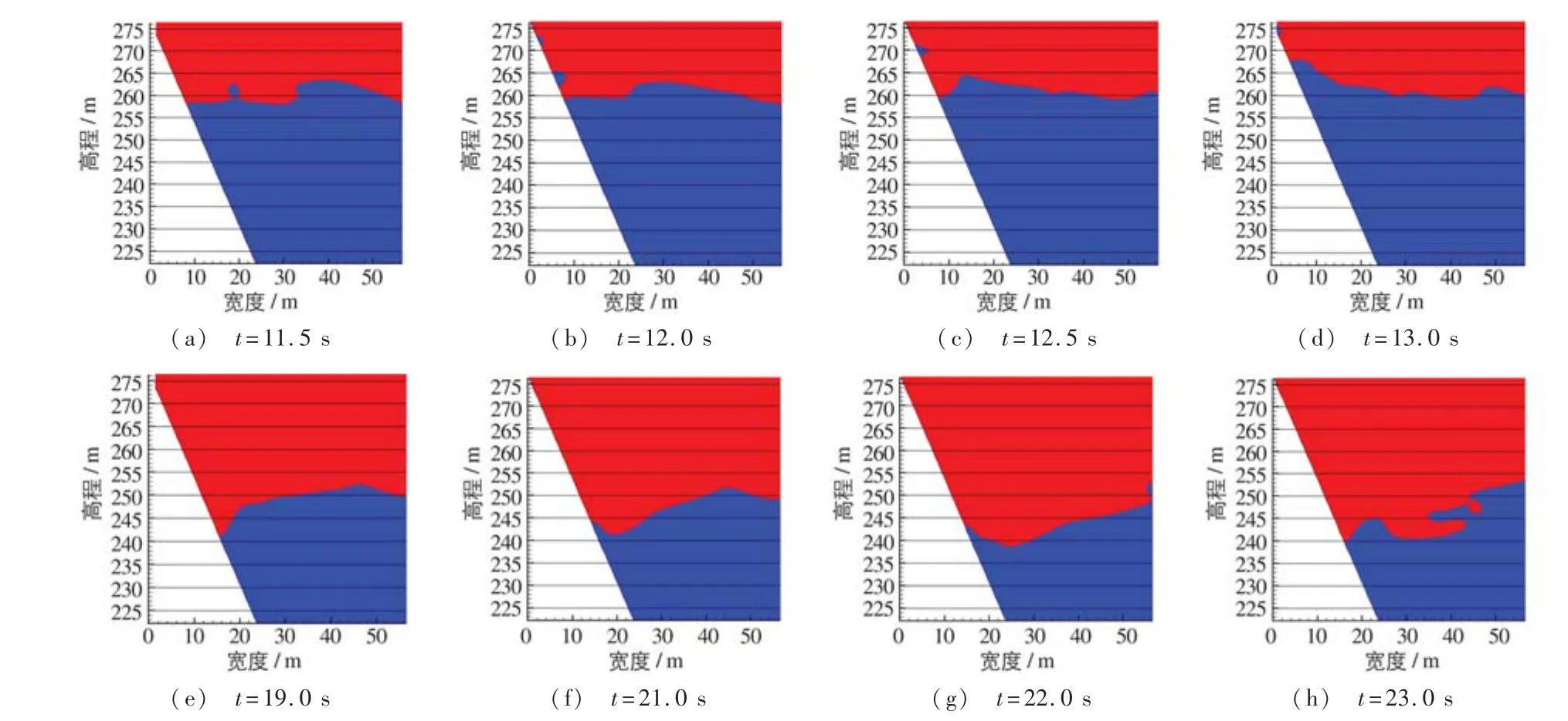
图7 对岸涌浪形态随时间变化Fig.7 Changes in surge patterns with time along the other bank side

3.3 涌浪沿岸传播过程分析

为了分析涌浪向下游传播过程，分别选取在距滑体落水点约280 m(相当于对岸距离），600 m，1 200 m位置(依次命名测点A，B，C），记录其涌浪高度与时间的关系(见图8）。

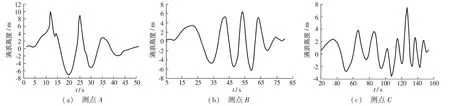
图8 测点A，B，C涌浪高度变化Fig.8 Changes in surge height with time at points A，B and C

由图8可知：初始涌浪第1次波峰通过测点A，B，C位置的时间分别是12.0，21.0和35.0 s，相应涌浪高度分别为9.88，3.44和2.42 m，表明随着初始涌浪持续推进，其能量不断衰减。这与其他学者研究的规律较为一致［10-11］。

初始涌浪通过测点A，B，C后，各测点位置水面高度的变化规律却各不相同：测点A的涌浪高度不断减少，在约50 s后水面趋于平静；测点B的涌浪高度不断增加，当t=43.0 s，涌浪高度达到最大，为5.22 m，而后不断减小，在约75 s后趋于平静；测点C的涌浪高度达到最大时经历的时间较长(t=127.0 s），其过程也较为复杂。上述表明，近坝测点B和C点涌浪高度均受到库区水体相互挤压叠加影响，最终形成更高的涌浪，其中C点位置的涌浪高度变化更容易受到大坝建筑物的影响。

4 涌浪高度计算的讨论和分析

4.1 坝址处涌浪高度分析

滑体入水后，涌浪高度变化过程见图9，坝前位置(测点D）的水面随时间变化形态见图10。由图9和10可知：在t=58.5 s时，坝前初始涌浪最高点达到坝顶高程，在t=60 s时，涌浪达到最高，为6.11m，超过坝顶1.11m。但由于此时坝前水体运动缓慢，且坝前水域的水体开始回落，水体呈倒V型，坝顶上水体未能继续推进，并没有翻过大坝。

在坝址处，由于大坝对水体的阻挡作用，数值模拟计算涌浪高度达6.11m，虽水体最终未能过坝，为了避免涌浪对大坝正常运行产生不利的影响，建议坝顶防浪墙顶高程应超过正常水位至少7 m。

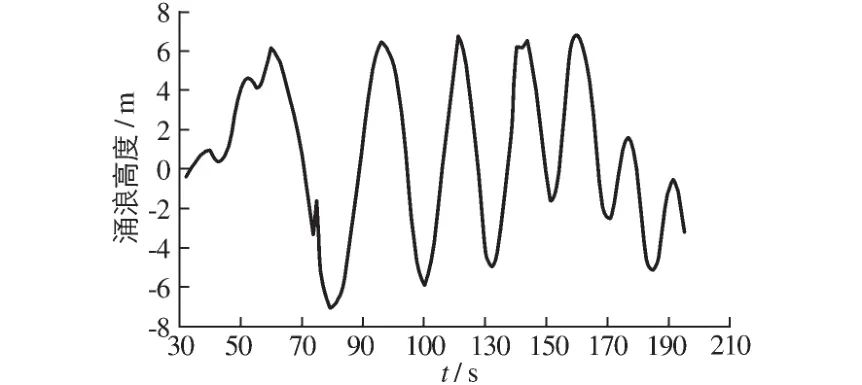
图9 坝址位置涌浪高度变化Fig.9 Changes in surge height with time at dam site

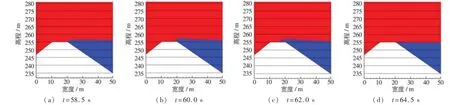
图10 坝址处涌浪形态随时间变化Fig.10 Changes in surge patterns with time at dam site

4.2 与潘家铮法计算结果比较

本节采用潘家铮法计算该变形体可能失稳后的涌浪高度，其计算参数如下：河谷宽B=280 m，滑坡平均宽度L=248 m，库水深度(平均水深）h=172 m，A区滑坡体离下坝址距离X0=2 130 m；滑体平均厚度λ= 25 m，系数m=1.17，滑坡速度υ=24.29 m/s。最终计算在落水点产生初始波高ζ0=17.30 m，对岸产生的涌浪高度ζmax=8.99 m，并分别计算下游沿岸280，600，1 200和2 130 m位置的涌浪高度，见表1所示。

由表1可知，在落水点及对岸处，模拟计算的初始涌浪高度比潘家铮法计算结果大；这是由于数值模拟能反映初始涌浪形成以及涌浪在岸坡上爬高过程，其过程均伴随着巨大水花，并采用水花的最高点计算为涌浪高度，计算结果比潘家铮法计算结果稍大。而离落水点在较远的水域(测点B、测点C）浪高与潘家铮法计算结果相差不大，且初始涌浪沿岸传播衰减过程一致，表明数值模拟能较好反映涌浪沿岸传播过程。

表1 涌浪高度计算分析Tab.1 Analysis of surge height calculation m

考虑挡水建筑物对库区涌浪高度的影响后，库内涌浪推进和库内水体相互作用下，库区测点B、C以及坝址处的最大涌浪高度均远大于初始涌浪高度，并大于潘家铮法计算结果。这是由于潘家铮法是基于库水单向流分析水库涌浪问题，无法反映由大坝挡水引起库区水面反复震荡，水体之间的复杂作用过程。数值模拟能较好地反映由大坝挡水引起库区水体之间复杂作用和涌浪叠加过程，最终计算出库区内沿岸及坝址处的最大涌浪高度也更符合实际。

5 结 语

本文基于流体计算软件FLUENT，以某水电站库区近坝变形体为例，模拟其可能失稳后引起的水库涌浪问题，得出以下结论：

(1）初始涌浪形成时，滑体入水高速挤压水体，落水处水面翻转，涌浪形成过程中伴随着巨大水花；涌浪传播至对岸后，在岸坡上有较大的爬高(13.58 m），而后库区水面反复震荡，岸坡浪高达最大值(18.58 m）后开始衰减。

(2）随着初始涌浪的推进，对沿岸各点的初始涌浪高度影响不断减小。但由于库区水体运动受大坝建筑物的阻挡，并形成向上游推进的波浪，两个方向的水体相互挤压叠加作用，库区水面反复震荡，造成库区部分水域形成更高的涌浪。因此，从灾害防治角度看，由叠加作用形成的涌浪可能会对沿岸的居民和建筑物造成更大的危害。

(3）在坝址处，水体受到大坝阻挡作用，计算涌浪爬高达6.11 m，虽涌浪最终未能过坝，为了避免涌浪对大坝正常运行产生不利的影响，建议坝顶防浪墙顶高程应超过正常水位至少7 m。

(4）通过数值模拟实现了滑体入水全过程，可真实反映波浪在岸坡上爬坡，以及库区水面反复震荡和叠加作用；能较好地模拟由大坝挡水引起库区水体之间复杂作用过程，考虑了大坝对水体阻挡作用，计算出库区内沿岸及坝址处的最大涌浪高度更符合实际情况，为库区涌浪灾害防治和工程设计提供科学依据。

［1］VISCHER D L，HAGER W H.Dam hydraulics［M］.Chichester：Wiley，1998.

［2］汪定扬，刘世凯.长江新滩滑坡(1985年6月）涌浪调查研究［J］.人民长江，1986，17(10）：24-27.(WANG Ding-yang，LIU Shi-kai.Investigation of the surge effect caused by the landslide at Xintan，Yangtze River［J］.Yangtze River，1986，17 (10）：24-27.(in Chinese））

［3］潘家铮.建筑物的抗滑稳定和滑坡分析［M］.北京：水利出版社，1980.(PAN Jia-zheng.Stability of construction against sliding and landslide analysis［M］.Beijing：Water Conservancy Press，1980.(in Chinese））

［4］陈学德.水库滑坡涌浪的经验算法及程序设计［R］.武汉：水利电力部中南勘测设计院科研所，1984：1-18.(CHEN Xue-de.Experiential method and program design of surge triggered by landslide in reservoir［R］.Wuhan：Science and Research School in Zhongnan Institute of Reconnaissance and Design of the Ministry of Water Conservancy and Electric Power，1984：1-18.(in Chinese））

［5］袁银忠，陈青生.滑坡涌浪的数值计算及试验研究［J］.河海大学学报，1990，18(5）：46-53.(YUAN Yin-zhong，CHEN Qing-sheng.Experimental study of landslide-induced surge in reservoirs and numerical calculation［J］.Journal of Hohai University，1990，18(5）：46-53.(in Chinese））

［6］殷坤龙，刘艺梁，汪洋，等.三峡水库库岸滑坡涌浪物理模型试验［J］.地球科学：中国地质大学学报，2012，37(5）：98-104.(YIN Kun-long，LIU Yi-liang，WANG Yang，et al.Physical model experiments of landslide-induced surge in Three Gorges Reservoir［J］.Earth Science(Journal of China University of Geosciences），2012，37(5）：98-104.(in Chinese））

［7］王晓鸿，刘汉超，张倬元.滑坡涌浪的二维有限元分析［J］.地质灾害与环境保护，1996，7(4）：19-22.(WANG Xiaohong，LIU Han-chao，ZHANG Zhuo-yuan.A two dimensional FEM analysis of surge induced by landslide［J］.Journal of Geological Hazards and Environment Preservation，1996，7(4）：19-22.(in Chinese））

［8］杜小弢，吴卫，龚凯，等.二维滑坡涌浪的SPH方法数值模拟［J］.水动力学研究与进展：A辑，2006，21(5）：581-586. (DU Xiao-tao，WU Wei，GONG Kai，et al.Two dimensional SPH simulation of water waves generated by underwater landslide［J］.Journal of Hydrodynamics(SerA），2006，21(5）：579-586.(in Chinese））

［9］宋新远，邢爱国，陈龙珠.基于FLUENT的二维滑坡涌浪数值模拟［J］.水文地质工地质，2009(3）：90-94.(SONG Xinyuan，XING Ai-guo，CHEN Long-zhu.Numerical simulation of two-dimensional water waves due to landslide based on FLUENT［J］.Journal of Hydrology and Engineering Geology，2009(3）：90-94.(in Chinese））

［10］刘世凯.长江西陵峡新滩滑坡涌浪高度衰减因素初探［J］.水利水电技术，1987(9）：11-14.(LIU Shi-kai.A first study on factors attenuating height of surge caused by Xintan landslide in Xiling Gorge，Yangtze River［J］.Water Resources and Hydropower Engineering，1987(9）：11-14.(in Chinese））

［11］汪洋，殷坤龙.水库库岸滑坡涌浪的传播与爬高研究［J］.岩土力学，2008，29(4）：1031-1034.(WANG Yang，YIN Kun-long.Research on propagation and surge runup triggered by landslide in reservoir［J］.Rock and Soil Mechanics，2008，29 (4）：1031-1034.(in Chinese））

Numerical simulation of the surge based on FLUENT software

DENG Cheng-jin，YUAN Qiu-shuang，HOU Yan-hua，JIA Wei
(HydroChina Xibei Engineering Corporation，Xi′an 710065，China）

Based on the fluid calculation FLUENT software，surge changes within the reservoir area and its propagation along the reservoir bank，caused by possible instability of the landslide-induced deformation body in the reservoir area of a hydropower station，have been simulated.Some impacts of the water retaining structure upon surge propagation along the reservoir bank are taken into consideration and analyzed，and the initial swell height，and the maximum wave height along the opposite bank，the reservoir bank and the dam site are obtained by calculation analysis，and compared with the calculated results given by PAN Jia-zheng method.Analysis results show that the numerical simulation can well reflect the wave run-up process over the bank slope and wave propagation along the reservoir banks，and the interaction by the wavy water surface and the surge superposition in the reservoir area is actually simulated.Due to barrier effect given by the dam structure，a higher swell is formed by repeated water surface oscillation with the surge superposition in the reservoir area.Thus the calculated initial swell and the maximum surge height within the reservoir area well conform to the actual situation，which can provide references for the engineering design and surge disaster prevention of the reservoir area close to the dam site.

reservoir area；landslide；waves run-up process；the maximum surge；surge superposition；water retaining structure；numerical simulation

TV697；O242 文献标心码：A

1009-640X(2014）03-0084-08

2013-10-29

邓成进(1986-），男，湖北随州人，助理工程师，硕士研究生，主要从事水工设计及边坡数值模拟研究。E-mail：dengchengjin@nwh.cn