基于Kalman算法的软测量技术在电池容量检测中的应用

王凤国， 张忠相， 欧阳松， 武青芬

（北京航天发射技术研究所，北京 100076）

基于Kalman算法的软测量技术在电池容量检测中的应用

王凤国， 张忠相， 欧阳松， 武青芬

（北京航天发射技术研究所，北京 100076）

针对如何在线准确检测实际工作中发射车车载电池容量，提出了一种基于Kalman算法的软测量方法。首先，建立蓄电池数学模型，选择可测、易测的辅助变量，利用Kalman算法建立软测量模型；然后，使用试验数据，通过参数辨识求解软测量模型；最后，利用Matlab软件对该模型进行仿真以及现场试验。结果表明：采用Kalman算法的软测量技术减少了电池应用过程中的电流累积误差，提高了电池容量的检测精度。

计量学；电池容量；Kalman算法；软测量；数学模型

1 引 言

随着信息化、智能化程度的提高，蓄电池以具有发热小、无噪声、无污染、易伪装等优点，在某些发射车中得到广泛应用。为了判断蓄电池在工作过程中电量是否充足，状态是否良好；并避免电池在使用过程中出现过充或过放的情况，以进一步发挥电池的性能，延长使用寿命，可靠地完成各项任务，有必要对电池的可用容量进行准确地检测。

常用的电池容量检测方法有开路电压法、电流积分法和电阻法［1］。开路电压法只能在一定条件下用于静态电池容量的检测，不能用于动态容量的检测，因此一般只用于上电预估；电流积分法没有考虑电池初始状态，且电流采样和充放电效率误差引起的累积误差逐渐增大［2］，会导致检测误差增大，该方法不能单独用于电池容量检测；电池内阻包括欧姆内阻和极化内阻，极化内阻难于测量，且电池电阻与容量的对应关系规律性不强，对硬件和软件要求较高，因此此方法较少用于工程中。Kalman算法是将电池看成一个系统，电池容量是系统中一个内部状态，与其它方法相比，非常适合于电流波动较大，充、放电切换频繁的情况［3］。

由于电池容量无法或难以用传感器直接检测，因此本文采用基于Kalman算法的软测量技术，充分利用检测过程中易于获取的辅助变量（测量参数），按照辅助变量与主导变量（被测参数变量）之间的数学关系，建立软测量模型；通过模型辨识、最优估计及推断来确定主导变量［4，5］。其实质是要完成由辅助变量构成的可测信息x到主导信息估计y的映射，即y＝f（x）。但软测量模型不同于一般意义的数学模型，它强调的是通过辅助变量x获得对主导变量y的最优估计。此方法简单易行，且便于在线实时测量操作，测量精度相对较高，具有较好的实用价值。

2 基于Kalman算法的软测量模型

2.1 Kalman滤波算法

卡尔曼滤波算法是匈牙利数学家Kalman于1960年提出，是一种线性最优递推方法，研究的是当系统的状态方程和量测方程中具有随机噪声时，对系统状态变量的最小方差估计。由于卡尔曼滤波算法是递推算式，所以它不仅适用于实时预测和滤波，而且适于在嵌入式系统上实现［6］。

假定线性随机系统的状态方程和量测方程分别为

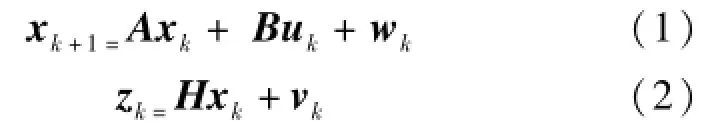
式中，xk＋1为k＋1时刻状态向量；zk为k时刻观测向量；uk为k时刻输入向量；A为系统矩阵；B为控制输入矩阵；H为量测矩阵；wk为过程激励噪声，其包含输入扰动和系统模型偏差；vk为量测随机噪声。

当式（1）中wk和式（2）中vk相互独立时，其正态分布的白色噪声为

式中，Q为过程激励噪声协方差矩阵；R为量测随机噪声协方差矩阵。

为了用于嵌入式系统控制，根据时变线性连续系统，对式（1）和式（2）进行变换，得到卡尔曼滤波算法的递推方程，即时间更新方程（预估方程）和量测更新方程（校正方程），见表1［7，8］。

表1 Kalman算法递推方程

其中，时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计。量测更新方程负责反馈，将先验估计和新的量测变量结合，以构造改进的后验估计。最后，时间更新方程和量测更新方程构成具有数值解的预估——校正算法，见图1。

图1 离散Kalman算法循环更新图

2.2 软测量模型

2.2.1 建立蓄电池数学模型

本文以铅酸蓄电池为研究对象，首先对铅酸电池建立数学模型，根据此数学模型，列出容量与电流、电压、温度、内阻之间的关系。所建立的模型必须能较好地体现电池的动态特性，且阶数不能太高，以减少处理器运算，易于工程实现。鉴于以上考虑，选用Thevenin电池模型，如图2所示。

2.2.2 构建电池数学方程

为了描述电池剩余可用容量，一般用电池荷电状态（State of Charge，SOC）描述，此处用x表示，其定义为x＝Qr／Qe，其中，Qr为电池剩余容量；Qe为电池有效容量。根据电池荷电状态的定义、安时积分法及k时刻的SOC，递推k＋1时刻的SOC，即状态方程为

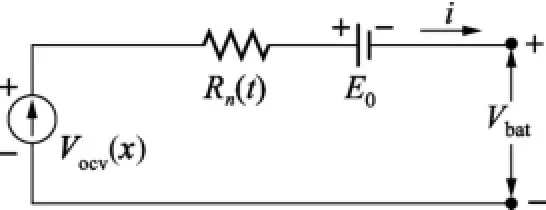
图2 Thevenin电池模型

式中，x（k＋1）为k＋1时刻电池的荷电状态；x（k）为k时刻电池的荷电状态；ik为充放电电流，规定充电为正，放电为负；ηi为i时电流的充放电效率，与电流、温度和循环寿命有关，在室温及标称电流状态下，通常取1，在其他状态下，需要根据电池试验数据查表插值求得；Δt为采样周期；Qe为电池的有效电量，即为电池能放出的容量，由Peukert方程得到。

利用Thevenin电池模型，得到量测方程

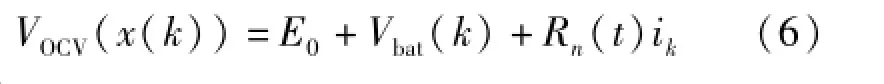
式中，VOCV（x（k））为蓄电池开路电压，电池k时刻电池荷电状态的函数；Vbat（k）为k时刻电池的端电压；E0为电池极化电动势；Rn（t）为电池内阻；ik为电池充放电电流。其中，Rn（t）与循环寿命（电池新旧程度）有关，需要根据电池试验数据查表插值求得。

根据电池的开路电压与电池荷电状态的非线性关系，将蓄电池的开路电压拟合成电池荷电状态的4次多项式

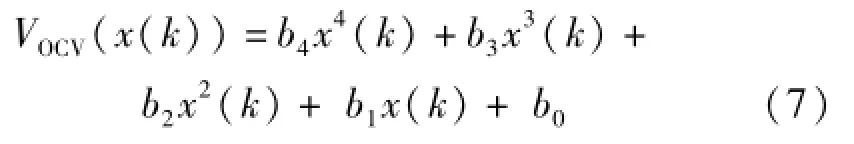
式中，多项式系数b0～b4通过对电池充放电试验数据进行拟合得到。

联立式（5）、式（6），得到优化的电池软测量模型为

式中，VOCV（x（k））＝b4x4（k）＋b3x3（k）＋b2x2（k）＋b1x（k）＋b0；ηi＝f（i，t，T），通过查表插值得到；Δt为采样周期；E0＝g（i，t，T）为电池极化电动势，通过查表得到；Rn（t）为蓄电池内阻，与循环寿命（电池新旧程度）有关，在程序中通过查表插值得到。

由Peukert方程，可得

其中，n为Peukert方程系数，由试验数据求得；Is为标准充放电电流，本文取27A；Ia为采集到的实时电流；Qs为540Ah，即标称容量。

将电池软测量模型代入Kalman算法递推方程，得到电池荷电状态SOC递推的结构图如图3所示。

图3 电池荷电状态递推结构图

3 仿真结果与试验分析

依据建立的电池软测量模型及图3电池荷电状态递推结构图，利用Matlab建立电池仿真模型，将试验数据带入仿真模型得到仿真结果，见图4。

由图可以看出，通过模型估算的电池端电压和SOC均向真值自动收敛，且误差较小。说明：（1）所建立的电池容量检测软测量模型反映端电压、电流、温度与电池容量的内在关系；（2）采用的卡尔曼滤波算法满足检测精度要求。

为进一步验证该模型的正确性以及容量检测的精度，分别对6块（2串3并）铅酸蓄电池68025D在常温下进行240 A、120 A、90 A、30 A放电试验，其中240 A及30 A的实测与检测值（估算值）对比试验数据见图5。

由图5可以看出：（1）电池放电初期端电压随容量的减少缓慢下降，后期到达放电拐点后随容量的减少急剧下降；（2）放电电流较大时，放电曲线误差较大，主要与算法中应用的Peukert方程指数系数设置有关，分段设置该指数系数，可以提高容量检测精度；（3）放电初期容量检测误差较大，主要由于初始上电预估给定值引起，随着Kalman算法的收敛，误差越来越小，所以该方法更适合用于充放电循环的场合。

4 结 论

本文在应用Thevenin电池模型的基础上，利用Kalman算法建立了电池容量检测软测量模型，并用Matlab对该模型进行仿真，仿真结果表明该模型适于电池容量检测；用不同放电电流验证，电池电量估算精度较高，满足型号任务应用需求。从而，通过测量易测的辅助变量电池端电压、电流和温度，得到主导变量电池容量／SOC，为电池容量的间接在线准确测量提供了一种新的有效的实时测量方法。

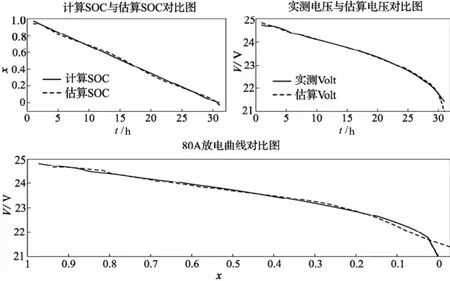
图4 24 V／540Ah电池单循环仿真图

图5 蓄电池放电曲线对比图

［1］ 冯楠，王振臣，胖莹.基于自适应遗传算法和BP神经网络的电池容量预测［J］.计量学报，2012，33（6）：546－549.

［2］ 吴红杰，齐铂金，郑敏信，等.基于Kalman滤波的镍氢动力电池SOC估算方法［J］.北京航空航天大学学报，2007，33（8）：945－948.

［3］ 林成涛，王军平，陈全世.电动汽车SOC估计方法原理与应用［J］.电池，2004，34（5）：376－378.

［4］ 王超厚，罗良玲，徐晗.软测量技术及其在刀具故障诊断中的应用［J］.工具技术，2007，41（10）：69－71.

［5］ 黄凤良.软测量思想与软测量技术［J］.计量学报，2004，25（3）：284－288.

［6］ 夏超英，张术，孙宏涛.基于推广卡尔曼滤波算法的SOC估算策略［J］.电源技术，2007，131（5）：414－417.

［7］ Welch G，Bishop G.An introduction to the Kalman filter.University of North Carolina［EB］.http：／／www. cs.unc.edu／～welch／media／pd f／kalman_intro.pdf，2012-06-14.

［8］ Kalman R E.A New Approach to Linear Filtering and Prediction Problems［J］.TransactionsoftheASMEJournalofBasicEngineering，1960，82（1）：35－45.

App lication Soft-sensing Technique Based on Kalm an Algorithm for Battery Capacity Detection

WANG Feng-guo， ZHANG Zhong-xiang， OUYANG Song， WU Qing-fen
（Beijing Institute of Space Launch Technology，Beijing 100076，China）

In order to accurately detect the practical work capacity of battery for the emission car，a kind of Kalman algorithm based on soft-sensingmethod is put forward.First of all，the batterymathematicalmodel is established，then，the soft-sensingmodel is built with selecting measurable，easy measurement auxiliary variables and Kalman algorithm；and then，the soft-sensingmodel is attained with historical test data and the parameter identificationmethod.Finally，themodel is simulated by the Matlab software and tested field.The results show that soft-sensing technique with Kalman algorithm reduces the current cumulative error of battery in the process of application，and improves the battery capacity detection accuracy.

Metrology；Battery capacity；Kalman algorithm；Soft-sensing；Mathematicalmodel

TB971

A

1000-1158（2014）02-0165-04

10．3969／j．issn．1000-1158．2014．02．15

2012-06-14；

2013-12-04

王凤国（1981－），男，山东临沂人，北京航天发射技术研究所工程师，硕士，主要研究方向为供配电、电力电子测量技术。wfg5641＠163.com