基于椭圆假设的单对磁编码器误差补偿方法

曾一凡， 姜芳芳

（沈阳工业大学信息科学与工程学院，辽宁沈阳 110870）

基于椭圆假设的单对磁编码器误差补偿方法

曾一凡， 姜芳芳

（沈阳工业大学信息科学与工程学院，辽宁沈阳 110870）

研究了一种单对磁极磁编码器的误差补偿方法。针对单对磁极磁编码器中存在的零位误差、灵敏度误差、正交误差和铁磁干扰等每一种误差进行分析，得出各自的误差表达式。为了便于误差补偿，总结出描述这种误差共性的表达式，此式将误差的形成过程假设为圆到椭圆的变化过程，其逆过程就是误差补偿的过程。实验结果表明，利用此种方法的磁编码器精度达到了0.02°，误差补偿效果明显。根据此方法研究的磁编码器具有成本低、精度高、使用方便的特点。

计量学；磁编码器；误差补偿；椭圆假设；单对磁极

1 引 言

磁编码器是一种可将角位移、角速度、旋转角位置等物理量转换为电信号的传感器。相对于光电编码器，它的结构简单、抗振动、成本低、功耗小、响应速度快，而且不易受粉尘、水汽的影响。在运动控制系统中已经成为必不可少的组成部分，其市场需求量每年以20%～30%的速度增长［1～3］。

由于制造和环境因素的影响，磁编码器角度测量系统出现的零位误差、灵敏度误差、正交误差、铁磁干扰等会影响磁编码器的精度和分辨率。针对磁编码器角度测量系统的误差，文献［4］提出了数字标定法来精确分析测角系统的误差，采用去除奇异值滤波或限幅滤波等简单的数字滤波方法将毛刺信号滤掉，采用误差曲线拟合法补偿正交误差。该方法能提高测角系统的精度，但是算法复杂，对误差来源分析不够全面。文献［5］中提出霍尔元件的安装位置和体积都会影响磁传感器的测量精度。文献［6］也提出传感器自身会存在误差，霍尔元件本身存在零位误差、温度误差和灵敏度误差，在设计中可采用电桥电路进行零位误差补偿，对温度和灵敏度误差可采用恒流源和软件方法进行补偿。该方法可以估算出传感器的总体均方误差，但其中采用了硬件电路进行误差补偿，电路的稳定性会影响补偿的精度。文献［7，8］提出先进的自适应数字相位锁相环（AADPLL），主要针对相位误差进行补偿，但是并没有完全解决输入信号的带宽问题，以及正交输入相位的错误。采用正弦信号的自动校正法补偿直流偏量、相位和幅值偏差，虽然有一定的理论价值，但是算法比较复杂。

目前，针对单对磁编码器，并没有相关文献提出几种不同的误差源共同作用时的误差补偿方法。本文提出的方法能全面考虑磁编码器的各种误差来源，并对每一种误差源进行分析和补偿，而且实现简单、运算量小，能有效提高角度测量的精度。

2 磁编码器误差理论分析

单对磁极磁编码器是在磁体下方某一平面内处于正交位置处放两个霍尔元件，其结构如图1所示。

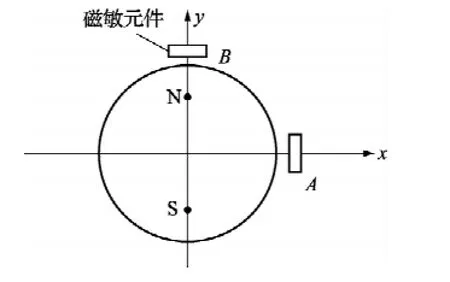
图1 单对磁极磁编码器结构

理论上，在没有误差的情况下，磁编码器输出的两路信号Hx，Hy合成向量的顶点在平面上从0°到360°变化一周的轨迹是圆［9，10］。但是在实际情况中，由于制造和环境等因素的影响，必然会存在误差。只要磁编码器有误差就会反映在Hx和Hy的变化上，从数学上描述Hx和Hy合成向量顶点的轨迹将变为一个椭圆。将椭圆变回圆的过程即为误差补偿的过程。磁编码器的误差主要分为零位误差、灵敏度误差、正交误差、铁磁干扰等。

为了便于误差补偿，分析每一种误差之间的共性，总结出误差共性分析的表达式：

式中，a11、a12、a21、a22、b1、b2称为误差系数。其中，a11、a12、a21、a22是软磁材料、霍尔元件安装不垂直、灵敏度以及电路的放大倍数不同等因素引起的；b1和b2是由硬磁材料和电路零位引起的。

3 磁编码器误差补偿分析

为了便于误差信号的补偿，分析各种误差之间的共性，总结出表达式（1）。

根据式（1）可以由Hx2，Hy2求出没有误差的Hx和Hy，其表达式为：

式中，Ce和De称为误差补偿系数，可由误差系数求得。

4 椭圆假设

单对磁极磁编码器的误差补偿采用的是基于椭圆假设的误差补偿，即误差的形成过程看作是圆到椭圆的变化过程，把式（1）改写成

式中，Kx，Ky是与灵敏度有关的系数，φp是与制造及软磁材料影响有关的系数，φs是与安装有关的系数。正交矩阵φs将圆转了一个角度φs；对称矩阵φp使圆变成椭圆；对角矩阵K将椭圆转了一个角度；B的作用是改变了椭圆的中心位置。

从几何角度看，误差形成过程是一个由圆到椭圆的变化过程，所以把这个假设称为椭圆假设。

根据椭圆的一般方程

式中，是与地磁场强度有关的常数，可由采样数据确定。只要有足够的试验数据Hx2和Hy2，就可以确定椭圆方程的系数c1，c2，c3，c4，c5，从而确定该椭圆。根据椭圆假设，只要能求出φp、Kx、Ky、b1和b2，就可以求出误差系数和误差补偿系数，完成误差补偿。

求解误差系数时，只需使用5个角度上采集的数据，设采样数据为Hx2i和Hy2i（i＝1，2，3，4，5），但试验数据的随机误差将影响补偿效果。采用最小二乘法能有效的减小随机误差。

由式（4）可得如下方程组：

根据最小二乘原理得到系数矩阵：

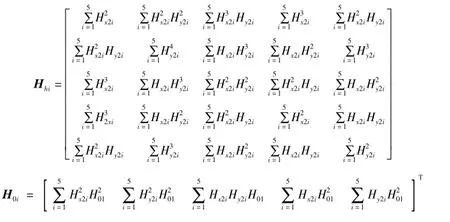
通过最小二乘法求出椭圆系数c1，c2，c3，c4，c5，它们与各误差系数之间的关系：

式中，Δ是由采样数据决定的常数。通过以上各式可以求出误差补偿系数Ce，De。

5 实验设计与结果分析

（1）实验系统结构如框图2所示：

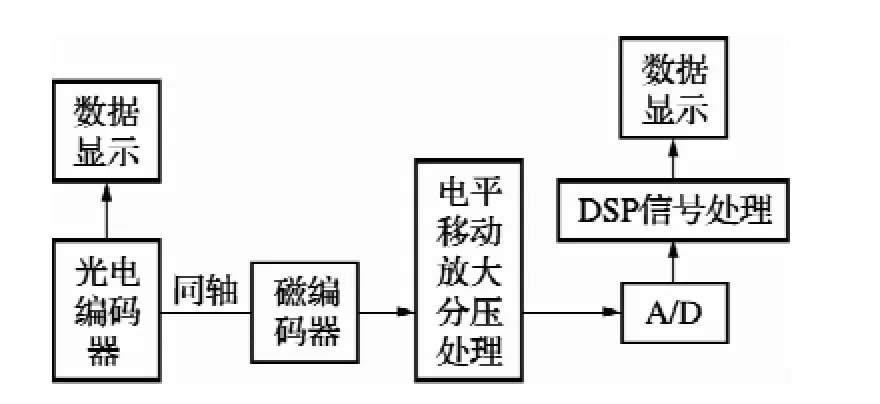
图2 实验系统框图

（2）以光电编码器为基准，在0～360°内均匀选取5个角度采样数据，采用最小二乘法求出最佳的误差补偿系数Ce和De。用高精度光电编码器进行标定，将A／D值和角度值的对应关系制成一个表格，烧录到FLASH存储器中作为查表的数据基准［11］。采用两相电压分区间查表得到角度值，在查表时，引入数据的二插值，可以将分辨率提高一倍，减少比较的次数，节省处理时间，增强了系统的实用性［12］。

（3）按照上述方法进行试验，按椭圆假设求解误差系数，并按式（2）进行误差补偿后，对磁编码器进行了测试，为验证编码器的分辨率，将磁编码器与一个高精度的光电编码器安装在同一个轴上。在低速转动的情况下，观察两编码器输出的角度，结果列于表1。

从表1中可以看出，以高精度的光电编码器作为基准，每隔10°采集数据一次，记录磁编码器的角度值，观察两编码器的角度差，其相对误差在0.15°。

依据椭圆误差补偿算法，用Matlab编写了仿真程序来验证补偿后的角度，并以曲线形式直观表示出来。

对图3、图4进行分析，原始的两路信号合成向量的轨迹圆度误差是3.08左右，经过误差补偿后的两路信号合成向量顶点轨迹的圆度误差是0.32左右，验证了此方法能很好地减小误差。

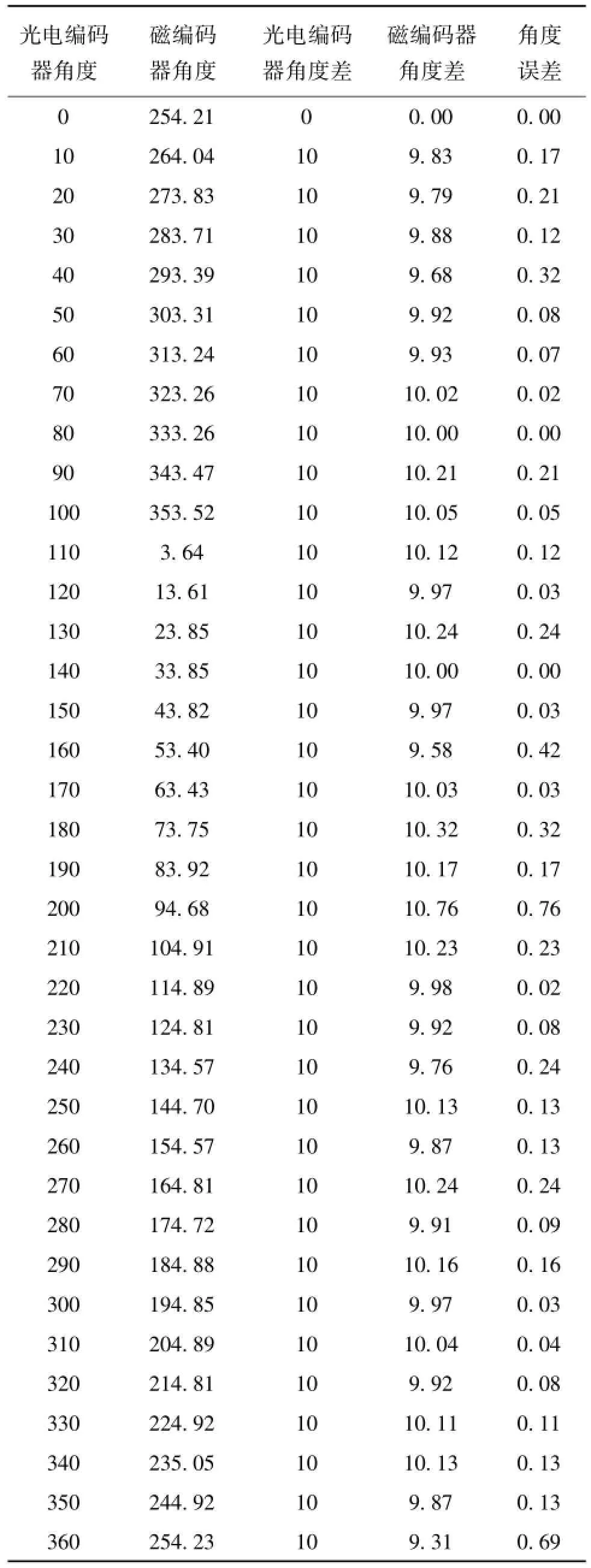
表1 角度测试结果（°）

由图3知，实测的椭圆曲线并不规则。经分析，实验中手动安装永磁体和霍尔元件，不能保证永磁体安装在轴心位置而导致偏心产生，而且两个霍尔元件的安装也不能保证完全正交，从而无法确定霍尔元件如何放置才能通过相同的磁通量，得到两路正交的信号。由于手动采样，采集到有误差的数据绘出不规则的椭圆。使用有误差的数据在离线情况下求解误差系数，得到的误差补偿系数也有一定误差。因此，误差补偿后的曲线如图4所示。

在以后的研究中，要着重研究如何得到高精度的原始数据，进一步提高系统的精度。

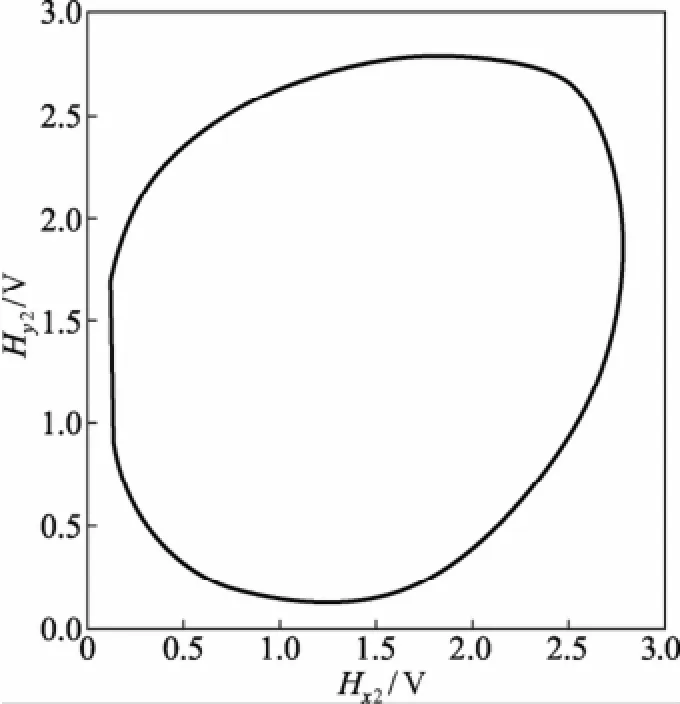
图3 实测曲线

图4 补偿后的曲线

6 结 论

针对单对磁极磁编码器，提出基于椭圆假设的误差补偿方法并采用最小二乘法减小采集数据引起的随机误差。此法无需修改硬件就可实现角度的高精度输出。试验结果表明，在采用12位A／D转换器的前提下，该方法能很好地减小误差，最终实现了分辨率为0.02°的角度输出。若想进一步提高磁编码器的分辨率，可以采用更高精度的A／D转换器。

［1］ 魏海涛，赵来定.一种新型的旋转变压器式轴角编码器［J］.2006，25（4）：58－60.

［2］ 吕德刚，李铁才，杨贵杰.高性能磁编码器设计［J］.仪器仪表学报，2006，27（6）：1347－1350.

［3］ Draxelmayr D，Borgschulze R.A mixed-signal Hall sensor IC with direction detection［C］／／Proceedings of the 28th European Solid-State Circuits Conference，2002.ESSCIRC，2002，627－630.

［4］ 李声晋，周奇勋，卢刚.一种旋转变压器－RDC测角系统的数字标定及补偿方法［J］.微特电机，2007，（6）：26－28.

［5］ 陈棣湘，潘孟春，罗飞路.三维磁敏传感器的设计及误差分析［J］.传感技术学报，2006，19（3）：643－644.

［6］ 徐殿国，王宗培，王雅云.旋转变压器轴角数字转换系统的误差分析［J］.仪器仪表学报，1993，14（3）：232-236.

［7］ Hung Van Hoang，JaeWook Jeon.Signal compensation and extraction of high resolution position for Sinusoidal Magnetic Encoders［J］.InternationalConferenceon Control，AutomationandSystems，2007，17（20）：1368－1373.

［8］ Hung Van Hoang，Jae Wook Jeon.An efficient approach to correct the signals and generate high-resolution orthometric pulse for magnetic encoder［EB］.http：／／ieeexplore.ieee.org／Xplore／guesthome.jsp 2012-10-2.

［9］ 刘诗斌，冯晓毅，李宏.基于椭圆假设的电子罗盘误差补偿方法［J］.传感器技术，2002，21（10）：29－30.

［10］ 宋海明，韩海，赵柏秦，等.霍尔罗盘误差补偿算法及实验分析［J］.传感器与仪器仪表，2008，24（9）：187－188.

［11］ 郝双晖，刘勇，周春蛟，等.基于标定原理的单磁极编码器设计［J］.南京理工大学学报，2005，29（144）：227－228.

［12］ Balemi S，Automatic Calibration Of Sinusoidal Encoder Signals［C］／／Proceedings of the 16th IFAC World Congress，Prague，2005.

Error Com pensation for Single Pair-pole Encoder Based on Ellipse Hypothesis

ZENG Yi-fan， JIANG Fang-fang
（College of Information Science and Engineering，Shenyang University of Technology，Shenyang，Liaoning 110870，China）

An error compensation method for the single pair-pole encoder is studied.For each of the single-pole magnetic encoder，analyzed offset，sensitivity error，quadrature error and ferromagnetic interference error，the expression of each error is obtained.In order to facilitate the error compensation，the expression to describe theerror common to this type is summed up.The formation process of the error can be assumed as the process of changing from circle to ellipse. Therefore the inverse of this process is the same as the process of error compensation.The experimental results show that the accuracy ofmagnetic encoderwhich used thismethod could reach 0.02°，thus the error compensation effect is obvious. The advantages of themagnetic encoder which is applied thismethod are low-cost，high-precision and convenient to use.

Metrology；Magnetic encoder；Error compensation；Ellipse hypothesis；Single pair-pole

TB922

A

1000-1158（2014）02-0108-05

10．3969／j．issn．1000-1158．2014．02．03

2012-09-17；

2012-12-12

辽宁省教育厅科学研究资助项目（2009A550）；沈阳市科技局科学研究项目（F10-205-1-18）

曾一凡（1955－），男，辽宁沈阳人，沈阳工业大学教授，研究方向为微弱信号检测和信号处理。zengyf1234＠yahoo.com.cn