双目立体视觉中特征点三维坐标重构校准研究

韦争亮， 古耀达， 黄志斌， 吴 菁

（广州计量检测技术研究院，广东广州 510030）

双目立体视觉中特征点三维坐标重构校准研究

韦争亮， 古耀达， 黄志斌， 吴 菁

（广州计量检测技术研究院，广东广州 510030）

双目立体视觉是一种商业化较成熟的三维测量技术，左右摄像机内外参数的精确标定是实现三维重构的基础和关键。针对棋盘格和圆点两种标定板图案研究了相应的图像处理技术，实现了标定点的亚像素精度定位及其有效排序。采用基于单映性约束和非线性优化的多视角平面标定算法实现了摄像机光学及空间位置参数求解。用极线约束残差法衡量标定结果的准确度。基于桥式三坐标标准实现标定点三维重构平面度以及多平面空间夹角测量结果的校准，基于光学三坐标标准实现了标定点三维重构空间距离的校准，并分析了校准结果的不确定度。圆标志点三维重构空间距离示值误差为0.029 mm，不确定度U＝24μm（k＝2）。

计量学；三维测量；双目立体视觉；摄像机标定点；三坐标；校准

1 前 言

双目立体视觉采用双摄像机模仿人眼功能，从不同视角获取物体表面信息，利用视差实现物体表面三维重构，是一种较成熟、商业市场较成功的三维测量技术。为了从不同视角二维图像中恢复目标三维信息，必须对左右摄像机的内部光学及相对空间位置参数进行精确的标定，再依据摄像机成像投影数学模型反算出被测物体表面离散目标点的三维坐标。随着双目立体视觉技术在各个领域应用的不断扩展，越来越需要对该种技术三维测量结果的准确度进行可靠的验证与校准。

本文基于图像处理实现圆点或棋盘图案的平面标定块特征点定位及排序，采用文献［1］中基于不同视角平面成像单映射矩阵约束的摄像机内参数求解法，并结合Levenberg-Marquardt非线性迭代从全局意义上优化参数，实现自搭建的双目立体视觉测量系统摄像机标定。最终通过海克斯康Global Advantage桥式三坐标测量机和德国WERTH的VideoCheck UA超高精度复合式光学三坐标两种溯源标准对标定块特征点三维测量结果进行空间多布局的校准。

2 双目立体视觉测量原理

典型的双目立体视觉测量系统［2］如图1所示。对于目标表面上的某个采样点，根据其在两幅图像中的匹配像素点及摄像机标定参数，可以构建两条空间视线求取其三角交会点获得三维坐标。但缺乏纹理的被测目标表面难以实现左右图像的匹配，通常增设一个投影设备将特定编码的结构光投射到物体表面形成匹配特征［3］，从而降低测量难度，提升测量分辨率和准确度。

图1 基于双目立体视觉的三维测量系统

3 摄像机成像模型

摄像机光学成像如图2所示，空间任意一点P与摄像机光心C的连线交成像平面于点p。依据世界坐标系OXWYWZW到摄像机坐标系CXCYCZC的旋转矩阵R及平移向量T（摄像机外参数），按照公式（1）实现P点世界坐标系OXWYWZW三维坐标（XW，YW，ZW）到归一化成像平面二维坐标系oxy的坐标（xu，yu）的转换。其中ri及ti为矩阵R和向量T的元素。矩阵R的元素ri也可采用三个坐标轴旋转角θ，φ，φ来表示。

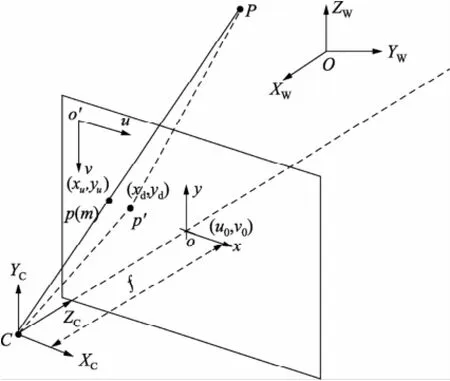
图2 摄像机光学成像

由于制造存在的镜头畸变导致实际像点为p′（xd，yd）。依据公式（2）可实现畸变与非畸变图像坐标转换，其中k1、k2、k3为径向畸变参数，来自透镜形状误差，p1、p2为切向畸变参数，来自透镜组装误差。

最后依据摄像机主点o（光轴与成像平面交点）的对应像素坐标（u0，v0）以及摄像机成像水平和垂直方向以像素为单位的焦距fx、fy，由公式（3）计算出实际像点在计算机屏幕二维坐标系o′uv的坐标（u，v）。

4 标定图像处理及参数求解

首先需要标定板提供一系列分布于测量空间的三维坐标已知的标定点，再通过图像处理提取出标定点在成像平面的二维像素坐标，最后采用特定算法求解摄像机内外参数。采用棋盘和圆点两种图案的平面标定板提供标定输入数据。

图3 棋盘标定板及二值化图像

棋盘标定板的采集图像如图3（a）所示。尺寸为200 mm×200 mm×8 mm，方格数量为13×13个，线间距为12 mm，金属材料。首先进行阈值化分割，得到黑白二值化图像，见图3（b）。Harris定义的角点位于图像二阶导数的自相关矩阵：）

式中：x，y为像素点p的坐标；I为像素灰度值。

有两个最大特征值的地方，在本质上表示以此点为中心周围存在至少两个不同方向的纹理，而棋盘格的角点为4条黑白跳跃清晰边界的交会之处，基于该种角点定义可有效实现棋盘格角点定位［4］。根据边界点与角点连线垂直于边界梯度的约束迭代实现角点的亚像素精确定位，见图4。最后依据棋盘角点上下左右连续位置关系实现所有角点的排序，见图5（a）、（b）。

图4 亚像素定位垂直约束

圆点标定板的采集图像如图6（a）所示，尺寸为400 mm×300 mm×10 mm，圆点数量为11×9个，点间距为25 mm，大圆直径为15 mm，小圆直径为7.5 mm，金属材料。同样，首先将图像二值化分割出目标圆点，见图6（b），提取跟踪所有黑白跳跃的连续边界。摄像机透视成像后标准圆点变成了椭圆形状，用最小二乘法拟合封闭边界椭圆系数，通过拟合误差阈值（小于5个像素值）可有效排除各类非目标椭圆点边界，见图6（c）、（d）。沿着有效的椭圆边界点梯度方向最小二乘拟合抛物线峰值点定位亚像素边界点，再次拟合椭圆系数实现亚像素级别的椭圆中心点定位。根据面积差别提取出4个大点，由距离最短的两个连续大点确定X轴排列方向，依据其它大点与X轴大点的夹角确定Y轴及各轴正负方向，以4个大点为出发点，依据上下左右连续位置约束搜索定位出99个标定点并排好次序，见图6（e）、（f）。

图5 棋盘角点定位实例

图6 圆点标定板圆心定位实例

摄像机标定参数求解方法主要有线性模型方法、非线性法、基于径向约束的Tsai两步法［5］、畸变参数预矫正法、神经网络方法、局部逐点单像素方法［6］。文献［1］对参数求解及优化步骤进行了详细介绍，提出的多位置平面标定方法只需单平面标定块，操作灵活方便，标定成本低，随意放置无需精密位移装置，测量空间覆盖充足，参数求解精度较高，应用较为广泛。

数学模型线性变换公式如下：

式（6）为矩阵代号缩写式：

将世界坐标系XY平面设置于标定板平面上，则M＝[XWYW0 1]，标定板平面二维坐标点M与对应图像二维坐标点m间存在一个单应性矩阵变换H。

依据公式（7）建立的方程组可以解算出每一个标定位置的H，基于式（8）和R的正交性（），可得到两个关于摄像机内参数的基本约束方程

理论上获取3个以上视角，即3×2个内参数约束即可通过奇异值分解和Cholesky矩阵分解算法实现内参数矩阵的唯一确定。求解出内参数矩阵A之后，每个标定位置的外参数矩阵即可按下式求解

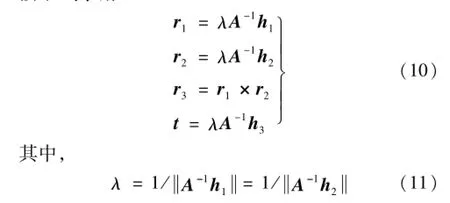
为了提高标定精度，必须考虑客观镜头畸变问题。以实际检测图像坐标m与由参数初值算出的图像坐标的残差平方和

为目标函数，用Levenberg-Marquardt法进行非线性迭代，全局优化参数。

5 三维测量结果校准

双目立体视觉成像存在极线几何约束。如图7所示，左右图像极线由双摄像机的光心及空间点确定的光平面与成像平面的相交而形成。左图像的某像素点在右图像上的匹配点必定位于其对应极线上，相反亦成立。由摄像机标定内外参数求解基本矩阵F，可建立极线约束方程：

式中：mTr表示右图像像素坐标；ml表示左图像像素坐标。

摄像机标定准确度最直接的一种衡量参数就是所有左右图像标定点去除镜头畸变后与其对应极线的距离偏差均值。

图7 外极线几何

图8 棋盘格标定板图像集

图8给出了3个不同空间位置的棋盘格标定板采集图像。一共采集了10个不同视角的数据进行摄像机标定。标定后极线距离偏差均值为0.099 pixel。图9为非标定位置的棋盘格144个标定点的三维重构结果。图10为空间点最小二乘平面拟合距离偏差示意图，平面拟合的偏差均值为0.05 mm，正负距离偏差的最大间隔即平面度为0.29 mm。棋盘格标定板采用桥式三坐标标准测量得到的平面度参考值为0.053 mm。采用光学三坐标测量得到的棋盘格标定板邻接角点的距离均值为11.907 mm，实测连续角点距离均值为11.961 mm。表1为其中5个连续角点的空间坐标及距离测量结果。

图11为4个不同空间位置的圆点标定板采集图像。同样共采集10个视角数据，极线距离偏差均值为0.096 pixel。99个圆心标定点三维重构结果如图12，最小二乘平面拟合距离偏差示意如图13所示。平面拟合误差均值0.045 mm，平面度为0.328 mm，桥式三坐标平面度标准值0.027 mm，光学三坐标连续圆点距离标准均值为24.976 mm，连续圆点距离均值实测值为25.005 mm。

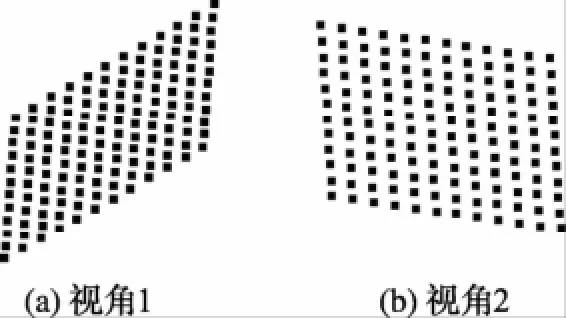
图9 棋盘角点三维重构结果

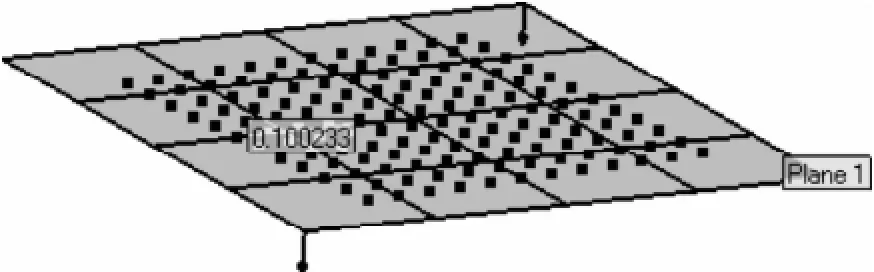
图10 144点平面拟合误差示意图

表1 5个角点空间坐标及距离实测结果mm

图11 圆点标定图像集

将棋盘标定板放置于3个不同空间位置测量，图14为重构结果三维显示图。基于桥式三坐标得到任意两个空间位置平面夹角，共3个角度标准值和三维重构的3个角度实测量值，见表2，最大角度误差为－0.061°。

图12 99个圆心点三维重构结果

图13 圆心最小二乘平面拟合距离偏差示意图

图14 3个不同位置平面的三维重构结果

表2 平面间夹角测量结果

6 校准不确定度分析

对邻接圆心距离均值三维测量示值误差进行不确定度分析。

空间距离示值误差e为实测值lm与光学三坐标标准值ls之差。

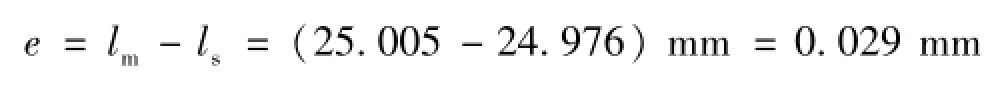
（1）标准不确定度分量u（lm）为圆心距离均值三维测量重复性，具体结果见表3。共测量10次，标准偏差为0.012 mm。

表3 距离均值重复性测量结果mm

（2）不确定度分量u（ls）由标准器光学三坐标测量的最大允许误差MPE引入。按均匀分布计算，则

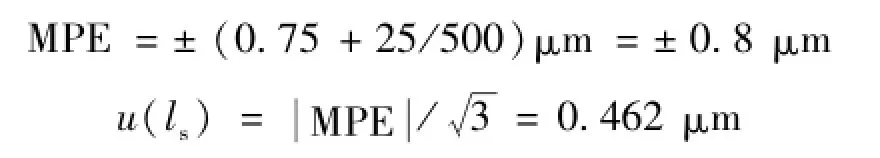
合成标准不确定度［7］：

取包含因子k＝2，U＝24μm。

采用WERTH VideoCheck UA光学三坐标溯源标准，与同类型设备相比具有较高精度，但考虑测量成本及可行性，可选用普通的视频影像测量仪标准，若其最大允许误差为±5μm，按照上述评定过程计算到的U为25μm，依据不确定度小于等于被评定测量仪器最大允差1／3的要求，可满足允差大于0.075 mm的三维重构校准。

7 结 论

基于图像二值化、梯度边界提取跟踪、形状约束、最小二乘拟合等图像处理技术实现棋盘或圆点平面标定块特征点识别及亚像素精度定位。基于单映性约束多视角平面标定算法实现摄像机内部光学及相对空间位置外参数求解，通过非线性迭代优化解算镜头畸变参数，采用桥式三坐标和光学三坐标标准对非标定位置的平面特征点三维测量结果进行校准。

棋盘格角点平面范围为132 mm×132 mm，三维重构的平面拟和误差为0.051 mm，平面度测量示值误差为（0.290－0.053）mm＝0.247 mm，误差相对整个平面范围为1.9×10－3，空间距离示值误差为（11.961－11.907）mm＝0.054 mm，误差相对整个平面范围为0.4×10－3。

圆点平面范围为250 mm×200 mm，三维重构平面拟和误差为0.045 mm，平面度测量误差为（0.328－0.027）mm＝0.301 mm，误差相对测量范围为1.2×10－3，空间距离示值误差为（25.005－24.976）mm＝0.029 mm，误差相对测量范围为0.1×10－3。

从实验结果相对于整个测量范围的误差可以看出：圆点标定的准确度高于棋盘标定，主要是因为圆心标志点在数字图像中的唯一确定性高于棋盘角点。由于制作因素，在光学三坐标的放大镜头中可看到形成棋盘格角点的4条边界交会并未对齐，实际交会角点是个空白区域，导致其定位精度低于可依据边界精确定位的圆心特征。

空间距离的示值误差较明显地小于平面度的误差，说明所采用的参数求解方法没有较好符合标志点来自于同一平面的约束，设定的标定点距离约束则得到了较好符合。

三维重构的测量误差除了来自特征点的图像定位算法、摄像机标定算法、标定板的制作精度以外，图像采集硬件的性能也将会直接影响三维测量的精度。由于本文采用的三维测量校准技术是在基础的摄像机标定层面上进行，因此有助于更直接发现测量误差的来源。

［1］ Zhang Z Y.A Flexible New Technique for Camera Calibration［J］.IEEEtransactionsonpatternanalysisand machineintelligence，2000，22（11）：1330－1334.

［2］ 张广军.机器视觉［M］.北京：科学出版社，2009，99－108.

［3］ 谢捷如，王震.运用LCD条纹投影进行光学三维轮廓测量［J］.计量学报，2008，29（4）：301－304.

［4］ Bradski G，Kaebler A.学习OpenCV［M］.于仕琪，刘瑞祯，译.北京：清华大学出版社，2009.

［5］ Tsai R Y.A Versatile Camera Calibration Technique for High-Accuracy 3D Machine Vision Metrology Using Offthe－shelf TV Cameras and Lenses［J］.IEEEjournalof roboticsandautomation，1987，RA－3（4）：323－344.

［6］ Liu H Y，Su W H，Richard K，etal.Calibration-based phase-shifting projected fringe profilometry for accurate absolute 3D surface profile measurement［J］.Optics Communications，2003，216，（1－3）：65－80.

［7］ 国家质量监督检验检疫总局.JJF 1059.1—2012，测量不确定度评定与表示［S］.2012.

Research on Calibration of Three Dimensional Coordinate Reconstruction of Feature Points in Binocular Stereo Vision

WEIZheng-liang， GU Yao-da， HUANG Zhi-bin， WU Jing
（Guangzhou Institute of Measuring and Testing Technology，Guangzhou，Guangdong 510030，China）

Binocular stereo vision is one of the 3D measurement techniques which is more adult in commerce.The accurate calibration of inner and out parameters for left and right camera is basic and important in realizing 3D reconstruction.Corresponding image process techniques to two calibration block pattern with chess corners or circle points are researched，so the feature points are located in sub-pixel accuracy and effectly sequenced.The optical and space parameters are calculated by calibration algorithm of homography constraint and multe-view plane.Accuracy of calibration result is evaluated by epipolar constraint residualerror.The calibration ofmeasurement results of flatness and angle between planes of feature points 3D reconstruction is completed by standard of bridge CMM.The calibration of space distance of feature points is completed by standard of optical CMM，and the uncertainty is analyzed.The indication error of space distance of circle calibration points 3D reconstruction is 0.029 mm，uncertaintyUis 24μm（k＝2）.

Metrology；Three dimensional measurement；Binocular stereo vision；Camera calibration point；Coordinatemeasuringmachining；Calibration

TB921

A

1000-1158（2014）02-0102-06

10．3969／j．issn．1000-1158．2014．02．02

2013-05-27；

2013-07-04

国家质检总局科技计划项目（2012QK063）

韦争亮（1982－），男（壮族），广西河池人，广州计量检测技术研究院工程师，博士，主要从事几何量计量、非接触光学三维测量技术研究。2609517012＠qq.com