基于经验模态分解样本熵的肌电信号识别

席旭刚， 朱海港， 罗志增， 张启忠

（杭州电子科技大学智能控制与机器人研究所，浙江杭州 310018）

基于经验模态分解样本熵的肌电信号识别

席旭刚， 朱海港， 罗志增， 张启忠

（杭州电子科技大学智能控制与机器人研究所，浙江杭州 310018）

针对表面肌电信号非线性、噪声强等特点，设计一种快速有效的表面肌电信号手部多运动模式识别方法，用于肌电假手的实时控制。提出了一种基于经验模态分解样本熵和聚类分析的表面肌电信号多运动模式识别方法。该方法对动作持续阶段的信号首先进行经验模态分解，将其分解为多个平稳的固有模态函数（IMF），再依据频率有效度选取若干个包含肌电信号有效信息的IMF分量求和后，计算其样本熵。以尺侧腕伸肌和尺侧腕屈肌两路肌电信号对应的EMD样本熵作为特征向量，设计了主轴核聚类算法的聚类分类器进行模式识别。成功识别了展拳、握拳、腕上翻和腕下翻4种动作，平均识别率达到93%。该方法取得了较高的识别率，抗干扰能力强，计算量少，可用于肌电假手的控制。

计量学；表面肌电信号；经验模式分解；样本熵；聚类分析；模式识别

1 引 言

表面肌电信号（Surface electromyography，sEMG）是从人体骨骼肌表面通过表面肌电拾取电极记录下来的、与神经肌肉活动相关的生物电信号，其中蕴含着很多与肢体运动相关联的信息［1］，不同的肢体动作具有不同的肌肉收缩模式，肌电信号特征也将有所差异，通过对这些特征的分析就可以区分肢体的不同动作模式，因此，它不仅被广泛运用于临床诊断、运动医学等领域［2～4］，还成为残障人士假肢的理想控制信号［5］。随着对肌电信号产生机理的研究，研究者们发现sEMG具有非周期、非平稳、非线性等混沌特性［6～8］，近年来运用非线性指标来识别动作表面肌电信号的模式也得到了深入地研究，如王人成［9］等利用Hausdorff维区别了伸腕、屈腕和旋腕3个动作；Hu X［10］等利用GP算法的信息维识别了腕正旋、腕反旋2个动作；邹晓阳、雷敏［11］等将最大李雅普诺夫指数和多尺度分析方法结合起来，然后利用支持向量机较好地识别了人体前臂的内翻、外翻、握拳、展拳、上切和下切6类动作；澳大利亚皇家墨尔本理工大学的Arjunan S P，Naik G R等［12～15］提取手部各类动作的肌电信号的分形维特征，然后结合支持向量机识别手部各个动作，取得了较高的识别率。这些非线性算法均较好地解决了肌电信号的特征提取问题，然而这些特征提取方法需要长时间稳定的sEMG信号，抗噪能力较弱，对肌电假手就不能较好地实时控制。

本文提出了一种将经验模态分解（Empirical mode decomposition，EMD）与样本熵相结合的特征提取方法——EMD样本熵，首先将sEMG信号进行经验模态分解，选取若干个包含肌电信号有效信息的固有模态函数（Intrinsic Mode Function，IMF）分量求和作为有效肌电信号，求取其样本熵，然后将样本熵作为特征向量，运用主轴核聚类分类器有效地区分了腕上翻、腕下翻、展拳和握拳4类动作。实验表明，该方法取得了较高的识别率，抗干扰能力强，计算量少，可用于肌电假手的控制。

2 基本原理

2.1 经验模态分解

经验模态分解（EMD）是一种新出现的信号分析方法［16］，它将信号自适应地分解到不同的尺度上，非常适合非线性、非平稳信号的处理，不仅具有小波分析的全部优点，还有更清晰准确的谱结构，因而引起了信号处理相关领域的极大兴趣，并广泛应用于工程领域［17，18］。它基于一个基本的假设条件，即所要分析的信号是由许多不同的固有模态函数（IMF）相互叠加而成。不同时间尺度的各种模式将会根据其自身的特征尺度进行分解，分解后的每种模式是相互独立的，在连续的过零点间不存在其他

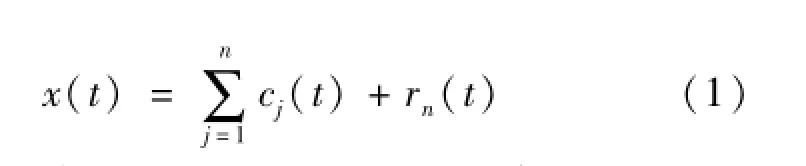
式中，cj（t）为第j个IMF分量；rn（t）为余项。

信号在分解的过程中保留了原来的特性，这些IMF分量频率从大到小，包含着不同的特征时间尺度，将信号的特征信息在不同的分辨率下表现出来，从而可以选取信号的IMF分量组成新的特征信息。

自适应地选取前若干个IMF分量，本文采用了基于瞬时频率的有效信息统计法，定义第i层的内蕴模式分量IMFi的频率有效度Ei＝ni／n。其中，ni为IMFi中瞬时频率落在20～350范围内的点数，n为总的信号采样点数，Ei为在指定频率段的有效信息量。由于EMD分解的各层IMF分量的频率逐层减小，它们的频率有效度也各不相同，因而通过设定频率有效度Ei的值可以选取不同的若干个IMF分量。

2.2 样本熵

样本熵是在近似熵的基础上，Richman［19］提出的一种改进的时间序列复杂度测量方法。它与近似熵类似但精度更好，不但具备近似熵的所有优点，而且避免了近似熵中统计量的不一致性，具有其他非线性动力学参数所不具有的优点。样本熵计算所需数据短，算法的运算量小，只需要很短的数据（100～5 000点）便可得到稳健的样本熵估计值，不依赖于数据长度；样本熵具有很好的一致性，即如一时间序列比另一时间序列有较高的样本熵值的话，那么不管它们的维数和相似容限如何变化，这一结论不会变化；样本熵对于丢失数据不敏感，即使丢失多达1／3，对样本熵的值影响依然很小；这些特点对需要实时控制的肌电假手应用非常重要，而其他一些非线性参数（关联维数、李雅普诺夫指数等）的计算却需要大量的数据，算法的时间复杂度与空间复杂度大；另外样本熵表示非线性动力学系统产生新信息的速率，样本熵值越低，序列的自我相似性极值点。所以每一个IMF均要满足以下2个判断条件：整组IMF数据中极值点和过零点的数目相等或最多相差1；信号的局部极大值包络线和局部极小值包络线的均值为0。根据这2个条件对信号不断的“筛选”，可以将任意非线性、非平稳信号自适应的分为若干个不同的内蕴模式函数（IMF）和1个剩余分量。越高，产生新模式的速率也就越低，样本熵值越大，表示序列越复杂。因此样本熵非常适合肌电信号非线性特征的分析，本文采用的是样本熵的快速算法［20］，在保持样本熵优点的情况下，计算速度更快。

快速样本熵的计算步骤如下：

（1）设肌电信号时间序列｛xi｝含有N个数据，分别为x（1），x（2），…，x（N）。

（2）将序列｛xi｝按顺序组成一组m维矢量

矢量X（i）与X（j）之间的距离dis［X（i），X（j）］用分量间的最大欧氏距离表示，即

（3）定义N×N的二值距离矩阵为D，D的第i行第j列为dij，给定阈值r（r＞0），则

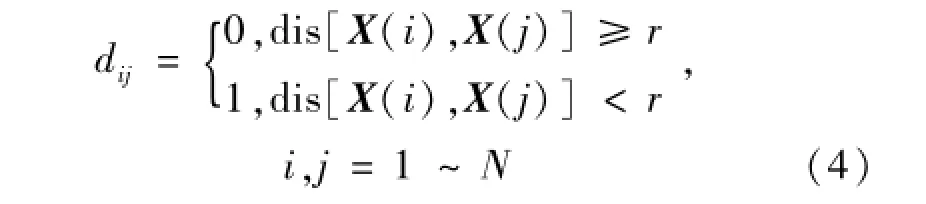
（4）利用矩阵中的元素计算Bmi（r）和Bm＋1i（r）

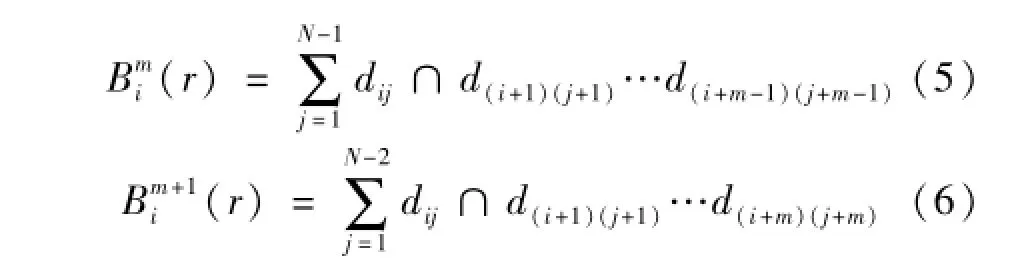
（5）求所有的Bmi（r）的平均值记为Bm（r）及Bm＋1i（r）的平均值记为Bm＋1（r）

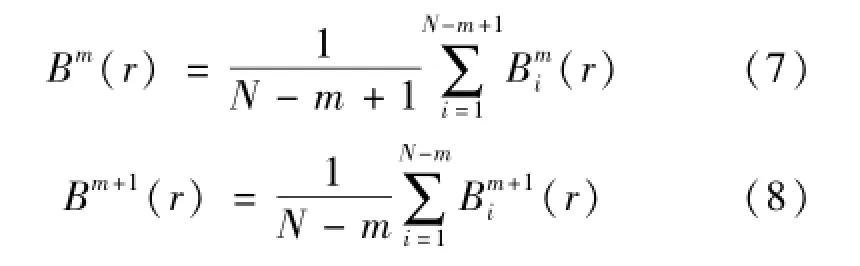
（6）肌电信号时间序列x{}i的样本熵Esamp可表示为

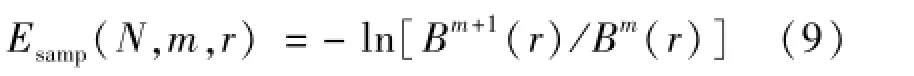
样本熵值显然与嵌入维数m和相似容限r的取值有关，在一般情况下，m取1或2，r取0.1～0.25倍的数据标准差。m的取值越大，算法所需要的数据量越大，计算时间也就越长；r取值越大，时间序列的细节信息损失越多，r取值越小，噪声对结果的影响越显著。通过取不同的m和r值计算肌电信号的样本熵值，大量实验证明当m不变时，r从0.1～0.25变化时，样本熵值成减小趋势，但变化很微小，对特征提取的影响不大，因此本文取m＝2，r＝0.2，特征提取的效果也较为理想。

2.3 主轴核聚类算法

根据肌电信号样本熵分布特征，本文设计了一种基于样本与核的相似性度量的算法——主轴核聚类算法，该算法和K均值算法原理相似，均为核聚类算法的一种，但它们选取的核函数不同，在K均值算法中，用样本均值替代了核函数，因此每类样本仅用一个聚类中心来作为一类的代表，而一个点往往不能够充分地反应出该类的样本分布结构，当类的分布是球状或近似球状时，即每类中各分量的方差接近相等时，K均值算法分类效果较好，但形状发生变化时，就会影响分类的效果。而主轴核聚类算法用一个聚类主轴作为一类的代表，不仅能对类的自然分布为球状或接近球状的样本作有效分类，还能够对一些分布为非球状的样本尤其是那些椭球或近似椭球状的样本作出更有效地分类，算法思想简便，容易实现。

设一个d维矢量样本集X＝｛x1，x2，…，xn｝，类别数为c，定义主轴核函数为

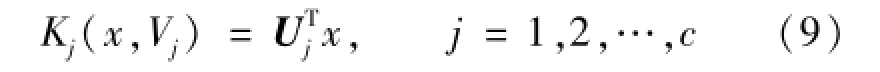
任一样本x与一个轴Uj之间的相似程度可以用x与wj类主轴之间的欧氏距离的平方来度量

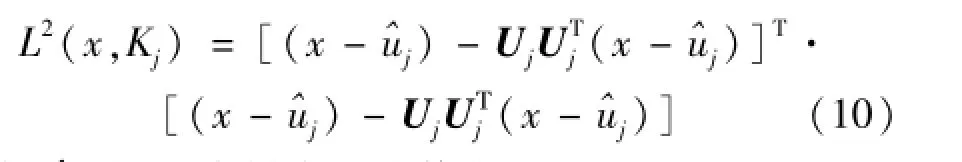
式中，＾ui为wj类样本的均值向量。

任一样本与某个类主轴的欧氏距离不受特征量纲选取的影响，并且平移不变，而且也反应了特征的相关性。通过对训练数据的聚类分析，用已知动作训练集分别求取的每个动作的主轴核函数为相应类的聚类主轴，每个聚类主轴均为一个d维矢量。如果给定矢量属于第j类，那么它到第j类聚类主轴的欧氏距离最小；因此，如果要判定矢量属于哪一类，只要计算它到哪一类聚类主轴的欧氏距离最小即可。

3 实验研究

3.1 信息预处理

实验采用美国Noraxon公司的mt400肌电信号采集仪，先用酒精分别在受试者的尺侧腕伸肌和尺侧腕屈肌上擦涂去污，以增强信号的拾取能力，然后将一次性肌电电极贴于受试者的前臂尺侧腕伸肌和尺侧腕屈肌处，用于采集表面肌电信号。把肌电信号采集仪（采集频率1 000 Hz）的输出通过蓝牙USB连接到装有肌电处理软件的计算机上，肌电处理软件获取的手部动作肌电信号采样值以Matlab文件的格式导出，采集腕上翻、腕下翻、展拳和握拳共4种手前臂动作的表面肌电信号各80组，共320组数据。肌电信号采集仪内置截止频率500 Hz的低通滤波器和截止频率为10 Hz的高通滤波器，消去了大部分的噪声。图1为采集到的展拳动作表面肌电信号。

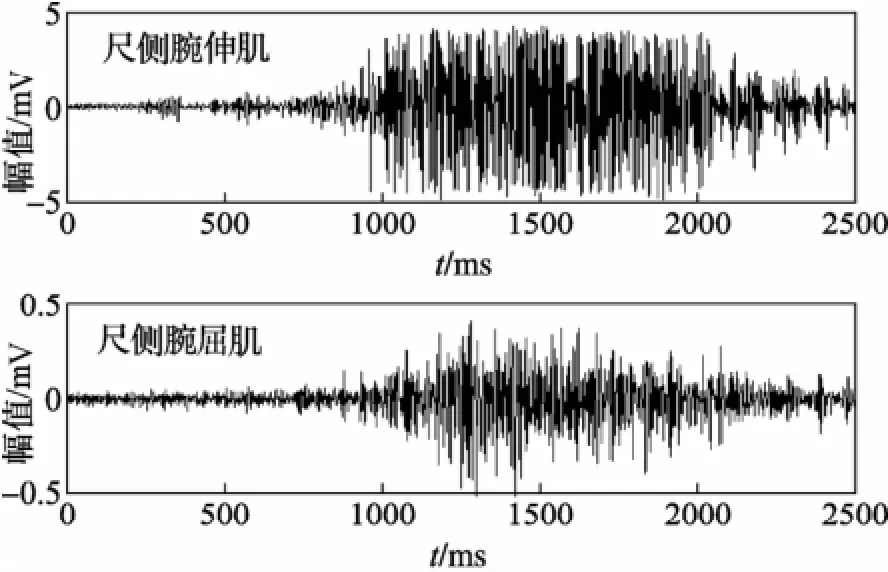
图1 展拳动作表面肌电信号

3.2 肌电信号特征提取与分析

特征选取是模式识别的核心问题，它不仅影响分类器的设计，还关系到分类的有效性。如果不同类别的特征差别较大，就比较容易设计分类器把各个类别很好地识别出来。为了验证样本熵在表面肌电信号中的有效性，分别对采集的4类动作中每组肌电信号的尺侧腕伸肌和尺侧腕屈肌信号各20组数据进行处理，由于在熵的理论中，正确判断动作的起始位置和终止位置是熵值能否成功区分动作的关键，因此本文在这里运用能量阈值确定动作的起始位置和终止位置［21］，通过计算发现每种动作约有1 000个样点。对表面肌电信号分别进行如下处理：（1）对动作信号直接求近似熵和样本熵；（2）对动作信号进行EMD分解，把分解后的各个IMF分量和包含主要信息的前若干个IMF分量之和作为肌电信号求近似熵和样本熵。

经过大量实验观察它们的特征分布发现：无论是对动作信号直接求近似熵还是对经EMD分解后的IMF分量求近似熵均发生模态混叠，而对动作信号求取的EMD样本熵聚类性较好。EMD分解后的各个IMF分量与前若干个IMF分量之和的样本熵的聚类性不一。其中当Ei＞60%时，满足频率有效度的前5个IMF分量之和的样本熵聚类性最好，因此本文采用对表面肌电信号进行EMD分解后，依据频率有效度的方法对选取的前5个IMF分量进行迭加作为动作信号求取样本熵进行特征提取，将EMD样本熵方法与直接进行样本熵特征提取的方法进行对比，以屈肌样本熵为横坐标，伸肌样本熵为纵坐标建立直角坐标系，它们的特征分布结果见图2、图3。并计算各自的均值和标准差，结果见表1。

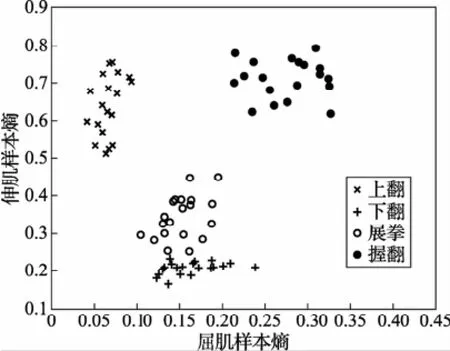
图2 表面肌电信号样本熵分布

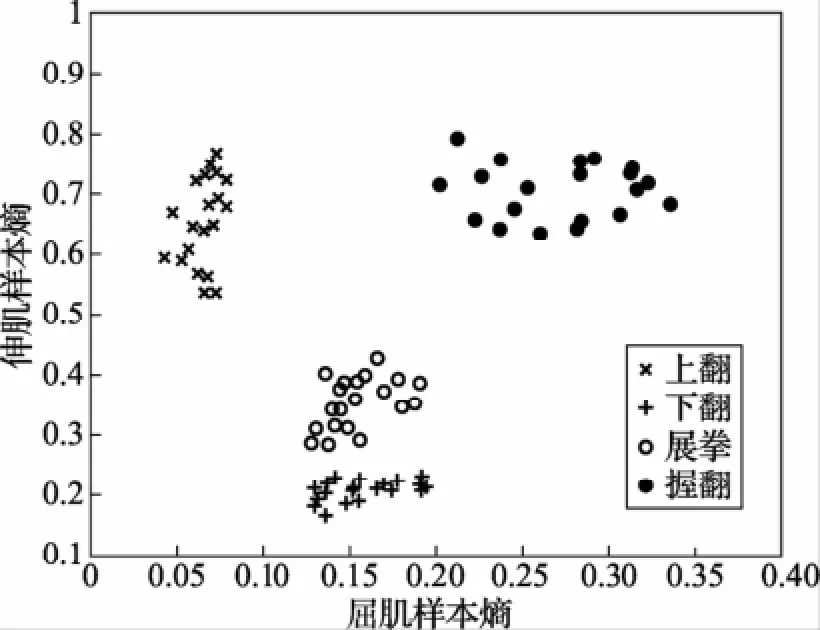
图3 表面肌电信号EMD样本熵分布

由图2、图3可以看出，EMD样本熵和直接样本熵具有相似的分布，不同动作在平面上有着相对独立的聚类区域，类区分性较好；但通过对比表1和图2、图3发现，EMD样本熵相对于直接样本熵来说标准差系数较小，聚合度更大，类区分性更好，所以更容易达到理想的分类结果。

3.3 模式分类

在模式识别的过程中，分类器的性能决定了分类效果的有效性，根据样本熵较好的聚类分布特点，并且各个动作的分布区域近似于椭球状，所以本文采用了核聚类算法，并分别选用了主轴核函数和正态分布的核函数进行核聚类分析，通过实验证明采用主轴核函数的分类效果较好。

采集的每个动作的表面肌电信号均有屈肌和伸肌两路信号组成，所以对每组信号求取样本熵均会产生屈肌样本熵和伸肌样本熵，将每组动作的屈肌和伸肌的样本熵构成特征向量A＝［xi，yi］，其中xi为第i组屈肌信号的样本熵值；yi为第i组伸肌信号的样本熵值。选取采集的每类动作信号的40组共160组表面肌电信号作为训练集，通过求取样本熵和EMD样本熵两种方法分别获得各自的特征向量，利用主轴核聚类算法分别求取各个特定动作的主轴核函数，然后将剩下的160组数据作为测试集，送入主轴核聚类分类器进行识别，若识别结果与测试目标一致，说明对测试的动作进行了正确归类，否则是错误归类，两种方法的识别结果见表2。

表1 4种手部动作肌电信号的样本熵和EMD样本熵统计特性（均值±标准差）×10－2

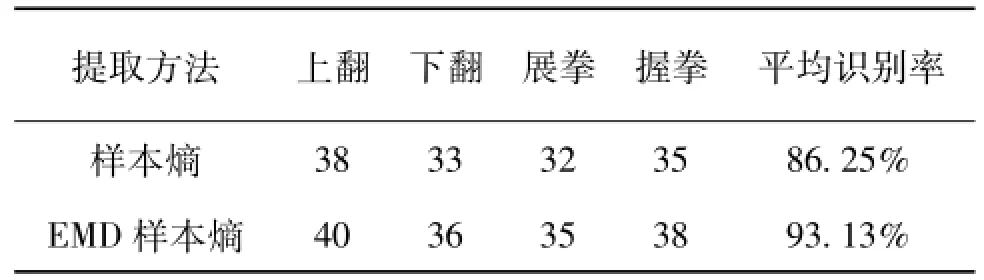
表2 两种特征提取方法的手部动作识别结果

由表2可以看出，样本熵可以有效地区分手部肌电信号的上翻、下翻、展拳、握拳4个动作，识别率分别为95%、82.5%、80%、87.5%，平均识别率达到了86.25%；而EMD样本熵算法对4种动作的识别率分别为100%、90%、87.5%和95%，平均识别率达到了93.13%，明显优于直接样本熵方法，分类效果较好，这是由于sEMG信号经过EMD分解选取若干IMF分量之和，摈弃了大量冗余信息，使EMD样本熵算法具有良好的抗干扰性，更适用于肌电信号的特征提取。

本文也尝试用其他模式分类器，由于EMD样本熵有着良好的聚类分布，所以本文选取了另外两个常用的聚类分类器：基于K均值的聚类分类器和基于距离测度的马氏距离分类器作为对比，它们均选择已知动作训练集的特征矢量的均值作为每个动作的聚类中心，然后对测试集进行分类识别，训练集为每类动作信号的40组共160组表面肌电信号，测试集为剩下的160组数据，识别结果见表3。

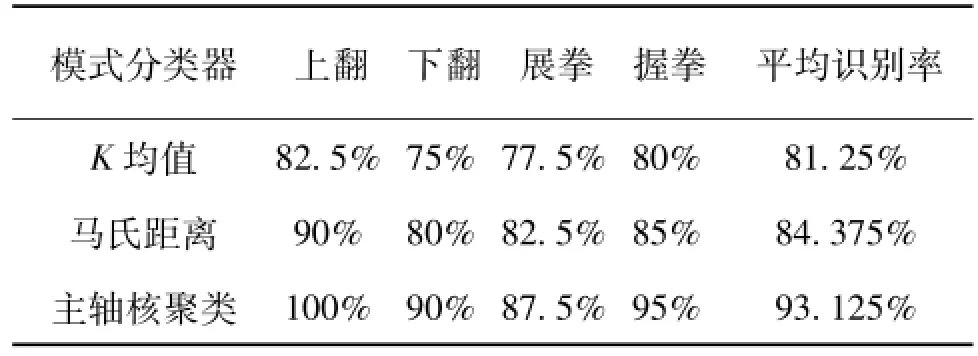
表3 不同的分类器的识别效果

由表3可以看出，主轴核聚类算法明显优于K均值算法和马氏距离算法，主要原因是前两种算法适合那些类的自然分布为球状或近似球状的样本作有效聚类，而EMD样本熵的聚类分布近似椭球型，本文所提出的主轴核聚类算法比较适合这种特征分布的分类，取得了较为理想的分类效果。

4 结 论

本文运用EMD样本熵对腕上翻、腕下翻、展拳和握拳4类手部动作的尺侧腕伸肌和尺侧腕屈肌两路表面肌电信号进行了分析。研究表明，样本熵能够从较短的时间序列中揭示动作表面肌电信号的复杂性，很好地表现肌电信号的细微变化情况，抗干扰能力强，算法简单，计算速度较快，特别适合肌电信号的实时处理。而对sEMG信号进行EMD分解后，利用样本熵对包含肌电信号主要信息的前若干个IMF分量进行复杂度分析的方法，很好地去除了肌电信号中的冗余信息，能够得到更好的样本熵特征分布，最后根据EMD样本熵的聚类分布近似椭球型分布的特点，利用主轴核聚类算法对4类前臂动作进行分类，取得了较为理想的效果。

［1］ De Luca C J.Physiology and mathematics ofmyoelectric signals［J］.IEEE Trans Bio Med Eng，1979，26（6）：313－325.

［2］ Hoover CD，Fulk G D，Fite K B.The Design and Initial Experimental Validation of an Active Myoelectric Transfemoral Prosthesis［J］.Journal Medical Devices，2012，6（1）：011005－12.

［3］ 吴小鹰，侯文生，郑小林，等.腕长伸肌表面肌电与握力大小的相关性研究［J］.仪器仪表学报，2008，29（8）：1605－1608.

［4］ 高云园，佘青山，孟明，等.基于多源信息融合的膝上假肢步态识别方法［J］.仪器仪表学报，2010，31（12）：2682－2688.

［5］ 席旭刚，李仲宁，罗志增.基于相关性分析和支持向量机的手部肌电信号动作识别［J］.电子与信息学报，2008，30（10）：2315－2319.

［6］ 张启忠，席旭刚，高发荣.采用匹配滤波和ICA消除sEMG的工频干扰［J］.计量学报，2013，34（2）：168－172.

［7］ LeiM，Wang Z Z，Feng Z J.Detecting nonlinearity of action surface EMG signal［J］.Phys Lett A，2001，290（5－6）：297－303.

［8］ 刘加海，王丽，王健.基于相空间、熵和复杂度变化的表面肌电信号分析［J］.浙江大学学报（理学版），2006，33（2）：182－186.

［9］ 王人成，黄昌华，常宇，等.表面肌电信号的分形分析［J］.中国医疗器械杂志，1999，23（3）：125－127.

［10］ Hu X，Wang Z Z，Ren X M.Classification of surface EMG signal with fractal dimension［J］.J Zhejiang Univ Sci B，2005，6（8）：844－848.

［11］ 邹晓阳，雷敏.基于多尺度最大李雅普诺夫指数的表面肌电信号模式识别［J］.中国生物医学工程学报，2012，31（1）：7－12.

［12］ Arjunan SP，Kumar D K，Naik G R.Features of sEMG based on source separation and fractal properties to detect wrist movements［J］.Biomed Eng Appl Basis Commun，2010，22（4）：293－300.

［13］ Naik G R，Kumar D K，Arjunan S P.Towards classification of low-level fingermovements using forearm muscle activation：A comparative study based on ICA and Fractal theory［J］.Int JBiomed Eng Technol，2011，6（2）：150－162.

［14］ Arjunan S P，Kumar D K，Naik G R.A machine learning basedmethod for classification of fractal features of forearm sEMG using twin support vector machines［C］／／Annual International Conference of the IEEE on Engineering in Medicine and Biology Society，Buenos Aires，2010.

［15］ Arjunan S P，Kumar D K，Naik G R.Fractal based modelling and analysis of electromyography to identify subtle actions［C］／／Annual International Conference of the IEEE on Engineering in Medicine and Biology Society，Lyon，2007.

［16］ Huang N，Shen Z.The Empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc R Soc Lond A，1998，454（1971）：903－995.

［17］ Taheri F.Damage identification in beams using empiricalmode decomposition［J］.Struct Health Monit，2011，10（3）：261－274.

［18］ 聂永红，程军圣，张亢，等.基于EMD与响度的有源噪声控制系统［J］.仪器仪表学报，2012，33（4）：801－808.

［19］ Richman J S，Moorman JR.Physiological time-series analysis using approximate entropy and sample entropy［J］.Am J Physiol-Heart and Circulatory Physiol，2000，278（6）：H2039－H2049.

［20］ 王新沛，杨静，李远洋，等.基于样本熵快速算法的心音信号动力学分析［J］.振动与冲击，2010，29（11）：115－118.

［21］ 雷敏，王志中.一种用于实时提取动作信号的新方法［J］.中国医疗器械杂志，2000，24（4）：200－202.

EMG Signal Recognition Based on EMD Sam ple Entropy

XIXu-gang， ZHU Hai-gang， LUO Zhi-zeng， ZHANG Qi-zhong
（Intelligent Control＆Robotics Institute，Hangzhou Dianzi University，Hangzhou，Zhejiang310018，China）

According to the chaotic and nonlinear characteristics of surface electromyography（sEMG），a fast and efficient handsmovement sEMG pattern recognitionmethod for real-time control ofmyoelectric prosthetic hand is designed.A multi-modeling pattern recognition method of sEMG features based on the empirical mode decomposition（EMD）sample entropy and clustering analysis is proposed.First，it decomposes the sEMG signal into a set of intrinsic mode functions（IMF），then combines some of the IMF which contains the useful information according to frequency effectiveness，and calculates the sample entropy of the combination.The sample entropy of two sEMG of the extensor carpi ulnaris and flexor carpi ulnaris constitute the feature vector，the clustering classifier which based on principal axis clustering arithmetic is applied to classify the four hand movements.The result shows that four movements（hand extension，hand grasps，wrist spreads and wrist bends）are successfully identified.The average recognition rate is 93%.The method achieved high recognition rate，anti-interference ability and less computation，that is suitable for the control of themyoelectric prosthetic hand.

Metrology；Surface electromyography；Empiricalmode decomposition；Sample entropy；Clustering analysis； Pattern recognition

TB973

A

1000-1158（2014）06-0534-06

10．3969／j．issn．1000-1158．2014．06．03

2013-04-03；

2014-08-21

国家自然科学基金（60903084，61172134，61201300）；浙江省自然科学基金（LY13F030017）；浙江省科技计划项目（2014C33105）

席旭刚（1975－），男，杭州电子科技大学副教授，主要研究方向为生物医学信息检测、模式识别和机器人技术。xixugang＠hdu.edu.cn