基于NSST和自适应PCNN的图像融合算法
2014-06-07江平,张强,李静,张锦
江 平,张 强,李 静,张 锦
(合肥工业大学数学学院,安徽合肥230009)
基于NSST和自适应PCNN的图像融合算法
江 平,张 强,李 静,张 锦
(合肥工业大学数学学院,安徽合肥230009)
针对红外和可见光图像的特点,本文提出了一种基于非下采样剪切波变换(NSST)和自适应的脉冲耦合神经网络(PCNN)相结合的红外与可见光图像融合的新算法。对经过NSST变换后的低频子带系数采用带高斯权重分布矩阵的局域方差和方差匹配度相结合的融合规则,对高频子带系数采用一种改进的空间频率作为PCNN输入,且采用改进的拉普拉斯能量和作为PCNN的链接强度,利用PCNN全局耦合性和脉冲同步性选择高频子带系数,最后经NSST逆变换后得到融合结果。实验结果表明,本文提出的算法与传统的图像融合算法相比不仅在主观视觉上取得较好的效果,而且在客观标准上也有了一定的提高。
图像融合;非下采样剪切波变换(NSST);脉冲耦合神经网络(PCNN);空间频率;拉普拉斯能量和
1 引 言
随着红外成像技术的飞速发展,红外与可见光图像融合成为图像处理领域的研究热点[1-2]。融合后的图像可以有效地综合红外图像目标特征和可见光图像中场景细节信息。小波变换具有良好的方向性和局部化特征可以较好地表示图像的细节信息,但小波变换在一维时的优良特性并不能简单地推广到二维或更高维。于是,多尺度几何分析受到广泛关注主要有Ridgelet、Curvelet、Contourlet、Shearlet等变换工具。Contourlet变换(CT)是由DO等人[3]提出,其与小波分析相比具有良好的多分辨率和方向性但缺乏平移不变性,为此Cunha等人[4]提出非下采样Contourlet变换(NSCT)。但是NSCT计算复杂度较高运行时间较长,Guo等人[5]提出了Shearlet变换(ST),ST与CT相比它没有方向数目和支撑基尺寸大小的限制且计算效率更高,并在图像融合中取得不错的效果[6]。然而由于ST不具备平移不变性,在图像融合时易在奇异点附近产生伪吉布斯现象。于是,Easley等人[7]提出了NSST,它具备剪切波的所有优点且有平移不变性。NSST在图像融合中的应用仍处于探索阶段,虽然曹等人[8]利用NSST进行图像融合,但是他们没有分析和讨论分解子图的融合规则,因此有必要进一步探究NSST在图像融合中的应用。
PCNN是Eckhorn等人[9]通过模拟猫的大脑视觉皮层中同步脉冲发放现象提出的模型,其具有全局耦合性和脉冲同步性,被广泛应用于图像融合[6,10-11]。Broussard等人[10]首先将PCNN应用于图像融合中,证实了PCNN用于图像融合的可行性。之后肖等人[11]提出了一种结合NSCT和PCNN的图像融合算法,但是由于他们没有考虑到链接强度β是个变量,因而融合效果不理想。综上,本文采用改进的拉普拉斯能量和作为PCNN的链接强度β,且采用改进的空间频率作为PCNN的输入。
2 基础知识
2.1 NSST理论[12]
当维数n=2时,具有合成膨胀的放射系统定义为:

式中,ψ∈L2(R2);A和B是2×2可逆矩阵;|det B|=1。如果MAB(ψ)具有如下形式的紧框架条件,则MAB(ψ)中的元素称为合成小波,即对∀f∈L2(R2),有:
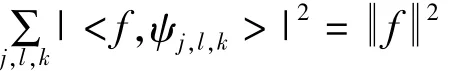
NSST离散化过程是由多尺度剖分和方向局部化构成:(1)多尺度剖分。通过非下采样金字塔组实现,图像经k级非下采样滤波器分解可以得到(k+1)个与原图像大小相同的子带图像,其中包括1个低频和k个高频子图;(2)方向局部化。NSST和ST不同,NSST的方向局部化是通过改进的剪切波滤波器实现,标准的剪切滤波器是在伪极化网格中通过窗函数的平移操作实现,执行过程中需要进行下采样操作,因而不具有平移不变性,而NSST把标准的剪切波滤波器从伪极化网格系统映射回到笛卡尔坐标系统,通过逆傅里叶变换,最后直接通过二维卷积就可完成其操作[7],因而避免了下采样操作而满足平移不变性。
2.2 PCNN理论
PCNN由多个神经元组成,每个神经元由三部分组成:接收域、调制域及脉冲产生器。
PCNN中图像每个像素点对应一个神经元,为了更好地将其应用于图像处理中,人们提出了各种改进模型。本文采用的是一种简化模型[2],其数学表达式如下:

式中,n是迭代次数;(i,j)表示剪切波系数在l尺度k方向的位置;(i,j)是神经元之间的链接权值矩阵;a,b是PCNN中链接范围大小;(i,j)和(i,j)分别是反馈输入和链接输入;Il,k(i,j)是外部输入刺激矩阵;(i,j)为内部活跃性总数;(i,j)为神经元间的链接强度;(i,j)为阈值;VL是链接输入放大系数;Vθ是阀值放大系数;αL和αθ分别为链接输入和变阀值函数的时间常数;(i,j)为PCNN的脉冲输出。如果Ul,k(i,j)>(i,j),则神经元产生一个脉冲Yl,k(i,j)=1,称为一次点火。
3 基于NSST与自适应PCNN的图像融合规则
假定待融合的红外图像(I)和可见光图像(V)已经过几何配准处理,图像融合流程如图1所示,融合步骤为:
(1)对I和V分别进行NSST分解,得到各自的图像分解后NSST系数:{CI}(l≥1)和{CV,}(l≥1)。其中,CI和CV为低频子带系数和ClV,k为l尺度下k方向上高频子带系数。
(2)对低频子带系数和各高频子带系数使用不同的融合策略,获得融合后的系数{CF,Cl,kF}(l≥1)其中,CF为融合后图像的低频子带系数;Cl,kF为融合后图像在l尺度下k方向上的高频子带系数。
(3)对融合后系数进行NSST逆变换,得到最终的融合图像F。

图1 红外和可见光图像融合流程图
3.1 低频子带系数融合规则
图像经过NSST变换后得到的低频部分代表了图像的近似分量,包含了源图像大量的能量信息。如果低频系数采用常规的融合算法,如加权平均法有可能丢失源图像中的一些重要信息或与源图像形成较大的灰度差异。图像的区域方差则反映了局部区域内图像信息量的丰富程度,因此本文采用局部区域方差匹配的融合规则对低频系数进行处理。
区域方差定义为:

式中,¯C为所选区域的灰度均值;CS(i,j)为红外(或可见光)图像低频子带系数在点(i,j)时的灰度值;G为以点P(k1,k2)为中心大小为M×N(本文取3× 3)的局部区域;w(i,j)是以点P为中心时矩阵各点的对应高斯权重分布系数,离点P越近权值越大,权值是通过行和列的高斯分布加权相加得到的。
局部区域的方差匹配度MS(k1,k2)定义为:
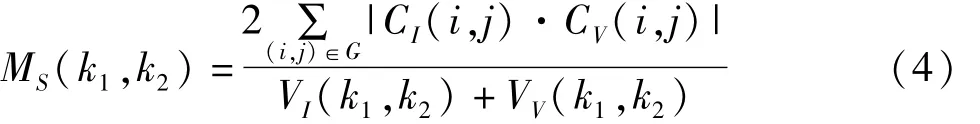
设α为方差匹配度阈值,本文取α=0.5。
当MS(k1,k2)<α时,表明两个区域的相关性差,区域方差大表示该区域包含更丰富的细节信息,因此采用方差取大的融合策略:

当MS(k1,k2)≥α时,表明两个区域的相关程度高,两个区域都包含相当的细节信息,因此采用加权平均融合策略:
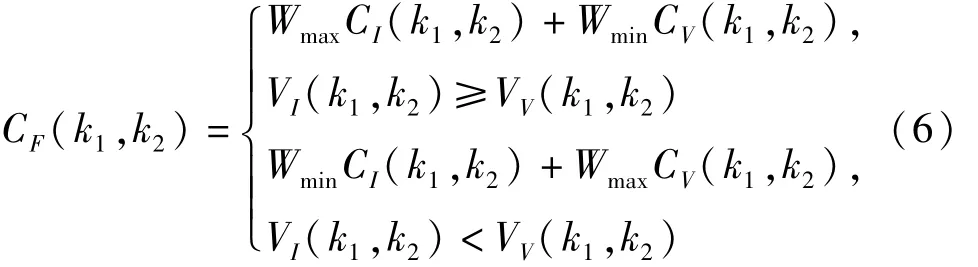
式中,Wmin和Wmax为定义的自适应因子且:

3.2 高频子带系数融合规则
3.2.1 改进的空间频率作为PCNN的刺激输入
由于NSST的高频子带系数代表了图像的细节分量,如边缘、直线、区域边界等。在文献[1]中,方勇等人首先成功地把PCNN应用到红外与可见光图像融合中,但他直接使用子带系数刺激PCNN,事实上人们对边缘等特征更加敏感。因此,单纯使用子带系数作为输入是不够的。图像的空间频率反映了一幅图像的总体活跃程度,空间频率越大图像越活跃、越清晰,因此在文献[13]中,屈等人使用空间频率作为PCNN的输入,取得了一定的效果。
对于M×N的矩阵,空间频率[13]定义为:

式中,RF表示行频率;CF表示列频率且:
由于式(7)中定义的空间频率只描述了水平和垂直信息而缺乏对角信息,这样就使得融合结果可能丢失很重要的细节信息。鉴于此,本文提出了一种改进的空间频率(MSF)。MSF包含了行频率(RF),列频率(CF),对角频率(DF1,DF2)。
对于M×N的矩阵,改进的空间频率定义为:
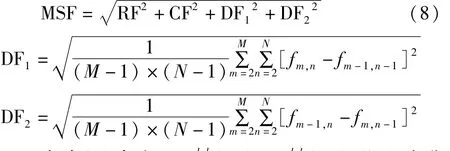
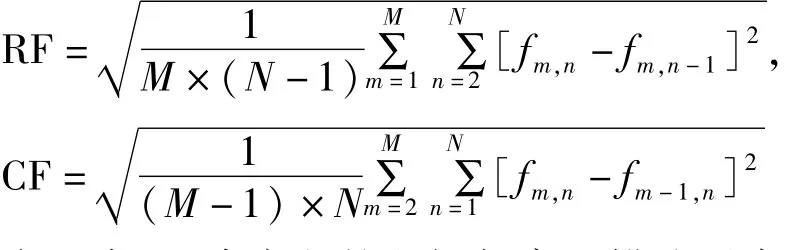
3.2.2 改进的拉普拉斯能量和作为链接强度β
在PCNN模型中的链接强度β表示当前神经元与其他神经元链接的强度,在图像中表现为当前像素值与其周围像素值的紧密联系。在传统的PCNN融合算法中,β取固定的常数。根据生理学和心理学研究发现,人眼对特征明显区域的反应要比不明显区域反应强烈,不可能每个神经元的链接强度都相同[14],而拉普拉斯能量和可以很好的反映图像的边缘特征信息,文献[15]利用拉普拉斯能量和进行图像融合取得了较好的效果。
拉普拉斯能量和[15]定义为:
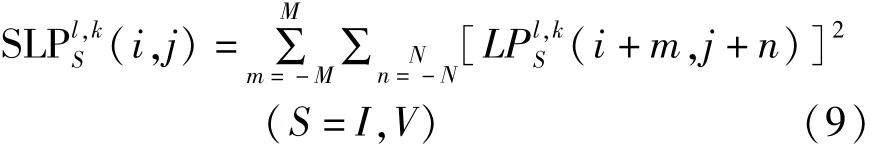
其中:
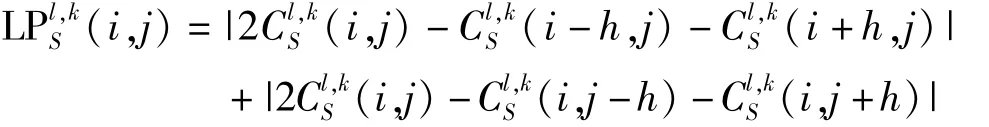
改进的拉普拉斯能量和定义为:
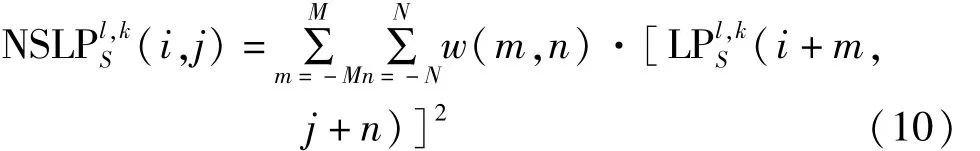
3.2.3 高频子带系数的判决选择
PCNN点火次数的大小反映了神经元所受到外部刺激的大小,表征了NSST变换中所含细节信息的多少,因此选取点火次数大的点所对应的NSST系数可得到更多源图像细节信息。选取步骤如下:
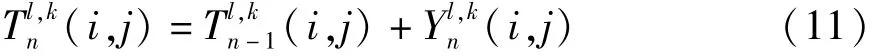
(2)当PCNN迭代到N时,由式(11)可以得到了一幅由Dl,k(i,j)表征的点火频率映射图:
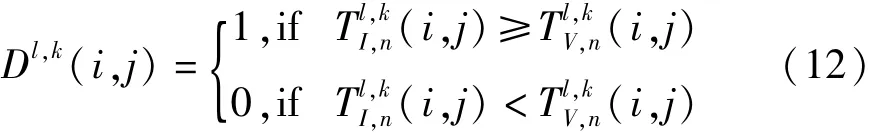
(3)根据式(12)选取点火次数大的点所对应的NSST系数作为最后融合图像的高频子带系数:
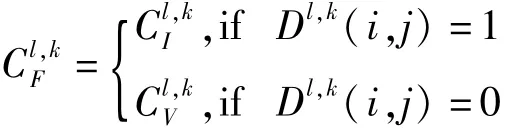
4 仿真实验及结果分析
本文采用严格配准的红外与可见光图像(大小均为256×256)进行仿真实验。将本文的算法与以下算法进行比较:基于梯度金字塔变换的融合算法(记为GP-mean-max)、基于离散小波变换融合算法(记为DWT-mean-max)、基于CT的融合算法(记为CT-mean-max)、基于ST的融合算法(记为ST-mean-max)、基于NSST的融合算法(记为NSST-mean-max),这些算法均采用低频子带系数取平均,高频子带系数取绝对值最大的融合规则;QU等人[13]提出的基于NSCT的融合算法(记为NSCT-mean-SFPCNN)和基于NSST的融合算法(记为NSST-mean-SFPCNN)融合规则均为低频子带取平均高频子带以空间频率为输入矩阵的PCNN。本文中PCNN的参数选取如下:N=200,αL=1.0,αθ=0.2,VL=1.0,Vθ=20,a×b=3×3 W=[0.707 1 0.707; 1 0 1; 0.707 1 0.707]。
为了定量评价融合效果,本文采用标准差、信息熵、互信息[17]和QAB/F[18]作为客观评价指标。标准差(STD)反映了灰度相对灰度均值的离散程度,标准差越大融合效果越好;信息熵(En)表示图像中所包含的平均信息量的多少;互信息(MI)是计算源图像有多少信息转移到融合后的图像中,互信息越大,说明该方法携带的信息量越大;QAB/F是衡量有多少边缘信息从源图像中转移到融合图像中,其值越大融合效果越好。
图2(a)为红外图像能够清晰看到一个欲穿过栅栏的人,但其他景物较模糊。图2(b)为同一场景的可见光图像,由于光线较暗,很难辨别可见光中的人,但栅栏、路、方桌、灌木丛等景物较清晰。图2(c)~图2(i)是本文选取的经典融合算法融合图像,图2(j)是本文算法的融合图像。从主观评价看,基于梯度金字塔的融合图像对比度比较低,图像较模糊;基于小波的融合效果虽有些改善但仍存在明显的波纹干扰;基于CT及ST,融合效果有一定的提高,但有明显的Gibbs块状效应,容易产生虚影模糊;至于NSST-mean-max、NSST-mean-SFPCNN这两种算法虽然使用了NSST变换但是由于融合规则的不足,融合效果仍不是很理想。而本文融合算法由于NSST具有方向敏感性等优良特性,可以提供不同的边缘和细节信息,再加上提出的融合规则可以在一定程度上改善其清晰度、对比度,细节信息相对更丰富,人的目标更清晰突出,有利于目标的识别与检测。

图2 源图像与融合结果图

表1 融合结果的客观评价数据
从客观评价看,表1给出了不同融合算法融合后的标准差、信息熵、互信息及QAB/F值,由表中可以看出本文提出算法的客观数据都高于其他算法,其结果基本与视觉特性保持一致。
5 结束语
本文提出了一种新的基于NSST和自适应PCNN的图像融合算法。NSST作为一种新的多尺度几何分析工具,可以多尺度多方向地描述图像,其执行过程更高效。为了更有效地利用PCNN的优良特性,本文采用改进的拉普拉斯能量和作为PCNN的链接强度和改进的空间频率作为PCNN的输入。实验结果表明,本文算法可以有效地综合红外图像的目标特征信息和可见光图像的场景细节信息,证实了本文算法是一种有效的融合算法。
[1] Fang Y,Liu SP.Infrared image fusion algorithm based on contourlet transform and improved pulse coupled neural networks[J].China Patent1873693A,December 2006.
[2] Li Meili,Li Yanjun,Wang Hongmei,et al.Fusion algorithm of infrared and visible images based on NSCT and PCNN[J].Opto-Electronic Engineering,2010,37(6):90-95.(in Chinese)李美丽,李言俊,王红梅,等.基于NSCT和PCNN的红外和可见光图像融合方法[J].光电工程,2010,37(6):90-95.
[3] Do M N,VetterliM.The contourlet transform:an efficient directionalmultiresolution image representation[J].IEEE Transactions on Image Processing,1992,40(4):882-893.
[4] Cunha A L,Zhou JP,DO M N.The nonsubsampled cont-ourlet transform:theory design and application[J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[5] Guo K,Labate D.Optimally sparsemultidimensional representation using shearlets[J].SIAM Journal on Mathematical Analysis,2007,39(1):298-318.
[6] Wang ZH,Wang JQ,Zhao DG,etal.Image fusion based on shearlet and improved PCNN[J].Laser&Infrared,2012,42(2):213-216.(in Chinese)王朝晖,王佳琪,赵德功,等.基于Shearlet与改进PCNN的图像融合[J].激光与红外,2012,42(2):213-216.
[7] Easley G,Labate D,Lim W Q.Sparse directional image representation using discrete shearlet transform[J].Applied and Computation Harmonic Analysis,2008,25(1):25-46.
[8] Cao Y,Li ST.Multifocus image fusion by nonsubsampled shearlet transform[C]//Proc.IEEE 6thInt.Conf.on Image and Graphics,IEEE Press,Piscataway,NJ,2011,17-21.
[9] Eckhorn R,Reiboeck H J,Arndt M,et al.Feature linking via synchronization among distributed assemblies:simulation of results from cat cortex[J].Neural Computation,1900,2:293-307.
[10]Broussard R P,Pogers S K,Oxley M E,et al.Physiologicallymotivated image fusion for object detection using a pulse coupled neural network[J].IEEE Transactions on Neural Networks,1999,10(3):554-563.
[11]XiaoW,Wang R F.Image fusion algorithm based on nonsubsampled contourlet transform and pulse coupled neural network.[J].Comput.Appl.,2008,28(S2):164-167.
[12]Jiao Licheng,Hou Biao,Wang Suang,et al.Image multiscale geometric analysis:theory and applications[M]. Xi’an:Xidian University Press,2008.(in Chinese)焦李成,候彪,王爽,等.图像多尺度几何分析理论与应用[M].西安:西安电子科技大学出版社,2008.
[13]Qu X B,Yan JW,Xiao H Z,et al.Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain[J].Acta Autom Sin.,2008,34(12):1508-1514.
[14]Wang Zhihui,Zhao Baojun,Shen Tingzhi.Image fusion based on MMPN and adjustable linking strength[J].Acta Electronica Sinica,2010,38(5):1162-1166.(in Chinese)王志慧,赵保军,沈庭芝.基于MMPN和可调节链接强度的图像融合[J].电子学报,2010,38(5):1162-1166.
[15]HuangW,Jing Z L.Evaluation of focusmeasures inmultifocus image fusion[J].Pattern Recognition Letters,2007,28(4):493-500.
[16]Hu Gang,Ji Xiaomin,Liu Zhe,et al.Regional feature selfadaptive image fusion method based on nonsubsampled steerable pyramid transform[J].Journal of Computer-Aided Design&Computer Graghics,2012,24(5):637-648.(in Chinese)胡钢,吉晓民,刘哲,等.结合区域特性和非下采样SPT的图像融合方法[J].计算机辅助设计与图像学报,2012,24(5):637-648.
[17]Qu G H,Zhang D L,Yan P F.Information measure for performance of image fusion[J].Electronics Letters,2002,38(7):313-315.
[18]Petrovic V,Xydeas C.On the effects of sensor noise in pixel-level image fusion performance[C].Proceedings Of the Third International Conference on Information Fusion,IEEE Press,2000,2:14-19.
Fusion algorithm for infrared and visible image based on NSST and adaptive PCNN
JIANG Ping,ZHANG Qiang,LIJing,ZHANG Jin
(School of Mathematics,Hefei University of Technology,Hefei230009,China)
Aiming at the feature of infrared and vision images,a new fusion algorithm which combines nonsubsampled shearlet transform(NSST)with adaptive pulse coupled neural network(PCNN)is presented.For the low-frequency sub-band coefficients,a fusion rule which combines local variance with a Gaussian weight distribution matrix after NSST transform with variancematching is used.For the high-frequency sub-band coefficients,an improved spatial frequency as the input of the PCNN is used,and the improved sum of Laplace energy as the PCNN link strength is used.The high-frequency sub-band coefficients are selected by using the global coupling and pulse synchronization of PCNN,and finally fusion results are obtained by inverse NSST transform.The experiment results show that compared to the traditional image fusion algorithms,the proposed algorithm achieves better results in the subjective visual and also improves the objective criteria in some extent.
image fusion;nonsubsampled shearlet transform(NSST);pulse coupled neural network(PCNN);spatial frequency;the sum of Laplace energy
TP391
A
10.3969/j.issn.1001-5078.2014.01.024
1001-5078(2014)01-0108-06
江 平(1972-),女,副教授,博士,研究方向为应用数值逼近,几何造型,图形图像处理等。E-mail:jiangping_72@sina.com
2013-04-27;
2013-06-27
