基于多维贪婪搜索的人工蜂群算法
2014-06-07张素琪滕建辅顾军华
张素琪,滕建辅,顾军华
(1.天津大学电子信息工程学院,天津300072;2.河北工业大学计算机科学与软件学院,天津300401)
基于多维贪婪搜索的人工蜂群算法
张素琪1,滕建辅1,顾军华2
(1.天津大学电子信息工程学院,天津300072;2.河北工业大学计算机科学与软件学院,天津300401)
人工蜂群算法在多峰高维函数优化问题的求解上取得了较好的结果,但随着函数的复杂度及维数增高,仍存在收敛速度慢、易陷入局部最优等问题。为此,提出一种新的人工蜂群算法。将人工蜂群对食物源的单维贪婪搜索改进为多维贪婪搜索以增强蜂群的搜索能力,避免在个别维度上出现较优解的食物源由于达到更新阈值却被废弃而造成迂回搜索的现象,引入扰动搜索机制避免迭代后期食物源位置在个别维度收敛导致算法陷入局部最优。仿真实验结果表明,该算法能保持深度挖掘和广度搜索上的平衡,在高维函数优化问题求解的收敛速度和计算精度方面表现出较好的性能。
人工蜂群算法;函数优化;贪婪搜索;扰动搜索;深度挖掘;广度搜索
1 概述
文献[1]提出了人工蜂群(Artificial Bee Colony, ABC)算法。该算法是一种模仿蜂群觅食行为的优化方法,其控制参数少,简单易操作,在高维函数优化问题求解方面与遗传算法、粒子群算法、和声算法以及差分进化算法相比表现出良好的特性[2-4],已成为国内外学者们关注的热点。文献[5]提出了CABC方法,通过构造混沌序列实现食物源的初始化,以改善各个食物源分布的均匀性和搜索的广泛性,在避免算法陷入局部最优方面取得了一定效果。文献[6-7]引入了混沌的概念,在算法迭代一定次数后,在缩小的新区域上通过混沌搜索初始化一部分新的食物源,以提高搜索的多样性。文献[8]应用反向学习理论来初始化食物源,同样使食物源的多样性得到增强。一些学者通过将标准ABC中观察蜂的轮盘赌选择改为boltzmann选择和轮盘赌反向选择来保持食物源的多样性,避免算法过早收敛[9-10]。文献[11-13]将个体最优和全局最优加入工蜂和观察蜂的搜索策略中以加快算法的收敛。文献[14-15]借鉴差分进化算法的变异策略来改进蜂群的搜索策略。本文提出一种多维贪婪搜索,使工蜂和观察蜂均具备多维搜索的能力,以提升算法的搜索能力和收敛速度。
2 函数优化问题的求解
在ABC算法中,蜂群以获得更好的食物源为目的,不断更新食物源的位置信息。人工蜂群包含3种蜜蜂:工蜂,观察蜂和侦查蜂,3种蜜蜂互相配合,共同更新食物源的位置。ABC算法在解决函数优化问题时,每个食物源的位置都代表优化问题的一个可行解,可行解在蜂群进行一次工作后得到更新,不断迭代后,可行解集中出现最优解,问题得以解决。下面说明ABC算法解决函数优化问题的几个重要步骤。
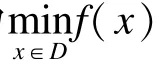
Step 1 初始化n个食物源的位置:
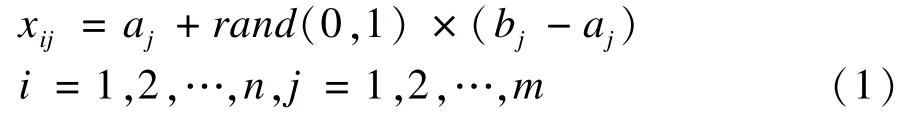
Step 2 每个工蜂在所属食物源xi附近进行搜索,选择候选食物源x′i,如果f(x′i)<f(xi),那么当前的食物源由候选食物源x′i替换,即xi←x′i,同时limit(i)置为0,否则食物源保持不变且limit(i)增加1,称为贪婪搜索或贪婪修正,修正公式如下:
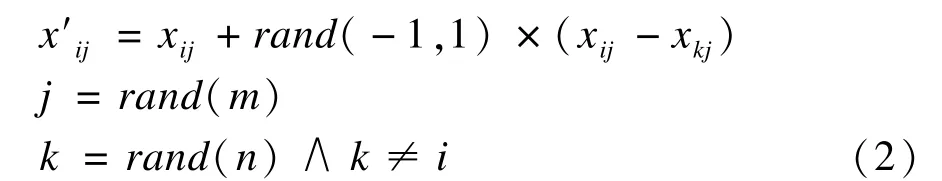
显见,候选食物源的每次选择本质上是在求解空间中随机选择一个维度进行修正,称为单维贪婪搜索。
Step 3 每一个工蜂完成对应食物源的修正后,观察蜂根据所有工蜂所代表食物源的质量,按照式(3)计算概率进行轮盘赌选择,确定观察蜂要选择的食物源,可表示为s=roulette(n)。

观察蜂在选定食物源xs的附近按照式(2)进行搜索并修正食物源位置,同时更新limit(s)。
Step 4 判断每个食物源的更新记录,如果limit(i)≥N_limit,该食物源废弃,侦查蜂将按照式(1)随机生成新的食物源。这样,ABC算法的一次迭代完成。
容易发现ABC算法中工蜂和观察蜂搜索新食物源的策略相同但是对食物源的选择方式不同。每个工蜂在所属食物源xi附近都会进行新的食物源搜索,如果找到更优的食物源,修正食物源的同时其对应limit(i)将会置为0,若没有得到更新,食物源limit(i)将会增加1。而观察蜂则根据轮盘赌选择食物源,并在该食物源附近进行新的食物源搜索。这样,质量较差的食物源得到更新的机会较少,而质量较优的食物源可能会被多次选择,有更多的更新机会。
通过观察ABC算法对多维函数的求解,发现当函数维度不断增加时,ABC的单维贪婪搜索显得越发不够,求解过程中在个别维度上出现较优解而没有得到继续挖掘的解由于达到N_limit次的限制而被废弃,之后由侦查蜂重新随机搜索,导致ABC错过很多达到全局最优的机会而需要在其他食物源上重新开始,增加了收敛时间,同时也影响了最终求解的精度。鉴于此,本文提出了基于多维贪婪搜索的ABC算法。
3 多维贪婪搜索ABC算法
3.1 多维贪婪搜索
每一种群体智能优化算法都必须具备广度探索和深度挖掘的能力,广度探索指在整个搜索空间中探索未知域以发现全局最优,而深度挖掘是在前一个较好解的基础上继续挖掘更优解的过程。只有广度探索和深度挖掘互相配合,达到平衡,才能使得优化算法在不断求解中得到全局最优。文献[10-15]在标准ABC算法的基础上均对搜索策略做了一些改进,但这些改进在增大搜索能力的同时,也破坏了标准ABC算法在广度探索和深度挖掘上的平衡,而需要改变种群初始化方法、观察蜂的选择方法或侦查蜂的搜索方法来增加种群的多样化,使算法重新达到平衡,势必增加时间消耗。本文提出的新算法在增大搜索力度的同时,并没有破坏广度和深度上的平衡,称为基于多维贪婪搜索的人工蜂群算法(multidimensional ABC,mdABC)。mdABC针对工蜂和观察蜂在搜索新食物源的过程中,进行每一维度的修正尝试后都进行贪婪选择,如果当前维度的尝试成功就保留该维度的修正,而在此基础上进行下一维度的尝试,如果失败就将该维度上的值退回原值后进行下一维度的探索,因此称为多维贪婪搜索。设当前工蜂或观察蜂所在的食物源为xi=(xi1, xi2,…,xij,…,xim),在食物源 xi附近搜索新食物源x′i=(x′i1,x′i2,…,x′ij,…,x′im)的具体步骤如下:
首先初始化更新标志位为sign=0,针对食物源的每一维xij(j=1,2,…,m)做如下操作:
(1)随机选择当前食物源附近的第k个食物源来计算x′ij:
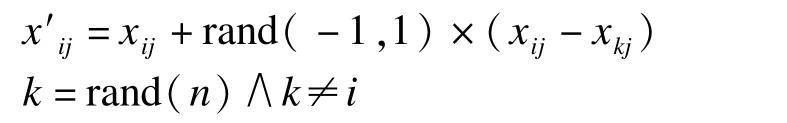
(2)如果x′ij超出该维度上的限定[aj,bj],则进行调整:
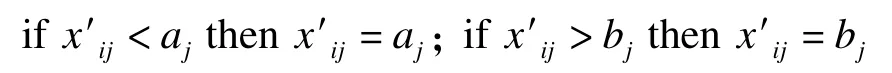
(3)判断x′ij是否能使得相应的f(x′)得到改善,如果得到改善则保留x′ij并更新标志位,否则返回原值xij:
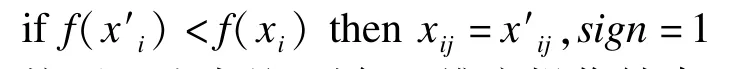
按照上述步骤,对每一维度操作结束后,进行标志位判断,如果标志位为1,说明在m维的探索中,有至少一维探索成功并进行了修正,如果标志位为0,说明探索失败,未做修正。
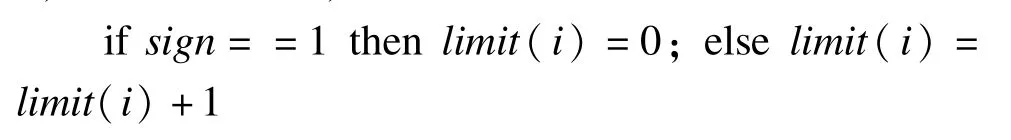
3.2 扰动搜索
通过实验分析,发现在食物源经过工蜂、观察蜂和侦查蜂的多次迭代修正后,最后食物源的位置在个别维度上逐渐趋于一致,设在维度 j上有 xijxkj=0,则按照式(2)将导致食物源在该维度上无法得到修正,因此,按照式(4)增加一个扰动机制,以避免该维度上的搜索停滞,避免陷入局部最优。
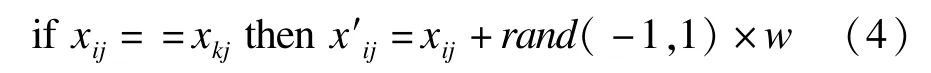
其中,w是一个扰动参数,通常取0.01,也可以根据不同的函数和临域范围进行设置。
3.3 mdABC的基本流程
下面给出mdABC的伪代码,其中3行~14行和15行~27行详细描述了工蜂和观察蜂的多维贪婪搜索过程。扰动搜索机制应用在第 8行和第21行。常量Max_iter为算法的迭代次数;n为食物源的个数,工蜂、观察蜂和侦查蜂数量分别为n,n,1; m为目标函数的维数;N_limit为食物源更新阈值;变量sign为更新标志位;limit记录每个食物源未得到更新的次数,max_limit为其中最大值。


4 数值仿真实验和结果分析
为了验证mdABC的有效性,在Matlab2010a平台上进行仿真,实验设备为内存 8 GB、处理器3.4 GHz以及64位Win7系统。采用了常用的4个标准函数[1-4]:Sphere函数,Rosenbrock函数,Ratrigin函数和Griewank函数,如表1所示。其中,Sphere和Rosenbrock为单峰函数;Ratrigin和Griewank为多峰函数;Rosenbrock是一个复杂的单峰函数,其全局最小值位于一个平滑的、弯曲路径上的谷底,一般情况下很难获得最优解;Griewank是一个复杂的多峰函数,其局部极小值点会随着维度的增大而增多,当维度大于等于30之后,多极值点消失成为单峰函数,相对于低维变得简单。测试主要针对mdABC、ABC算法进行求解精度和收敛速度的比较。参数设置与文献[4]相同:食物源个数为 20,迭代次数均为2 500,控制参数N_limit对所有函数均设置为100。
对每个测试函数分别取维度为5,10,30,50,100,算法独立运行10次,记录10次的均值、平均差和求取到最优值的平均迭代次数,实验结果如表2所示,其中,M表示平均值;S表示平均差;I表示平均迭代次数。

表1 标准测试函数
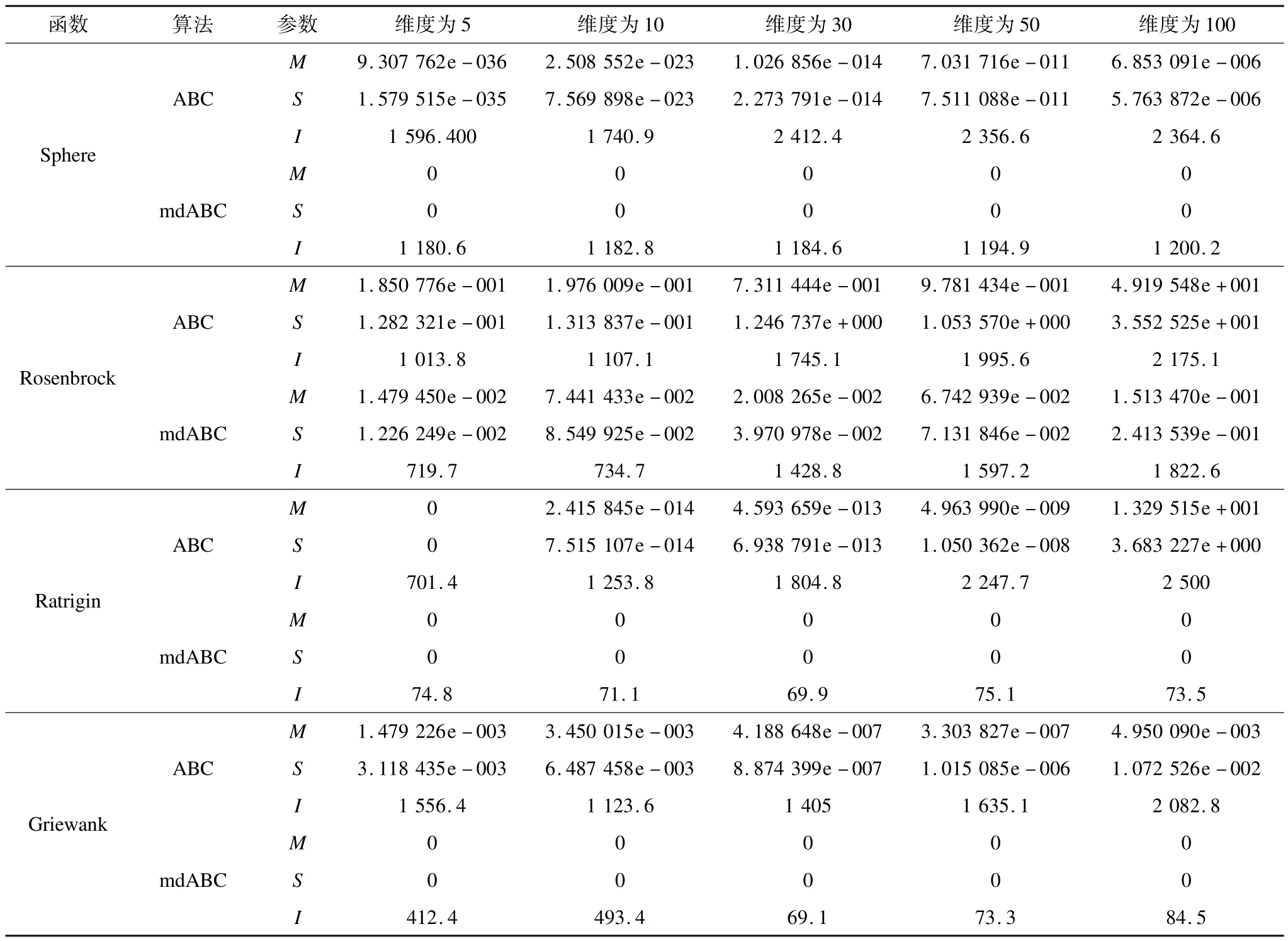
表2 mdABC与ABC算法的性能比较
图1中的曲线分别描述上述参数设置下函数1~4(维度为30)的迭代过程。
由图1和表2可看出,对于单峰函数Sphere和多峰函数Ratrigin,Griewank,mdABC的收敛速度和求解精度较标准ABC算法有明显的改善;特别是对于单峰Sphere和多峰Ratrigin函数,在不同维度设置下,均分别在迭代到1 200次和80次时已求得最优值0(Matlab2010a中将小于1e-324的数处理为0),而且多次运行的均值和标准差均为0。对于复杂的 Rosenbrock函数,在低维情况下mdABC的优势相对较弱,但随着维数的升高,优势变得逐渐明显。
对于Griewank函数,在维度低于30时为复杂多峰函数,mdABC在迭代到500次时已求得最优值0,在维度等于和高于30变为单峰函数时,在迭代到80次左右就已求得最优值0。综上,mdABC算法相对于标准ABC算法在收敛速度和求解精度上都得到了很大程度的改善。
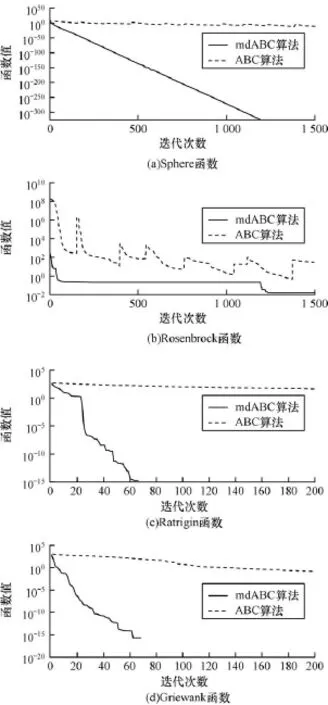
图1 函数迭代曲线
5 结束语
针对ABC算法在高维函数优化问题上收敛速度慢、易陷入局部最优的问题,本文提出了包含扰动机制的多维贪婪搜索mdABC算法。实验结果表明,该算法在求解精度和收敛速度上都优于标准ABC算法,在保持深度挖掘和广度搜索上的平衡方面表现出良好的性能。本文仅针对ABC算法的搜索机制进行了研究,在此基础上对种群初始化方法、观察蜂确定食物源方法的研究将是下一步工作的重点。
[1] Karaboga D.An Idea Based on Honey Bee Swarm for Numerical Optimization[R].Kayseri,Turkey:Erciyes University,Technical Report:TR06,2005.
[2] Karaboga D,Basluzk B.A Powerfuland Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony(ABC)Algorithm[J].Journal of Global Optimization,2007,39(3):459-471.
[3] Karaboga D,Basluzk B.On the Performance of Artificial Bee Colony(ABC) Algorithm[J].AppliedSoft Computing,2008,8(1):687-697.
[4] Karaboga D,Akay B.Artificial Bee Colony(ABC), Harmony Search and Bees Algorithms on Numerical Optimization[C]//Proceedings of Innovative Production Machines and Systems Virtual Conference.Melikgazi, Turkey:[s.n.],2009.
[5] Alatas B.Chaotic Bee Colony Algorithms for Global Numerical Optimization[J].ExpertSystemswith Applications,2010,37(8):5682-5687.
[6] 罗 钧,李 研.具有混沌搜索策略的蜂群优化算法[J].控制与决策,2010,25(12):1913-1916.
[7] 暴 励,曾建潮.自适应搜索空间的混沌蜂群算法[J].计算机应用研究,2010,27(4):1330-1334.
[8] Gao Weifeng,Liu Sanyang.A Modified Artificial Bee Colony Algorithm [J].Computers & Operations Research,2012,39(3):687-697.
[9] 丁海军,冯庆娴.基于Boltzmann选择策略的人工蜂群算法[J].计算机工程与应用,2009,45(31):53-55.
[10] 向万里,马寿峰.基于轮盘赌反向选择机制的蜂群优化算法[J].计算机应用研究,2013,30(1):86-89.
[11] Zhu Guopu,Kwong S.Gbest-guided ArtificialBee Colony Algorithm for Numerical Function Optimization[J].Applied Mathematics and Computation,2010,217 (7):3166-3173.
[12] Banhaznsakun A,AchalakulT,SizinaovakulB.The Best-so-Far Selection in Artificial Bee Colony Algorithm[J].Applied Soft Computing,2011,11(2):2888-2901.
[13] 王慧颖,刘建军,王全洲.改进的人工蜂群算法在函数优化问题中的应用[J].计算机工程与应用,2011,47 (13):36-39.
[14] Gao W F,Liu S Y.Improved Artificial Bee Colony Algorithm for Global Optimization[J].Information Processing Letters,2011,111(17):871-882.
[15] 向万里,马寿峰.基于向量整体扰动的快速收敛人工蜂群算法[J].计算机应用研究,2013,30(5): 1329-1333.
编辑 顾逸斐
Artificial Bee Colony Algorithm Based on Multi-dimensional Greedy Search
ZHANG Suqi1,TENG Jianfu1,GU Junhua2
(1.School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China;
2.School of Computer Science and Software,Hebei University of Technology,Tianjin 300401,China)
Artificial Bee Colony(ABC)algorithm can be efficiently employed to solve the multimodal and high dimensional function optimization problem.However,low search speed and premature convergence frequently appear with more complex problem.In order to improve the algorithm performance,this paper proposes a new artifciall bee colony algorithm.It introduces a search equation based on multi-dimensional greedy search to enhance local search and avoid the solution to be abandoned which achieves optimum value in some dimensions but reach the maximum update limit.New algorithm also adds a disturbance mechanism to avoid obtaining partial optimal solutions when premature convergence in a few dimensions.Experimental results show the new algorithm can balance the exploitation and exploration,has more fast convergence speed and better computational precision in solving the multimodal and high dimensional function optimization problem.
Artificial Bee Colony(ABC)algorithm;function optimization;greedy search;disturbance search;depth excavation;scope search
1000-3428(2014)11-0189-05
A
TP301.6
10.3969/j.issn.1000-3428.2014.11.037
天津市应用基础与前沿技术研究计划基金资助重点项目(13JCZDJC26300)。
张素琪(1980-),女,博士研究生,主研方向:信号处理,数据挖掘;滕建辅、顾军华,教授、博士。
2013-12-02
2013-12-31E-mail:suqizhang80@163.com
中文引用格式:张素琪,滕建辅,顾军华.基于多维贪婪搜索的人工蜂群算法[J].计算机工程,2014,40(11):189-193.
英文引用格式:Zhang Suqi,Teng Jianfu,Gu Junhua.Artificial Bee Colony Algorithm Based on Multi-dimensional Greedy Search[J].Computer Engineering,2014,40(11):189-193.
