基于FPGA的调制波周期归一化PWM研究

江 超,胡越黎

(上海大学机电工程与自动化学院,上海200072)

基于FPGA的调制波周期归一化PWM研究

江 超,胡越黎

(上海大学机电工程与自动化学院,上海200072)

研究调制波周期归一化脉冲宽度调制(PWM),把数字系统中用于记录存储数据Ram的地址Address与PWM脉冲宽度相互映射,给出一般性结论。基于这一模型结构,设计调制波周期归一化PWM的现场可编程门阵列数字系统。针对设计该数字系统时出现的包括模拟量数字化、调制比M、载波比N以及调制波周期归一化PWM各环节具体数字化实现等问题予以分析并解决。对周期脉冲值Pn进行简单设置,便可快速实现调制波周期归一化PWM模型结构的波形输出。

调制波周期归一化;脉冲宽度调制;调制比;载波比;现场可编程门阵列

1 概述

脉冲宽度调制(Pulse Width Modulation,PWM)源于通信调制技术。文献[1]把通讯调制技术应用到交流传动中,产生了正弦脉冲宽度调制(Sinusoidal PWM)变频变压思想,即用一组等腰三角形波与一个正弦波比较,其交点作为开关管“开”或“关”时刻[2-3];基于开关管响应速度原因,文献[4-5]把PWM正式应用于交流传动中,调制技术由此得到推广和发展[6-7]。

冲量等效原理认为惯性系统被不同脉冲作用时,如果其冲量对时间积分相等,即可以认为其作用效果基本相等[8]。冲量是指脉冲面积,效果基本相同是指输出响应波形基本相同,这便是PWM理论基础。通过对一系列脉冲的宽度进行调制,可以等效地获得所需波形[9-10]。

目前常用PWM技术有等面积法、自然采样法、规则采样法、不规则采样法、低次谐波消去法等[11-12]。本文立足等面积法和自然采样法,阐述一种基于调制波周期归一化PWM波形产生的新模型结构,并在FPGA上实现。介绍调制波周期归一化PWM数字系统中归一化地址Address与PWM脉冲宽度之间映射关系;针对数字系统中硬件资源有限性,分析PWM频谱特性,合理筛选调制比M、载波比N(调制比M为调制信号与载波信号幅值之比,载波比N为载波信号与调制信号频率之比);基于FPGA平台,设计基于调制波周期归一化PWM这一模型结构的PWM波形产生系统,通过对其M,N和调制波周期归一化PWM周期脉冲值Pn进行设置,实现输出PWM脉冲波。

2 调制波周期归一化PWM

调制信号和载波信号为PWM波形产生系统中2个基本要素。数字系统中,常用数据存储器Ram来存储这2种信号,其中,每一个地址Address(A)对应一个数据Data(D)。

如图1所示,3列波形为正弦调制波Sin,三角载波Carrier和基于调制波周期归一化PWM,横坐标A和Pn对应于时间参数t。当 Carrier大于 Sin时PWM输出为高即“开”,当Carrier小于Sin时PWM输出为低即“关”。

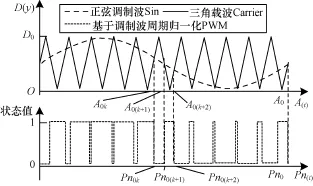
图1 调制波周期归一化PWM基本原理

本文巧妙地把数字系统中用于存储调制信号

Sin的Ram地址Address(A)与PWM脉冲宽度起始和截止时刻进行映射,如A0k-Pn0k,A0(k+1)-Pn0(k+1)和A0(k+2)-Pn0(k+2);A0为 Sin中地址最大值,即代表着一个周期,Pn0为调制波周期归一化PWM周期脉冲值,即表示PWM脉冲序列一个周期。下面从时间域角度出发对其进行分析。

在数字系统中,Carrier与Sin联立方程组的解析值映射为存储着Sin的Ram地址Address(A)。当M=Mx,N=Nx,取Sin与Carrier交点映射地址Address(A)为Ax={Ax1,Ax2,…,Axk,Ax(k+1),Ax(k+2),…,Ax(2Nx-1),Ax(2Nx)}。对任一调制波周期归一化PWM周期脉冲值Pnx={Pnx1,…,Pnxk,Pnx(k+1),Pnx(k+2),…,Pnx(2Nx-1),Pnx(2Nx)},如式(2)所示。

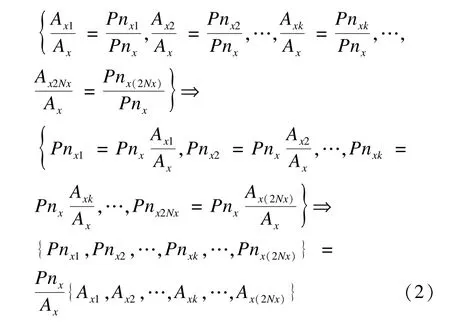
由式(2)可得Axk与Pnxk的对应关系。即不同M与N,解析出不同的Ax,针对任一Pnx,只需按照式(2)的映射关系便可求出相应PWM脉冲宽度的起始和截止时刻。以上分析虽然是以双极性PWM为基础,也同样适用于单极性PWM(双极性PWM采用正负交变三角载波Carrier与调制波Sin;单极性PWM采用180°三角载波Carrier与调制波Sin,与双极性相比,在一个周期的2个180°范围内,其三角载波极性相反,如图2所示)。

图2(a)、图2(b)为存储着载波信号Carrier和调制波信号Sin的2个Ram;图2(c)、图2(d)为由不同Ram地址发生器获得的双极性和单极性载波信号;图2(e)、图2(f)为双极性PWM和单极性PWM2列基准波形。结合式(2),由图 2(e)、图2(f)的比较结果,便可以输出调制波周期归一化PWM波形。

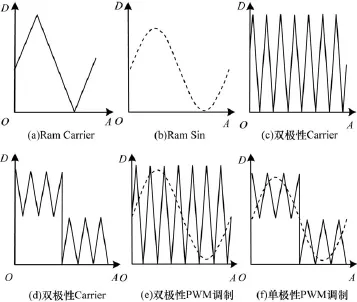
图2 双极性PWM与单极性PWM

3 调制波周期归一化PWM的FPGA实现

在数字系统中,鉴于硬件资源局限,不能无限扩大数据位数以追求其精度,通常以不影响数据运算分辨率为宜。在PWM数字系统中,调制信号Sin与载波信号Carrier联立方程组解析运算实际是用一系列阶梯波来代替,如图3所示。当描述Sin和Carrier数字位数不够多时,其交点就会出现遗漏或虚假,如图4数据507,数据373所示。

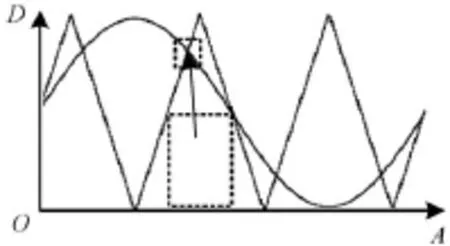
图3 数字系统中正弦调制波与三角载波波形

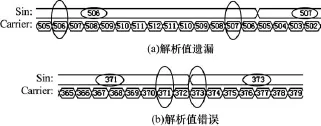
图4 数字系统中正弦调制波与三角载波解析

经计算,在PWM调制中,取载波比N=31,调制比M=1时,Sin与Carrier所有交点中相距最近的2个点横坐标差值约占一个Sin周期的万分之三,当Sin以13位数字量描述时,其精度可达万分之一点三,可避免上述情况发生。本文针对Sin和Carrier设计了2块13bit×13bit存储区域,如图5所示。

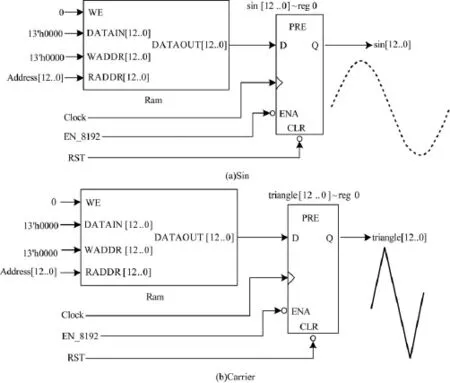
图5 Sin与Carrier存储区域

3.1 调制比M与载波比N

不同调制比M与载波比N,Sin与Carrier交点不同,输出PWM也不同,下面从双极性与单极性PWM频谱特性［13-14］分析M和N取值情况。

如图6双极性与单极性PWM频谱特性(M,N)所示,图6(a)为某一载波比(取N=11)下双极性与单极性PWM频谱中基波功率P曲线图。图6(b)为某一调制比(取M=0.95)下单极性与双极性PWM频谱中基波功率谱P的曲线图。

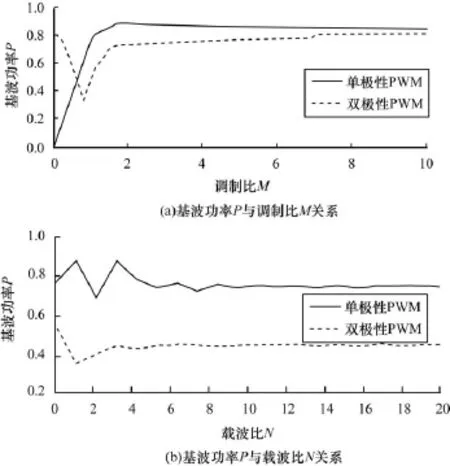
图6 双极性与单极性PWM频谱特性

在图6(a)中,双极性PWM中P呈现先下降后上升趋势,是因为当M较小时,其P值反映双极性三角载波信息,当M增大到一定值时,则主要反映调制波信息;单极性PWM中,P并没有呈现出先下降后上升的趋势,是因为单极性三角载波并没有像双极性三角载波那样对调制信息造成了较大干扰,使得P主要反映出调制波信息。在一定M范围内,其P随M线性变化,且其线性度好于双极性PWM情况。

在图6(b)中,在一定N范围内,其P基本不变,且在同样M与N下,单极性PWM的P值高于双极性PWM的情况。

综上:在N一定范围内,N的变化对基波功率谱P的影响较小(其主要引入载波谐波叠加干扰);随着M增加(双极性PWM中P呈现先下降后上升趋势;单极性PWM一定范围内有很好的单调性),P基本呈线性变化,在大于某些M处出现拐点,以使斜率下降,最后趋向于恒定值。基于以上分析,本文在设计PWM数字系统时便可合理设置M与N值。

3.2 PWM控制器

基于调制波周期归一化的PWM控制器系统结构［15-16］如图7所示。

图7 基于调制波周期归一化PWM控制器结构图

该系统结构包括:(1)I/O;(2)PWM模式寄存器组PWM_R;(3)分频地址计数器Carrier_N;(4)调制波与载波数据存储单元Sin_Ram(13bit×13bit)和Carrier_Ram(13bit×13bit);(5)调制比移位加法器Modulation_M;(6)调制波与载波归一化地址输出器Normalization_add;(7)归一化地址选择加法器Normalization_Mux_add;(8)归一化脉宽调制波形输出缓存器Normalization_buffer_shift_out。

I/O包括时钟信号Clk、复位信号Rst、使能信号PWM_EN、写寄存器使能 Wr_EN、寄存器地址Address［2:0］(这里的地址与本文提出的归一化地址不是一个概念)、寄存器数据输入Data_in、PWM输出PWM_outB［1:0］和PWM_outU［1:0］。

PWM模式寄存器组PWM_R有6个寄存器,如表1所示,分别为:双极性调制比与载波比寄存器MNB(Modulation_MB［2:0］=MNB［2:0］,Carrier_ NB［4:0］=MNB［7:3］),单极性调制比和载波比寄存器MNU(Modulation_MU［2:0］=MNB［2:0］, Carrier_NU［4:0］=MNB［7:3］),16位双极性PWM周期脉冲值寄存器PWM_pusleB［15:0］={PWMBH［7:0］,PWMBL［7:0］},16位单极性PWM周期脉冲值寄存器PWM_pusleU［15:0］={PWMUH［7: 0］,PWMUL［7:0］}。

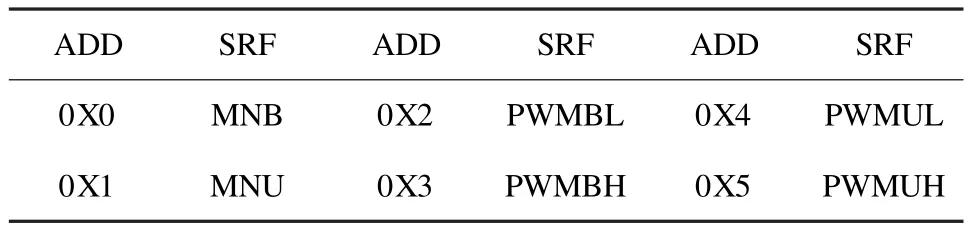
表1 PWM模式寄存器组PWM_R

由图7基于调制波周期归一化PWM控制器系统结构所示,通过I/O配置PWM_R;Carrier_N依据MNB和MNU载波比N(Carrier_NB［4:0］、Carrier_NU［4:0］)输出调制波与载波地址给Sin_Ram (13 bit×13 bit) 和 Carrier_ Ram (13 bit×13 bit)取出相应数据;Modulation_M依据MNB和 MNU中 Modulation_MB［2:0］和Modulation_MU［2:0］(M=0.8,0.85,0.9, 0.95,1.0,1.05,1.1,1.15)对Sin_Ram(13 bit× 13 bit)输出数据进行幅度调制;Normalization_ add对调制波和载波数据进行运算,以确定交点,同时得出归一化地址值及其个数;Normalization_ Mux_add依据归一化地址值及PWM_pusleB［15:0］={PWMBH［7:0］,PWMBL［7:0］},PWM_pusleU［15:0］={PWMUH［7:0］,PWMUL［7:0］}进行调制波周期归一化PWM数据计算,并把结果保存入Normalization_buffer_shift_out,其内部脉冲计数器通过与各归一化数据进行比较,确定输出状态为“0”或“1”以输出所需的归一化PWM脉冲宽度调制波形。

3.3 PWM主要功能模块

图7基于调制波周期归一化PWM控制器系统结构图 I/O,PWM_R,Carrier_N,Sin_Ram(13 bit× 13 bit)和Carrier_Ram(13 bit×13 bit)以及Modulation_ M的主要功能是做基本配置;Normalization_add, Normalization_Mux_add和Normalization_buffer_shift _out为调制波周期归一化PWM设计核心。

3.3.1 地址输出器

Normalization_add实现调制波与载波数据的比较以确定归一化地址值Nor_address,以及归一化地址个数。如图8调制波归一化地址、缓存数据仿真图所示。

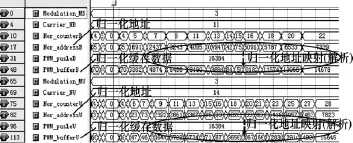
图8 调制波归一化地址、缓存数据仿真图

Carrier_NB［4:0］与 Modulation_MB［2:0］, Carrier_NU［4:0］与Modulation_MU［2:0］分别为双极性和单极性载波比N与调制比M;Nor_addressB［12:0］与Nor_addressU［12:0］为调制波与双极性(单极性)载波交点所对应的归一化地址值(即Sin_ Ram(13bit×13bit)存储单元中的地址信号),Nor_ counterB［5:0］与Nor_counterU［5:0］为归一化地址计数寄存器。

3.3.2 地址选择加法器

在图8中,PWM_pusleB［15:0］={PWMBH［7: 0］,PWMBL［7:0］},PWM_pusleU［15:0］= {PWMUH［7:0］,PWMUL［7:0］}为调制波周期归一化PWM周期脉冲值Pn,PWM_bufferB［15:0］, PWM_bufferU［15:0］为Pn对应的PWM脉冲归一化缓存数据,可用归一化地址选择加法器实现,如图9归一化地址映射解析框图所示。

图9 归一化地址映射解析框图

图中Clk、Rst和Ena为时钟信号、复位信号和使能信号;Nor_address［12:0］为归一化地址输入, PWM_pulse［15:0］为输入调制波周期归一化PWM周期脉冲值,PWM_buffer［15:0］为输出归一化缓存数据。Nor_address［12:0］各比特连接到数据选择器Mux的选择信号端,当该比特为“1”时选择输入PWM_pulse［15:0］相应高位作为Mux输出的低位,否则选择16′h0000;通过对各Mux输出进行加法运算可得PWM_buffer［15:0］。

3.3.3 脉宽调制波形输出缓存器

图10为归一化脉宽调制波形输出缓存器框图。针对归一化缓存数据进行保存、重新排序以及与脉冲计数器进行比较,以实现PWM波形输出。

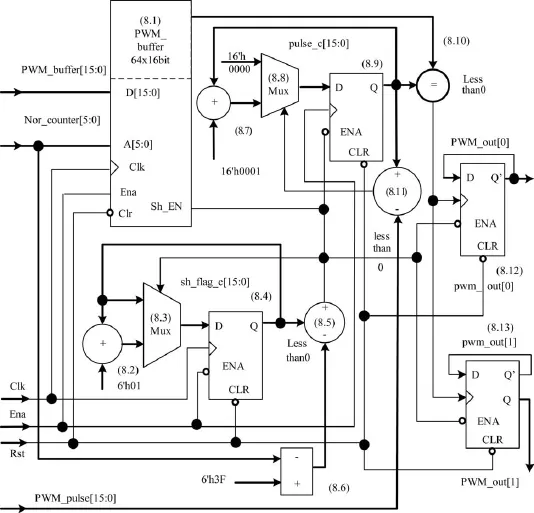
图10 归一化脉宽调制波形输出缓存器框图

归一化缓存数据PWM_buffer［15:0］与归一化地址计数寄存器Nor_counter［5:0］输入归一化移位缓存器PWM_buffer(64×16 bit)(8.1);计数器sh_ flag_c［15:0］(8.4)根据Nor_counter［5:0］与6'h3F比较结果及使能信号Ena实现对PWM_buffer(64× 16 bit)移位使能端Sh_EN以及脉冲计数器pulse_c［15:0］控制;pulse_c［15:0］(8.9)输出结果与PWM_buffer(64×16 bit)各存储值进行比较,用于驱动PWM输出缓存器PWM_out［1:0］,同时pulse_c［15:0］输出结果与输入信号PWM_pulse［15:0］进行比较实现计数器清零;寄存器 pwm_out［1:0］(8.12/13)连接PWM_out［0］,PWM_out［1］输出状态“0”或“1”,以输出所需的归一化PWM脉冲宽度调制波形。图11为FPGA中双极性、单极性PWM仿真波形图。

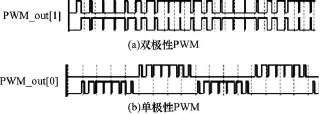
图11 FPGA中双极性、单极性PWM仿真波形图

4 系统验证与实验结果

为了实现基于 FPGA的调制波周期归一化PWM板级验证,搭建如图12所示的测试平台。

图12(a)中右边示波器为双极性PWM测试波形,如图12(b)所示;图中左边示波器为单极性PWM测试波形,这里对示波器的一端信号进行了反相,再结合其Math功能中的加法运算,便模拟出2列互补单极性PWM波的完整波形图,如图12(c)所示。

图12 FPGA板级测试验证

5 结束语

本文提出了一种基于调制波周期归一化PWM的波形产生方法。通过把数字系统中用于记录存储数据的地址(Address)与PWM脉冲宽度相互映射,得出归一化地址 Nor_address概念,设计了基于FPGA的调制波周期归一化PWM数字系统;并针对设计该系统时出现的包括模拟量数字化、调制比M和载波比N以及调制波周期归一化PWM各环节具体数字化实现等问题予以分析解决,只需简单地设置调制比M、载波比N和调制波周期归一化PWM周期脉冲值Pn,便可快速实现调制波周期归一化PWM波形输出。实验结果表明,基于调制波周期归一化PWM的FPGA系统操作方便,输出波形符合脉冲宽度调制要求,验证了此方法的有效性,具有一定的研究意义。

［1］ Schonung A,Stemmler H.Static Frequency Changers with Subharmonic Control in Conjunction with Reversible Variable Speed AC Drives［J］.Brown Boveri Rev.,1964,51(8/9):555-577.

［2］ Rashid M H.Power Electronics Handbook［M］.［S.l.］:Academic Press,2001.

［3］ Holmes D G,Lipo T A.Pulse Width Modulation for Power Converters［M］.［S.l.］:IEEE Press,2003: 95-152.

［4］ Bowes S R,Bird B M.Novel Approach to the Analysis and Synthesis of Modulation Processes in Power Converters［J］.IEEE Proceedings,1975,122(5): 507-513.

［5］ Bowes S R.New SinusoidalPulse-width Modulated Inverter［J］.IEEE Proceedings,1975,122(11): 1279-1285.

［6］ Bowes S R,Midoun A.New PWM Switching Strategy for Microprocessor-controller Inverter Drives［J］.IEEE Proceedings,1986,133(4):237-254.

［7］ Bowes S R,Holliday D.Optimal Regular-sampled PWM Inverter Control Techniques［J］.IEEE Transactions on Industrial Electronics,2007,54(3):1547-1559.

［8］ Khluabwannarat P,Thammarat C,Tadsuan S,et al.An Analysis of Iron Loss Supplied by Sinusoidal,Square Wave,BipolarPWM InverterandUnipolarPWM Inverter［C］//Proc.of Power Engineering Conference.［S.l.］:IEEE Press,2007:1185-1190.

［9］ 王立乔.正弦波逆变器脉宽调制技术的调制模型分析［J］.电力系统自动化,2008,32(7):45-49,99.

［10］ 李 涛,张晓锋,乔鸣忠.SPWM与SVPWM的宏观对等性研究［J］.中国电机工程学报,2010,30(s1): 178-184.

［11］ 郭 涛,孙玉坤,任明炜,等.链式多电平变换器特定谐波消除脉宽调制方法研究［J］.电力自动化设备, 2006,26(12):52-54,101.

［12］ 马丰民,吴正国,侯新国.基于统一PWM调制器的随机空间矢量调制［J］.中国电机工程学报,2007,27 (7):98-102.

［13］ 刘晓东,徐 弢.正弦脉宽调制技术开关时间点精度分析［J］.电力自动化设备,2010,30(12):55-59.

［14］ 伍家驹,王文婷,李学勇,等.单相SPWM逆变桥输出电压的谐波分析［J］.电力自动化设备,2008,28(4): 45-49,52.

［15］ Hu Yueli,Zhou Chen.Integration and Verification Case of IP-core Based System on Chip Design［J］.Journal of Shanghai University(English Edition),2010,14(5): 349-353.

［16］ 王 奔,仇乐兵,徐万良,等.基于FPGA的空间矢量脉冲宽度调制发生器设计［J］.电力自动化设备, 2012,32(2):56-61.

编辑 顾逸斐

Study of Modulation Waveform Cycle Normalization PWM Based on FPGA

JIANG Chao,HU Yueli
(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China)

A novel Pulse Width Modulation(PWM)waveform generating method based on modulation waveform cycle normalization is proposed.Mapping between address storing data in digital system and pulse width of PWM waveform is the key essence.According to it,a system based on Field Programmable Gate Array(FPGA)is designed and implemented,and difficulties like analog digitization,modulation ratio M,carrier ratio N and details for modulation waveform cycle normalization digitization are solved.With setting modulation waveform Pn for PWM,a specific PWM waveform based on modulation waveform cycle normalization can be achieved successfully,which shows the effectiveness of the method.

modulation waveform cycle normalization;Pulse Width Modulation(PWM);modulation ratio;carrier wave ratio;Field Programmable Gate Array(FPGA)

1000-3428(2014)11-0297-07

A

TP391

10.3969/j.issn.1000-3428.2014.11.059

国家自然科学基金资助项目“硅基有机发光微显示器的高性能顶发射界面及数字驱动研究”(61376028);上海市科委基金资助项目“高清硅基OLED微显示器件设计制造技术”(13111104600)。

江 超(1987-),男,硕士研究生,主研方向:汽车电子,PWM控制自动化,现场可编程门阵列;胡越黎,教授、博士、博士生导师。

2013-09-18

2013-11-11E-mail:shu_jcleehom@shu.edu.cn

中文引用格式:江 超,胡越黎.基于FPGA的调制波周期归一化PWM研究[J].计算机工程,2014,40(11):297-303.

英文引用格式:Jiang Chao,Hu Yueli.Study of Modulation Waveform Cycle Normalization PWM Based on FPGA[J].Computer Engineering,2014,40(11):297-303.